[Golang修仙之路] 算法专题：回溯（递归）

Announce：回溯这块我主要是跟着labuladong的算法笔记学习，他b站有视频讲解，也有自己的网站。

1. 递归的两种思维方式

1.1 思维方式一: 分解问题

把原问题分解为规模更小的子问题。这类思维方式的特点是：

• 递归函数往往有明确的含义。
• 递归函数往往有返回值。

1.1.1 例1

斐波那契数列。

递归函数的含义是：返回第N个斐波那契数列的值。

原问题是2个更小的子问题之和。

1.1.2 例2

二叉树的最大深度。

递归函数的含义是：以root为根节点的树的最大深度。

原问题是 MAX（左子树的最大深度，右子树的最大深度）+ 1

1.2 思维方式二: 遍历

这种思维方式，写出的递归函数往往没有返回值。

2. 回溯时间复杂度计算⭐️

递归函数本身的时间复杂度 * 递归函数调用次数

递归函数调用次数 = 多叉树节点个数（N！）

3. 回溯法解决：排列/组合/子集 问题

再次声明，这篇文章仅仅是个人学习笔记，原创来自：labladong

问题分类：

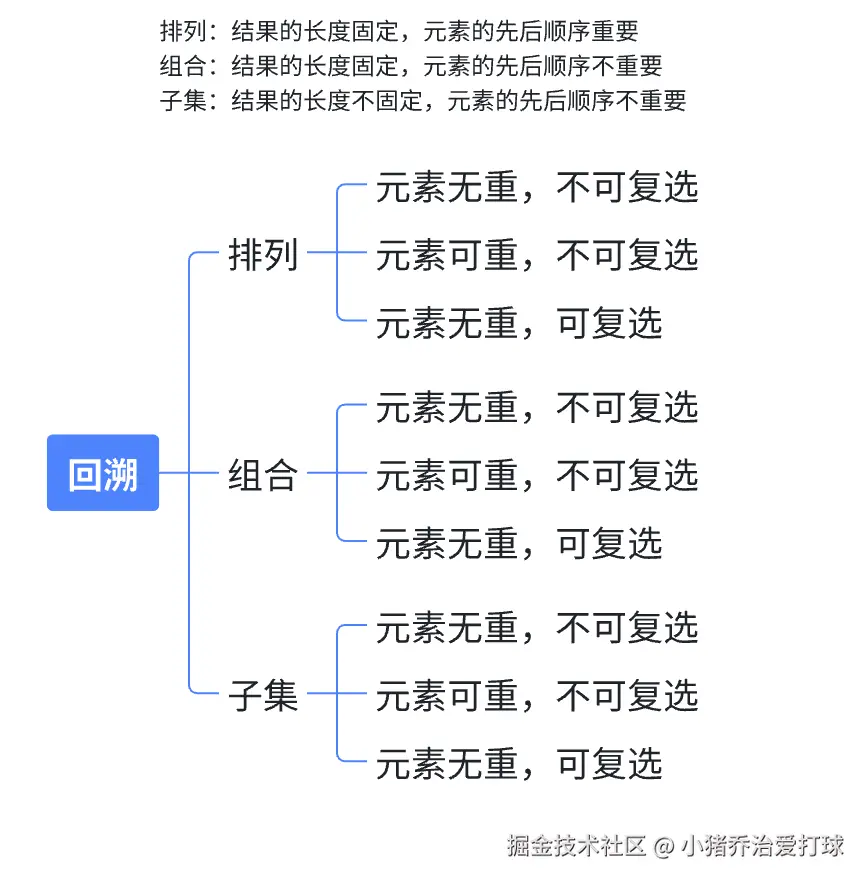
逐一解释，我说实话，不如直接通过例题来说明。

• 元素无重复：
  • 就是输入的数组应该是没有重复元素的，如[1,2,3]
  • 而不能是有重复元素的，如[1，1，2]
• 不可以复选：
  • 一个元素只能使用一次，不能无限使用。（有点像01背包和无穷背包那种概念）

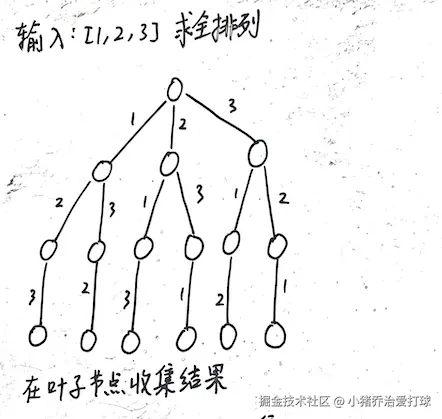
3.1 排列

3.1.1 什么是排列？

nums = [1,2,3]
[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

3.1.2 如何思考：排列树

排列树：

3.1.3 condition-1: 元素无重，不可复选

例题：LCR 083. 全排列

代码：

func permute(nums []int) (res [][]int) {
    n := len(nums)
    used := make([]bool, n)
    track := []int{}
    dfs(nums, track, used, &res)
    return
}

// used 是排列 + 无重复不可复选 问题独有的
func dfs(nums []int, track []int, used []bool, res *[][]int) {
    // 退出条件
    if len(track) == len(nums) {
        tmp := make([]int, len(track))
        copy(tmp, track)
        *res = append(*res, tmp)
        return
    }
    // for循环
    for i, _ := range nums {
        if used[i] {
            continue
        }
        // 往下"递"
        track = append(track, nums[i])
        used[i] = true
        dfs(nums, track, used, res)
        // 往上"归"
        track = track[:len(track)-1]
        used[i] = false
    }
}

3.1.4 condition-2: 元素可重，不可复选

核心：排序 + nums[i] == nums[i-1] && !used[i-1]

这张图真是哥们儿理解了之后自己画的。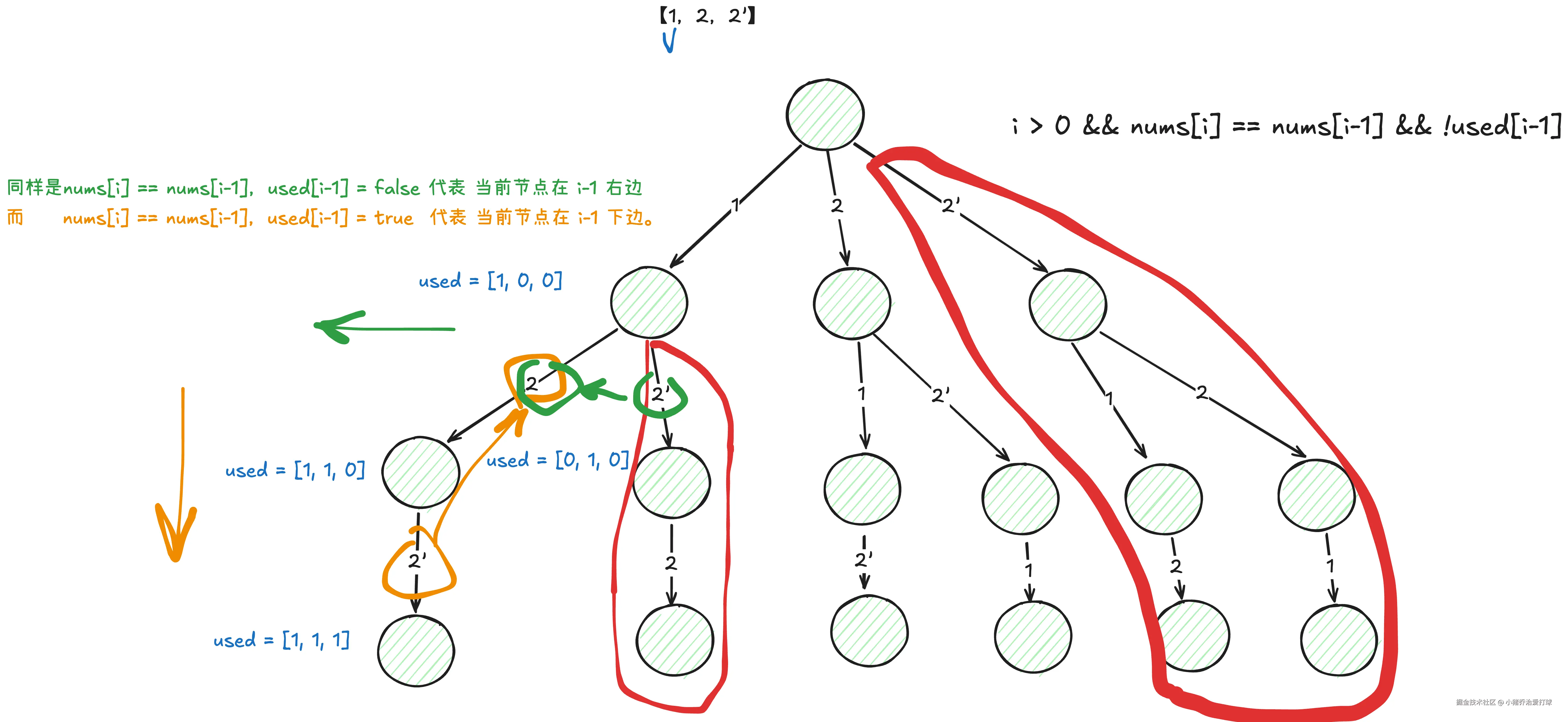

例题：LCR 084. 全排列 II

代码：

func permuteUnique(nums []int) (res [][]int) {
    sort.Ints(nums)
    path := []int{}
    used := make([]bool, len(nums))
    var dfs func(nums []int, used []bool)
    dfs = func(nums []int, used []bool) {
        if len(path) == len(nums) {
            res = append(res, append([]int(nil), path...))
            return
        }
        for i := range nums {
            if i > 0 && nums[i] == nums[i-1] && !used[i-1] {
                continue
            }
            if used[i] {
                continue
            }
            path = append(path, nums[i])
            used[i] = true
            dfs(nums, used)
            used[i] = false
            path = path[:len(path)-1]
        }
    }
    dfs(nums, used)
    return
}

3.2 组合/子集

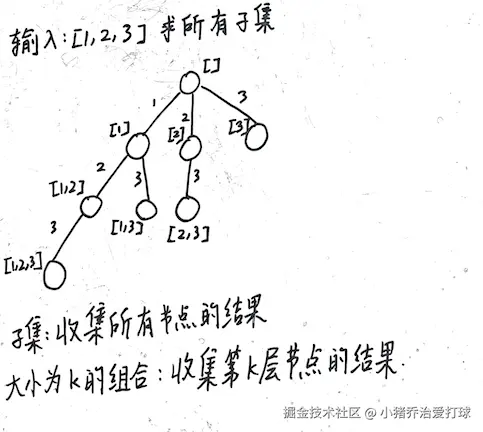
3.2.1 什么是组合？

输入: n = 4, k = 2 （n代表可以选择的元素是1，2 ... n, k代表从中选出2个元素）
输出:
[
  [2,4],
  [3,4],
  [2,3],
  [1,2],
  [1,3],
  [1,4],
]

3.2.2 什么是子集？

输入： nums = [1,2,3]
输出： [[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

3.2.3 如何思考：子集/组合树

组合/子集树：

3.3 condition-1: 元素无重，不可复选

3.3.1 组合

例题：LCR 080. 组合

代码：

func combine(n int, k int) (res [][]int) {
    var dfs func(n, start int, path []int)
    dfs = func(n, start int, path []int) {
        if len(path) == k {
            tmp := make([]int, k)
            copy(tmp, path)
            res = append(res, tmp)
            return
        }
        for i := start; i <= n; i++ {
            path = append(path, i)
            dfs(n, i + 1, path)
            path = path[:len(path)-1]
        }
    }
    path := []int{}
    dfs(n, 1, path)
    return
}

3.3.2 子集

例题：LCR 079. 子集

代码：

func subsets(nums []int) (res [][]int) {
    var dfs func(nums []int, path []int, start int)
    dfs = func(nums, path []int, start int) {
        tmp := make([]int, len(path))
        copy(tmp, path)
        res = append(res, tmp)
        for i := start; i < len(nums); i++ {
            path = append(path, nums[i])
            dfs(nums, path, i+1)
            path = path[:len(path)-1]
        }
    }
    path := []int{}
    dfs(nums, path, 0)
    return
}