25_7_7
第二题:两个数组的交集_牛客题霸_牛客网
本题采用哈希,因为哈希查找速度极快
当数据个数上限不大时,可以不用定义真正的哈希表,自己用数组模拟一个哈希表,提高效率
自己做题时开辟了真正的哈希表,更优算法如下:
class Solution
{
public:
vector<int> intersection(vector<int>& nums1, vector<int>& nums2)
{
vector<int> ans;
vector<bool> hash(1000, false);
for(auto i : nums1)
{
hash[i] = true;
}
for(int i = 0; i < nums2.size(); i++)
{
if(hash[nums2[i]] == true)
{
ans.push_back(nums2[i]);
hash[nums2[i]] = false;
}
}
return ans;
}
};第三题:点击消除_牛客题霸_牛客网
利用栈的思想,类似于之前括号匹配那一题
我开始写的时候的思路:遍历字符串,和后面一样就string::erase删除迭代器区间,和前面一样也是;但是这样i可能在一次删除之后指向无效的位置
正确解法:
这里的ans最后的元素总是和str下一个元素相比较,所以要将进栈的操作放在比较的后面
#include <iostream>
#include<stack>
using namespace std;
int main()
{
string str, ans;
cin >> str;
for(auto ch : str)
{
if(str.size() && ans.back() == ch) ans.pop_back();
else ans.push_back(ch);
}
if(ans.size() == 0 ) cout<< "0";
else cout << ans;
return 0;
}25_7_8
第一题:牛牛的快递_牛客题霸_牛客网
我自己写的:利用sum反求整数部分
题解中有两种方法取得整数
1、ceil函数向上取整
2、num-(int)num,取得这个数的小数部分
#include <iostream>
using namespace std;
int main()
{
float a = 0.0;
char b;
cin >> a >> b;
int sum = 0;
if(a <= 1.0) sum += 20;
else
{
sum += 20 + (a - 1) / 1;
float c = a - 1 - (sum - 20) / 1;
if(c) sum += 1;
}
if(b == 'y') sum += 5;
cout << sum;
return 0;
}
//1、ceil(a)
//2、c - (int)c第二题:最小花费爬楼梯_牛客题霸_牛客网
使用动态规划
每一次处于一个台阶时,是从前面一个或者两个位置的台阶跳上来的;那么dp数组为跳到这个台阶之前总的花费,cost数组为跳离当前台阶的花费;那么:
dp[i] = min(dp[i-1] + cost[i-1] , dp[i-2] + cost[i-2])(状态转移方程)
由左向右填写方程,初始时,dp[0] = 0,dp[1] = 0,最后要算到dp[n]
cpp
#include <iostream>
#include<vector>
using namespace std;
int main()
{
int n = 0;
cin >> n;
vector<int> cost(n);
for(int i = 0; i < n; i++)
cin >> cost[i];
vector<int> dp(n+1);
dp[0]=0; dp[1]=0;//初始状态
for(int i = 2; i <= n; i++)
{
dp[i] = min(dp[i-1] + cost[i-1] ,dp[i-2] + cost[i-2]);
}
if(n == 1)
cout << cost[0];
else
cout << dp[n];
return 0;
}第三题:数组中两个字符串的最小距离
我的思路:
cpp
int main() {
int n = 0;
string str1;
string str2;
cin >> n;
cin >> str1 >> str2;
vector<string> strs(n);
for (int i = 0; i < n; i++)
cin >> strs[i];
int gap = INT_MAX, p1 = -1, p2 = -1;
//p1指向str1的位置,p2指向str2的位置
//先从头开始找,找到p1或者p2作为基点之后再往后找p1或者p2
//若是基点为p1,而后面先找到的是str1,那么更新p1;若是先找到的是str2,计算gap
//之后在前面的作为基点重复操作,因为p1和p2之间不可能存在str1或者str2了
for (int i = 0; i < n; i++) {
if (strcmp(str1.c_str(), strs[i].c_str()) == 0) p1 = i;
else if (strcmp(str2.c_str(), strs[i].c_str()) == 0) p2 = i;
if (p1 != -1 && p2 != -1)
gap = abs(p1 - p2) < gap ? abs(p1 - p2) : gap;
}
cout << (gap == INT_MAX ? -1 : gap);
return 0;
}题解思路:
贪心算法:每次找到一个匹配字符串之后往前找另一个字符串即可,这样不会漏掉,因为后面的当指针遍历到它时,又会向前找
具体地定义两个指针p1,p2分别指向str1,str2;然后找字符串,每次p1或者p2向前找p2或者p1,计算gap,小就更新
cpp
int main()
{
int n = 0;
string str1, str2;
cin >> n;
cin >> str1 >> str2;
vector<string> strs(n);
for (int i = 0; i < n; i++)
cin >> strs[i];
int p1 = -1, p2 = -1, gap = INT_MAX;
for (int i = 0; i < n; i++)
{
if (strs[i] == str1)
{
if (p2 != -1)
{
gap = min(i - p2, gap);
}
p1 = i;
}
else if (strs[i] == str2)
{
if (p1 != -1)
{
gap = min(i - p1, gap);
}
p2 = i;
}
}
if (gap == INT_MAX) cout << -1;
else cout << gap;
return 0;
}25_7_9
第一题:简写单词_牛客题霸_牛客网
我的代码:读取整个字符串,找到空格之后找下一个字母,并且转为大写
string中find接口:
| string (1) |
size_t find (const string& str, size_t pos = 0) const;|
| c-string (2) |size_t find (const char* s, size_t pos = 0) const;|
| buffer (3) |size_t find (const char* s, size_t pos, size_t n) const;(n表示匹配查找的个数) |
character (4) size_t find (char c, size_t pos = 0) const;
getline接口:(无视空格读取一行字符串)
istream& getline (istream& is, string& str);使用:string str;getline(cin , str);
cpp
int main()
{
string str;
getline(cin, str);
string ans;
ans += str[0];
size_t pos = str.find(' ');
while(pos != string::npos)
{
ans += str[pos + 1];
pos = str.find(' ', pos + 1);
}
for (auto& ch : ans)
{
if (ch >= 97 && ch <= 122)
ch -= 32;
}
cout << ans;
}题解思路:
就是用cin读取每次读取空格分开的一个单词,之后取得每个单词开头第一个字符,直到读取完毕
cpp
// int main()
// {
// string str;
// while(cin >> str)//跳过空格
// {
// if(str[0] >= 97 && str[0] <= 122) cout << (char)(str[0] - 32);
// else cout << str[0];
// }
// return 0;
// }第二题:dd爱框框
我的思路:滑动窗口
cpp
//滑动窗口
//首先要找最小区间,用两个指针,一个指针p1固定,另一个p2遍历
//遍历过程中一旦两个指针内的数加起来>=20那么此时的区间就是固定p1处得出最小的
//因为p2向后走区间内加起来肯定>=20但是区间一直变大
//当有>=20的时候就移动固定的p1,找更小的区间
//当>=20且新区间小于旧区间长度时就记录l和r,
int main()
{
int n = 0, x = 0;
cin >> n >> x;
vector<int> a(n);
for (int i = 0; i < n; i++)
cin >> a[i];
int p1 = 0, p2 = 0;
int size = n, sum = 0;
int l = 0, r = 0;
while (p2 <= n)
{
if (sum < x)
sum += a[p2++];
else
{
if (p2 - p1 < size)
{
l = p1;
r = p2 - 1;
size = p2 - p1;
}
sum -= a[p1++];
}
}
cout << l + 1 << ' ' << r + 1;
return 0;
}第三题:除2!
反思:做这题时这题思路是对的,代码有一个问题,没有考虑数据范围,要使用long long;之后都用long long吧
cpp
#include <functional>
#include <iostream>
#include<queue>
#include<vector>
using namespace std;
typedef long long LL;
//每次取最大的偶数进行/2操作
//利用优先级队列,结束看priority_queue参数怎么传
struct Less
{
bool operator()(const LL& x, const LL& y)
{
return x < y;
}
};
int main()
{
//准备部分
LL n = 0, k = 0;
cin >> n >> k;
vector<LL> a(n, 0);
priority_queue<LL, vector<LL>, Less> pq;
LL sum = 0, sum1 = 0, sum2 = 0;//总和、奇数和、偶数和
for (int i = 0; i < n; i++)
{
cin >> a[i];
if (a[i] % 2 == 0) pq.push(a[i]);
else sum1 += a[i];
}
//处理k次
for (int i = 0; i < k; i++)
{
if (pq.empty()) break;
//除2之后可能不是偶数,是偶数入队列,不是加到sum1即可
LL tmp = pq.top() / 2;
pq.pop();
if (tmp % 2 == 0) pq.push(tmp);
else sum1 += tmp;
}
//统计sum2偶数部分的和
while (!pq.empty())
{
sum2 += pq.top();
pq.pop();
}
sum = sum1 + sum2;
cout << sum;
return 0;
}25_7_10
第一题:Fibonacci数列
利用滚动的三个数模拟斐波那契数列,当n<c的时候计算出n距离b和c的距离,输出较小值即可
#include <iostream>
using namespace std;
int main()
{
int n = 0;
cin >> n;
int a = 0, b = 1, c = 1;
while(n > c)
{
a = b;
b = c;
c = a + b;
}
cout << min(n - b, c - n);
return 0;
}
// 64 位输出请用 printf("%lld")第二题:单词搜索
class Solution
{
int m, n;
bool vis[101][101] = { 0 };
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
public:
bool exist(vector<string>& board, string word) {
m = board.size(), n = board[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (board[i][j] == word[0]) {
if (dfs(board, i, j, word, 0)) return true;
}
}
}
return false;
}
bool dfs(vector<string>& board, int i, int j, string& word, int pos) {
if (pos == word.size() - 1) {
return true;
}
vis[i][j] = true;
for (int k = 0; k < 4; k++) {
int a = i + dx[k], b = j + dy[k];
if (a >= 0 && a < m && b >= 0 && b < n && !vis[a][b] && board[a][b] == word[pos + 1]) {
if (dfs(board, a, b, word, pos + 1)) return true;
}
}
vis[i][j] = false;
return false;
}
};25_7_11
第二题: 腐烂的苹果_牛客题霸_牛客网
多源BFS+最短优先路径
cpp
class Solution {
int m, n;
int dx[4] = {0, 0, 1, -1};
int dy[4] = {1, -1, 0, 0};
bool vis[1010][1010] = { 0 };
public:
int rotApple(vector<vector<int> >& grid) {
m = grid.size(), n = grid[0].size();
queue<pair<int, int>> q;
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (grid[i][j] == 2)
q.push({i, j});
int ret = 0;
while (q.size()) {
int sz = q.size();
ret++;
while (sz--) {
auto [a, b] = q.front();
q.pop();
for (int i = 0; i < 4; i++) {
int x = a + dx[i], y = b + dy[i];
if (x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1
&& !vis[x][y]) {
vis[x][y] = true;
q.push({x, y});
}
}
}
}
for (int i = 0; i < m; i++)
for (int j = 0; j < n; j++)
if (grid[i][j] == 1 && !vis[i][j])
return -1;
return ret - 1;
}
};第三题:孩子们的游戏(圆圈中最后剩下的数)_牛客题霸_牛客网
约瑟夫环:
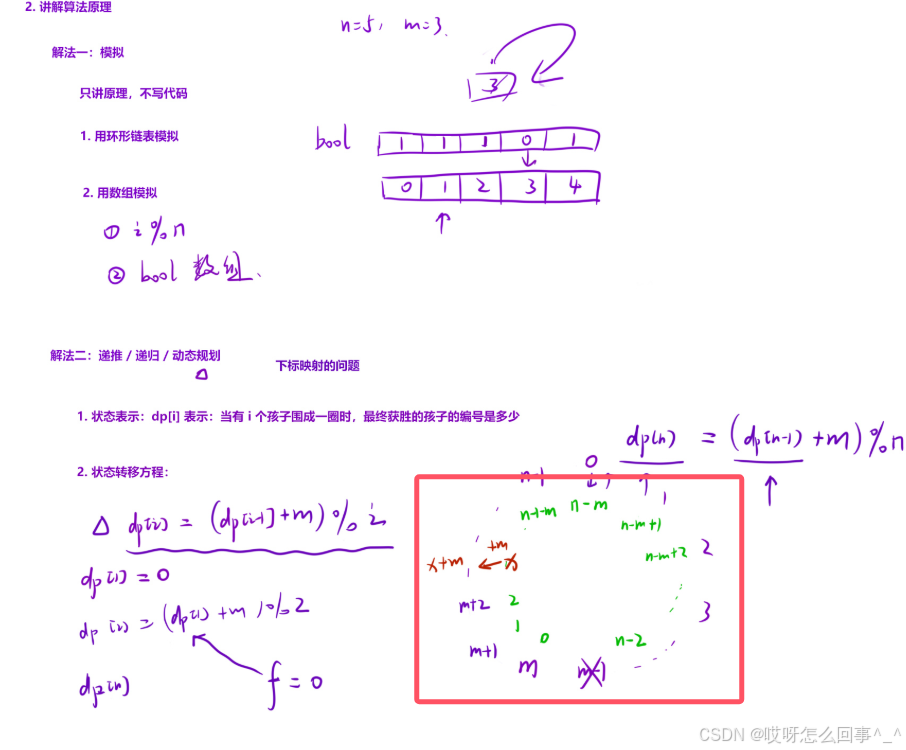
使用动态规划的方法可解:
dp[i]表示i个孩子时最后剩下的孩子编号(即下标)
假设现有n个孩子,最后剩下的就是dp[n],那么删除m-1下标的孩子之后还剩下n-1个孩子;将这n-1个孩子围成一个新的圈,最后剩下的就是dp[n-1],这个新圈开始编号时和旧圈的编号的关系是:新圈编号加上m等于旧圈编号;那么就有dp[n] = (dp[n-1] + m) % n(为了防止m过大),这两个圈实际上是一个圈,新圈的下标是删除了一个之后重新开始数到m-1的编号,从新圈中数出来m-1位置之后要还原成旧圈即本来的下标,就要+m
class Solution {
public:
int LastRemaining_Solution(int n, int m) {
// vector<int> dp(n + 1, 0);
// for(int i = 2; i <= n; i++)//i为围成圈的孩子的数量
// {
// dp[i] = (dp[i - 1] + m) % i;
// }
// return dp[n];
//空间优化的写法:
int f = 0;//一个孩子的时候
for(int i = 2; i <= n; i++)//i表示有几个孩子
{
f = (f + m) % i;
}
return f;
}
};25_7_12
第三题:大数乘法_牛客题霸_牛客网
计算这种大数相乘、大数相加的问题不能够直接用数字因为数据太大会溢出,要模拟每一位相乘的过程
先用数组记录两个数字位相乘的结果,并且放到下标为这两个数字在各自字符串下标相加的位置上,这样最后算进位时结果正确
class Solution {
public:
/**
* 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可
*
*
* @param s string字符串 第一个整数
* @param t string字符串 第二个整数
* @return string字符串
*/
string solve(string s, string t) {
// write code here
if(s == "0" || t == "0") return "0";
reverse(s.begin(), s.end());
reverse(t.begin(), t.end());
int n = s.size(), m = t.size();
vector<int> arr(n + m - 1, 0);
//无进位相乘相加
for(int i = 0; i < n; i++)
{
for(int j = 0; j < m; j++)
{
arr[i + j] += (s[i] - '0') * (t[j] - '0');
}
}
//最后统一进行进位处理
string ans;
int tmp = 0;//进位
for(int i = 0; i < arr.size(); i++)
{
arr[i] += tmp;
tmp = arr[i] / 10;//进位
arr[i] %= 10;//本位
ans += arr[i] + '0';
}
if(tmp) ans += tmp + '0';
reverse(ans.begin(), ans.end());
return ans;
}
};25_7_10的第二题和25_7_11的第二题学完对应算法课之后在学习