从0开始学习R语言--Day52--weibull

在分析带有状态变化特征的数据时（如医疗数据的结局特征，手机电池的寿命等等），我们需要分析得不只是什么时候什么时候出发结局，还要分析特征的稳定性，比如电池的续航在初期不稳定，预测里可能两个月就会坏，但用了一个月后手机稳定下来，预测可能就变成用一年都不会坏。weibull分布能帮我们捕捉这种特征，从而能够做后续的处理（比如维修计划，对病人的结局分析作进一步拆解）。

以下是一个例子：

R 复制代码

# 加载必要的包
library(ggplot2)
library(MASS)
library(fitdistrplus)  # 提供更稳健的拟合方法

# 1. 生成更理想的Weibull分布数据集
set.seed(123)
n <- 1000
shape <- 1.5
scale <- 2.0

# 生成数据并添加保护措施
weibull_data <- rweibull(n, shape = shape, scale = scale)
weibull_data <- pmax(weibull_data, .Machine$double.eps)  # 确保严格大于0

# 2. 方法一：使用fitdistrplus包（更稳健）
fit_fitdistrplus <- fitdist(weibull_data, "weibull", 
                            method = "mle",  # 最大似然估计
                            control = list(trace = 0),  # 关闭冗长输出
                            lower = c(shape = 0.1, scale = 0.1))  # 参数下限

# 显示拟合结果
summary(fit_fitdistrplus)

# 3. 方法二：手动优化（完全控制过程）
# 定义负对数似然函数
weibull_nll <- function(params, data) {
  shape <- params[1]
  scale <- params[2]
  if(shape <= 0 || scale <= 0) return(Inf)  # 参数必须为正
  -sum(dweibull(data, shape = shape, scale = scale, log = TRUE))
}

# 使用optim进行优化
initial_params <- c(shape = 1, scale = 1)  # 初始值
optim_result <- optim(initial_params, 
                      weibull_nll, 
                      data = weibull_data,
                      method = "L-BFGS-B",
                      lower = c(0.1, 0.1),
                      upper = c(10, 10))

if(optim_result$convergence == 0) {
  cat("\n手动优化结果:\n")
  cat("估计形状参数:", round(optim_result$par["shape"], 4), "\n")
  cat("估计尺度参数:", round(optim_result$par["scale"], 4), "\n")
} else {
  cat("优化未收敛\n")
}

# 4. 可视化比较
par(mfrow = c(1, 2))
# 直方图与拟合密度
hist(weibull_data, prob = TRUE, breaks = 30, col = "lightblue",
     main = "Weibull分布拟合")
curve(dweibull(x, shape = shape, scale = scale), 
      col = "red", lwd = 2, add = TRUE)  # 真实分布
curve(dweibull(x, shape = fit_fitdistrplus$estimate["shape"],
               scale = fit_fitdistrplus$estimate["scale"]),
      col = "blue", lwd = 2, lty = 2, add = TRUE)  # 拟合分布
legend("topright", legend = c("真实", "拟合"), 
       col = c("red", "blue"), lty = 1:2, lwd = 2)

# QQ图
qqplot(qweibull(ppoints(weibull_data), 
                shape = fit_fitdistrplus$estimate["shape"],
                scale = fit_fitdistrplus$estimate["scale"]),
       weibull_data,
       main = "Weibull QQ图",
       xlab = "理论分位数", ylab = "样本分位数")
abline(0, 1, col = "red")

输出：

R 复制代码

Fitting of the distribution ' weibull ' by maximum likelihood 
Parameters : 
      estimate Std. Error
shape 1.511529  0.0356495
scale 2.012800  0.0488228
Loglikelihood:  -1480.976   AIC:  2965.953   BIC:  2975.768 
Correlation matrix:
          shape     scale
shape 1.0000000 0.2164548
scale 0.2164548 1.0000000

手动优化结果:
估计形状参数: 1.5116 
估计尺度参数: 2.0128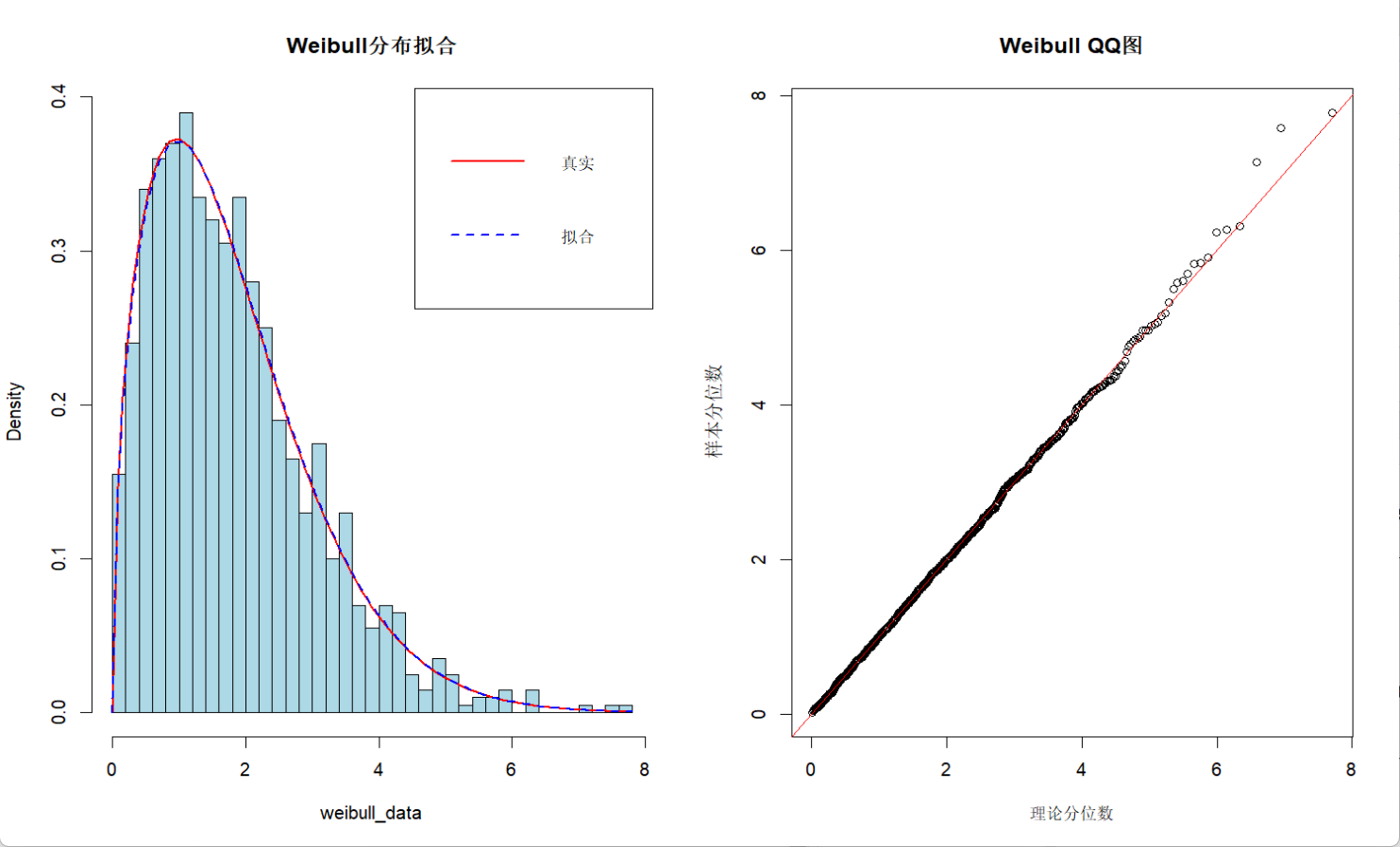

输出中的形状参数和尺度参数都和真实值非常接近，说明模型的结果很精确；直方图和红色曲线图基本重合，说明数据非常符合分布，而QQ图中大部分数据点也都落在了对角线上，进一步说明了结果的可靠性。