图论——Djikstra最短路

原理解释

首先解释一下它大概的应用场景以及原理：现在有这么一张图，图上各点之间都有一定的边权或者说是距离。给定你一个起点（例如点1），让你求这个点到图上所有点的最短距离是多少？

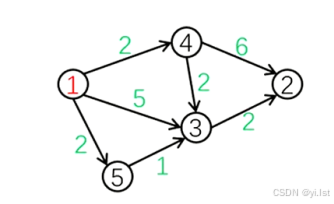
这个问题比较平常，但是突然这么一问如果之前没有学过此算法肯定一脸懵。接下来简单解释一下算法的实现思路。

实现思路

• 定义一个距离数组d\[\]表示起点到此点的最短距离，除了此时的点全部赋为inf

• 定义一个标记数组v\[\]用来判断此点是否访问过，避免重复访问

• 对于这个点，每次对它的出点进行遍历，找到距离最小的点处理

• 如果说此时这条路径到达一个点比之前的路径到达它的距离短，就进行更新

  • 例如点1到点3：
  • 原本是1->3，距离为5
  • 后来路径为1->4->3，距离为4
  • 此时就可以对d3进行更新

• 最后输出d数组就是起点到所有点的距离了

实现过程演示

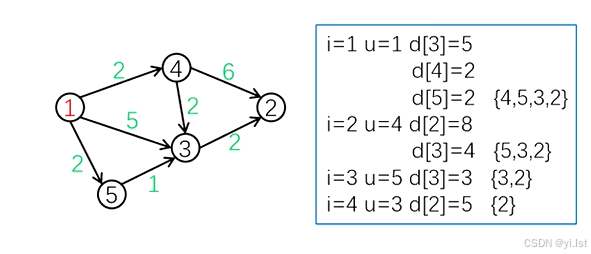
代码

vector<pii> e[N];
int d[N],vis[N];
void dji(int s)
{
	for(int i=0; i<=n; i++) d[i]=INF;
	d[s]=0;
	for(int i=1; i<n; i++)//遍历枚举所有点
	{
		int u=0;
		for(int j=1; j<=n;j++)//每次找到此点出点的距离最近点
			if(!vis[j]&&d[j]<d[u]) u=j;
		vis[u]=1;//此点已经当过入点
		for(auto ed:e[u])//对它所有出点进行贪心处理
		{
			int v=ed.v,w=ed.w;
			if(d[v]>d[u]+w)
				d[v]=d[u]+w;
		}
	}
}
void solve()
{
	cin >> n >> m >> s;//点数、边数、起点
	for(int i=0; i<m; i++)
	{
		cin >> a >> b >> c;
		e[a].push_back({b,c});
	}
	dgi(s);
	for(int i=1; i<=n; i++) cout << d[i] << ' ';
}

---

优化处理

不难看出，这版代码一共用了三个for循环，最多嵌套了两层。时间复杂度极其高，达到了 O ( n 2 + m ) O(n^{2}+m) O(n2+m)，所以我们可以对它进行优化处理。

直接跳到时间复杂度最高的地方：找离入点距离最近的出点。如果说此时我们用优先队列的最小堆来维护距离的话，堆顶的元素就一直是离入点最小的了，这样我们就省去了去枚举再遍历着找的步骤。

实现过程演示

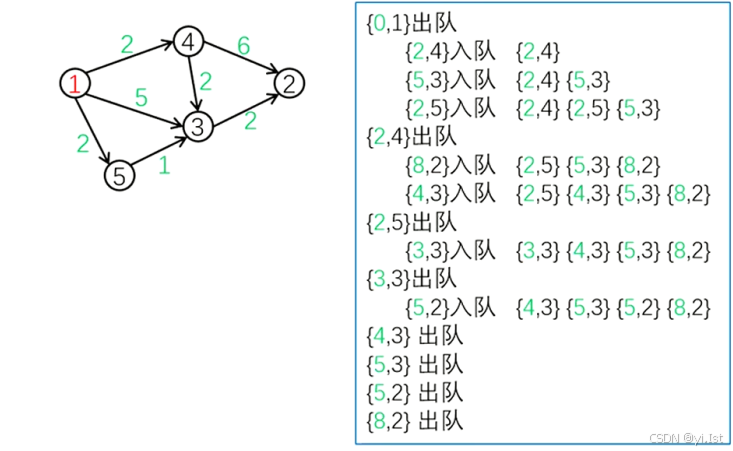
代码

priority_queue<pii,vector<pii>,greater<pii>> q;
void dji(int s)//当前点
{
	for(int i=0; i<=n; i++) d[i]=INT_MAX;
	d[s]=0;q.push({0,s});
	while(!q.empty())
	{
		auto t=q.top(); q.pop();
		int u=t.se;
		if(vi[u]) continue;
		vi[u]=1;
		for(auto ed:a[u])
		{
			int v=ed.fi,w=ed.se;
			if(d[u]+w<d[v])//当前路到此点距离比之前更优
			{
				d[v]=d[u]+w;
				q.push({d[v],v});
			}
		}
	}
}
void solve()
{
	cin >> n >> m >> s;//总点数、边的数量、出发点编号
	for(int i=0; i<m; i++)
	{
		int u,v,w;
		cin >> u >> v >> w;
		a[u].push_back({v,w});
	}
	dji(s);
	for(int i=1; i<=n; i++) cout << d[i] << ' ';
}

---

例题演示

下面看一道类似的例题：B-代价转移

思路

虽然此题看着并没有图，但是Djikstra算法该有的东西此题都能对应上

• 代价C1,C2,C3看作操作的距离
• 目前的点就是入点，三种操作之后的数分别代表三个出点
• 如果a更大的话直接相减就行

代码

void dji()
{
	fill(v,v+N,0);//多实例重置数组
    fill(k,k+N,INF);//赋值
	priority_queue<pii,vector<pii>,greater<pii>> q;
	k[a]=0;//由于要从此点开始，所以设为0
	q.push({0,a});//将起点入队
	maxx=b*2;//所有数中最大可能值,用于边界判断
	while(!q.empty())
	{
		auto [val,num]=q.top();//将当前点之前的值取出来（之前是出点）
		q.pop();
		if(v[num]) continue;//此值当过入点，跳过
		v[num]=1;//此时它是入点，标记
		pii cu[]={{num+1,c1},{num-1,c2},{num*2,c3}};//当前可以到的点
		for(auto [x,y]:cu)
		{
			if(x<1||x>maxx) continue;//边界处理
			if(k[num]+y<k[x])//如果此时的选择比它之前的更优
			{
				k[x]=k[num]+y;//赋值、入队
				q.push({k[x],x});
			}
		}
	}
	cout << k[b] << endl;
}
void solve()
{
	cin >> a >> b >> c1 >> c2 >> c3;
	if(a>=b)//b小的话就只能减了
	{
		cout << (a-b)*c2 << endl;
		return ;
	}
	dji();
}

---

之前没学的时候总觉得这算法光听名字就很高级，应该还很难。其实它就是一套比较成体系的贪心思想，将图画出来进行演示的话还是比较好理解的。