一种可扩展且可用于生产环境的天空与大气渲染技术

图 1：使用本文提出的方法渲染的不同大气条件和视角的图像。从左到右：类地球白天的地面视图、类火星蓝色日落的地面视图、类地球行星的太空视图以及艺术化构想的小行星视图。

摘要

我们提出了一种基于物理的方法，用于渲染从地面到太空视角的行星大气。我们的方法计算成本低，与以往成功的方法相比，不需要任何高维查找表（LUTs），因此不会出现与高维查找表相关的视觉伪影。我们还提出了一种新的近似方法，用于实时评估大气中的光多次散射。我们重新审视了渲染自然大气效果的意义，并提出了一组简单的查找表和参数化方法来渲染天空及其空气透视效果。大气成分可以动态变化，以匹配艺术构想和天气变化，而无需进行大量的查找表更新。这种完整技术可用于实时应用，如游戏、模拟器或建筑预可视化。该技术的适用范围从能效高的移动平台到配备高端 GPU 的个人电脑，还可用于加速路径追踪。

CCS 概念

・计算方法学￫光栅化；光线追踪；

1. 引言

渲染自然现象对于可信世界的视觉模拟至关重要。大气模拟和渲染对于需要具有动态时间变化的大型开放世界，或从太空观测行星的应用来说非常重要。这类应用包括游戏、建筑可视化以及飞行或太空模拟器。然而，当前的方法存在局限性：它们要么仅限于地面视角，只能表示单一类型的大气，在大气属性变化时需要计算昂贵的查找表（LUTs）更新，甚至可能出现视觉伪影。

我们提出了一种基于大气参与介质物理表示的方法，用于实时渲染行星的天空和空气透视效果。本文的贡献如下：

我们提出了一种天空和空气透视渲染技术，该技术依靠查找表以较低分辨率评估光照积分中计算昂贵的部分，同时保留重要的视觉特征。

我们提出了一种新的方法来评估大气中光多次散射的贡献。它可以近似无限多次的散射阶数，还可用于加速路径追踪。

该技术支持动态时间变化以及大气属性的动态更新，同时能在从低端苹果 iPhone 6s 到游戏主机和高端游戏电脑的各种设备上高效渲染。

这种方法已应用于 Epic Games 的虚幻引擎†。在本文中，我们将使用光度单位（亮度 / 照度）而非辐射单位（辐射亮度 / 辐射照度）。这是因为这些术语在现代游戏引擎中更为常用 [LdR14]。

在第 2 节回顾相关工作后，我们在第 3 节简要描述参与介质渲染（重点关注大气情况）。第 4 节介绍本文使用的大气材料模型，第 5 节详细阐述我们的大气渲染技术。第 6 节讨论结果，并与路径追踪的基准真值以及先前模型进行比较。最后，我们在第 7 节报告性能情况并得出结论。

1. 相关工作

第一波天空渲染技术的重点是从视点对大气进行光线步进。这是西田等人 [NSTN93] 首次提出的从地面和太空视角渲染大气的方法。奥尼尔 [ONe07] 为了提高性能，提出按顶点积分散射亮度，并在每个像素应用相位函数来渲染最终的天空颜色。温策尔 [Wen07] 提出了相同的想法，但将散射亮度存储在纹理中，通过多帧更新来分摊成本。这些模型的主要缺点是忽略了光的多次散射对天空外观的影响。

为了降低光线步进的成本并包含多次散射，已提出了基于实际测量 [PSS99] 或使用带有光谱信息的路径追踪生成的参考数据 [HW12] 拟合的解析模型。这些模型评估速度非常快，并且具有简单的参数化：例如，使用单一的混浊度值来表示空气中的气溶胶数量，从而使大气看起来更浓密。然而，它们仅限于地面视角，并且只能表示参数所拟合的单一大气类型。例如，当模型拟合地球天空时，无法渲染火星天空。

已提出更先进的模型用于渲染具有多次散射的大气效果，视角范围从地面到太空。西田 [NDN96] 提出将参与介质细分为体素，并模拟体素之间的能量交换。已提出的更经济的模型去除了体素表示：它们将计算昂贵的积分结果存储到查找表中，以便在运行时在 GPU 上轻松查询。这些查找表可以在运行时按像素采样（根据视图、太阳和世界信息）来计算透射率和散射亮度。Bruneton 和 Neyret [BN08] 提出了 4D 查找表，而 Elek [Ele09] 舍弃了一个维度，实际上忽略了太阳刚落到地平线以下时可见的行星对大气的遮挡。因为在这些模型中，从视点到网格表面的散射是通过从查找表中采样两个值并相减来评估的，所以由于分辨率和参数化精度问题，在地平线处可能会出现视觉伪影。Yusov [Yus13] 通过更好的参数化改进了这种情况，这对于类地球大气非常有效。然而，在大气更浓密的情况下，伪影仍然可能可见。对于这些基于查找表的模型中的每一个，多次散射都是通过迭代评估散射查找表来实现的：从先前散射阶数的查找表中采样散射亮度，以评估新的查找表。当将所有这些加在一起时，就形成了具有高达迭代次数的多次散射阶数的最终散射查找表。然而，当游戏需要更新大气属性时（例如，由于天气条件变化或为了匹配艺术指导），这些查找表的更新很麻烦。可以分时更新，但这会导致太阳移动和天空颜色之间出现视觉延迟 [Hil16]。基于查找表的模型的源代码可在网上获取 [Bru17b; Yus13]，并已在多个游戏中成功使用 [Hil16; dCK17; Bau19]。此外，Bruneton [Bru17a] 广泛讨论了所有这些模型，并比较了它们的优缺点。

渲染大气时的挑战之一是表示山丘和山脉造成的体积阴影。可以依靠对极线 [Yus13]、阴影体 [Bru17b] 或从阴影图中拉伸网格的阴影体变体 [Hoo16]。这些技术速度快，但只能表示不透明网格的清晰阴影。它们无法渲染由云参与介质或太阳圆盘面光源阴影半影产生的软阴影。在捕捉这种柔和细节方面，光线步进仍然具有明显优势。

1. 参与介质渲染

可以使用光线步进或路径追踪来渲染参与介质。在这两种情况下，都需要使用材料参数化来表示参与介质，如辐射传输方程所描述的 [FWKH17]。在这个框架中，对于给定位置和考虑沿某一方向传播的光束，每个波长的吸收系数 σₐ和散射系数 σₛ（单位：m⁻¹）分别表示沿该方向被吸收或散射的辐射亮度比例。消光系数 σₜ=σₐ+σₛ表示由于吸收和外散射造成的总能量损失。此外，当发生散射事件时，需要根据相位函数 P（单位：sr⁻¹）表示的分布来确定散射方向。

在严格的实时约束下，我们的方法依靠光线步进首先评估单次散射，如图 2 所示。

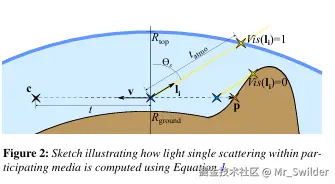
它假设有一组定向光源，例如太阳和月亮。它还考虑了一个虚拟行星，其地面根据反照率 ρ 具有纯漫反射响应。它涉及对朝向观察者的散射亮度 L 进行积分，该积分是介质透射率、阴影因子（包括来自行星的阴影和来自大气的阴影）以及沿路径段的散射的函数，使用以下公式：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L ( c , v ) = T ( c , p ) L o ( p , v ) + ∫ t = 0 ∥ p − c ∥ L s c a t ( c , c − t v , v ) d t , ( 1 ) L(c, v)=T(c, p) L_{o}(p, v)+\int_{t=0}^{\| p-c\| } L_{scat }(c, c-t v, v) d t, \quad(1) </math>L(c,v)=T(c,p)Lo(p,v)+∫t=0∥p−c∥Lscat(c,c−tv,v)dt,(1)

<math xmlns="http://www.w3.org/1998/Math/MathML"> T ( x a , x b ) = e − ∫ x = x a x b σ t ( x ) ∥ d x ∥ , T\left(x_{a}, x_{b}\right)=e^{-\int_{x=x_{a}}^{x_{b}} \sigma_{t}(x)\| d x\| }, </math>T(xa,xb)=e−∫x=xaxbσt(x)∥dx∥,

<math xmlns="http://www.w3.org/1998/Math/MathML"> L s c a t ( c , x , v ) = σ s ( x ) ∑ i = 1 N l i g h t T ( c , x ) S ( x , l i ) p ( v , l i ) E i , L_{scat }(c, x, v)=\sigma_{s}(x) \sum_{i=1}^{N_{light }} T(c, x) S\left(x, l_{i}\right) p\left(v, l_{i}\right) E_{i}, </math>Lscat(c,x,v)=σs(x)∑i=1NlightT(c,x)S(x,li)p(v,li)Ei,

<math xmlns="http://www.w3.org/1998/Math/MathML"> S ( x , l i ) = V i s ( l i ) T ( x , x + t a t m o l l i ) , S\left(x, l_{i}\right)=V i s\left(l_{i}\right) T\left(x, x+t_{atmol} l_{i}\right), </math>S(x,li)=Vis(li)T(x,x+tatmolli),

其中，c 是视图相机位置，v 是当前位置朝向视图的方向，p 是表面交点，tₐₜₘₒₗ是与大气顶部边界的光线相交距离，Lₒ是 p 处的亮度（例如，虚拟行星地面上的光照）。lᵢ和 Eᵢ是第 i 个光源的方向和照度（考虑定向光源）。

在本文中，我们将我们的新光线步进方法与路径追踪器的结果进行比较。我们的路径追踪器在 GPU 上实现，能够实时以交互帧率可视化正在细化的结果。它使用蒙特卡洛积分，在参与介质中采用 delta 跟踪和重要性采样 [FWKH17]。它还利用比率跟踪 [NSJ] 来更快地收敛以估计透射率。这被视为我们的基准真值。

4. 大气模型

我们使用的大气材料模型在先前的论文中已有描述 [BN08; Bru17a]。我们专注于类地行星的模拟，即由岩石或金属构成的固体部分（我们称之为地面）。行星的地面和大气顶部边界用具有恒定半径的球体表示。变量 h 表示地面以上的高度。对于地球，地面半径为 6371km，大气顶部半径可设置为 6471km，代表 100km 的参与介质层。我们认为地面是具有均匀反照率 ρ=0.3 的纯漫反射材料 [NAS]。在渲染大气参与介质时，我们不像 [Ele09] 那样考虑广泛的光谱表示。相反，我们专注于典型的基于 RGB 的渲染。

大气由多种成分组成，要实现地球和其他行星的外观，所有这些成分都很重要：

瑞利理论描述了光与空气分子相互作用时的行为。我们假设光从不被吸收，只能发生散射 [BN08]。描述散射事件后光方向分布的相位函数为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> p r ( θ ) = 3 ( 1 + c o s ( θ ) 2 ) 16 π p_{r}(\theta)=\frac{3(1+cos (\theta)^{2})}{16 \pi} </math>pr(θ)=16π3(1+cos(θ)2)

其中 θ 是入射和出射散射方向之间的角度。

米氏理论描述了光与气溶胶（如尘埃或污染物）相互作用时的行为。光可以被散射或吸收。相位函数使用 Cornette-Shanks 相位函数近似 [GK99]：

<math xmlns="http://www.w3.org/1998/Math/MathML"> p m ( θ , g ) = 3 8 π ( 1 − g 2 ) ( 1 + c o s ( θ ) 2 ) ( 2 + g 2 ) ( 1 + g 2 − 2 g c o s ( θ ) ) 3 / 2 p_{m}(\theta, g)=\frac{3}{8 \pi} \frac{(1-g^{2})(1+cos (\theta)^{2})}{(2+g^{2})(1+g^{2}-2 g cos (\theta))^{3 / 2}} </math>pm(θ,g)=8π3(2+g2)(1+g2−2gcos(θ))3/2(1−g2)(1+cos(θ)2)

其中 g 是不对称参数，范围在 [-1,1]，决定了前向和后向散射的相对强度。默认情况下，g=0.8。请注意，使用更简单的 Henyey-Greenstein 相位函数也是合适的。

为简洁起见，在本文其余公式中，我们省略了这些相位函数的参数。我们还将各向同性相位函数表示为 <math xmlns="http://www.w3.org/1998/Math/MathML"> p u = 1 4 π p_{u}=\frac{1}{4 \pi} </math>pu=4π1。

表 1 列出了每种成分的散射和吸收系数 [Bru17a]。遵循瑞利和米氏理论的参与介质具有高度密度分布，分别为 <math xmlns="http://www.w3.org/1998/Math/MathML"> d r ( h ) = e − h 8000 m d^{r}(h)=e^{\frac{-h}{8000 m}} </math>dr(h)=e8000m−h和 <math xmlns="http://www.w3.org/1998/Math/MathML"> d m ( h ) = e − h 1200 m d^{m}(h)=e^{\frac{-h}{1200 m}} </math>dm(h)=e1200m−h。臭氧是地球的一种特定成分，已被确定为表示地球大气的重要成分，因为它是在太阳位于地平线时实现天空蓝色的关键 [Kut13]。臭氧不参与散射，只吸收光。按照 Bruneton [Bru17a; Bru17b] 的方法，我们将其分布表示为以 25km 高度为中心、宽度为 30km 的帐篷函数：

<math xmlns="http://www.w3.org/1998/Math/MathML"> d o ( h ) = m a x ( 0 , 1 − ∣ h − 25 ∣ 15 ) d^{o}(h)=max (0,1-\frac{|h-25|}{15}) </math>do(h)=max(0,1−15∣h−25∣)

表 1：构成地球大气的不同参与介质成分的系数。

类型	散射系数（×10⁻⁶ m⁻¹）	吸收系数（×10⁻⁶ m⁻¹）
瑞利	σᵣₛ = 5.802, 13.558, 33.1	σᵣₐ = 0
米氏	σₘₛ = 3.996	σₘₐ = 4.40
臭氧	σₒₛ = 0	σₒₐ = 0.650, 1.881, 0.085

5. 我们的渲染方法

5.1. 讨论：观察天空

现在我们描述天空和空气透视的视觉成分。这有助于证明我们在构建查找表和使用光线步进时所做选择的合理性。观察图 3，类地球天空的视觉频率较低，尤其是在白天：

瑞利散射是平滑的。
由于米氏散射相位函数产生的太阳周围光晕，对于自然界中常见的实际相位值，也是相当平滑的。
多次散射是渲染逼真图像的关键成分。如图 3（底行）所示，它的视觉频率也较低。
更高的频率在靠近地平线处可见，因为那里的大气迅速变得更浓密，因此光的参与更多。我们必须考虑到这一点。

大气中高频的主要来源是行星阴影（日落时）和山脉遮挡方程 3 中的单次散射事件产生的阴影。我们提出的解决方案可以两种模式渲染大气：禁用体积阴影，即利用天空视图查找表实现更快渲染（见第 5.3 节）；或启用体积阴影，即实现更精确但计算成本更高的渲染（见第 7 节）。

5.2. 透射率查找表

当执行光线步进以积分 Lₛₙₐₜ时，必须评估阴影项 S------ 表示大气介质对自身的遮挡。然而，对于每个单次散射样本，向太阳方向执行第二次光线步进将非常昂贵。为了加速这一过程，函数 T（x，x + tₐₜₘₒₗlᵢ）被存储为查找表，使用 Bruneton 和 Neyret [BN08] 第 4 节中描述的相同表示。

5.3. 天空视图查找表

鉴于构成大气的参与介质的整体低频率特性（见第 5.1 节），使用较少的样本进行光线步进应该足够了。然而，在 4K 或 8K 等高分辨率下，为每个像素执行此操作可能会很昂贵。鉴于天空的整体低视觉频率，我们应该能够以较低分辨率渲染天空，然后将其上采样到更高分辨率。

对于给定的视点，我们建议将远处的天空渲染到一个经纬纹理中，该纹理相对于行星地面上相机的局部上向量定向，以便地平线在其中始终是水平线。

例如，见图 4，上半部分代表天空，下半部分代表虚拟行星地面，地平线在中间。在第 5.1 节中，我们提到在靠近地平线处可见更高频率的视觉特征。为了更好地表示这些特征，我们在计算纹理坐标 v∈[0,1] 时对纬度应用非线性变换，这将在靠近地平线处压缩更多的纹素。使用简单的二次曲线：

<math xmlns="http://www.w3.org/1998/Math/MathML"> v = 0.5 + 0.5 ∗ s i g n ( l ) ∗ ∣ l ∣ π / 2 v=0.5+0.5 * sign(l) * \sqrt{\frac{|l|}{\pi / 2}} </math>v=0.5+0.5∗sign(l)∗π/2∣l∣

其中 l∈[-π/2, π/2]

这有效地在靠近地平线处压缩了更多像素，并改善了那里的细节量。如图 5 所示，这还有助于掩盖大气以较低分辨率渲染的事实。太阳圆盘不作为该纹理的一部分渲染，因为低分辨率和非线性映射会影响其呈现。它在应用天空视图查找表后进行合成。

5.4. 空气透视查找表

在渲染场景时，必须为不透明结构（如地形、山脉和建筑物）和半透明元素（如玻璃、火焰或其他参与介质，如云）渲染空气透视效果以保持一致性。因此，与希莱尔 [Hil16] 类似，我们在适合视图相机视锥体的体纹理中评估向相机的散射和透射率（见图 6）。散射存储在 RGB 通道中，而透射率存储在 A 通道中，作为与波长相关的 RGB 透射率的平均值。

我们使用的默认分辨率是屏幕上 32×32，在 32 公里的深度范围内有 32 个深度切片，这对于大多数应用和游戏来说已经足够。Epic Games 的《堡垒之夜》‡就是这种情况，其世界地图大小为 3km²，采用类地球风格化的大气设置。如果行星大气在某个点之前非常浓密，导致远处物体不太可见，则可以将深度范围调近到视点，以提高短距离的精度。

空气透视体纹理在评估光照后作为后处理应用于不透明物体，同时将天空视图查找表应用于屏幕。对于前向渲染管线中的透明元素，我们在顶点级别应用空气透视。这是因为透明元素在屏幕空间中通常相对于大气视觉变化较小。

5.5. 多次散射查找表

如第 2 节所述，先前的大气渲染技术 [BN08; Ele09; Yus13] 依靠迭代方法更新 3D 或 4D 查找表，每个散射阶数一次迭代。当渲染类地球大气时，这是一种可接受的解决方案，其中只需要 5 次多次散射阶数即可获得逼真的天空视觉效果。然而，当渲染更浓密的大气时，这很快变得不切实际，即当更高的散射阶数对大气外观很重要时，因此需要对查找表进行多次迭代。实际上，这种复杂度为 O (n)（其中 n 是散射阶数）的操作计算量太大。尤其是当艺术家不断更新大气属性以匹配不同时间的艺术指导或天气变化时。可以分时计算 [Hil16]，但这会导致更新延迟，这可能会影响其他系统的反应性，如全局光照或实时捕获的反射立方体贴图。

我们的目标是提出一种更廉价且即时的 O (1) 方法，该方法与散射阶数无关，能够在每一帧评估光的多次散射贡献，没有任何延迟。对于各种大气设置，保持正确性和可信度也是一项要求，以及能够在各种设备（从移动设备到高端 PC）上渲染大气。最后但同样重要的是，我们希望我们的方法基于物理的参与介质参数化，并保持能量守恒。

5.5.1. 关于我们近似方法的直觉构建

鉴于大气中参与介质的整体大尺度、长平均自由程和平滑分布，可以认为到达空间中某点的照度 E 对于其周围大面积内的所有点都是相同的。因此，由样本点周围更高阶的光散射事件产生的亮度积分可以通过对周围球体上的散射光进行积分来近似，这些相邻点接收相同的照度 E，同时考虑这些点之间的透射率。这种使用全局散射照度 E 作为输入，利用局部材料数据评估多次散射的想法，受到近似头发中光多次散射的双散射方法的启发 [ZYWK08]。

当光在介质中散射时，散射方向的分布很快变得各向同性 [JMLH01; Yan97]。为了提高性能，我们希望我们的多次散射查找表具有低维度。为此，我们假设散射阶数大于或等于 2 的光散射将按照各向同性相位函数发生，即没有任何优先方向。因此，在多次散射近似中，我们将忽略米氏和瑞利相位函数设置。我们认为这是一个可接受的近似，因为瑞利相位函数本来就是平滑的。为了更好地理解米氏散射情况下的近似，我们建议读者参考 Bouthors 对散射阶数相关的 BSDF 形状的分析 [Bou08]。

此外，已经表明二阶散射亮度与更高阶散射之间存在相关性 [HG13]。因此，我们建议将大气中的多次散射贡献评估为到达每个样本点的二阶散射亮度的函数。

我们的方法基于这些先前的结果，并将在第 5.5.3 节中详细描述。以下是其摘要，以及评估多次散射时的近似：

散射阶数大于或等于 2 的散射事件使用各向同性相位函数 pᵤ执行。
我们当前着色的位置附近的所有点都接收相同量的二阶散射光。
我们计算二阶散射贡献 L₂ₙd ₒᵣdₑᵣ和传递函数 fₘₛ（考虑沿高度的透射率和介质变化），该函数来自当前着色位置周围的参与介质。

最后，我们根据这些因素计算多次散射贡献 Ψₘₛ，模拟二阶光贡献在传递函数下从相邻点到当前着色位置的各向同性无限散射。

评估多次散射时忽略可见性 Vis。这基于这样一个事实，即光无论如何都会围绕山脉散射，例如，对于具有大平均自由程的自然大气，可见性的影响很小。

5.5.2. 查找表参数化

对于空间中的任何点，我们希望能够从查找表中存储和查询各向同性多次散射对亮度的贡献。鉴于我们认为虚拟行星是一个完美的球体，多次散射贡献是各向同性的，并且大气中介质的分布仅随高度变化，我们将此查找表表示为一个小的 2D 纹理。[0,1]² 中的 u，v 参数化如下：

u=0.5+0.5cos (θₛ)，其中 θₛ是太阳天顶角，s 表示其方向。

v=max (0, min ((h-R₉ᵣₒᵤₙd)/(Rₜₒₚ-R₉ᵣₒᵤₙd), 1))，其中样本位置 xₛ位于高度 h 处。

这种查找表及其参数化的示例可以在图 7 中看到。

5.5.3. 高散射阶数查找表评估

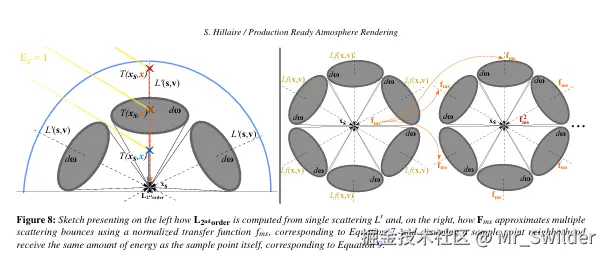
考虑位置 xₛ和高度 h 处的样本点，我们使用以下公式积分到达点 xₛ的二阶散射亮度 L₂ₙd ₒᵣdₑᵣ（如图 8（左）所示）：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L 2 n d o r d e r = ∫ Ω 4 π L ′ ( x s , − ω ) p u d ω , L_{2^{nd } order }=\int_{\Omega_{4 \pi}} L'\left(x_{s},-\omega\right) p_{u} d \omega, </math>L2ndorder=∫Ω4πL′(xs,−ω)pudω,

<math xmlns="http://www.w3.org/1998/Math/MathML"> L ′ ( x , v ) = T ( x , p ) L o ( p , v ) + ∫ t = 0 ∥ p − x ∥ σ s ( x ) T ( x , x − t v ) S ( x , ω s ) p u E I d t . \begin{aligned} L'(x, v)= & T(x, p) L_{o}(p, v)+ \\ & \int_{t=0}^{\| p-x\| } \sigma_{s}(x) T(x, x-t v) S\left(x, \omega_{s}\right) p_{u} E_{\mathcal{I}} d t . \end{aligned} </math>L′(x,v)=T(x,p)Lo(p,v)+∫t=0∥p−x∥σs(x)T(x,x−tv)S(x,ωs)puEIdt.

在方程 6 中，L' 项评估来自具有照度 Eᵢ和方向 ωₛ的单个定向光源的亮度贡献，对于与正在构建的当前查找表条目匹配的位置 xₛ。它还包含通过 Lₒ（根据反照率的漫反射响应）从地面反射的亮度贡献。L₂ₙd ₒᵣdₑᵣ应该给出到达点 xₛ的二阶散射光的亮度。但它使用 Eᵢ进行评估：它是应该作为光照度 Eᵢ的占位符。不过在这种情况下，它是一个无量纲因子 Eᵢ=1，以确保 L₂ₙd ₒᵣdₑᵣ不返回亮度值，而是作为单位为 sr⁻¹ 的传递函数，仅在后来乘以实际定向光照度时返回亮度。在方程 5 中，Lₒ也使用 Eᵢ进行评估，但为简洁起见我们省略了这一点。

其次，我们积分一个无量纲因子 fₘₛ，表示从当前着色样本位置 xₛ周围所有大气介质向其传递的能量，如下所示：

<math xmlns="http://www.w3.org/1998/Math/MathML"> f m s = ∫ Ω 4 π L f ( x s , − ω ) p u d ω , f_{m s}=\int_{\Omega_{4 \pi}} L_{f}\left(x_{s},-\omega\right) p_{u} d \omega, </math>fms=∫Ω4πLf(xs,−ω)pudω,

<math xmlns="http://www.w3.org/1998/Math/MathML"> L f ( x , v ) = ∫ t = 0 ∥ p − x ∥ σ s ( x ) T ( x , x − t v ) 1 d t . L_{f}(x, v)=\int_{t=0}^{\| p-x\| } \sigma_{s}(x) T(x, x-t v) 1 d t . </math>Lf(x,v)=∫t=0∥p−x∥σs(x)T(x,x−tv)1dt.

如图 8（右）所示。球面上的方向积分计算为 fₘₛ，其中 Lբ沿每条光线使用方程 8 积分。重要的是在此方程中跳过阴影项 S 和相位函数的采样，因为在评估 L₂ₙd ₒᵣdₑᵣ时已经考虑了它们。因此，fₘₛ是围绕 xₛ并向其积分的能量的无量纲归一化传递因子，范围在 [0,1]。为了帮助保持该范围，建议使用希莱尔 [Hil15] 提出的方程 8 积分的解析解。

如上所述，我们假设对于大于或等于 2 的散射阶数，到达 xₛ周围任何点的光与到达 xₛ本身的光相同。我们可以使用这种低空间变化假设来解析评估多次散射贡献。受双散射方法 [ZYWK08] 的启发，我们将无限多次散射光贡献因子 Fₘₛ近似为几何级数无穷和：

<math xmlns="http://www.w3.org/1998/Math/MathML"> F m s = 1 + f m s + f m s 2 + f m s 3 + . . . = 1 1 − f m s . ( 9 ) F_{m s}=1+f_{m s}+f_{m s}^{2}+f_{m s}^{3}+...=\frac{1}{1-f_{m s}} . (9) </math>Fms=1+fms+fms2+fms3+...=1−fms1.(9)

最后，具有无限多个散射阶数的定向光的总贡献可以评估为：

<math xmlns="http://www.w3.org/1998/Math/MathML"> Ψ m s = L 2 n d o r d e r F m s , ( 10 ) \Psi_{ms}=L_{2^{nd } order } F_{ms }, \quad(10) </math>Ψms=L2ndorderFms,(10)

其中二阶散射贡献 L₂ₙd ₒᵣdₑᵣ被多次散射传递函数 Fₘₛ放大。因此，传递函数 Ψₘₛ（单位 sr⁻¹）只需乘以任何定向光照度（单位为 Lux，即 cd・sr・m⁻²）即可检索像素的多次散射贡献作为亮度（cd・m⁻²）。Ψₘₛ存储在多次散射查找表中。对于大气材料设置，该查找表对于行星周围的任何视点和光方向都有效。

总之，光散射方程 3 现在可以通过我们的多次散射近似来增强，得到：

<math xmlns="http://www.w3.org/1998/Math/MathML"> L s c a t ( c , x , v ) = σ s ( x ) ∑ i = 1 N l i g h t ( T ( c , x ) S ( x , l i ) p ( v , l i ) + Ψ m s ) E i . ( 11 ) L_{scat }(c, x, v)=\sigma_{s}(x) \sum_{i=1}^{N_{light }}\left(T(c, x) S\left(x, l_{i}\right) p\left(v, l_{i}\right)+\Psi_{m s}\right) E_{i} . (11) </math>Lscat(c,x,v)=σs(x)∑i=1Nlight(T(c,x)S(x,li)p(v,li)+Ψms)Ei.(11)

这种简化避免了依赖迭代方法来评估大气中的多次散射贡献。对于我们的实时用例，fₘₛ和 L₂ₙd ₒᵣdₑᵣ在单位球面上的积分使用 64 个均匀分布的方向实现。有关更多性能细节，请参见第 7 节。

6. 结果

我们通过将我们的方法与两种最先进的技术进行比较来验证我们的大气渲染方法：Bruneton 提出的模型 [Bru17a] 和体积路径追踪器。我们比较了各种场景，并给出了每个 R、G、B 通道与基准真值路径追踪器相比的图像均方根误差（RMSE）。

我们在具有纯黑反照率的行星地形上展示结果，并且没有太阳圆盘，以免影响 RMSE 测量。此应用程序的代码是开源的 §。

首先，我们验证我们的模型能否忠实地渲染地球大气 ------ 见图 9。我们展示了仅使用单次散射的视图，以显示考虑多次散射时的差异。它还展示了三种模型：Bruneton 模型（B）、我们的模型（O）和参考路径追踪器（P）。在白天，（B）和（O）的 RSME 分别为（1.43,2.28,6.07）×10⁻³ 和（0.94,1.74,5.07）×10⁻³------ 都非常接近参考（P）。对于日落情况，值得注意的是（B）不能忠实地再现由米氏散射传播的橙色。这是因为我们使用单个 RGBA 4D 散射查找表，其中 A 表示无色米氏散射，而不是需要两个 RGB 4D 散射查找表的解决方案。这是实时应用中使用的典型设置，以分配更少的内存并提高性能（只需更新 1 个散射查找表，并且获取查找表数据需要更少的带宽）。米氏散射颜色使用 Bruneton 和 Neyret [BN08] 第 4 节中讨论的技巧恢复。还有趣的是，两种模型都能够再现地球在大气中投射的阴影中可见的淡散射颜色 ------ 见图 9 底部。

我们还比较了这些模型实现太空视图的准确性，见图 10。（B）和（O）模型都能忠实地再现地球，各自的 RSME 分别为（0.58,0.67,1.61）×10⁻³ 和（0.95,0.85,1.23）×10⁻³，以及类火星行星大气，RSME 分别为（0.87,0.97,0.94）×10⁻³ 和（1.99,0.91,0.56）×10⁻³。当涉及到具有浓密大气的艺术化小行星时，（B）模型无法高质量地再现来自行星固体核心的体积阴影。这是由于查找表参数化，导致对于具有高地表曲率的小行星缺乏准确性。通过提高 4D 光散射查找表的分辨率，可以消除模型（B）的这一限制，但会增加额外的内存和计算成本。

对于地球大气，据报道只需计算到 5 阶散射就足以捕获大部分能量 [BN08]，我们通过观察证实了这一点。然而，当让艺术家设置大气时，大气可能会变得更浓密，此时考虑更高的散射阶数就变得很重要。虽然我们的新模型（O）会自动考虑这一点，但模型（B）并非如此。在这种情况下，必须进行与需要评估的散射阶数相同次数的迭代，这很快变得不切实际，即使使用分时处理也是如此。

图 11 表明，对于更浓密的大气，更高阶的散射对于忠实地产生正确的大气颜色至关重要。我们的模型能够再现这种行为，而模型（B）无法收敛到更高散射阶数的正确颜色，甚至会出现数值爆炸（图 11（右））。这可能是由于采样查找表时的精度问题，尽管我们为模型（B）的散射查找表使用了 32 位浮点表示，而模型（O）使用 16 位浮点表示就足够了。

如图 12 所示，新模型（O）确实存在一些值得一提的问题，每个问题都源于多次散射近似：

当使用非常高的散射系数时，与基准真值相比，色调可能会丢失甚至开始偏移。
我们假设光在第二次反弹后散射方向是各向同性的。实际上这是一种近似，通过我们的模型与参考路径追踪器的比较得到证实。对于仅米氏散射，当 g=0.0 和 g=0.8 时，RMSE 分别为 0.0058 和 0.039。

7. 性能与讨论

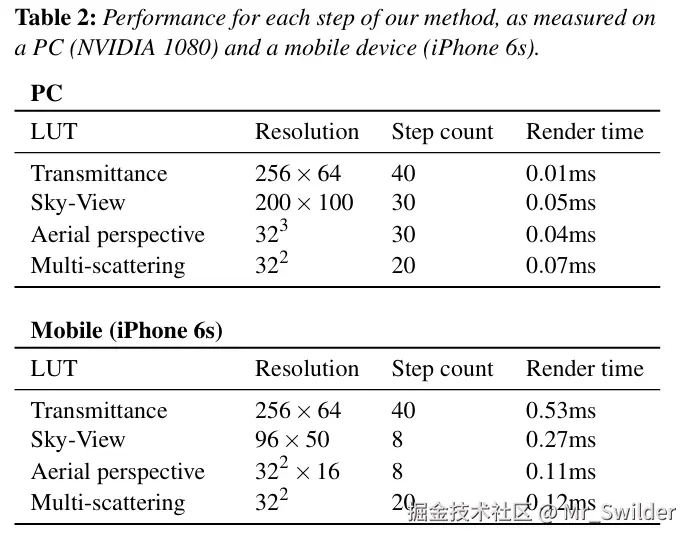
在配备 NVIDIA 1080 的 PC 上，考虑到图 9 中描绘的白天情况，最终屏幕上的天空和大气透视渲染时间为 0.14 毫秒（ms）。表 2 提供了我们方法每个步骤的更详细时间以及生成的查找表的属性。最终，1280×720 分辨率的总渲染时间为 0.31 ms。对于相同的视图，Bruneton 模型 [BN08] 的渲染时间为 0.22ms，但这是在所有查找表都未更新的情况下。使用提供的代码 [Bru17b] 更新所有查找表需要 250ms，其中 99% 的成本来自估计多次散射所需的多次迭代。如希莱尔 [Hil16] 已经表明的，可以在多个帧上分时更新。然而，当评估高散射阶数时，延迟会增加，并且需要很长时间才能在屏幕上看到结果。当从太空观察行星时，如图 10 所示，第 5.3 节中描述的天空视图查找表的准确性会降低，因为其中很大一部分被浪费在渲染空旷空间上。在这种情况下，我们无缝切换到屏幕上的简单光线步进。行星和大气的渲染时间随后会变得更昂贵（0.33ms），导致总渲染成本为 0.5ms。但这通常是可以接受的，因为行星视图聚焦于行星本身，因此渲染预算可能更高。

我们的技术可以从台式 PC 扩展到相对较旧的苹果 iPhone 6s 移动硬件。在这种情况下，可以降低查找表分辨率和样本数量，而不会对最终视觉效果产生巨大影响。表 2 说明了我们的设置和性能差异，而图 13 展示了视觉变化。由于查找表质量较低导致的视觉差异用肉眼无法察觉。请注意，我们在两个平台上都保持类似的透射率查找表，因为这对于确保匹配的外观很重要。如果可以为了性能而接受更多的视觉差异，则移动设备上的透射率查找表质量可以进一步降低。对于 Epic Games 的《堡垒之夜》，在 iPhone 6s 上的总天空渲染成本约为 1ms。

需要再现的一个重要视觉效果是体积阴影，例如从山脉到大气的阴影。由于大气不是均匀介质，因此无法使用对极采样 [BCR*10]。也无法使用阴影体方法 [BN08; Hoo16]，因为我们的查找表不允许在大气中的视图光线路径上进行这种积分采样。最后但同样重要的是，这些技术无法表示云投射的软阴影：我们必须进行光线步进。与 Valient [Val14] 和 Gjoel [GS16] 类似，我们建议使用每条光线的样本抖动和重投影来组合先前帧的样本。可以根据蓝噪声 [GS16] 进行抖动，并且可以通过时间抗锯齿（TAA）方法 [Kar14] 自动实现重投影。

如图 14 所示。使用这种方法需要与内容相关的样本数量。

在这个例子中，我们使用 32 个样本，这导致天空和大气渲染时间增加到 1.0ms。为了降低这一成本，也可以以较低分辨率进行追踪，并暂时重投影和上采样结果。一些游戏引擎已经使用了这种方法，并取得了很好的效果 [Bau19; EPI18]。带有体积阴影的结果如图 1 所示。

此外，如果第 5.5 节和图 12 中描述的近似是可接受的，我们提出的多次散射查找表还可以加速大气参与介质的路径追踪。在这种情况下，只需要对单次散射事件进行采样，例如使用 delta 跟踪 [FWKH17]。当发生此类事件时，可以立即停止追踪路径，此时使用下一个事件估计评估单次散射贡献，并使用多次散射查找表评估剩余散射阶数的贡献。当在我们的参考 GPU 路径追踪器上使用这种方法时，对于图 9 中的白天场景（路径深度为 5），720p 帧的成本从 0.74ms 降至 0.29ms。对于图 11 中的白天场景（路径深度为 50），成本从 7.9ms 降至 0.6ms。

8. 结论

总之，我们的方法可以高效地实时从多个视角渲染天空和大气，同时不断更新查找表，模拟光的多次散射，而无需进行繁琐的每散射阶数迭代计算。这对于灯光艺术家能够实现他们的构想并遵循项目的艺术指导，同时模拟时间变化和天气变化非常重要。我们已经表明，它能提供准确的视觉结果，即使由于浓密大气或强各向异性相位函数而偏离基准真值，结果仍然合理。由于它是基于物理的且能量守恒的，因此不会出现数值爆炸。此外，它可用于加速渲染天空和大气的路径追踪应用。

9. 未来工作

未来的工作可以包括研究提高各向异性相位函数查找表准确性的方法，以及支持空间变化的大气条件。我们认为在某些时候转向光谱渲染以提高方法的准确性很重要 [EK10]。最后但同样重要的是，我们认为使用路径追踪器结合去噪器实时渲染天空和大气是一个很有前景的研究方向。

致谢

我们要感谢匿名评审员的有益评论，以及 Epic Games 的整个渲染团队对论文的审阅和校对，特别是 Krzysztof Narkowicz、Charles de Rousiers、Graham Wihlidal 和 Dmitriy Dyomin。我们还要感谢 Jean-Sebastien Guay、Jordan Walker、Ryan Brucks、Sjoerd de Jong 和 Wiktor Öhman 提供的关卡艺术和对该技术的评估。最后，我们要感谢 Stephen Hill 校对论文。

参考文献

Bau19\] BAUER, FABIAN. "《荒野大镖客 2》中大气世界的创建：一个完整且集成的解决方案"。实时渲染进展，ACM SIGGRAPH 2019 课程。2019 年 2 月，9。 \[BCR\*10\] BARAN, ILYA, CHEN, JIAWEN, RAGAN-KELLEY, JONATHAN, 等。"用于单次散射的分层体积阴影算法"。ACM Trans. Graph. 29.6 (2010), 178:1--178:10 9。 \[BN08\] BRUNETON, ERIC 和 NEYRET, FABRICE. "预计算大气散射"。欧洲图形学会议论文集。2008 年，1079--1086 2--5,7--9。 \[Bou08\] BOUTHORS, ANTOINE. "云的实时逼真渲染"。博士论文。约瑟夫・傅里叶大学，2008 年。URL: http : // evasion . imag . fr / \~Antoine . Bouthors /research/phd/ 5。 \[Bru17a\] BRUNETON, ERIC. "8 种晴空模型的定性和定量评估"。IEEE 可视化与计算机图形汇刊 23.12 (2017), 2641--2655 2,3,6。 \[Bru17b\] BRUNETON, ERIC. 预计算大气散射。2017 年。URL: https : // github . com /ebruneton/precomputed _ atmospheric_scattering 2,3,8。 \[dCK17\] De CARPENTIER, GILIAM 和 KOHEI, ISHIYAMA. "Decima 引擎：光照和抗锯齿的进展"。实时渲染进展，ACM SIGGRAPH 2017 课程。纽约，NY，美国：ACM，2017 年 2 月。 \[EK10\] ELEK, OSKAR 和 KMOCH, PETR. "大规模自然参与介质中的实时光谱散射"。春季计算机图形会议（SCCG）论文集。2010 年，77--84 9。 \[Ele09\] ELEK, OSKAR. "具有多次散射的可参数化行星大气的实时渲染"。CESCG (2009) 2,3,5。 \[EPI18\] EPICGAMES. 虚幻引擎 4.19：带时间上采样的屏幕百分比。2018 年 3 月。URL: https : // docs . unrealengine . com /en - US / Engine / Rendering / ScreenPercentage/index.html 9。 \[FWKH17\] FONG, JULIAN, WRENNINGE, MAGNUS, KULLA, CHRISTOPHER, 和 HABEL, RALF. "生产级体积渲染"。ACM SIGGRAPH 2017 课程。2017 年 2,3,9。 \[GK99\] GARY E., THOMAS 和 KNUT, STAMNES. "大气和海洋中的辐射传输"。剑桥大学出版社（1999）3。 \[GS16\] GJOEL, MIKKEL 和 SVENDSEN, MIKKEL. "低复杂度，高保真 ------《Inside》渲染"。游戏开发者大会。2016 年 9 月。 \[HG13\] HOLZSCHUCH, NICOLAS 和 GASCUEL, JEAN-DOMINIQUE. "半透明材料中的双散射和多次散射效应"。IEEE 计算机图形与应用（2013），66--76 5。 \[Hil15\] HILLAIRE, SÉBASTIEN. "寒霜引擎中基于物理的统一体积渲染"。实时渲染进展，ACM SIGGRAPH 2015 课程。2015 年 6 月。 \[Hil16\] HILLAIRE, SÉBASTIEN. "寒霜引擎中基于物理的天空、大气和云渲染"。SIGGRAPH 2016 课程：基于物理的着色理论与实践。2016 年 2,4,5,8。 \[Hoo16\] HOOBLER, NATHAN. "快速、灵活、基于物理的体积光散射"。游戏开发者大会。2016 年 2,9。 \[HW12\] HOSEK, LUKAS 和 WILKIE, ALEXANDER. "全光谱天穹辐射亮度的解析模型"。ACM Trans. Graph. 31.4 (2012), 95:1--95:9 2。 \[JMLH01\] JENSEN, HENRIK WANN, MARSCHNER, STEPHEN R., LEVOY, MARC, 和 HANRAHAN, PAT. "次表面光传输的实用模型"。ACM 计算机图形与交互技术论文集。2001 年，511--518 5。 \[Kar14\] KARIS, BRIAN. "高质量时间超采样"。游戏实时渲染进展第一部分，ACM SIGGRAPH 2014 课程。2014 年，10:1--10:1 9。 \[Kut13\] KUTZ, PETER. 臭氧的重要性。2013 年。URL: [skyrenderer.blogspot.se/2013/05/the...](https://link.juejin.cn?target=http%3A%2F%2Fskyrenderer.blogspot.se%2F2013%2F05%2Fthe-importanceof-ozone.html "http://skyrenderer.blogspot.se/2013/05/the-importanceof-ozone.html") 3。 \[LdR14\] LAGARDE, SEBASTIEN 和 de ROUSIERS, CHARLES. "寒霜引擎向 PBR 的转变"。基于物理的着色理论与实践，ACM SIGGRAPH 2014 课程。2014 年 2 月。 \[NAS\] NASA. 地球概况表。URL: https : // nssdc . gsfc . nasa.gov/planetary/factsheet/earthfact.html 3。 \[NDN96\] NISHITA, TOMOYUKI, DOBASHI, YOSHINORI, 和 NAKAMAE, EIHACHIRO. "考虑多次各向异性散射和天光的云显示"。ACM 计算机图形与交互技术论文集。1996 年，379--386 2。 \[NSJ\] NOVÁK, JAN, SELLE, ANDREW, 和 JAROSZ, WOJCIECH. "用于估计参与介质中衰减的残余比率跟踪"。ACM Trans. Graph. 33.6 (), 179:1--179:11 3。 \[NSTN93\] NISHITA, TOMOYUKI, SIRAI, TAKAO, TADAMURA, KATSUMI, 和 NAKAMAE, EIHACHIRO. "考虑大气散射的地球显示"。ACM 计算机图形与交互技术论文集。1993 年，175--182 2。 \[ONe07\] O'NEIL, SEAN. "精确的大气散射"。GPU Gems 2。2007 年 2 月。 \[PSS99\] PREETHAM, A. J., SHIRLEY, PETER, 和 SMITS, BRIAN. "实用的日光解析模型"。ACM 计算机图形与交互技术论文集。1999 年，91--100 2。 \[Val14\] VALIENT, MICHAL. "《杀戮地带：暗影坠落》的下一代图像质量"。游戏开发者大会。2014 年 9 月。 \[Wen07\] WENZEL, CARSTEN. "游戏中的实时大气效果再探讨"。游戏开发者大会。2007 年 2 月。 \[Yan97\] YANOVITSKIJ, EDGARD G. 非均匀大气中的光散射。施普林格出版社柏林海德堡，1997 年 5 月。 \[Yus13\] YUSOV, EGOR. "室外光散射"。游戏开发者大会。2013 年 2,5。 \[ZYWK08\] ZINKE, ARNO, YUKSEL, CEM, WEBER, ANDREAS, 和 KEYSER, JOHN. "头发中快速多次散射的双散射近似"。ACM Trans. Graph. 27.3 (2008), 32:1--32:10 5,6。 © 2020 作者 (s) 计算机图形论坛 © 2020 欧洲图形学协会和约翰・威利父子有限公司。