最短路
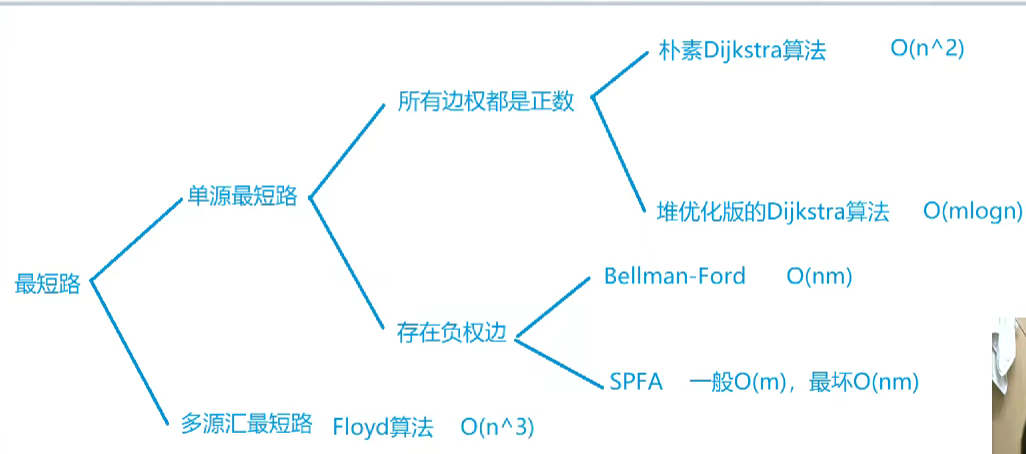
单源最短路
朴素dijkstra
时间复杂度O(n^2),适用于稠密图,所以用邻接矩阵存储
cpp
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=510;
int n,m;
int g[N][N];
int dist[N];
bool st[N];
int dijkstra(){
memset(dist,0x3f,sizeof(dist));
dist[1] = 0;
for(int i=0;i<n;i++){
int t=-1;
for(int j=1;j<=n;j++){
if(!st[j] && (t==-1||dist[t]>dist[j]))
t = j;
}
st[t]=true;
for (int j = 1;j<=n;j++)
dist[j] = min(dist[j], dist[t] + g[t][j]);
}
if(dist[n]==0x3f3f3f) return -1;
return dist[n];
}
int main(){
scanf("%d%d",&n,&m);
memset(g,0x3f,sizeof(g));
while(m--){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
g[a][b] = min(g[a][b], c);
}
int t=dijkstra();
printf("%d\n", t);
}堆优化dijkstra
时间复杂度m*logn
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
typedef pair<int, int> PII;
int n, m;
vector<PII> edge[N];
int dist[N];
bool st[N];
int dijkstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
priority_queue<PII, vector<PII>, greater<PII>> heap;
heap.push({0, 1});
while (heap.size())
{
auto t = heap.top();
heap.pop();
int ver = t.second;
if (st[ver])
continue;
st[ver] = true;
for (auto k : edge[ver])
{
int to = k.first;
int w = k.second;
if (dist[to] > dist[ver] + w)
{
dist[to] = dist[ver] + w;
heap.push({dist[to], to});
}
}
}
if (dist[n] == 0x3f3f3f3f)
return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
while (m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edge[a].push_back({b, c});
}
int t = dijkstra();
printf("%d\n", t);
}
/*
3 3
1 2 2
2 3 1
1 3 4
输出
3
*/朴素bellman_ford
时间复杂度:O(nm)
k是经过多少条边,该算法可以求一点点经过多少条边到另外一点的最短路径
求1到n的最短路径,k为n-1
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 510, M = 10010;
int n,m,k;
int dist[N],backup[N];
struct Edge{
int a, b, w;
}edges[M];
int bellman_ford(){
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
for(int i=0;i<k;i++){
memcpy(backup,dist,sizeof(dist));
for (int j = 0;j<m;j++){
int a = edges[j].a, b = edges[j].b, w = edges[j].w;
dist[b] = min(dist[b], backup[a] + w);
}
}
if(dist[n]>0x3f3f3f3f/2) return -1; //防止∞+(-10) 更新∞
return dist[n];
}
int main(){
scanf("%d%d%d",&n,&m,&k);
for (int i = 0; i < m;i++){
int a,b,w;
scanf("%d%d%d", &a, &b, &w);
edges[i] = {a, b, w};
}
int t=bellman_ford();
printf("%d", t);
}
/*
3 3 1
1 2 1
2 3 1
1 3 3
输出
3
*/优化spfa
限制:图中有负环
时间复杂度一般O(m),最坏O(nm)
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
typedef pair<int, int> PII;
int n, m;
vector<PII> edge[N];
int dist[N];
bool st[N];
int spfa()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0;
queue<int> q;
q.push(1);
st[1]=true;
while(q.size()){
int t=q.front();
q.pop();
st[t]=false;
for (auto k:edge[t]){
int to=k.first,w=k.second;
if(dist[to] > dist[t] + w){
dist[to] = dist[t] + w;
if(!st[to]){
q.push(to);
st[to] = true;
}
}
}
}
if (dist[n] == 0x3f3f3f3f)
return -1;
return dist[n];
}
int main()
{
scanf("%d%d", &n, &m);
while (m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edge[a].push_back({b, c});
}
int t = spfa();
printf("%d\n", t);
}
/*
3 3
1 2 2
2 3 1
1 3 4
输出
3
*/spfa检测负环
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 100010;
typedef pair<int, int> PII;
int n, m;
vector<PII> edge[N];
int dist[N],cnt[N];
bool st[N];
int spfa()
{
queue<int> q;
for (int i = 1;i<=n;i++){
st[i]=true;
q.push(i);
}
while (q.size())
{
int t = q.front();
q.pop();
st[t] = false;
for (auto k : edge[t])
{
int to = k.first, w = k.second;
if (dist[to] > dist[t] + w)
{
dist[to] = dist[t] + w;
cnt[to] = cnt[t] + 1;
if(cnt[to] >= n) return true;
if (!st[to])
{
q.push(to);
st[to] = true;
}
}
}
}
return false;
}
int main()
{
scanf("%d%d", &n, &m);
while (m--)
{
int a, b, c;
scanf("%d%d%d", &a, &b, &c);
edge[a].push_back({b, c});
}
if(spfa()) puts("yes");
else puts("no");
}
/*
3 3
1 2 -1
2 3 4
3 1 -4
输出
yes
*/多源最短路
Floyd
cpp
#include<bits/stdc++.h>
using namespace std;
const int N = 210, INF = 1e9;
int n,m,Q;
int d[N][N];
void floyd(){
for (int k = 1; k <= n;k++){
for(int i=1;i<=n;i++){
for (int j = 1;j<=n;j++){
d[i][j] = min(d[i][j], d[i][k] + d[k][j]);
}
}
}
}
int main(){
scanf("%d%d%d",&n,&m,&Q);
for (int i = 1; i <= n;i++){
for (int j = 1;j<=n;j++){
if(i==j) d[i][j]=0;
else d[i][j]=INF;
}
}
while(m--){
int a,b,w;
scanf("%d%d%d",&a,&b,&w);
d[a][b] = min(d[a][b], w);//重边
}
floyd();
while(Q--){
int a,b;
scanf("%d%d",&a,&b);
if(d[a][b]>INF/2) puts("impossible");
else printf("%d\n", d[a][b]);
}
return 0;
}
/*
3 3 2
1 2 1
2 3 2
1 3 1
2 1
1 3
输出
impossible
1
*/