文章目录
神经网络(多层感知机)(第二课第二周)
一、回顾我们使用tensorflow拟合训练一个手写数字的神经网络
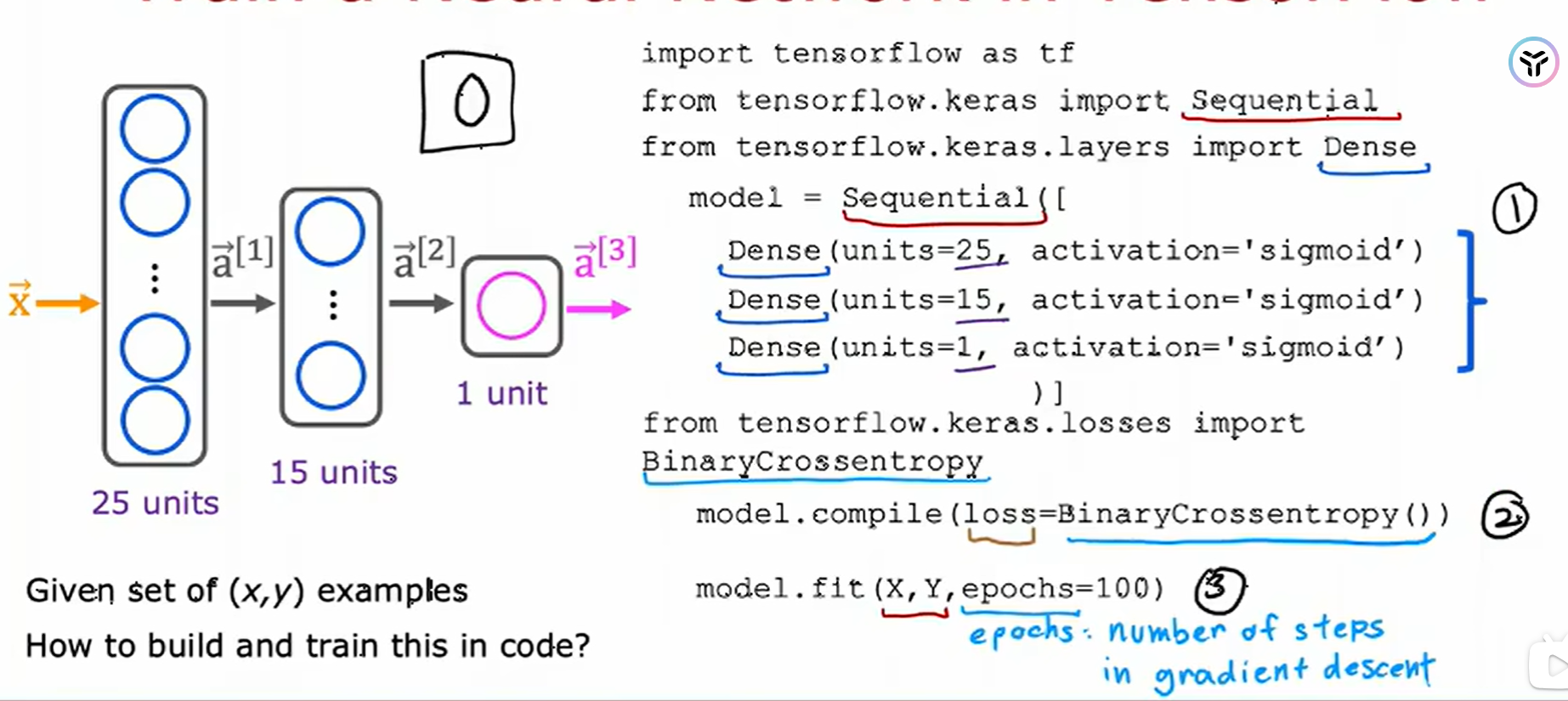
根据上面的图片我们可以知道,训练这个神经网络的步骤大致有三步:
1、指定模型,告诉tensorflow如何进行推理计算;
2、使用特定的损失函数编译模型;
3、训练模型。
二、上述代码具体的实现细节是什么?

特别要注意的是在第一步中,指定损失函数时,我们是以数字识别数据集(MNIST)为示例,这个数据集常用的损失函数是二元交叉熵,也就是我们逻辑回归中使用的损失函数。
三、激活函数的选择与使用
下面是一些神经网络中最常见的激活函数:还有第四种激活函数叫做Softmax。
通常当我们正解决二分类问题时,输出是0或者1;我们可以使用sigmoid函数;如果是解决回归问题,输出是任意的实数,建议使用线性激活函数(第一种);另外如果我们想要预测的值是一个非负数(例如预测房价),建议使用ReLu激活函数(第三种)。
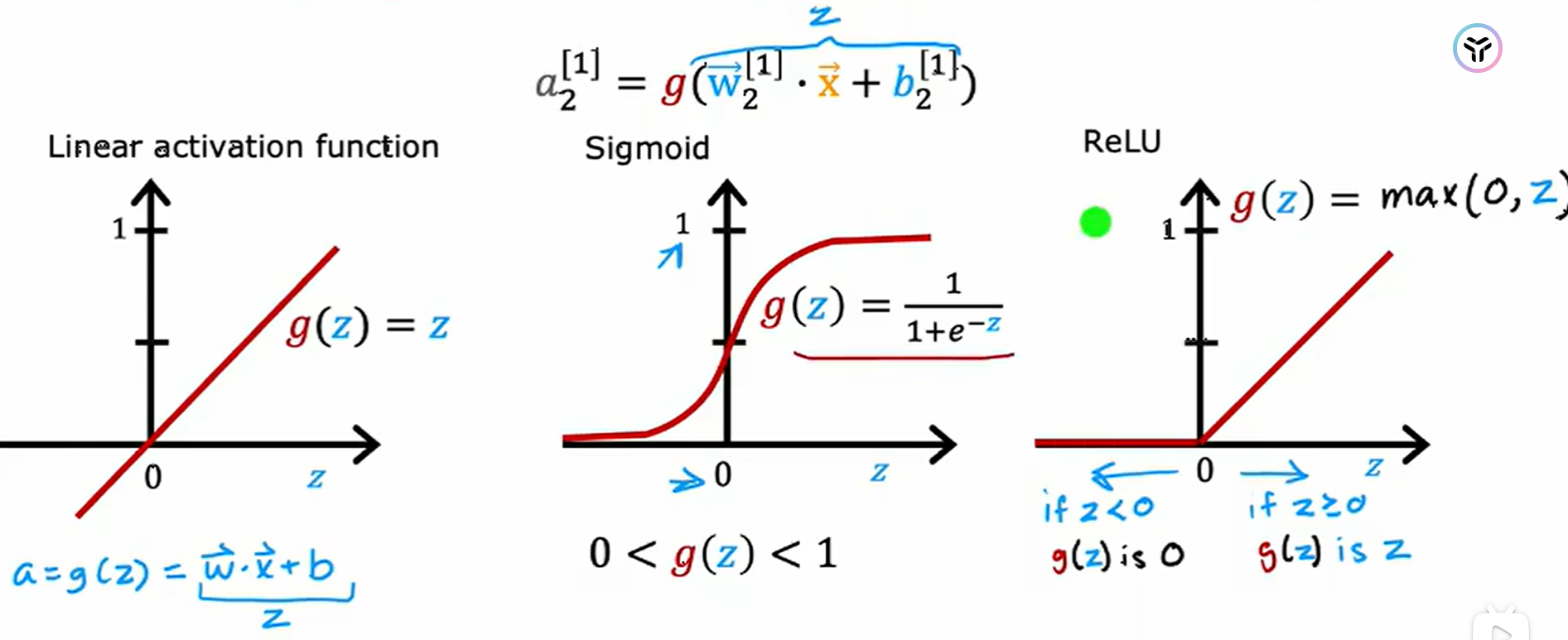
在隐藏层,我们默认使用ReLu激活函数。为啥呢?请看下面这句话。
ReLU 激活的"关闭"或禁用功能使模型能够将线性段拼接在一起,以对复杂的非线性函数进行建模。
四、为什么要使用激活函数?
当我们将所有的隐藏层都使用线性激活函数时,模型还不如直接使用单个的线性回归。这样的神经网络学习不到比线性回归更深层次的东西。这个模型计算的输出完全等同于线性回归。
同理,当所有的隐藏层都使用线性激活函数,输出层使用sigmoid激活函数,这样的神经网络就等同于逻辑回归。
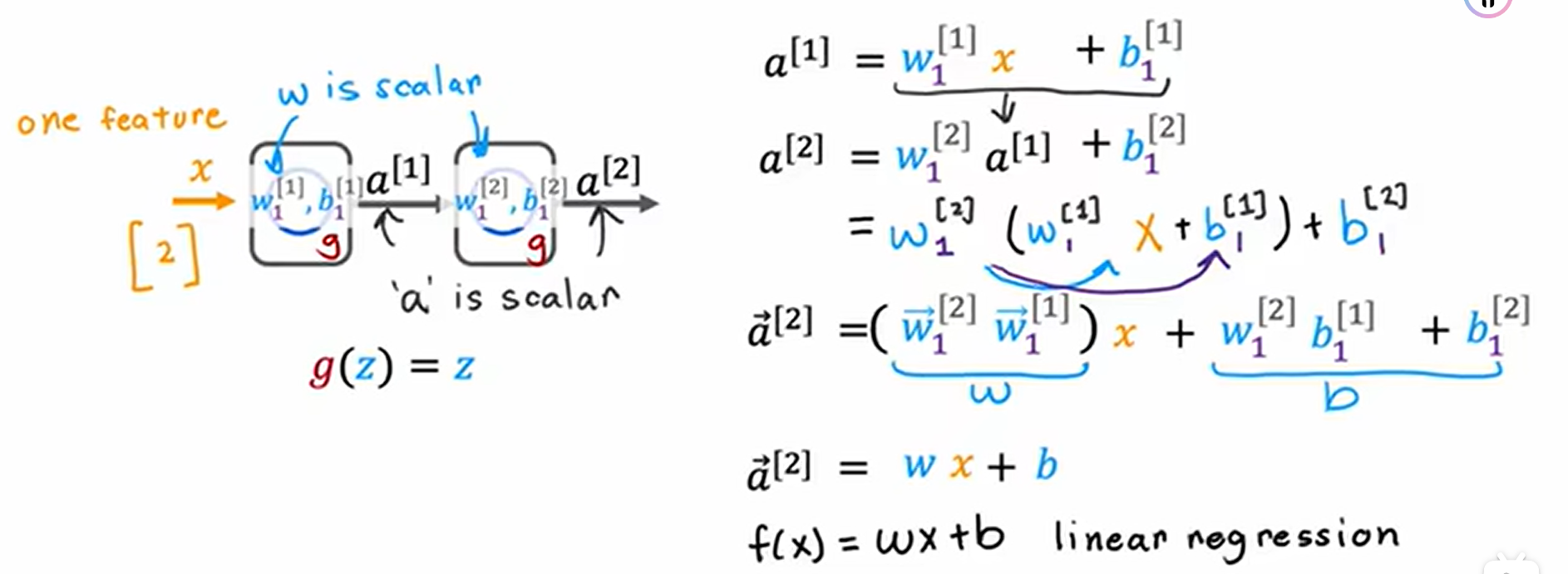
五、多分类问题,当输出的值不再是0或者1,可能的输出的值有几个或者几十个
1、一般的逻辑回归与Softmax回归的比较:
Softmax回归算法用于解决多分类问题,是逻辑回归的一种拓展。

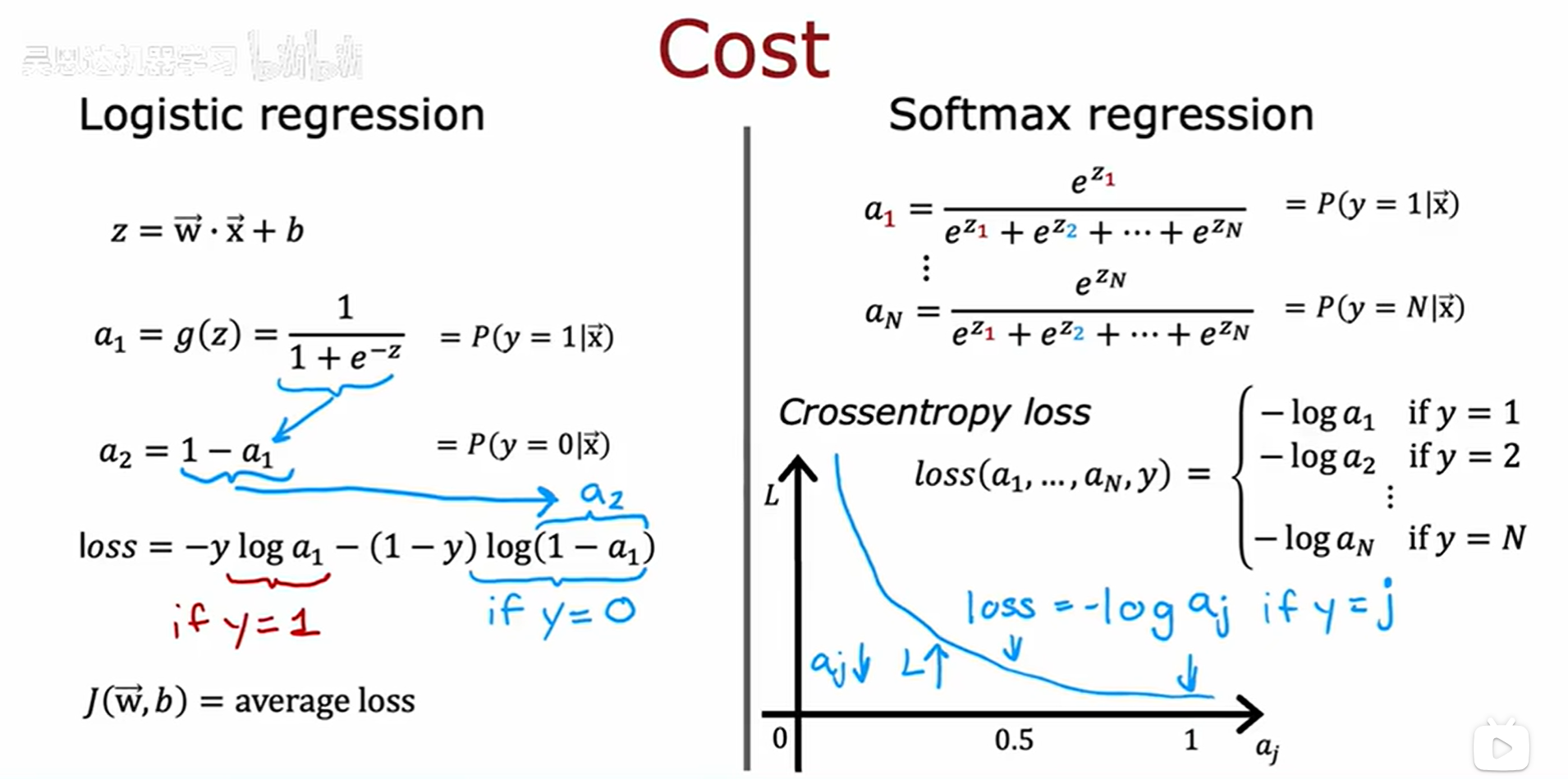
2、成本函数比较:
事实上,这两者的损失函数可以进行相互转化。
3、将Softmax回归应用到神经网络中去
主要修改神经网络的输出层: 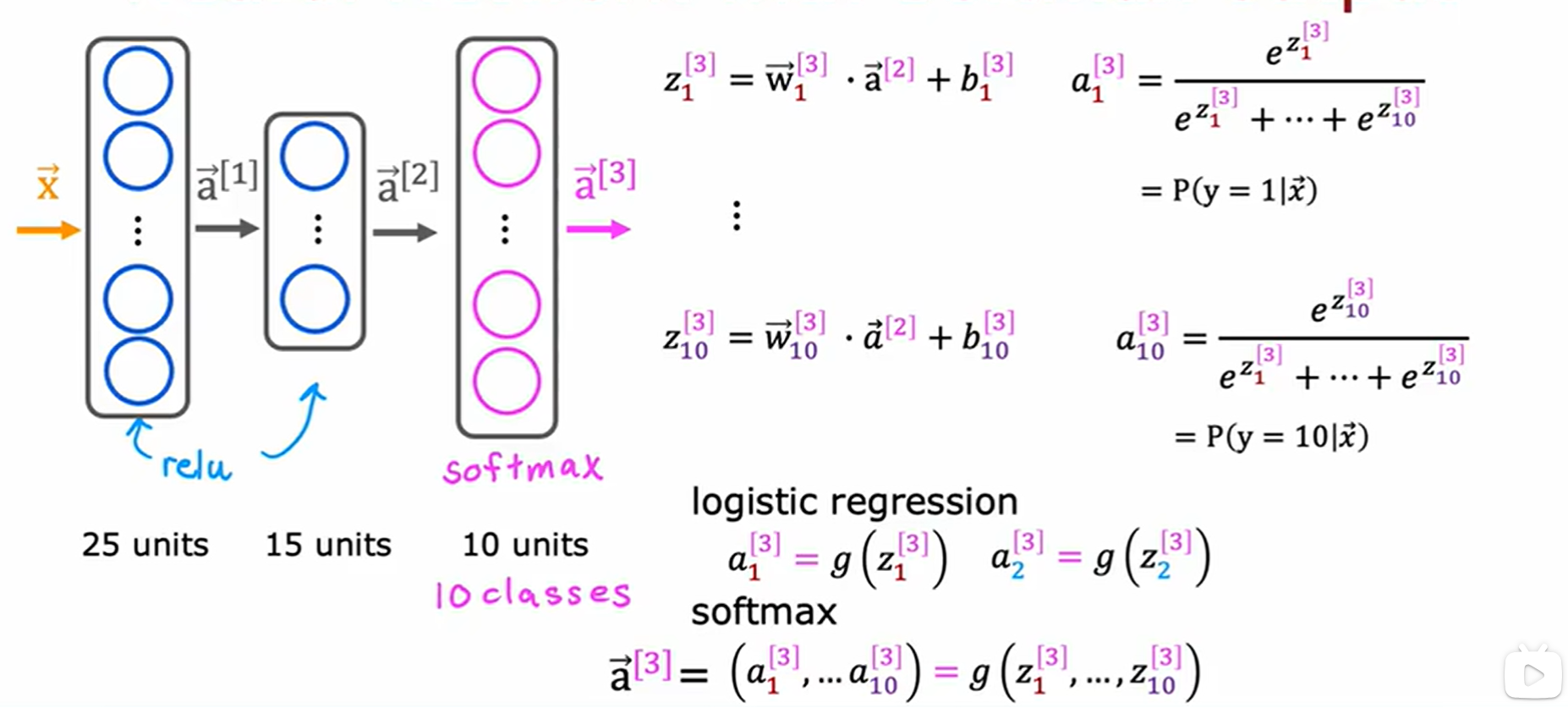
如何使用tensorflow实现这个呢?下面只是一个示例代码,之后会有更好的代码版本,其中使用的损失函数是:稀疏多分类交叉熵损失函数。

在输出层为sigmoid激活函数或者softmax激活函数时,我们可以修改输出层激活函数和计算损失函数的代码来减少数值舍入误差。示例如下:
(第一个示例的损失函数的选择存在一定问题,大家先看第二个)。


通过上面的修改之后,模型最终输出的是z值,而不是a值,还需要我们进一步转换,两种情况的示例如下:
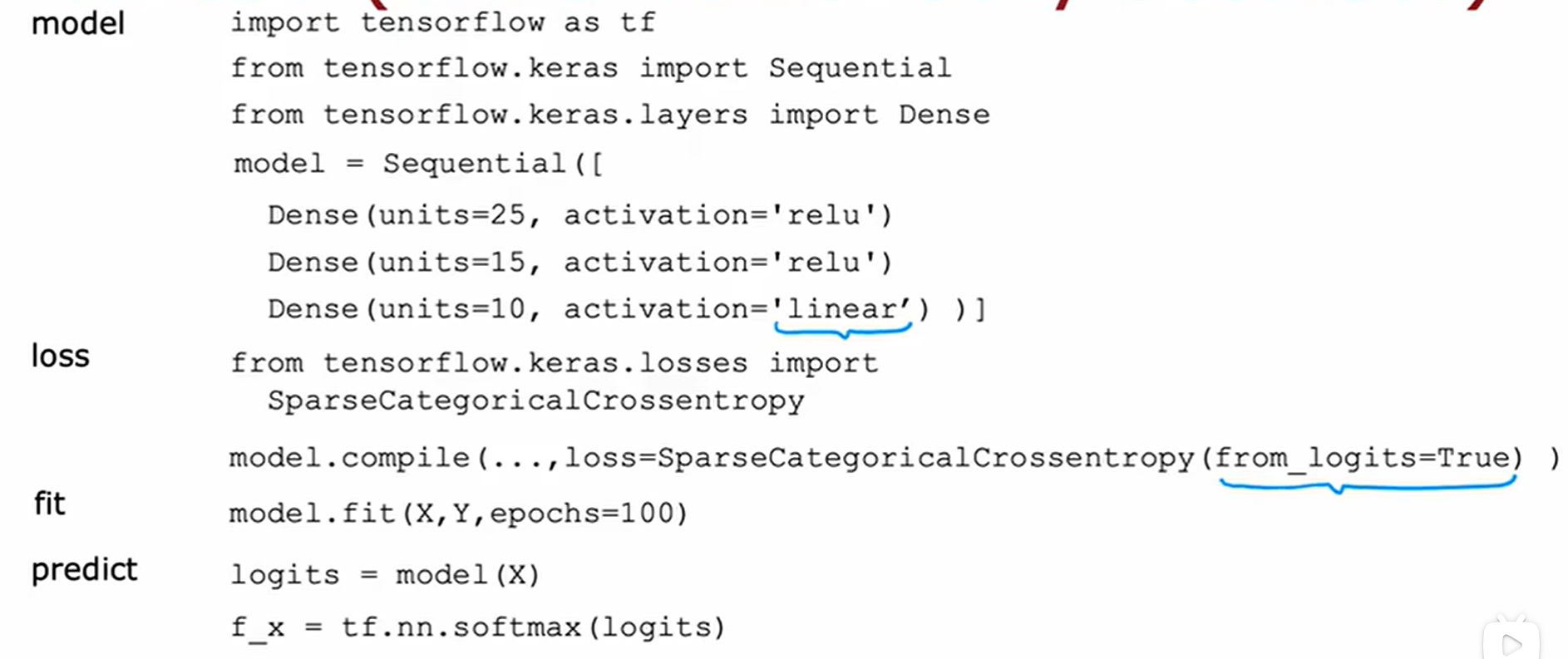
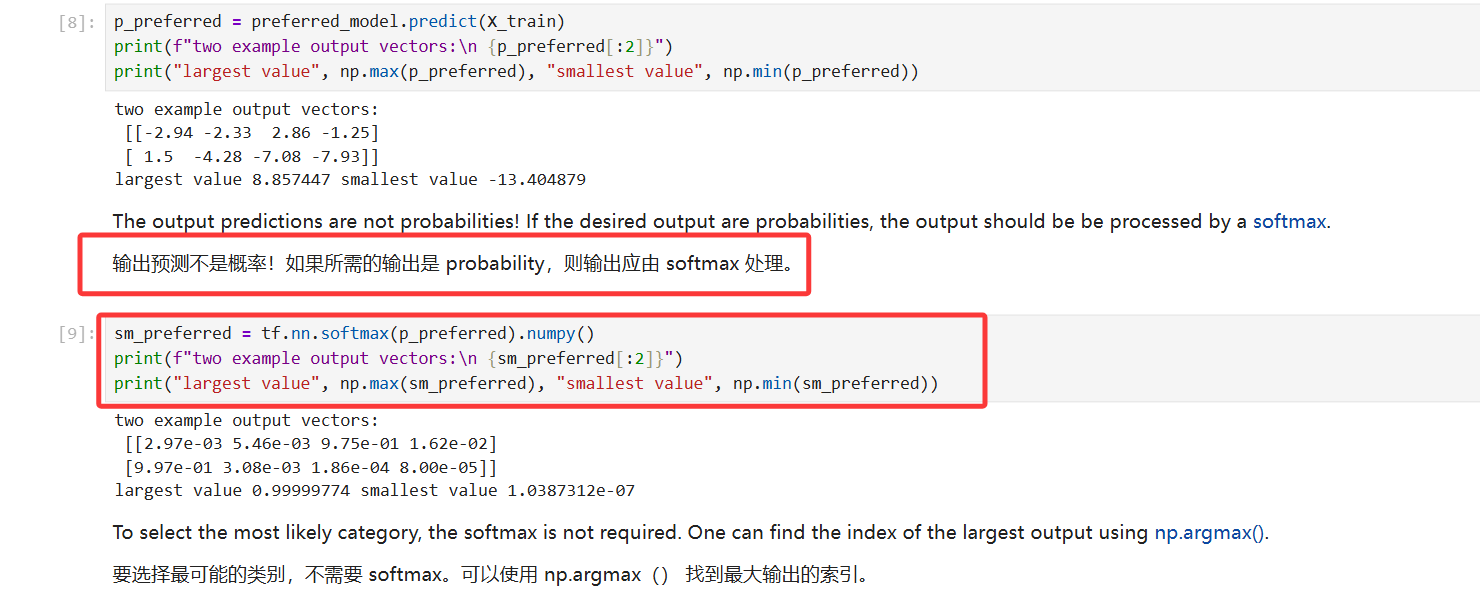
经过上述修改之后,具体的输出我们还要怎么处理呢?
1、模型定义如下: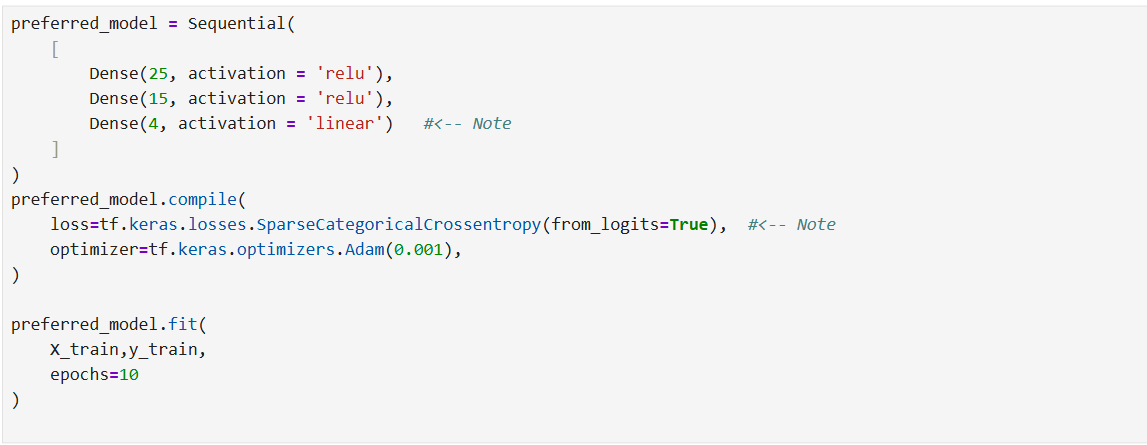
补充说明:Adam算法是模型在梯度下降过程中动态地调整学习率,以实现更快地梯度下降,避免无效步骤。
2、输出处理如下:

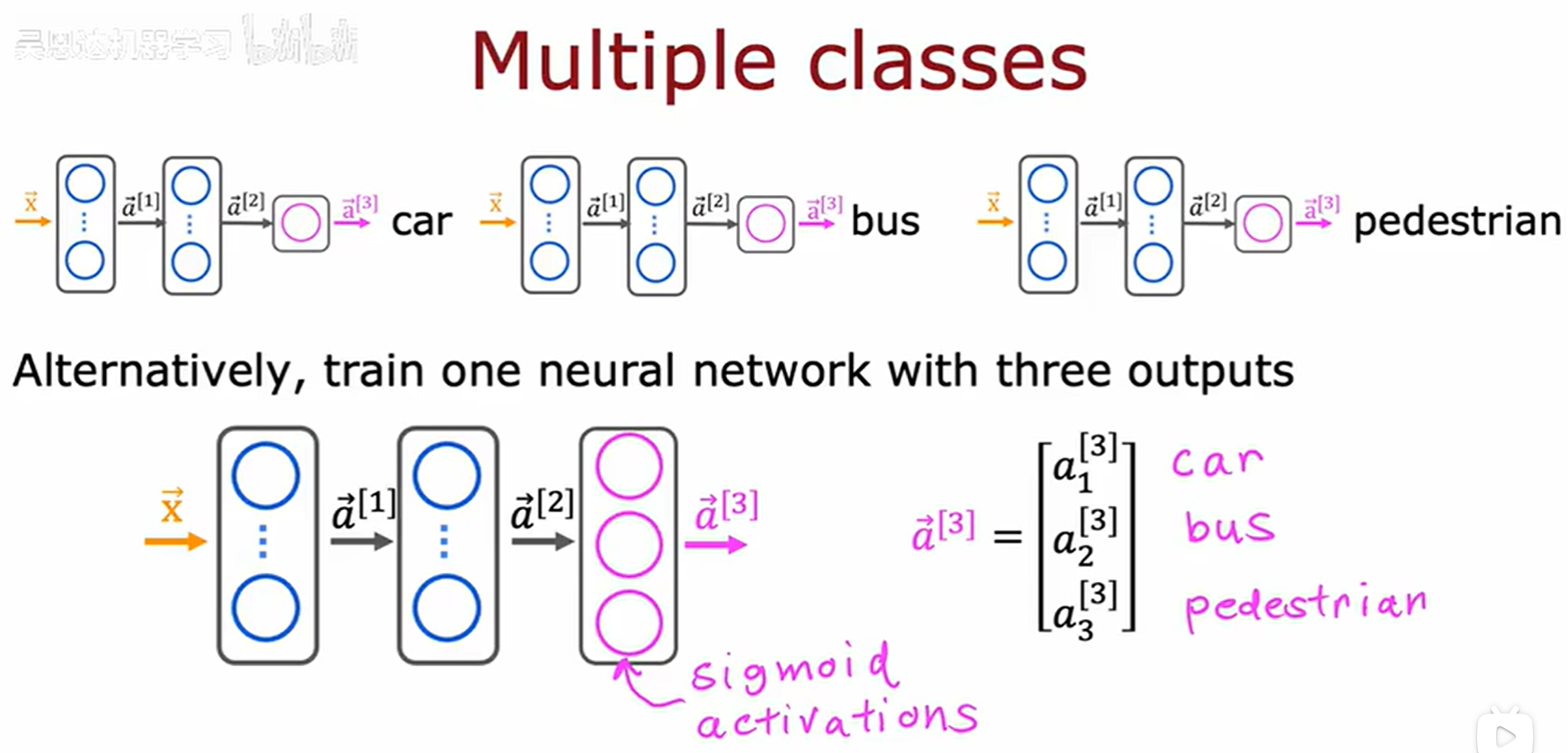
六、多标签分类问题
针对多标签分类问题,我们可以建立多个二分类神经网络模型来依次检测,同时也可以建立一个大的神经网络来同时检测这三个二分类问题。示例如下:
七、卷积神经网络
我们之前提到地神经网络都是密集层,上一层的输出全部作为下一层的输入。而卷积神经网络中每一层中的某个激活值可能只需要上一层的某几个激活值。
示例如下:(以心电图数据为例)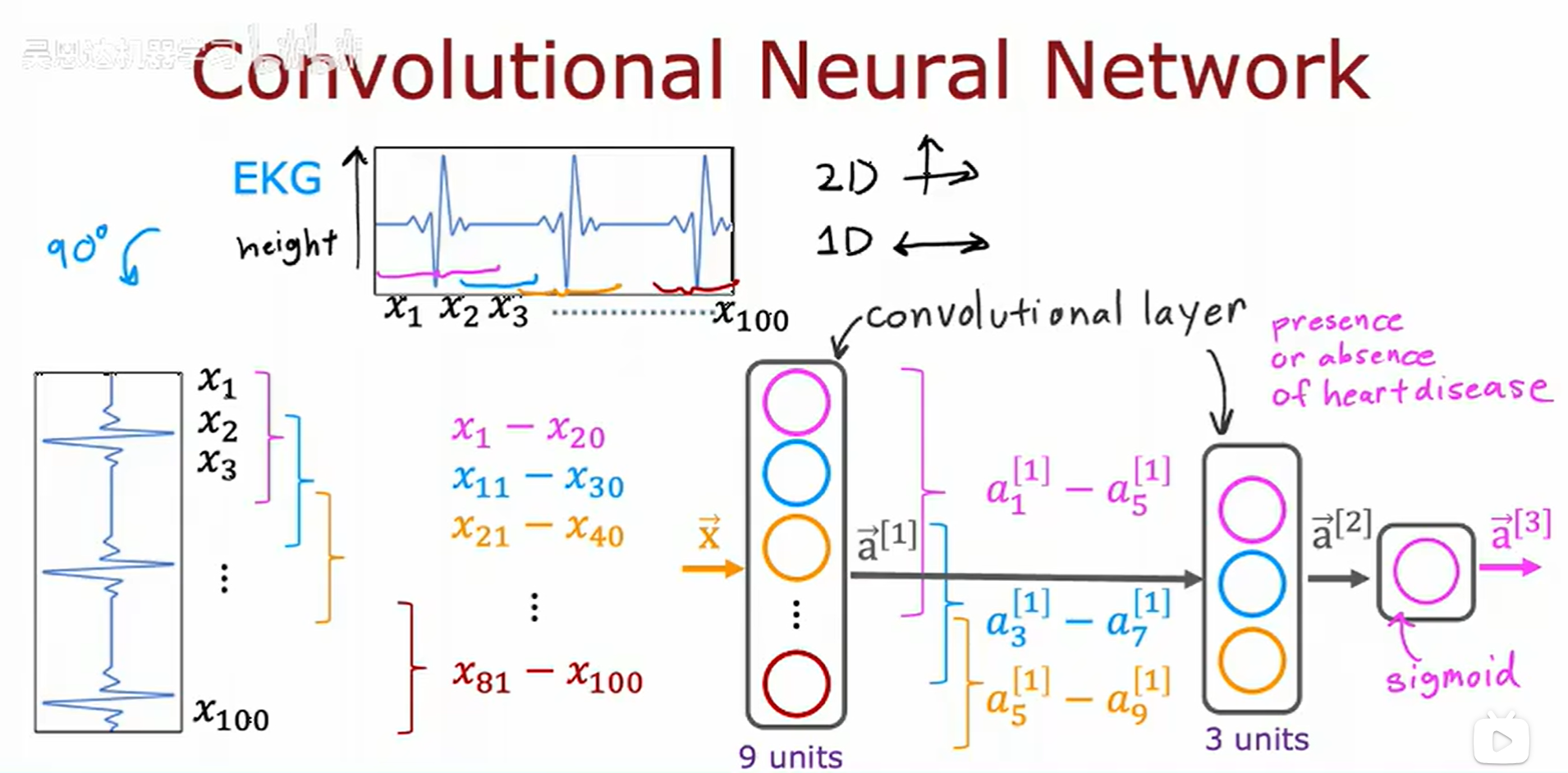
课后练习请看这一个:(配套代码中)