精密全波整流电路(四)
背景说明
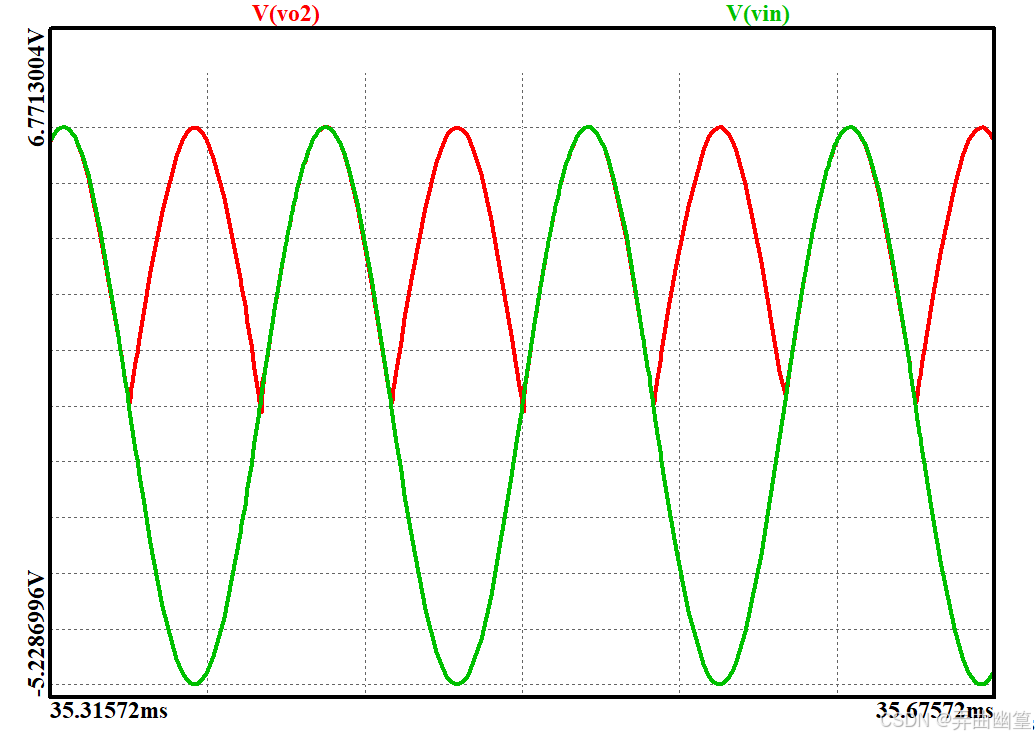
\[精密半波整流电路\|半波整流\]\]虽然能实现交直流信号的转换,但是半波整流只能保留信号半个周期的能量,导致信号能量的利用率不高。 因此,在一些场合需要使用到全波整流电路。 同样的,普通的桥式全波整流电路由于二极管压降的存在,导致整流后信号的幅值不准确。 因此,同样需要引入运放。 相比半波整流,全波整流的方案就比较多了,就收集和仿真分析了几种常见的。 以下是关于精密全波整流所有电路仿真的目录: * [精密全波整流电路(一)经典电路](https://blog.csdn.net/juxiandesiyu/article/details/149548607?spm=1001.2014.3001.5501) * [精密全波整流电路(二)四二极管电路](https://blog.csdn.net/juxiandesiyu/article/details/149548714?spm=1001.2014.3001.5502) * [精密全波整流电路(三)高输入阻抗电路](https://blog.csdn.net/juxiandesiyu/article/details/149601387?spm=1011.2415.3001.5331) * [精密全波整流电路(四)TI方案](https://blog.csdn.net/juxiandesiyu/article/details/149671963?spm=1001.2014.3001.5502) ### TI方案 在TI的《模拟工程师电路设计手册》中给出如下电路,相较于前面三个电路,这个电路使用的元器件数量更少,网络看起来也更加的简洁。 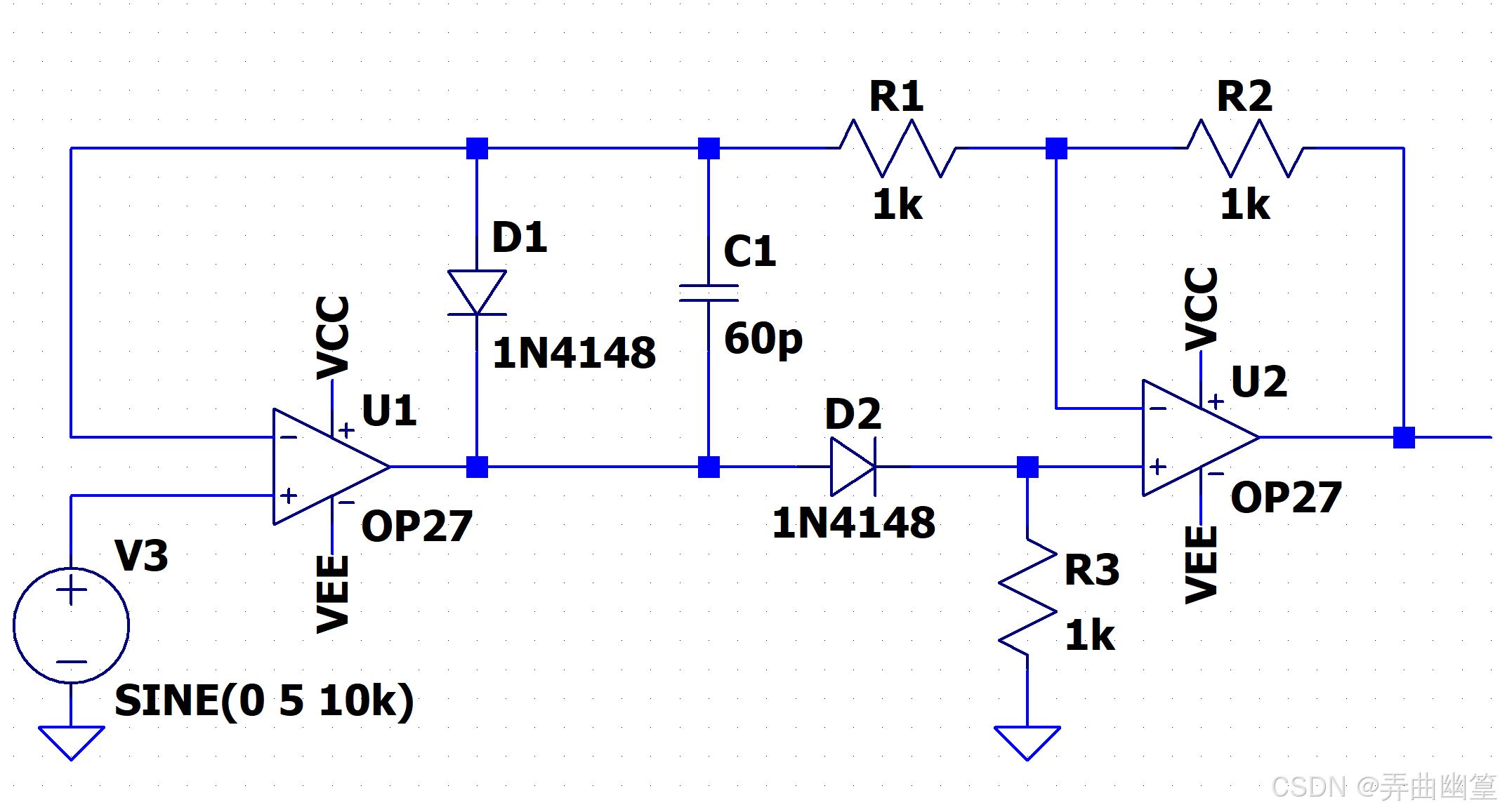 ### 原理说明 当 V i n \> 0 V_{in}\>0 Vin\>0时, D 1 D_{1} D1截止, D 2 D_{2} D2导通,该电路可以等效为: 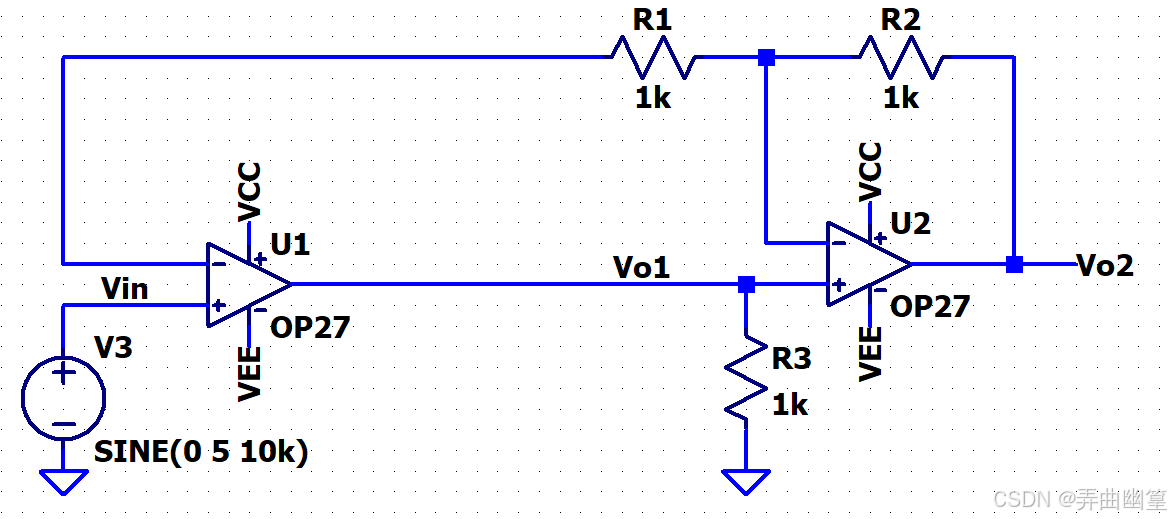 在这个电路中,由于"虚短"原则,所以运放U1的反相输入端的电压 V 1 − = V i n V_{1-}=V_{in} V1−=Vin。 同时,又因为"虚短"原则,电阻 R 1 R_{1} R1和 R 2 R_{2} R2上的电流为零,所以显然就有 V o 2 = V i n V_{o2}=V_{in} Vo2=Vin。 当 V i n \> 0 V_{in}\>0 Vin\>0时, D 1 D_{1} D1导通, D 2 D_{2} D2截止,该电路可以等效为: 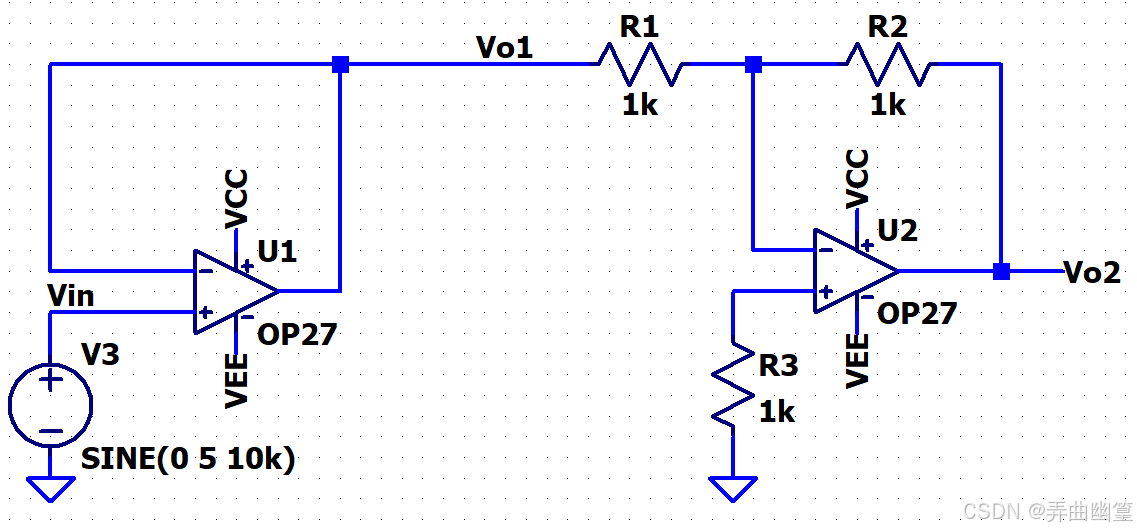 此时,整个电路相当于一个电压跟随器串接一个反相放大器,可以很轻易地写出此时电路的传递函数: V o 2 = − R 2 R 1 V i n V_{o2}=-\\frac{R_{2}}{R_{1}}V_{in} Vo2=−R1R2Vin ### 设计说明 * 在电路中电容C1起到相位补偿的作用,防止电路震荡,根据运放的不同可以选取不同大小的电容,电容不能太小,否则失去补偿作用。也不能过大,否则会导致信号在转换边沿产生较大的失真。 * 电阻 R 1 R_{1} R1和 R 2 R_{2} R2的匹配程度决定着电路的精度,尽量选用高精度的电阻。阻值也不应过大,防止出现过大的电阻噪声。 ### 仿真结果 #### 直流分析 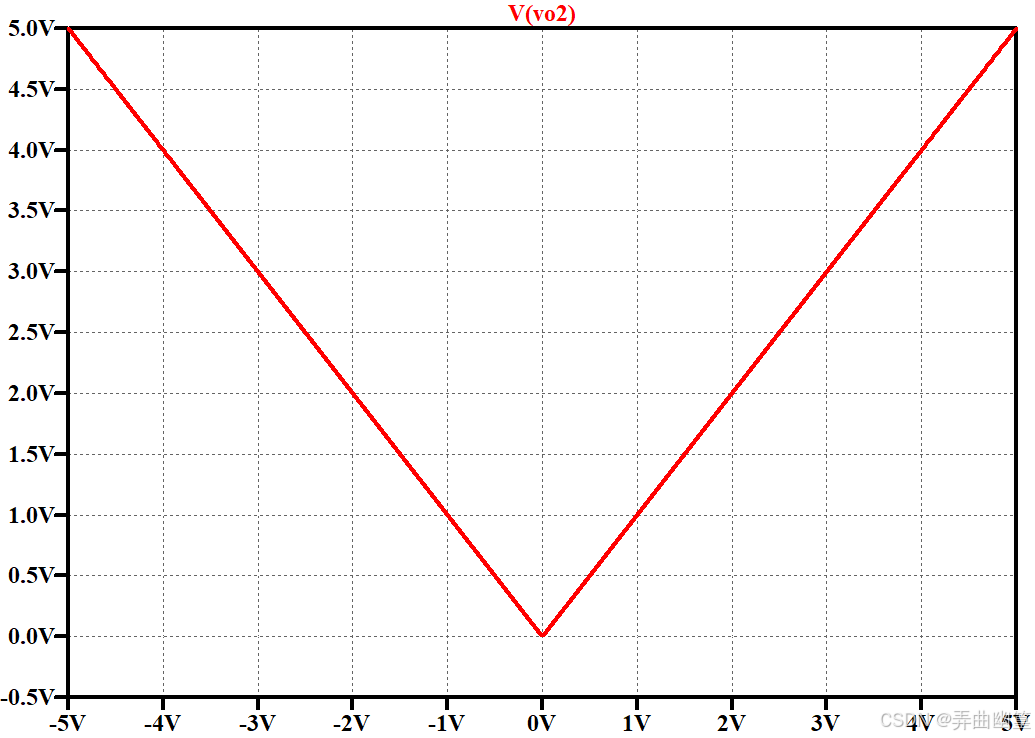 #### 交流分析 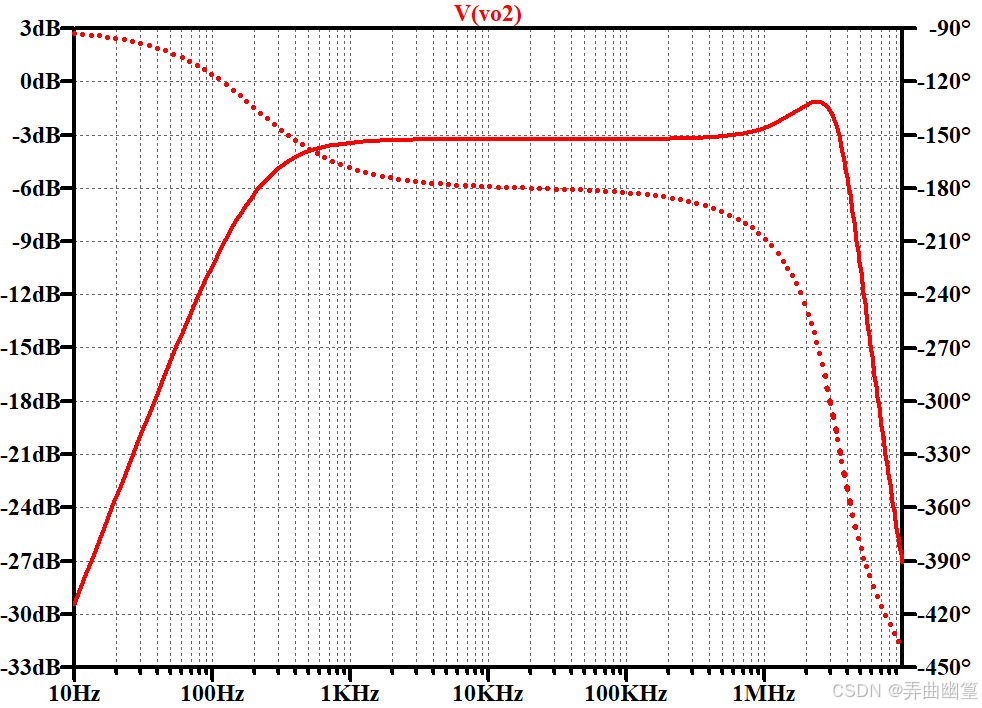 #### 瞬态分析