现有一个容量为10GB的磁盘分区,磁盘空间以簇(Cluster)为单位进行分配,簇的大小为4KB,若采用位图法管理该分区的空闲空间,即用一位(bit)标识一个簇是否被分配,则存放该位图所需簇的个数为( )
A.80 B.320 C.80K D.320K
可以先列个表方便我们加深理解:
|--------------|-----------|---------|---------------------------|---------------------------------|-----------------------------|---|------------------------------|---|
| | 1G=1024MB | | 1MB=1024KB(千字节) | | 1KB=1024Byte(字节,Byte也可简写为B) | | 1byte=8bit (比特位,bit也可简说为"位") | |
| 容量为10GB的磁盘分区 | 转换为→ | 10240MB | 转换为→ | 10485760KB | | → | | |
| | | | | ⬇ | | | | |
| | | | | 磁盘空间以簇(Cluster)为单位进行分配,簇的大小为4KB | | | | |
| | | | 以簇(Cluster)为单位进行分配后的磁盘容量→ | 2621440KB | | | | |
因为采用位图法管理该分区的空闲空间,即用一位(bit)标识一个簇是否被分配,
用下图来表示我的想法,我将其称之为"低级上位画图法",
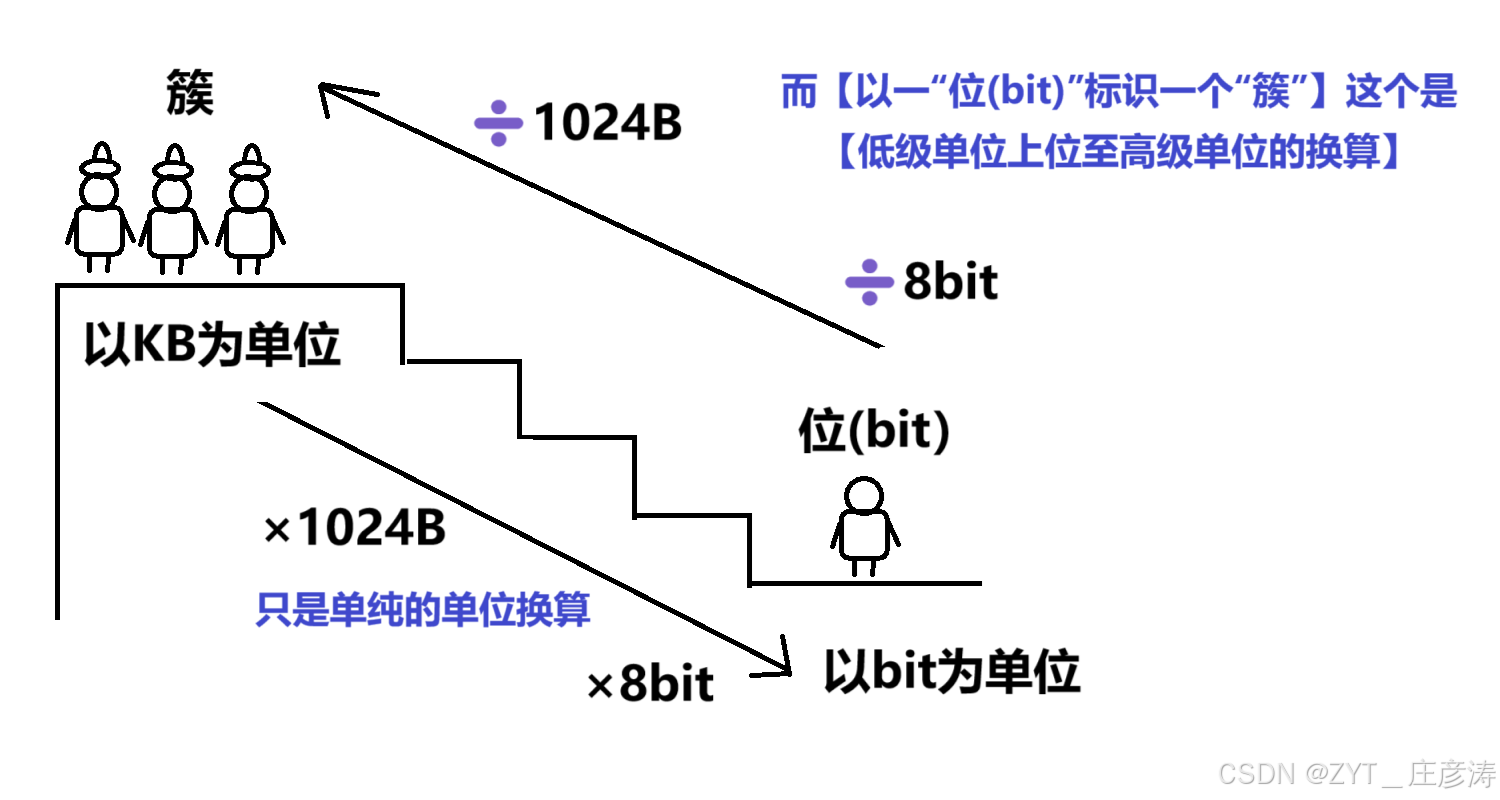
你看,一般以"簇"为单位要转换成以"位(bit)"为单位来计算,就必须乘1024B再乘8bit才行,这是简单的【单位之间的换算】。
而要让"位(bit)"来标识一个"簇"是否被分配,
这句话是针对【低级单位上位至高级单位的换算】来讲的。
也就是让本来级别比"簇"低的"位(bit)"加入"簇"的队伍,即让"位(bit)"来站在"簇"的位置上对磁盘容量进行单位计算,欲戴其冠必承其重,就必须拿【以簇(Cluster)为单位进行分配后的磁盘容量】除以回去,除以8bit得到的数再除以1024B,这样才能转换为【以一"位(bit)"标识一个"簇"】进行分配后的磁盘容量
因为刚才表格中计算出来的【以簇(Cluster)为单位进行分配后的磁盘容量】为2621440KB,所以
故转换为【以一"位(bit)"标识一个"簇"】进行分配后的磁盘容量为:
2621440KB÷8bit÷1024B=320KB。
这个得出来的磁盘容量除以【簇的大小为4KB】即320KB÷4KB就等于存放该位图所需簇的个数,即80个。