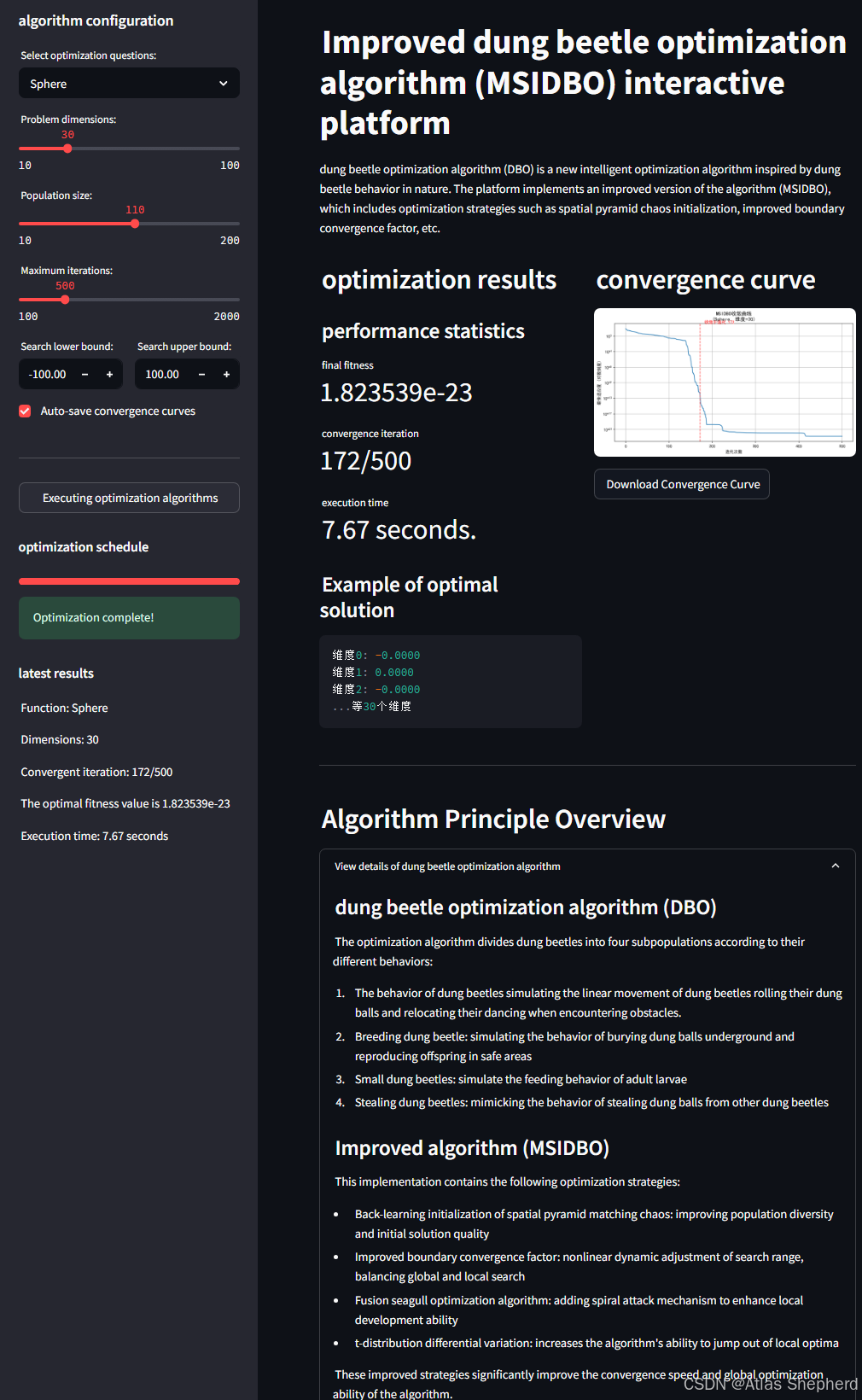
蜣螂优化算法的华丽转身：基于Streamlit的MSIDBO算法可视化平台

2301_764441332025-07-29 14:25

基于Streamlit的交互式Web应用，用于展示和运行改进的蜣螂优化算法（MSIDBO）。以下是代码的详细解读，分模块说明其功能和实现细节：

1. 算法核心：MSIDBO类（未完整展示）

虽然代码中未完整展示MSIDBO类的实现，但通过run_optimization函数的调用可以推断其结构：

  • MSIDBO类定义：包含算法的核心逻辑，如种群初始化、迭代优化、收敛判断等。
  • 关键方法 ：
    • __init__: 初始化参数（目标函数、维度、搜索边界、种群大小、最大迭代次数等）。
    • run: 执行优化过程，返回最优解（best_solution）、最优适应值（best_fitness）和收敛历史（history）。
  • 算法改进点 （根据代码注释）：
    • 空间金字塔混沌初始化：提高种群多样性。
    • 改进边界收敛因子：动态调整搜索范围，平衡全局与局部搜索。
    • 融合海鸥优化的螺旋攻击机制：增强局部开发能力。
    • t-分布差分变异：增加跳出局部最优的能力。

2. Streamlit Web应用结构

代码使用Streamlit构建交互式界面，分为以下几个模块：

(1) 页面配置
复制代码 
st.set_page_config( page_title="🐞 改进蜣螂优化算法平台", page_icon="🐞", layout="wide" )
  • 设置页面标题、图标和布局为宽屏模式。
(2) 侧边栏配置
  • 问题选择：通过下拉菜单选择优化目标函数（如Sphere、Rosenbrock等）。
  • 参数配置 ：
    • 维度（dimension）
    • 种群大小（population_size）
    • 最大迭代次数（max_iter）
    • 搜索边界（仅对部分函数开放）
  • 执行按钮 ：触发run_optimization函数运行算法。
  • 状态显示：展示最新运行结果（如收敛迭代次数、最优适应值、执行时间等）。
(3) 主界面布局
  • 左侧列（优化结果） ：
    • 显示性能统计（最终适应值、收敛迭代次数、执行时间）。
    • 展示最优解的示例（前三个维度的值）。
  • 右侧列（收敛曲线） ：
    • 使用matplotlib绘制对数坐标收敛曲线，展示最佳适应度随迭代的变化。
    • 提供下载收敛曲线的功能。

3. 核心功能：run_optimization函数

复制代码 
def run_optimization():
    # 创建MSIDBO实例
    optimizer = MSIDBO(
        objective_func=TEST_FUNCTIONS[function_name],
        dim=dim,
        lb=lb,
        ub=ub,
        population_size=population_size,
        max_iter=max_iter,
        verbose=False
    )
    
    # 运行算法
    start_time = time.time()
    best_solution, best_fitness, history = optimizer.run()
    exec_time = time.time() - start_time
    
    # 保存结果到session_state
    stats = {
        "function": function_name,
        "dimension": dim,
        "convergence_iter": optimizer.convergence_iter,
        "execution_time": exec_time,
        "final_fitness": best_fitness,
        "population_size": population_size
    }
    st.session_state.stats = stats
    st.session_state.history = history
    st.session_state.solution = best_solution
    
    # 绘制收敛曲线
    fig, ax = plt.subplots(figsize=(10, 5))
    ax.semilogy(history)
    ax.set_title(...)
    ax.grid(True)
    
    # 标记收敛点（若有）
    if optimizer.convergence_iter > 0:
        ax.axvline(...)
        ax.text(...)
    
    st.session_state.convergence_plot = fig
  • 功能 ：
    • 实例化MSIDBO优化器。
    • 运行算法并记录执行时间。
    • 保存结果到st.session_state供界面展示。
    • 生成收敛曲线并保存到st.session_state。

4. 收敛曲线绘制

  • 对数坐标图 ：使用ax.semilogy(history)绘制适应度变化，更清晰地展示收敛过程。
  • 收敛点标记：若算法在迭代中达到预设精度，用垂直线标记收敛点。

5. 界面交互与结果展示

  • 左侧列 ：
    • 显示性能统计（如final_fitness、execution_time）。
    • 展示最优解的示例值（前三个维度）。
  • 右侧列 ：

    • 动态生成收敛曲线。

    • 提供下载功能（通过st.download_button）。

      import numpy as np
      import streamlit as st
      import matplotlib.pyplot as plt
      from scipy.stats import t
      import time
      import base64
      import io
      import math
      import matplotlib.font_manager as fm

      设置中文字体支持

      try:
      # 尝试使用系统自带的中文字体
      plt.rcParams['font.sans-serif'] = ['SimHei', 'Microsoft YaHei', 'KaiTi', 'FangSong', 'STSong', 'STKaiti']
      plt.rcParams['axes.unicode_minus'] = False
      except:
      # 如果系统没有中文字体，尝试使用matplotlib的默认字体
      plt.rcParams['font.sans-serif'] = ['DejaVu Sans']
      plt.rcParams['axes.unicode_minus'] = False

      class MSIDBO:
      """改进的蜣螂优化算法实现"""
      def init(self, objective_func, dim=30, lb=-100, ub=100, population_size=50,
      max_iter=500, K=0.5, u=1.0, v=1.0, S=1.0, w=0.5, verbose=True):
      """
      初始化算法参数

      复制代码 
          Parameters:
    objective_func (function): 目标函数
    dim (int): 问题维度
    lb (float or list): 下界
    ub (float or list): 上界
    population_size (int): 种群大小
    max_iter (int): 最大迭代次数
    K (float): 反向学习参数 (0,1)
    u (float): 螺旋形状常数
    v (float): 螺旋形状常数
    S (float): 偷窃蜣螂常数
    w (float): t分布变异的缩放因子
    verbose (bool): 是否打印迭代信息
    """
    self.obj_func = objective_func
    self.dim = dim
    self.lb = np.array(lb) if isinstance(lb, list) else np.full(dim, lb)
    self.ub = np.array(ub) if isinstance(ub, list) else np.full(dim, ub)
    self.pop_size = population_size
    self.max_iter = max_iter
    self.K = K
    self.u = u
    self.v = v
    self.S = S
    self.w = w
    self.verbose = verbose
    
    # 子种群比例
    self.roller_ratio = 0.4   # 滚球蜣螂
    self.breeder_ratio = 0.3  # 繁殖蜣螂
    self.minor_ratio = 0.2    # 小蜣螂
    self.thief_ratio = 0.1    # 偷窃蜣螂
    
    # 收敛迭代次数
    self.convergence_iter = -1
    
    # 计算结果存储
    self.g_best_pos = None
    self.g_best_fit = float('inf')
    self.fitness_history = []

def spm_chaos_mapping(self):
    """SPM混沌映射生成混沌序列 (向量化优化版本)"""
    # 参数设置
    eta = 0.4
    mu = 0.3
    pop = np.random.uniform(0, 1, (self.pop_size * 2, self.dim))
    
    # 迭代生成混沌序列 (减少到5次迭代)
    for _ in range(5):
        # 划分不同区域
        mask0 = (0 <= np.abs(pop)) & (np.abs(pop) < eta)
        mask1 = (eta <= np.abs(pop)) & (np.abs(pop) < 0.5)
        mask2 = (0.5 <= np.abs(pop)) & (np.abs(pop) < 1 - eta)
        mask3 = (1 - eta <= np.abs(pop)) & (np.abs(pop) < 1)
        
        # 分别处理不同区域的点
        pop[mask0] = np.mod(pop[mask0] / eta + mu * np.sin(np.pi * pop[mask0]) + 
                           np.random.random(pop[mask0].shape) * 0.01, 1)
        
        pop[mask1] = np.mod(pop[mask1] / (0.5 - eta) + mu * np.sin(np.pi * pop[mask1]) + 
                           np.random.random(pop[mask1].shape) * 0.01, 1)
        
        pop[mask2] = np.mod((1 - pop[mask2]) / (0.5 - eta) + mu * np.sin(np.pi * (1 - pop[mask2])) + 
                           np.random.random(pop[mask2].shape) * 0.01, 1)
        
        pop[mask3] = np.mod((1 - pop[mask3]) / eta + mu * np.sin(np.pi * (1 - pop[mask3])) + 
                           np.random.random(pop[mask3].shape) * 0.01, 1)
    
    return pop

def map_to_solution_space(self, chaos_pop):
    """将[0,1]映射到解空间"""
    return self.lb + (self.ub - self.lb) * chaos_pop

def opposition_learning(self, population):
    """反向学习生成反向解"""
    center = self.K * (self.lb + self.ub)
    return np.clip(center - population, self.lb, self.ub)

def spm_chaos_opposition_init(self):
    """SPM混沌反向学习初始化"""
    # SPM混沌映射生成种群
    spm_pop = self.spm_chaos_mapping()
    spm_pop = self.map_to_solution_space(spm_pop)
    
    # 反向学习生成种群
    opposite_pop = self.opposition_learning(spm_pop)
    
    # 合并种群并选择最优个体
    combined_pop = np.vstack([spm_pop, opposite_pop])
    fitness = np.array([self.obj_func(ind) for ind in combined_pop])
    sorted_indices = np.argsort(fitness)
    return combined_pop[sorted_indices[:self.pop_size]]

def improved_R_factor(self, t):
    """改进的边界收敛因子"""
    x = 2 * t / self.max_iter - 1
    return ((x**3 - 3*x + 2) / 4)

def update_global_best(self, fitness):
    """更新全局最优解"""
    min_idx = np.argmin(fitness)
    if fitness[min_idx] < self.g_best_fit:
        self.g_best_fit = fitness[min_idx]
        self.g_best_pos = self.population[min_idx].copy()
        
        # 首次达到接近0的精度时记录收敛
        if self.g_best_fit < 1e-12 and self.convergence_iter == -1:
            self.convergence_iter = self.current_iter + 1

def roll_ball(self, i, Xw):
    """滚球蜣螂更新"""
    # 90%概率滚球，10%概率跳舞
    if np.random.rand() < 0.9:
        # 滚球行为
        delta_x = self.population[i] - Xw
        alpha = np.random.choice([1, -1], size=self.dim)
        k = np.random.uniform(0, 0.2, size=self.dim)
        b = np.random.uniform(0, 1, size=self.dim)
        return self.population[i] + alpha * k * delta_x + b * delta_x
    else:
        # 跳舞行为
        displacement = self.population[i] - self.prev_positions[i]
        theta = np.random.uniform(0, np.pi)
        # 避免theta接近π/2导致数值不稳定
        if np.abs(theta - np.pi/2) < 0.01:
            theta = np.pi/2 + 0.1
        return self.population[i] + np.tan(theta) * displacement

def breeder(self, i, R):
    """繁殖蜣螂更新（融合海鸥螺旋攻击）"""
    # 计算边界
    L_star_b = np.maximum(self.g_best_pos * (1 - R), self.lb)
    U_star_b = np.minimum(self.g_best_pos * (1 + R), self.ub)
    
    # 海鸥螺旋攻击机制
    beta = np.random.uniform(0, 2 * np.pi)
    r = self.u * np.exp(beta * self.v)
    x_prime = r * np.cos(beta)
    y_prime = r * np.sin(beta)
    z_prime = r * beta
    spiral_factor = x_prime * y_prime * z_prime
    
    # 位置更新
    b1 = np.random.uniform(0, 1, size=self.dim)
    b2 = np.random.uniform(0, 1, size=self.dim)
    return self.g_best_pos + spiral_factor * (b1 * (self.population[i] - L_star_b) + 
                                              b2 * (self.population[i] - U_star_b))

def minor(self, i, R):
    """小蜣螂更新"""
    # 计算边界
    L_bb = np.maximum(self.g_best_pos * (1 - R), self.lb)
    U_bb = np.minimum(self.g_best_pos * (1 + R), self.ub)
    
    # 位置更新
    C1 = np.random.randn()
    C2 = np.random.uniform(0, 1, size=self.dim)
    return self.population[i] + C1 * (self.population[i] - L_bb) + C2 * (self.population[i] - U_bb)

def thief(self, i):
    """偷窃蜣螂更新"""
    g = np.random.randn(self.dim)
    dist = np.abs(self.population[i] - self.g_best_pos)
    return self.g_best_pos + self.S * g * dist

def t_distribution_mutation(self):
    """t-分布差分变异"""
    new_pop = np.copy(self.population)
    new_fitness = np.copy(self.fitness)
    
    for i in range(self.pop_size):
        # 随机选择另一个体
        r = np.random.randint(self.pop_size)
        
        # 确保自由度有效
        df = max(1, self.current_iter)
        
        # t分布的随机数 (自由度为当前迭代次数)
        gamma1 = t.rvs(df=df, size=self.dim)
        gamma2 = t.rvs(df=df, size=self.dim)
        
        # 差分变异
        new_pos = self.population[i] + self.w * (gamma1 * (self.g_best_pos - self.population[i]) + 
                                                gamma2 * (self.population[r] - self.population[i]))
        
        # 边界检查
        new_pos = np.clip(new_pos, self.lb, self.ub)
        
        # 贪婪选择
        new_fit = self.obj_func(new_pos)
        if new_fit < self.fitness[i]:
            new_pop[i] = new_pos
            new_fitness[i] = new_fit
    
    return new_pop, new_fitness

def run(self):
    """执行算法主循环"""
    # 初始化种群
    self.population = self.spm_chaos_opposition_init()
    self.prev_positions = np.copy(self.population)
    self.fitness = np.array([self.obj_func(ind) for ind in self.population])
    self.update_global_best(self.fitness)
    self.fitness_history.append(self.g_best_fit)
    self.convergence_iter = -1
    
    if self.verbose:
        print(f"Iter 1/{self.max_iter}, Best Fitness: {self.g_best_fit:.6f}")
    
    for t in range(self.max_iter):
        self.current_iter = t
        
        # 保存上一代位置（用于跳舞行为）
        self.prev_positions = np.copy(self.population)
        
        # 计算改进的R因子
        R = self.improved_R_factor(t)
        
        # 划分子种群
        roller_end = int(self.pop_size * self.roller_ratio)
        breeder_end = int(self.pop_size * (self.roller_ratio + self.breeder_ratio))
        minor_end = int(self.pop_size * (self.roller_ratio + self.breeder_ratio + self.minor_ratio))
        
        # 更新全局最差解位置
        worst_idx = np.argmax(self.fitness)
        Xw = self.population[worst_idx]
        
        # 更新滚球蜣螂
        for i in range(roller_end):
            new_pos = self.roll_ball(i, Xw)
            self.population[i] = np.clip(new_pos, self.lb, self.ub)
        
        # 更新繁殖蜣螂
        for i in range(roller_end, breeder_end):
            new_pos = self.breeder(i, R)
            self.population[i] = np.clip(new_pos, self.lb, self.ub)
        
        # 更新小蜣螂
        for i in range(breeder_end, minor_end):
            new_pos = self.minor(i, R)
            self.population[i] = np.clip(new_pos, self.lb, self.ub)
        
        # 更新偷窃蜣螂
        for i in range(minor_end, self.pop_size):
            new_pos = self.thief(i)
            self.population[i] = np.clip(new_pos, self.lb, self.ub)
        
        # 计算新适应度
        self.fitness = np.array([self.obj_func(ind) for ind in self.population])
        
        # 更新全局最优解
        self.update_global_best(self.fitness)
        
        # t-分布差分变异
        self.population, self.fitness = self.t_distribution_mutation()
        
        # 更新全局最优解（变异后）
        self.update_global_best(self.fitness)
        
        # 记录历史最优适应度
        self.fitness_history.append(self.g_best_fit)
        
        # 打印迭代信息
        if self.verbose and (t % 50 == 0 or t == self.max_iter - 1):
            print(f"Iter {t+1}/{self.max_iter}, Best Fitness: {self.g_best_fit:.6f}")
    
    return self.g_best_pos, self.g_best_fit, self.fitness_history

      测试函数集合

      TEST_FUNCTIONS = {
      "Sphere": lambda x: np.sum(x2),
      "Rastrigin": lambda x: 10 * len(x) + np.sum(x      2 - 10 * np.cos(2 * np.pi * x)),
      "Ackley": lambda x: 20 - 20 * np.exp(-0.2 * np.sqrt(np.mean(x**2))) + math.e - np.exp(np.mean(np.cos(2 * np.pi * x))),
      "Rosenbrock": lambda x: np.sum(100 * (x[1:] - x[:-1]**2)**2 + (1 - x[:-1])**2),
      "Schwefel": lambda x: 418.9829 * len(x) - np.sum(x * np.sin(np.sqrt(np.abs(x))))
      }

      def run_optimization():
      """执行优化算法并显示结果"""
      st.sidebar.subheader("优化进度")
      progress_bar = st.sidebar.progress(0)
      status_text = st.sidebar.empty()

      复制代码 
      # 获取参数
function_name = st.session_state.selected_function
dim = st.session_state.dimension
pop_size = st.session_state.population_size
max_iter = st.session_state.max_iter
lb = st.session_state.lower_bound
ub = st.session_state.upper_bound
save_plot = st.session_state.save_plot

# 设置问题边界
if function_name == "Schwefel":
    lb = -500
    ub = 500
elif function_name == "Rosenbrock":
    lb = -30
    ub = 30

# 创建优化器
optimizer = MSIDBO(
    objective_func=TEST_FUNCTIONS[function_name],
    dim=dim,
    lb=lb,
    ub=ub,
    population_size=pop_size,
    max_iter=max_iter,
    verbose=False
)

# 运行优化算法
start_time = time.time()
best_solution, best_fitness, history = optimizer.run()
exec_time = time.time() - start_time

# 更新性能统计
stats = {
    "function": function_name,
    "dimension": dim,
    "convergence_iter": optimizer.convergence_iter,
    "execution_time": exec_time,
    "final_fitness": best_fitness,
    "population_size": pop_size
}

# 保存结果
st.session_state.stats = stats
st.session_state.history = history
st.session_state.solution = best_solution

# 绘制收敛曲线
fig, ax = plt.subplots(figsize=(10, 5))
ax.semilogy(history)
ax.set_title(f'MSIDBO收敛曲线\n({function_name}, 维度={dim})')
ax.set_xlabel('迭代次数')
ax.set_ylabel('最佳适应度 (对数刻度)')
ax.grid(True)

if optimizer.convergence_iter > 0:
    ax.axvline(x=optimizer.convergence_iter, color='r', linestyle='--', alpha=0.7)
    ax.text(optimizer.convergence_iter + max_iter*0.02, plt.ylim()[1] * 0.9, 
           f'收敛于迭代 {optimizer.convergence_iter}', color='r')

st.session_state.convergence_plot = fig
status_text.success("优化完成!")
progress_bar.progress(100)

      def main():
      st.set_page_config(
      page_title="蜣螂优化算法平台",
      page_icon="🐞",
      layout="wide"
      )

      复制代码 
      # 页面标题
st.title("🐞 改进蜣螂优化算法(MSIDBO)交互平台")
st.markdown("""
    **蜣螂优化算法(DBO)** 是一种受自然界蜣螂行为启发的新型智能优化算法。本平台实现了改进版算法(MSIDBO)，
    包含空间金字塔混沌初始化、改进边界收敛因子等优化策略。
""")

# 初始化session状态
if 'stats' not in st.session_state:
    st.session_state.stats = None
if 'history' not in st.session_state:
    st.session_state.history = None
if 'solution' not in st.session_state:
    st.session_state.solution = None
if 'convergence_plot' not in st.session_state:
    st.session_state.convergence_plot = None
if 'selected_function' not in st.session_state:
    st.session_state.selected_function = "Sphere"
if 'dimension' not in st.session_state:
    st.session_state.dimension = 30
if 'population_size' not in st.session_state:
    st.session_state.population_size = 50
if 'max_iter' not in st.session_state:
    st.session_state.max_iter = 500
if 'lower_bound' not in st.session_state:
    st.session_state.lower_bound = -100
if 'upper_bound' not in st.session_state:
    st.session_state.upper_bound = 100
if 'save_plot' not in st.session_state:
    st.session_state.save_plot = False

# 侧边栏配置
with st.sidebar:
    st.header("算法配置")
    
    # 问题选择
    st.session_state.selected_function = st.selectbox(
        "选择优化问题:",
        list(TEST_FUNCTIONS.keys()),
        key="func_select"
    )
    
    # 参数配置
    st.session_state.dimension = st.slider(
        "问题维度:", min_value=10, max_value=100, value=30, step=10
    )
    
    st.session_state.population_size = st.slider(
        "种群大小:", min_value=10, max_value=200, value=50, step=10
    )
    
    st.session_state.max_iter = st.slider(
        "最大迭代次数:", min_value=100, max_value=2000, value=500, step=100
    )
    
    # 仅当函数不是固定边界时才显示边界设置
    if st.session_state.selected_function not in ["Schwefel", "Rosenbrock"]:
        col1, col2 = st.columns(2)
        with col1:
            st.session_state.lower_bound = st.number_input(
                "搜索下界:", value=-100.0, key="lb_input"
            )
        with col2:
            st.session_state.upper_bound = st.number_input(
                "搜索上界:", value=100.0, key="ub_input"
            )
    
    st.session_state.save_plot = st.checkbox(
        "自动保存收敛曲线", value=True
    )
    
    # 执行按钮
    st.markdown("---")
    if st.button("执行优化算法", key="run_btn", use_container_width=True):
        run_optimization()
    
    # 状态显示
    if st.session_state.stats:
        st.markdown("### 最新结果")
        st.write(f"函数: {st.session_state.stats['function']}")
        st.write(f"维度: {st.session_state.stats['dimension']}")
        st.write(f"收敛迭代: {st.session_state.stats.get('convergence_iter', 'N/A')}/{st.session_state.max_iter}")
        st.write(f"最优适应值: {st.session_state.stats['final_fitness']:.6e}")
        st.write(f"执行时间: {st.session_state.stats['execution_time']:.2f}秒")

# 主显示区域
col1, col2 = st.columns([1, 1])

with col1:
    st.header("优化结果")
    
    if st.session_state.stats:
        stats = st.session_state.stats
        
        st.subheader("性能统计")
        st.metric("最终适应值", f"{stats['final_fitness']:.6e}")
        
        convergence_info = "未收敛"
        if stats.get('convergence_iter', -1) > 0:
            convergence_info = f"{stats['convergence_iter']}/{st.session_state.max_iter}"
        st.metric("收敛于迭代", convergence_info)
        
        st.metric("执行时间", f"{stats['execution_time']:.2f}秒")
        
        st.subheader("最优解示例")
        st.code(f"维度0: {st.session_state.solution[0]:.4f}\n" +
                f"维度1: {st.session_state.solution[1]:.4f}\n" +
                f"维度2: {st.session_state.solution[2]:.4f}\n" +
                (f"...等{stats['dimension']}个维度" if stats['dimension'] > 3 else ""))
    
    else:
        st.info("请配置算法参数并点击'执行优化算法'运行")

with col2:
    st.header("收敛曲线")
    
    if st.session_state.convergence_plot:
        st.pyplot(st.session_state.convergence_plot)
        
        if st.session_state.save_plot:
            buf = io.BytesIO()
            st.session_state.convergence_plot.savefig(buf, format="png", dpi=150)
            buf.seek(0)
            st.download_button(
                label="下载收敛曲线",
                data=buf,
                file_name=f"convergence_{st.session_state.selected_function}_d{st.session_state.dimension}.png",
                mime="image/png"
            )
    else:
        st.image("https://via.placeholder.com/600x400.png?text=等待算法运行...", width=500)

# 算法描述
st.markdown("---")
st.header("算法原理概述")
with st.expander("查看蜣螂优化算法细节"):
    st.markdown("""
    ### 蜣螂优化算法(DBO)
    
    蜣螂优化算法根据蜣螂的不同行为划分为4个子种群：
    
    1. **滚球蜣螂**：模拟蜣螂滚粪球的直线移动和遇障碍物跳舞重新定位的行为
    2. **繁殖蜣螂**：模拟将粪球埋入地下，在安全区域繁殖后代的行为
    3. **小蜣螂**：模拟幼虫长大后的觅食行为
    4. **偷窃蜣螂**：模拟偷窃其他蜣螂粪球的行为
    
    ### 改进算法(MSIDBO)
    
    本实现包含以下优化策略：
    
    - **空间金字塔匹配混沌反向学习初始化**：提高种群多样性和初始解质量
    - **改进边界收敛因子**：非线性动态调整搜索范围，平衡全局和局部搜索
    - **融合海鸥优化算法**：加入螺旋攻击机制增强局部开发能力
    - **t-分布差分变异**：增加算法跳出局部最优能力
    
    这些改进策略显著提高了算法的收敛速度和全局优化能力。
    """)

      if name == "main":
      main()

相关推荐
LiuYiCheng12345642 分钟前
Python游戏开发：Pygame全面指南与实战
python·pygame
魔障阿Q1 小时前
华为310P3模型转换及python推理
人工智能·python·深度学习·yolo·计算机视觉·华为
都叫我大帅哥2 小时前
决策树：从零开始的机器学习“算命大师”修炼手册
python·机器学习
这里有鱼汤2 小时前
首个支持A股的AI多智能体金融系统，来了
前端·python
云霄IT2 小时前
python使用ffmpeg录制rtmp/m3u8推流视频并按ctrl+c实现优雅退出
python·ffmpeg·音视频
都叫我大帅哥2 小时前
我给大模型装上“记忆黄金券”：LangChain的ConversationSummaryBufferMemory全解析
python·langchain·ai编程
桃子叔叔2 小时前
28天0基础前端工程师完成Flask接口编写
前端·python·flask
德育处主任3 小时前
『OpenCV-Python』配合 Matplotlib 显示图像
后端·python·opencv
仰望星空的凡人9 小时前
【JS逆向基础】数据库之MongoDB
javascript·数据库·python·mongodb
热门推荐
01Qwen3-Coder 快速上手教程 | Qwen Code + Claude Code02全球最强模型Grok4，国内已可免费使用！（附教程）03Coze 开源了，送上保姆级私有化部署方案【建议收藏】04扣子开源本地部署教程 丨Coze智能体小白喂饭级指南05KGG转MP3工具|非KGM文件|解密音频06腾讯还是太全面了，限时免费！超全CodeBuddy IDE保姆级教程！（附案例）07【手把手攻略】国家育儿补贴正式开领！一键算清你能拿多少钱？附补贴领取计算器0801-开源版COZE-字节 Coze Studio 重磅开源！保姆级本地安装教程，手把手带你体验09干翻 Typora！MilkUp：完全免费的桌面端 Markdown 编辑器！10coze 开源版本地部署及踩过的坑【喂饭级教程】