P8328 [COCI 2021/2022 #5] Usmjeravanj
本题的实际难度和通过数不是相符。
实际思维难度:蓝
代码实现难度:绿
部分1、简化题意
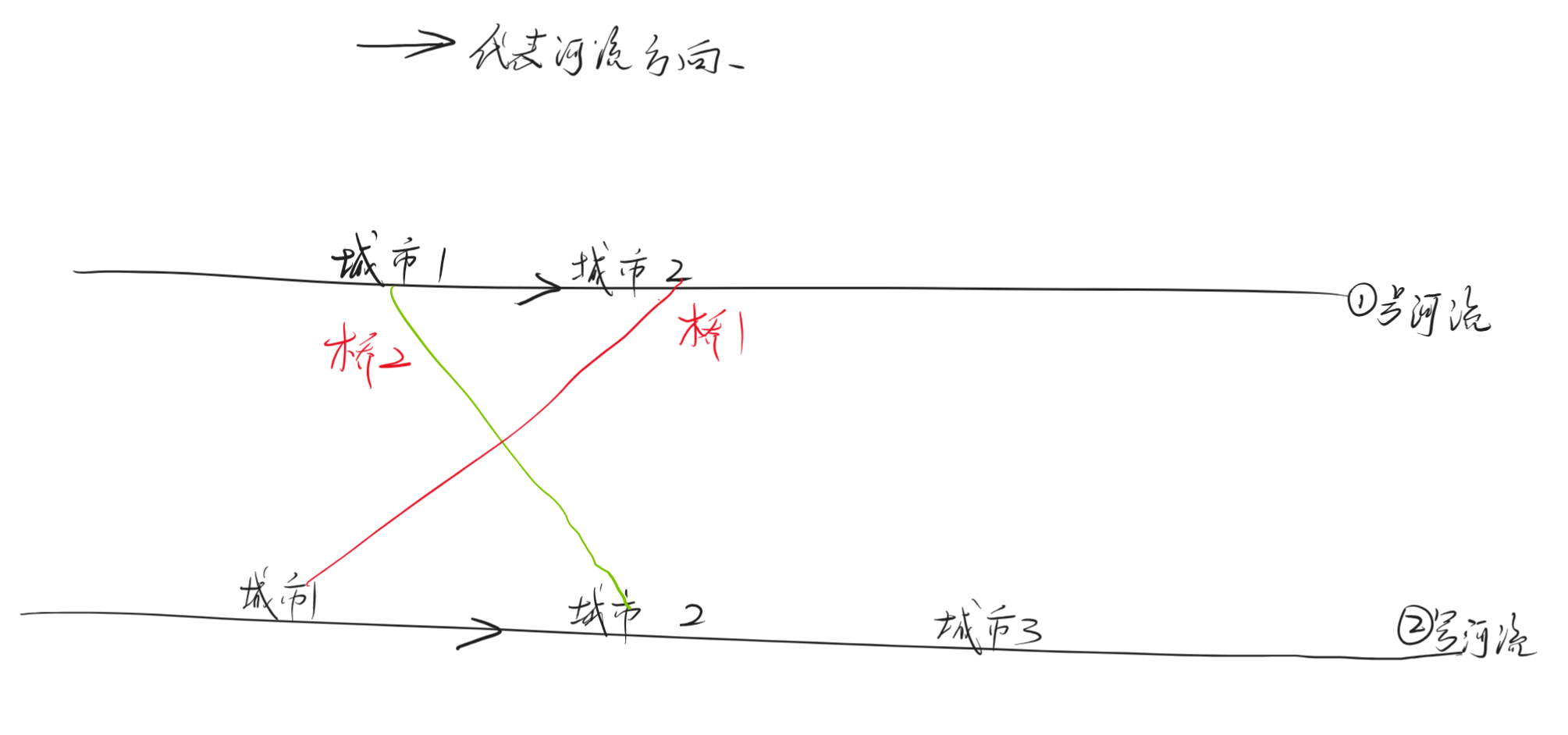
存在两条河流,假设分别叫做① 和 ②。
其中①号河流有 \(a\) 座城市, ② 号河流有 \(b\) 座城市。
河流方向是从编号小的城市流向编号大的城市,现在准备在两条河流的某些城市上建立 \(m\) 座桥, 每座桥都是单向的,请给定每座桥的方向,
其中 \(0\) 方向代表从河流 ① 上的城市到河流 ② 的城市, \(1\) 方向刚好相反。
现在需要使得强连通分量最少,请给出每座桥的具体方向(输出任意一个即可)
比如下图就是一个参考。
样例一分析:
输入:
cpp
5 3
4
1 2
2 3
3 1
5 3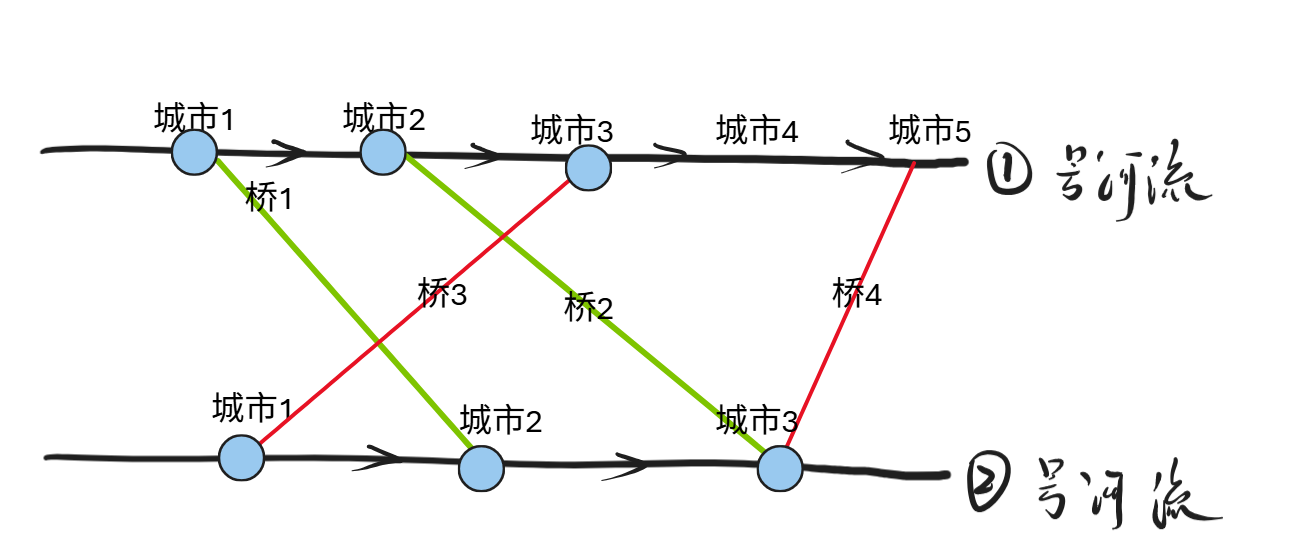
输出:
按照下方给定的最优合法方案,是按照下图所示,所有城市都是连通的。
cpp
1
1 1 0 0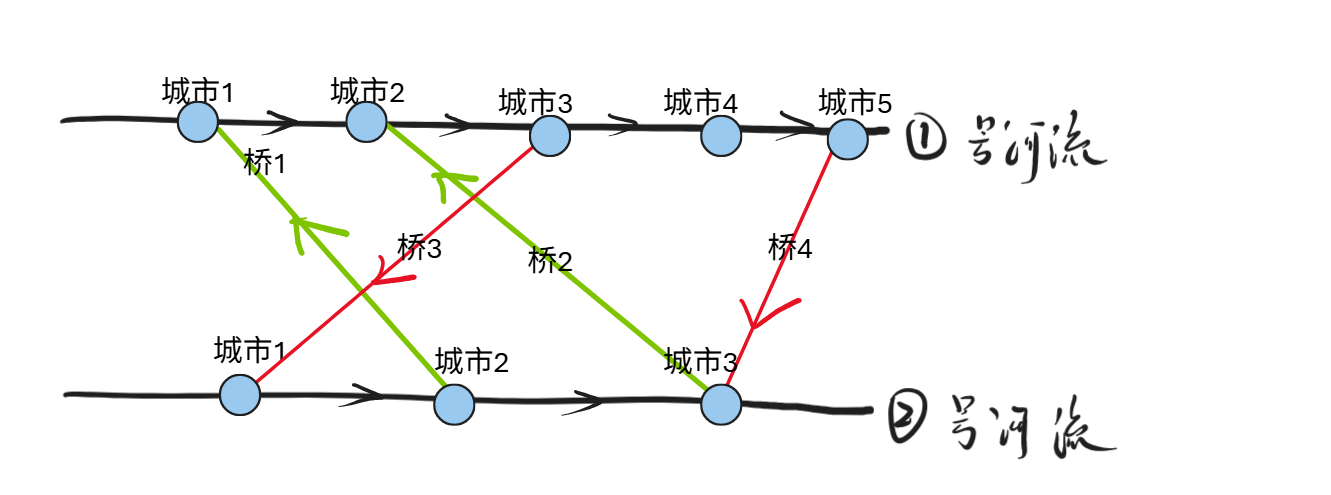
部分2、思路分析
首先上述的题目跟有向图的连通有关,大概率是强连通分量,如果没有给定边的选择,直接给定方向,直接可以建边获取得到scc。
值得注意的是,①号河流和②号河流的城市编号相同,肯定不可取,所以可以给②号河流加上一个偏移量
比如
cpp
add_edge(a[i], b[i] + n);答案求解已经得到,重点是如何建边?
首先考虑的一点是,选定合适的桥的方向,可以减少强连通分量的数量,假设目前只有两座桥,先进行分类讨论:
情况一:两座桥不交叉,并且相同方向
结论:下述四种情况,最终无论情况如何,得到的结果对scc无影响。
情况二:两座桥不交叉,并且不同方向
结论:下述四种情况,最终无论情况如何,得到的结果对scc无影响。
情况三:两座桥交叉,并且相同方向
结论:下述两种情况对scc无影响
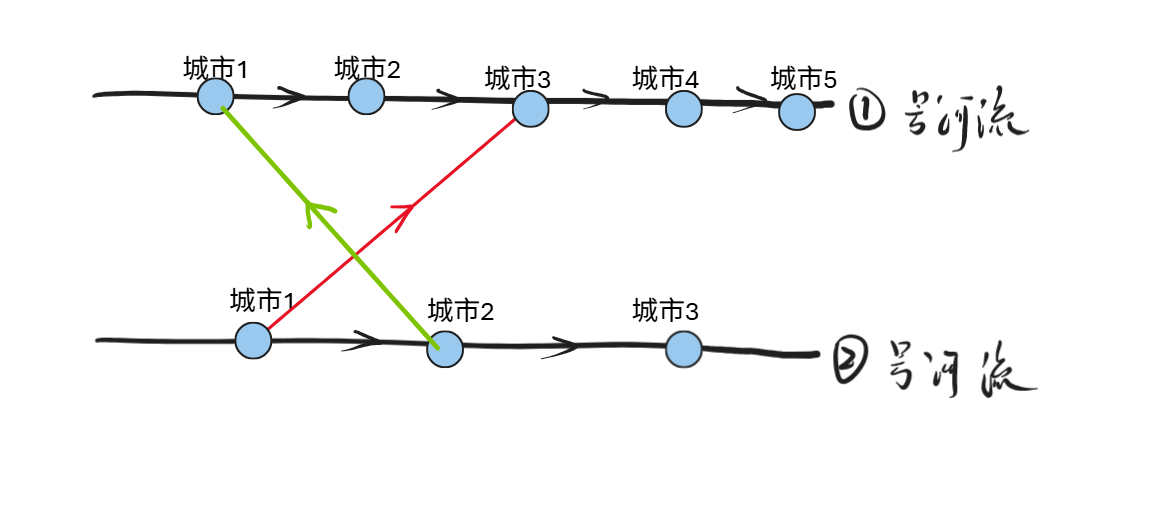
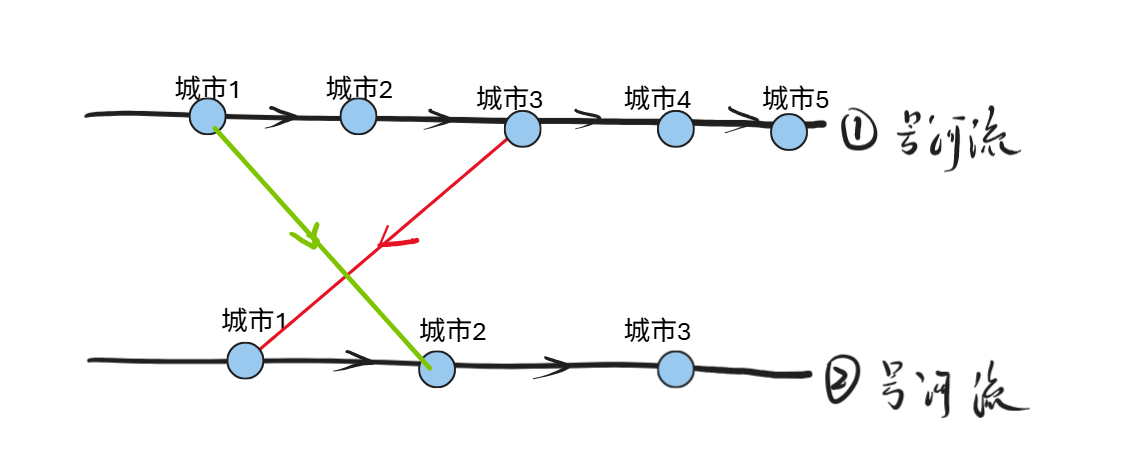
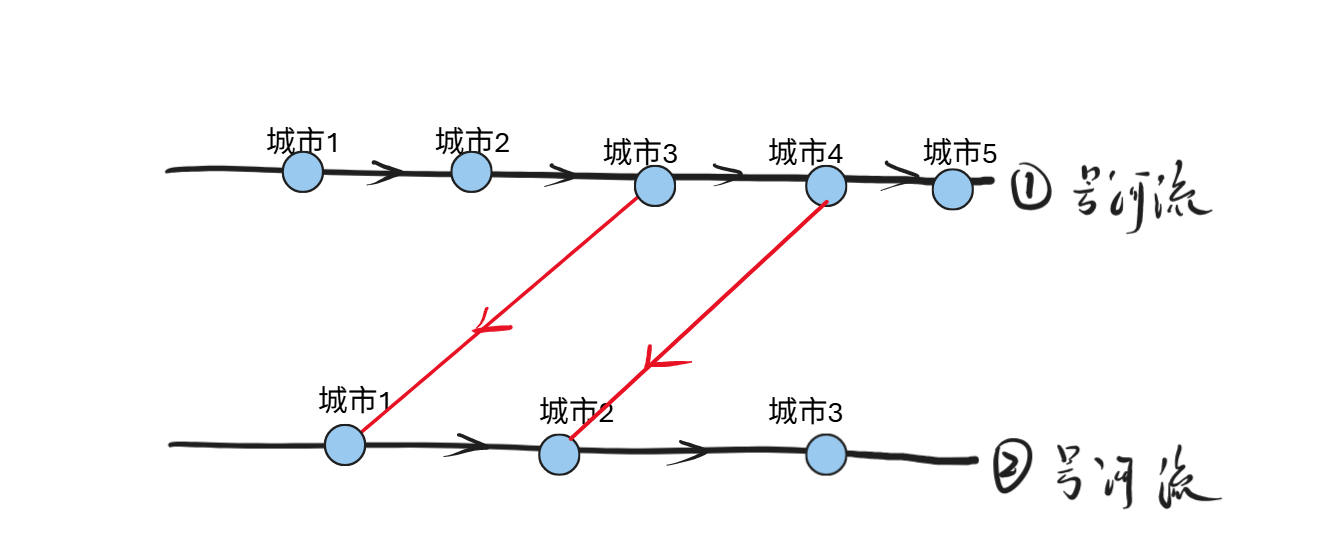
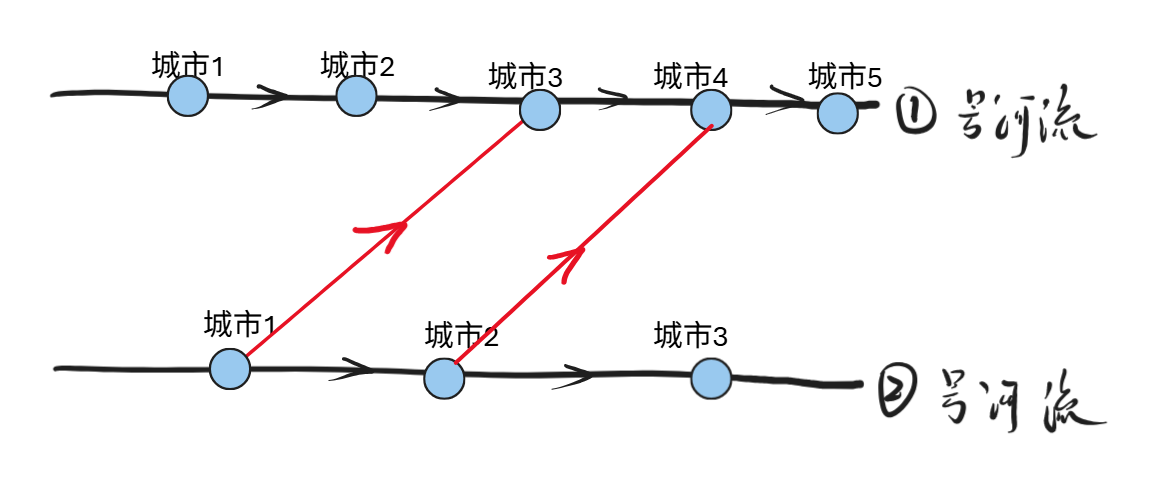
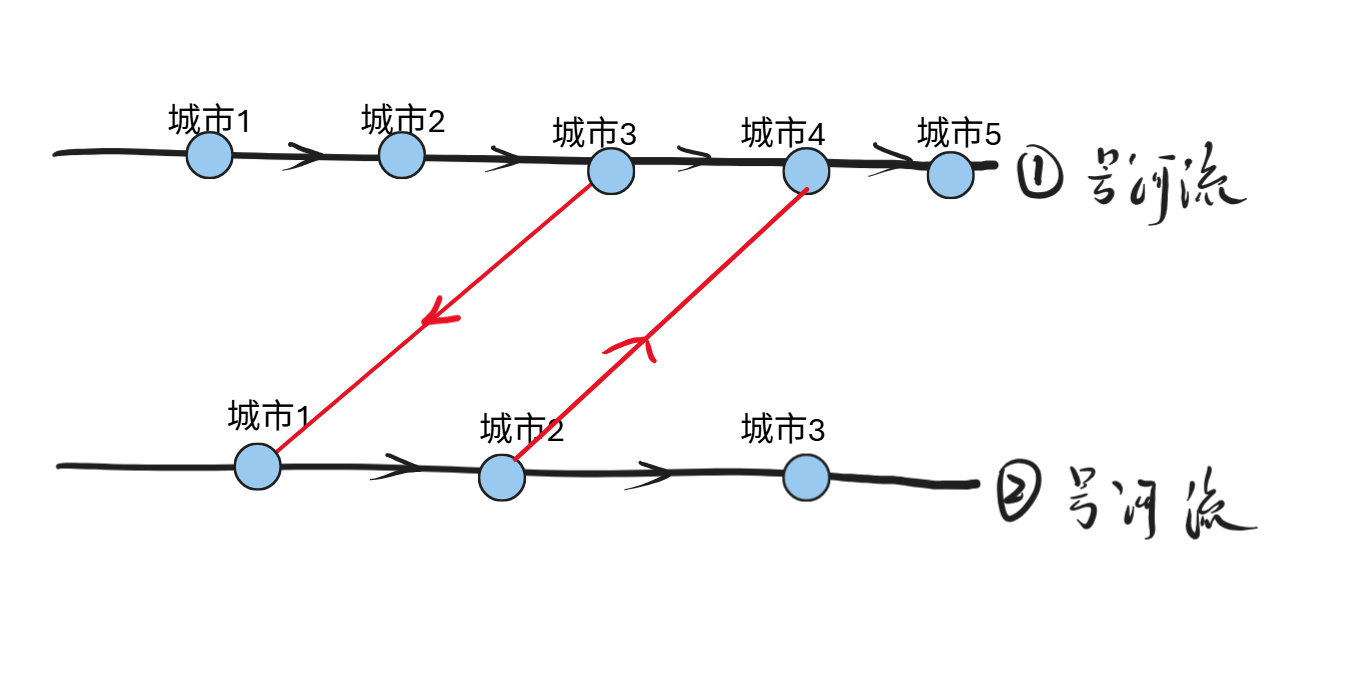
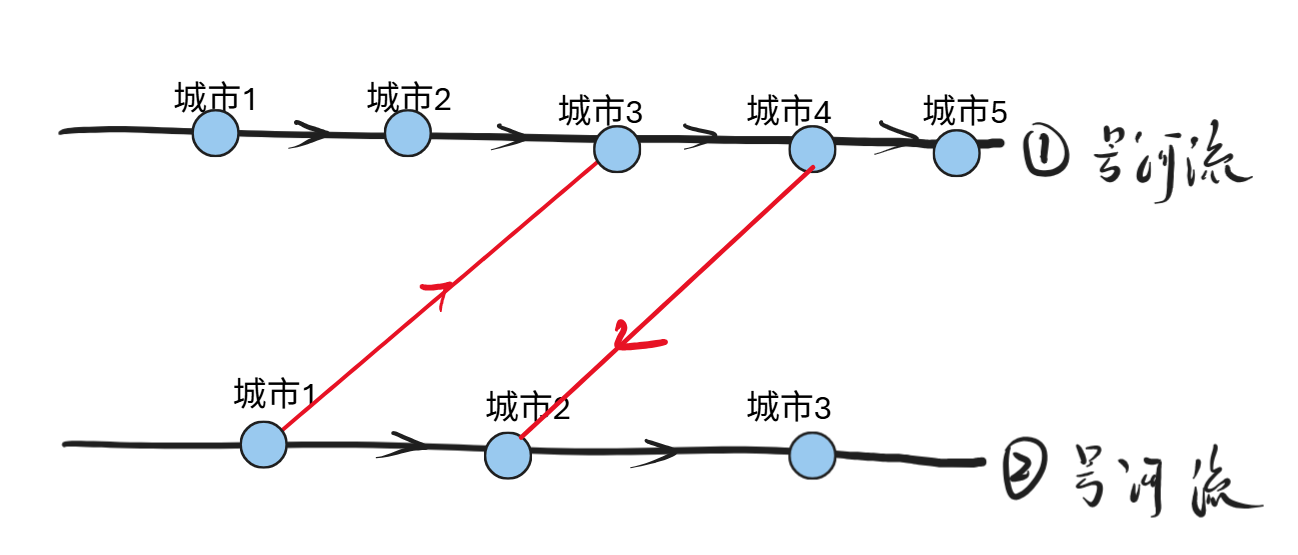
情况四:两座桥交叉,并且不同方向
结论:只有第一张图的方案可以使得scc数量减少,但是第二张图对scc无影响。
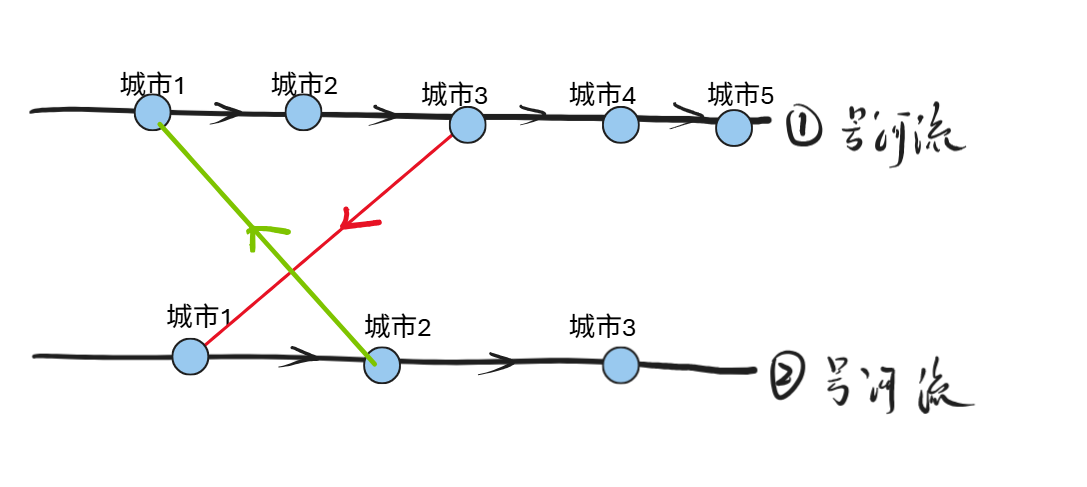
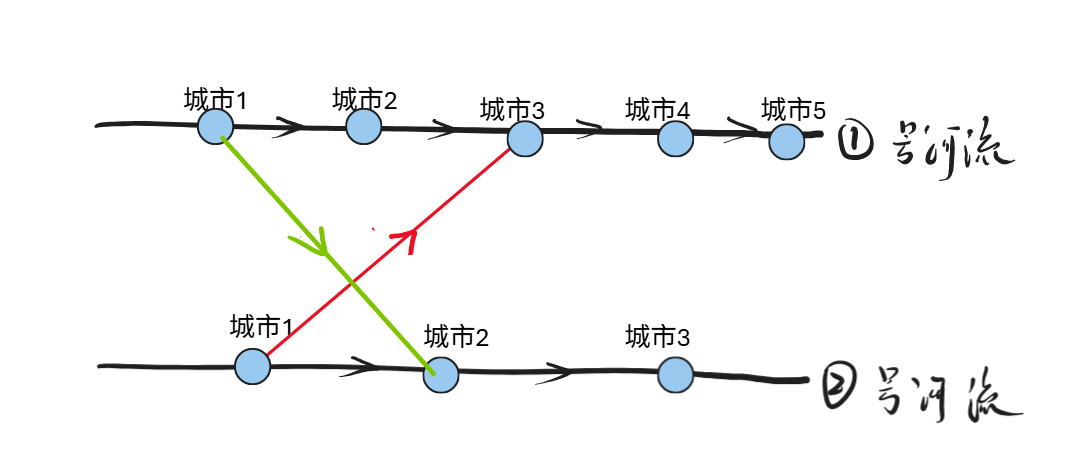
最终结论:所有的建边方向,考虑交叉之后,方向相反的答案(按照下图建边)

部分3、具体实现和代码细节
如何判断最终结论,首先假设将所有的桥进行了存储,分别标记为 \(x_i\) 和 \(y_i\) 。
桥交叉的话,只可能是以下两种选择
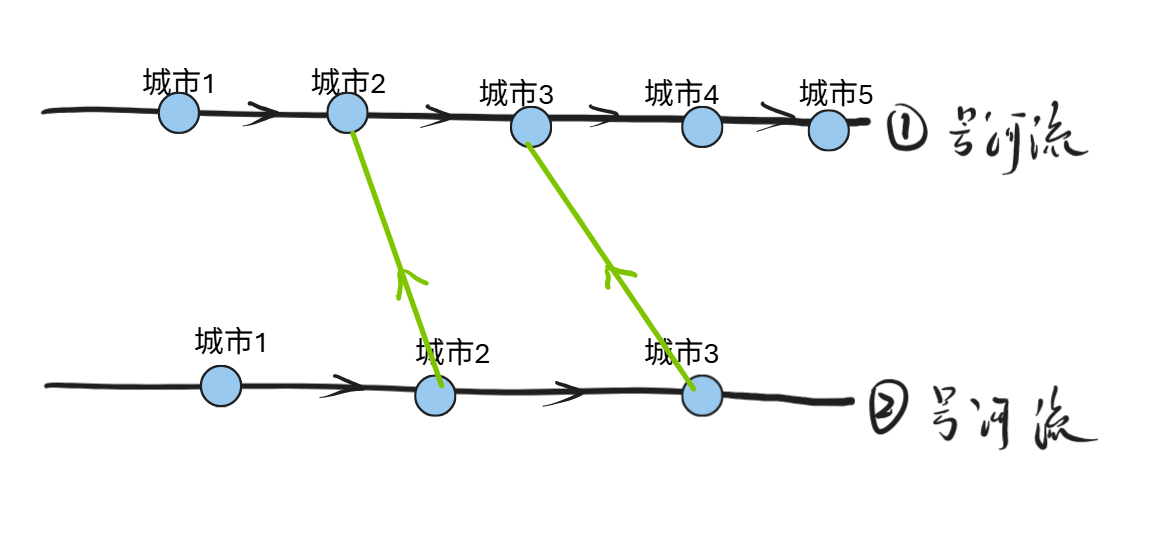
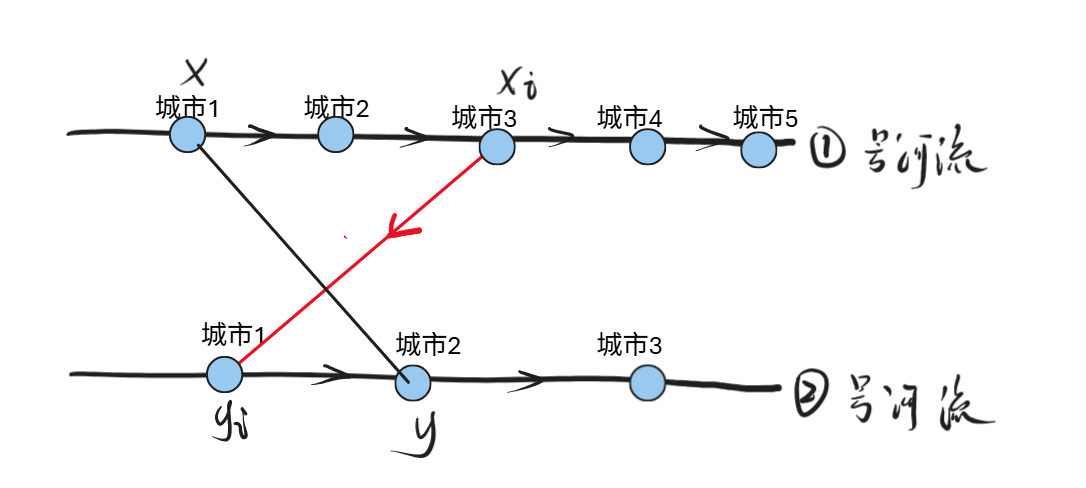
选择1、黑色桥是之前已经选择过的,红色的桥是现在需要控制方向的,此处无论黑色的桥的方向如何,
按照如下图所示的方向,从 x_i 指向 y_i 一定是最佳的。
判断方式是
x \< x _ i 并且 y_i \< y
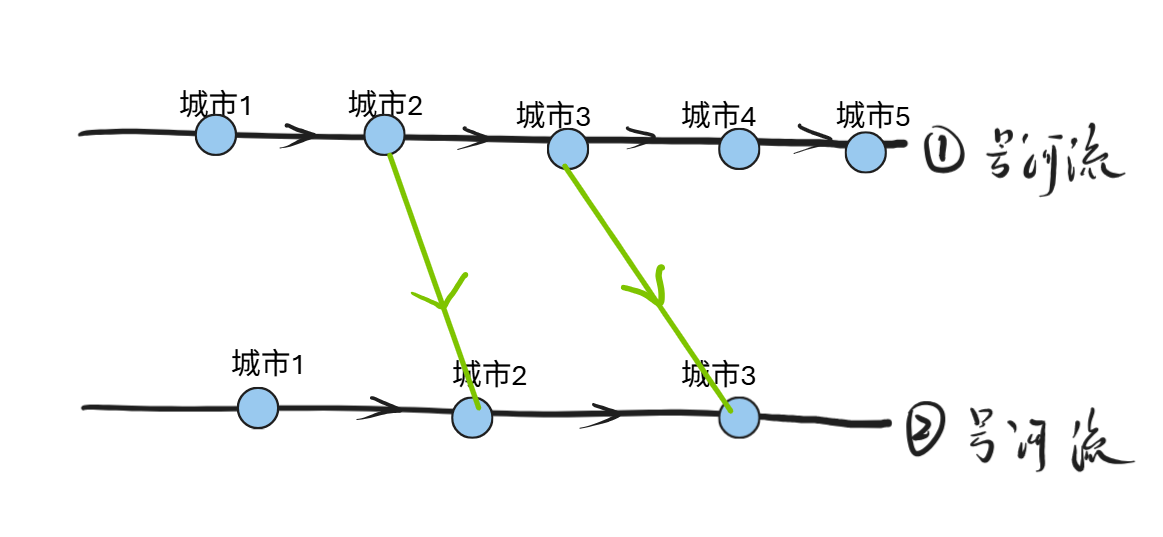
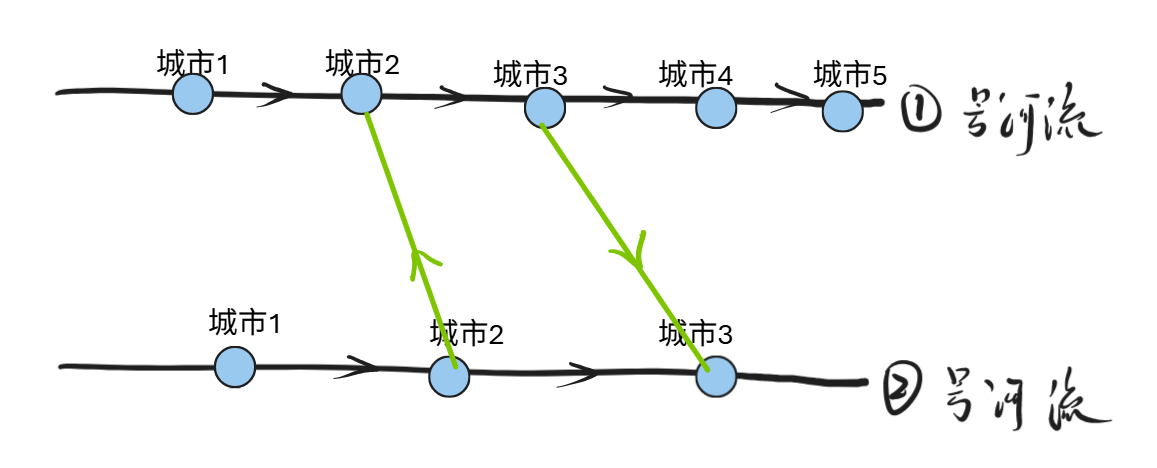
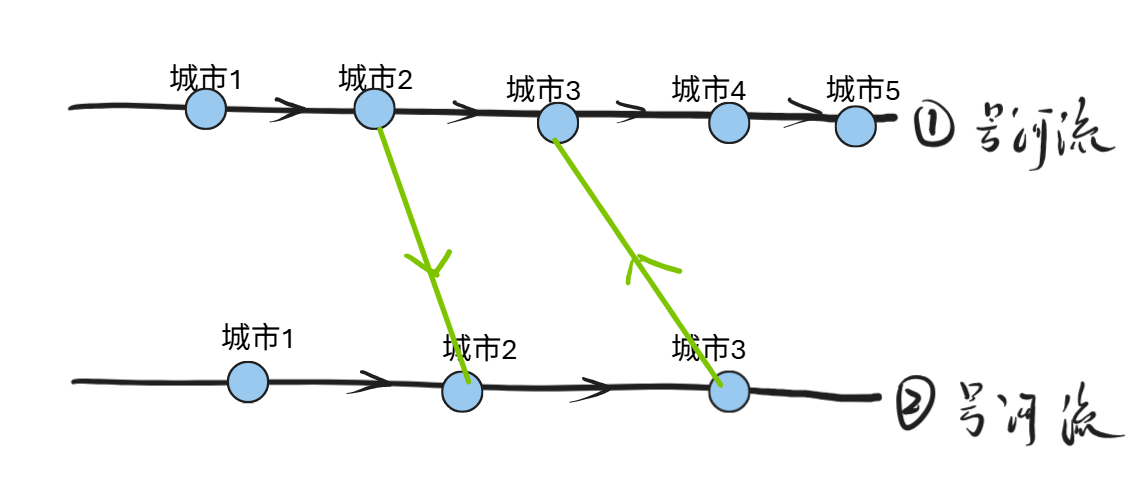
选择2、黑色桥是之后需要选择的,绿色桥是现在需要选择的方向,按照这种方式才可能交叉。
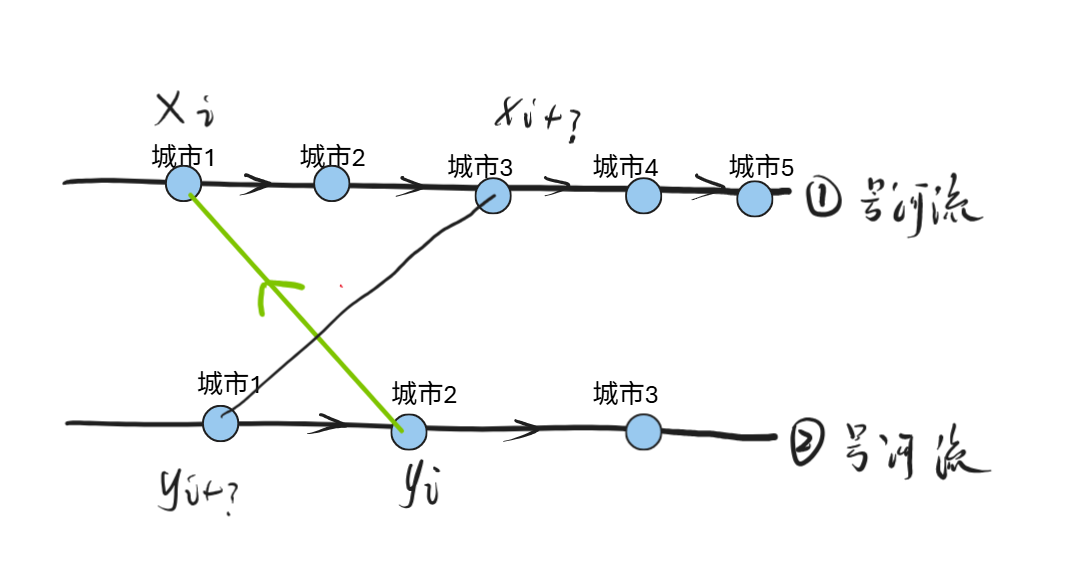
综上:桥的方向选择比较容易确定,考虑桥的选择的优先顺序,首先确立上述的绿色的边,然后确立红色的边会比较方便一些。
另外看到上述的判断方式,二维偏序关系,可以先排序处理为一维偏序。
按照 \(x\) 的顺序从小到大,这样我们在选择的时候,桥枚举的时候,①号河流的城市编号非递减,此时比较交叉的时候,下述关系的
x \< x _ i 自动满足,另外只需要找到 y_i \< y ,那么如何判断有没有交叉,需要获取 \(R = y_{max}\) ,也就是之前选择过的桥的 \(y\) 的最大值。
因为我们需要让 \(y_i\) (现在枚举的桥) 交叉的数量最多,此时的 \(y\) (之前出现过的桥) 值越大越好。
说的简单点就是,下方的两座桥,当 \(x\) 相等的时候,我们肯定会优先把后面绿色的桥的方向考虑,因为后面的桥可以交叉的数量更多。
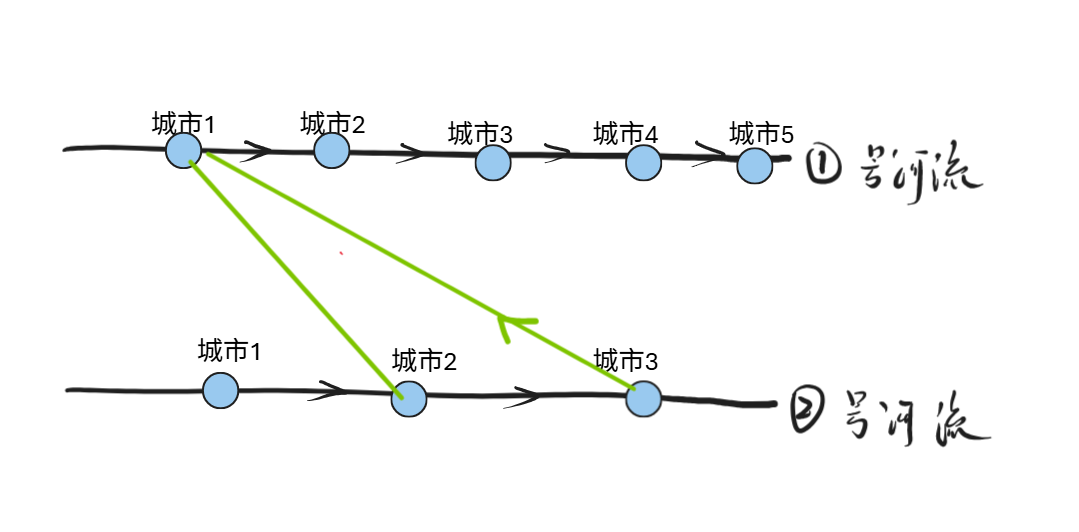
代码实现步骤:
步骤一:按照x作为第一关键词,从小到大排序,按照y作为第二关键词,从大到小排序
步骤二:如果枚举的y[i] <= R,说明有交叉,选定边的方向和上述图之中的红色边一致,也就是0方向;如果枚举的 y[i] > R ,说明没有交叉,但是此时的y更大,需要更新R, 此时按照绿色边(选择2)去处理更优,也就是 1 方向。
代码参照: