细胞如同动态演化的生态系统一样相互作用。尽管近年来的单细胞和空间多组学技术能够量化单个细胞的特征,但预测细胞的演化仍需要数学建模。这里提出了一个概念框架------细胞行为假设语法(cell behavior hypothesis grammar),该框架利用自然语言陈述(细胞规则)来创建数学模型。这使得生物学知识和多组学数据能够系统整合,从而生成计算机模拟模型,进而开展虚拟"思维实验",以此检验和拓展我们对多细胞系统的理解,并产生新的可验证假设。
Human interpretable grammar encodes multicellular systems biology models to democratize virtual cell laboratories,Cell,2025
目录
- 一种编码细胞对细胞外信号行为反应的语法
- [PhysiCell agent-based modeling framework](#PhysiCell agent-based modeling framework)
- 假设语法
- 实验设置
一种编码细胞对细胞外信号行为反应的语法
作者在经过良好校准且稳健的基于智能体的建模生态系统PhysiCell中实现了ABM假设语法[1]。像PhysiCell这样的ABM框架将单个细胞建模为具有独立状态(例如位置、周期状态)和过程(例如运动性、分泌)的智能体;参见图1A。每个细胞智能体都会对其微环境中的刺激(信号)做出反应,从而导致其行为发生变化(图1B)。
PhysiCell以前的实现方式局限于预定义的模型和相互作用,或者要求用户具备生物学、数学和计算机科学等多个领域的专业知识,才能手动编写具有定制化细胞智能体、刺激和相互作用的模型。在这里,我们通过扩展PhysiCell软件,将智能体和刺激编码为人类可读的语句,然后将其解析为ABM,从而简化了这种编码过程。
简而言之,这种抽象是通过以语法形式编写细胞假设来实现的,这些假设将细胞行为反应与信号相关联,并且可以转换为数学和可执行代码,如下所述(例如图1C中的典型规则)。在这种假设语法中,细胞行为和刺激被表示为名词,它们的调控关系被表示为动词,而参数则对这些关系进行量化。假设可以来自多种来源,包括领域专业知识、先前文献的挖掘以及转录组学和其他数据的分析。由于采用统一的知识表示方式,所有这些规则都可以兼容地整合到数学模型中。此外,使用通俗语言描述细胞表型还有助于将ABM变量直接映射到单细胞和空间多组学数据集分析中推断出的细胞标签上。
1\] Ghaffarizadeh A, Heiland R, Friedman S H, et al. PhysiCell: An open source physics-based cell simulator for 3-D multicellular systems\[J\]. PLoS computational biology, 2018 *** ** * ** *** 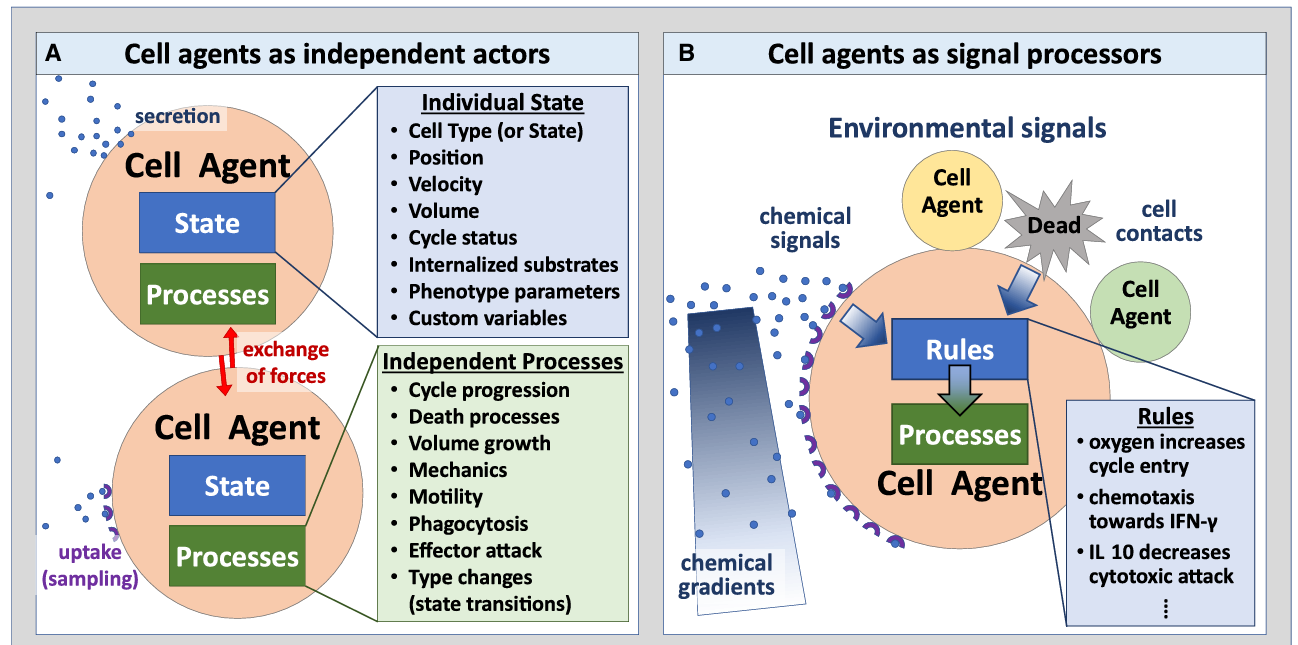 * 图(A)基于智能体的模型(ABMs,Agent Based Models)将细胞模拟为具有独立状态和过程的个体对象。secretion(分泌),uptake(吸收) * 图(B)细胞智能体利用规则处理其微环境中的生物物理信号(包括其他细胞),从而驱动自身行为的变化。这些规则基于我们的生物学假设。  * 图(C)细胞行为语法结合来自明确定义的词典(1和2)中的信号和行为,创建可解释的假设陈述(3),这些陈述可自动转换为数学模型(4),供计算机模型使用。 除了语法中包含的刺激因素和细胞类型,以及来自高通量分子数据集的可选初始条件外,基于智能体模型(ABMs)模拟的细胞行为还依赖于这些规则中方程的参数以及细胞表型的初始条件。虽然我们使用PhysiCell基于智能体的建模框架作为参考实现来构建这种语法,但它也可以转换到其他基于智能体的建模系统中。不过,在PhysiCell基础上构建这种假设语法的一个优势在于,它使我们能够利用大量的生化和生物物理参数,这些参数已在广泛的文献中得到量化和实验验证,并通过该建模框架的社区化开发得到了进一步完善。 假设语法会解析模型参数的数值变量。理想情况下,这些参数可以从文献中推断得出,或通过它们所要模拟的生物系统的实验数据进行量化。参数选择是ABMs的关键环节,因为它会显著影响模拟结果。尽管许多参数可以通过实验或从文献中估算得到,但生物系统的细胞和分子异质性可能因个体和环境不同而存在差异。在PhysiCell的整个开发过程中,作者通过多种方式改进了参数选择流程(例如贝叶斯方法、大规模参数空间扫描),为基于假设的语法和社区推广奠定了基础。 ## PhysiCell agent-based modeling framework PhysiCell是一个开源的、基于智能体的建模框架,由C++编写而成,可在多种桌面平台、云端以及高性能计算资源上运行。PhysiCell将每个细胞模拟为一个智能体,具有位置和体积、独立的生死速率,其运动由机械力平衡和有偏向的随机迁移共同驱动。在PhysiCell的较新版本中,智能体还能与内置的吞噬作用、效应器攻击、融合以及弹性细胞间黏附等模型进行交互。 PhysiCell与一个反应-扩散求解器(BioFVM)相结合,该求解器可模拟单个细胞智能体在其各自位置对可扩散因子的分泌和摄取(消耗),以及这些底物在细胞外空间的扩散和衰减过程。PhysiCell将其关键的细胞行为参数整合为一个表型对象,以便更简洁地表示。 建模人员通过编写自定义C++函数来模拟生物学假设,这些函数会根据细胞所处位置的条件(如与其他细胞的接触情况、机械压力以及信号因子的浓度和梯度等)动态改变细胞智能体的表型参数。**本文对PhysiCell进行了扩展,加入了内置函数,无需编写C++代码,就能解析用我们所提出的语法编写的规则,进而对细胞表型进行操作**。 ## 假设语法 ### 细胞行为 为构建这一语法,**我们需要对多细胞观测中常见的关键细胞行为以及相应的参考模型进行清晰的抽象**。在这一背景下,细胞行为指的是细胞层面的过程,例如细胞周期、死亡或吞噬作用。通常,每种行为都可以通过少量连续的表型参数来表示,这些参数描述了行为的速率、强度或频率。 在早期研究中,Sluka等人开发了细胞行为本体(CBO),将其作为描述单个细胞行为的受控词汇表。最近,作者与一个多学科联盟合作,将来自CBO和其他来源的行为进行扩展和结构化,整合到MultiCellDS(多细胞数据标准)中。具体而言,这项工作定义了一种细胞行为表型,它汇集了细胞行为的生物物理特征,并按功能层级组织:细胞周期、死亡、体积、力学特性、分泌(包括摄取)以及运动性。 自从将MultiCellDS作为预印本发布以来,作者已通过多种基于智能体的模拟和建模项目,对这种细胞行为研究方法进行了验证。基于近期的免疫学建模工作,作者对表型进行了扩展,将细胞间相互作用(吞噬作用、效应器攻击和融合)以及细胞类型间的转换(例如分化、转分化以及其他即使在去除外源信号后仍能持续存在的状态变化)也纳入其中。 ### 信号 信号是(通常为外源性,但有时为内源性)能够被细胞解读以驱动行为或状态变化的刺激或信息。在数学建模的语境中,信号是智能体规则的输入。作者广泛调研了来自癌症生物学、组织形态发生、免疫学以及微生物生态系统的数学和生物学模型,以归纳细胞行为规则的输入类别,这些输入通常包括化学因子、机械信号、细胞体积(例如,用于基于体积的周期检查点)、与其他细胞的物理接触、存活/死亡状态、当前模拟时间(用于触发事件)以及累积损伤(例如,来自效应器攻击)。 ### 状态 对于任何细胞类型T,作者构建简单的陈述来将单一行为B的变化与信号S关联起来:"在T中,S会增加/减少B(可附带可选参数)。" 这里的B是行为词典中一个明确定义的生物物理参数,S是信号词典中一个明确定义的生物物理变量,而可选参数则进一步明确反应的数学行为。例如: * In MCF-7 breast cancer cells, cisplatin increases apoptosis. (在MCF-7乳腺癌细胞中,顺铂会增加细胞凋亡) * In naive T cells, IL-10 decreases transition to CD8+ T cells.(在初始T细胞中,白细胞介素-10会减少向CD8⁺T细胞的转化) ### 数学表达:独立的规则 通过明确定义的行为B、信号S以及连接它们的语法,我们能够将人类可解释的细胞假设陈述唯一地映射到数学表达式上,这使得该语法既具有人类可解释性,又具备可计算性。每个单独的规则都将一个行为参数调节为信号 s s s的函数。给定一个响应函数 R R R,我们便可以将这个单独的规则用数学方式表示为函数 b ( s ) b(s) b(s): b ( s ) = b 0 + ( b M − b 0 ) R ( s ) , ( 1 ) b(s)=b_{0}+\\left(b_{M}-b_{0}\\right) R(s), (1) b(s)=b0+(bM−b0)R(s),(1) 其中, b 0 b_{0} b0是无信号时该参数的基准值, b M b_{M} bM是在强信号作用下该参数的最大变化值。默认情况下,我们采用S形(希尔)响应函数 R R R,这是因为它在信号网络模型和药效动力学中应用广泛,并且能在0(无响应)到1(最大响应)之间平滑变化。不过,也可以使用有上限的线性响应函数(在0到1之间变化)和阶跃函数。典型规则可参见图1C。 ### 通用的数学表达:多规则 完整的数学公式允许将新假设直接添加到模型中,而无需修改先前的假设,这使得该框架在获取新知识时具有可扩展性和可伸缩性。假设某一行为B(及其相应的行为参数b)由多个规则控制,这些规则分别受促进性(上调性)信号u和抑制性(下调性)信号d的影响: 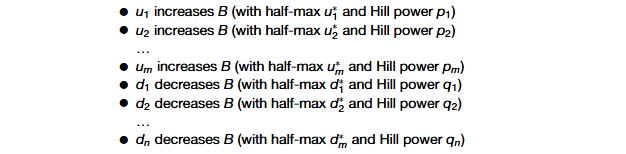 在此,令 b M b_{M} bM为行为参数 b b b的最大值(在上调信号 u u u的联合影响下),令 b 0 b_{0} b0为其在无信号时的基准值,令 b m b_{m} bm为其最小值(在下调信号 d d d 的联合影响下)。 与先前的多变量响应函数类似,我们将总上调响应定义为: U = H M ( u ; u h a l f , p ) = ( u 1 u 1 ∗ ) p 1 + ( u 2 u 2 ∗ ) p 2 + . . . + ( u m u m ∗ ) p m 1 + ( u 1 u 1 ∗ ) p 1 + ( u 2 u 2 ∗ ) p 2 + . . . + ( u m u m ∗ ) p m U=H_{M}\\left(u ; u_{half }, p\\right)=\\frac{\\left(\\frac{u_{1}}{u_{1}\^{\*}}\\right)\^{p_{1}}+\\left(\\frac{u_{2}}{u_{2}\^{\*}}\\right)\^{p_{2}}+...+\\left(\\frac{u_{m}}{u_{m}\^{\*}}\\right)\^{p_{m}}}{1+\\left(\\frac{u_{1}}{u_{1}\^{\*}}\\right)\^{p_{1}}+\\left(\\frac{u_{2}}{u_{2}\^{\*}}\\right)\^{p_{2}}+...+\\left(\\frac{u_{m}}{u_{m}\^{\*}}\\right)\^{p_{m}}} U=HM(u;uhalf,p)=1+(u1∗u1)p1+(u2∗u2)p2+...+(um∗um)pm(u1∗u1)p1+(u2∗u2)p2+...+(um∗um)pm 总下调响应定义为: D = H M ( d ; d h a l f , q ) = ( d 1 d 1 ∗ ) q 1 + ( d 2 d 2 ∗ ) q 2 + . . . + ( d n d n ∗ ) q n 1 + ( d 1 d 1 ∗ ) q 1 + ( d 2 d 2 ∗ ) q 2 + . . . + ( d n d n ∗ ) q n . D=H_{M}\\left(d ; d_{half }, q\\right)=\\frac{\\left(\\frac{d_{1}}{d_{1}\^{\*}}\\right)\^{q_{1}}+\\left(\\frac{d_{2}}{d_{2}\^{\*}}\\right)\^{q_{2}}+...+\\left(\\frac{d_{n}}{d_{n}\^{\*}}\\right)\^{q_{n}}}{1+\\left(\\frac{d_{1}}{d_{1}\^{\*}}\\right)\^{q_{1}}+\\left(\\frac{d_{2}}{d_{2}\^{\*}}\\right)\^{q_{2}}+...+\\left(\\frac{d_{n}}{d_{n}\^{\*}}\\right)\^{q_{n}}} . D=HM(d;dhalf,q)=1+(d1∗d1)q1+(d2∗d2)q2+...+(dn∗dn)qn(d1∗d1)q1+(d2∗d2)q2+...+(dn∗dn)qn. 通过在非线性上调响应 U U U和下调响应 D D D中进行双线性插值,将行为参数的整体响应组合如下: b ( u , d ) = ( 1 − D ) ⋅ \[ ( 1 − U ) ⋅ b 0 + U ⋅ b M \] + D ⋅ b m b(u, d)=(1-D) \\cdot\\left\[(1-U) \\cdot b_{0}+U \\cdot b_{M}\\right\]+D \\cdot b_{m} b(u,d)=(1−D)⋅\[(1−U)⋅b0+U⋅bM\]+D⋅bm 注意: * 当仅存在单一上调信号(或单一下调信号)时, b ( u , d ) b(u,d) b(u,d)会简化为系统生物学和药效动力学研究中使用的希尔响应曲线 b ( u ) b(u) b(u)或 b ( d ) b(d) b(d)。 * 通常情况下,上调信号的组合会设定该参数的"目标"值,而这一目标值随后可能会受到下调信号组合的抑制。 * U U U和 D D D在0-1之间,表示上调和下调的程度,比如 D D D越大,行为 b b b的下降幅度越大。 ### PhysiCell规则的实现与参数化 为了在PhysiCell中实现这些规则,用户需要生成一个CSV文件,其中每一行代表一条单独的规则,列则对应语法的特定元素。此类行的结构如下: 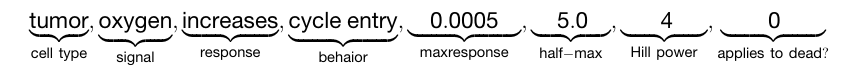 PhysiCell Studio提供的图形用户界面(GUI)简化了符合该框架的CSV文件的创建过程。在这个GUI中,用户还能交互式地可视化所有规则,以评估它们对不同输入信号和参数值的敏感性。 工具集还包括一个用于分析PhysiCell模型的Python包,功能涵盖敏感性分析、校准、模型选择和验证。这些不确定性量化(UQ)任务对于理解生物学和数学层面的变异性如何影响模型行为至关重要。重要的是,语法框架的加入使我们能够为终端用户提供这些功能,而无需他们编写定制的C++代码或XML解析器。为助力提高可重复性,在初始解析后,以HTML和文本格式生成并保存所有规则的完整描述。 ## 实验设置 ### 初始化 另一个关键的模型输入是ABM(基于智能体的模型)模拟中存在的细胞类型的初始化以及这些细胞智能体的初始位置。**PhysiCell允许用户在环境中随机初始化细胞,或者通过提供一个包含细胞位置的用户创建文件来进行初始化**。这种假设语法的一个优势在于,细胞智能体被赋予了人类可解释的名称,从而在智能体与经典单细胞及空间分子分析中定义的细胞marker之间建立了一一对应的映射关系。 为了利用这种映射关系,作者使用来自生物信息学数据集的细胞类型注释来设定模型中所包含细胞类型的相对丰度。如果数据还包含空间坐标,会使用仿射线性变换在模拟域中定位细胞。默认情况下,细胞的放置会填满整个模拟域,同时保持数据的纵横比。