数学分析栈的出栈顺序：从算法判断到数学本质（卡特兰数初探）

大家好！今天我们来聊聊栈的一个经典问题 ------如何判断弹出序列是否合法，以及背后更有意思的数学规律：为什么 n 个元素的合法出栈序列数是卡特兰数？内容会尽量通俗，搭配代码和示意图，适合刚接触栈或者想深入理解其数学逻辑的朋友。

一、基础问题：怎么判断弹出序列是否合法？

先从一道经典算法题入手，这题在牛客网、LeetCode 都很常见，题目描述如下：

输入两个整数序列，第一个是栈的压入顺序（所有数字不重复），请判断第二个序列是否可能是该栈的弹出顺序。示例 1：压入 [1,2,3,4,5]，弹出 [4,5,3,2,1] → 合法（返回 true）示例 2：压入 [1,2,3,4,5]，弹出 [4,3,5,1,2] → 不合法（返回 false）

1.1 常规解法：模拟栈操作

最直观的思路是 "复现" 栈的压入和弹出过程，步骤很简单：

遍历压入序列，把元素逐个压入栈；
每次压入后，检查栈顶元素是否和当前弹出序列的 "待弹出元素"（用指针标记）一致；
如果一致，就弹出栈顶，并移动弹出指针；
遍历结束后，若栈为空，说明所有元素都按顺序弹出，序列合法；否则不合法。

代码实现（C++）

cpp

复制代码

#include <vector>
#include <stack>
using namespace std;

bool IsPoporder(vector<int>& pushV, vector<int>& popV) {
    size_t popIdx = 0;  // 标记弹出序列的当前位置
    stack<int> st;      // 模拟用的栈
    
    // 遍历压入序列，逐个压栈
    for (auto& num : pushV) {
        st.push(num);
        
        // 栈顶匹配则弹出，直到栈空或不匹配
        while (!st.empty() && st.top() == popV[popIdx]) {
            st.pop();
            popIdx++;  // 移动弹出指针
        }
    }
    
    // 栈空 → 所有元素都合法弹出
    return st.empty();
}

1.2 模拟过程示意图（建议配图）

以示例 1 压入[1,2,3,4,5]，弹出[4,5,3,2,1] 为例，用表格展示每一步的变化：

步骤	压入元素	栈内元素	弹出指针 popIdx	栈顶是否匹配 popV [popIdx]	操作后栈内元素	操作后 popIdx
1	1	[1]	0	1≠4 → 不匹配	[1]	0
2	2	[1,2]	0	2≠4 → 不匹配	[1,2]	0
3	3	[1,2,3]	0	3≠4 → 不匹配	[1,2,3]	0
4	4	[1,2,3,4]	0	4=4 → 匹配	[1,2,3]	1
5	5	[1,2,3,5]	1	5=5 → 匹配	[1,2,3]	2
6	压入结束	[1,2,3]	2	3=3 → 匹配	[1,2]	3
7	-	[1,2]	3	2=2 → 匹配	[1]	4
8	-	[1]	4	1=1 → 匹配	[]	5

最终栈为空，返回true。如果是示例 2，最后栈会残留元素，返回false。

二、深入观察：出栈序列的隐藏规律

模拟法能解决问题，但如果笔试时没有编译器，能不能快速口算判断？我在分析多个按照顺序入栈的例子后，发现了一个关键规律：

如果入栈是顺序入栈，出栈序列中，任意元素后面比它小的元素，必须保持严格逆序。

2.1 用例子验证规律

例子 1：合法序列 [4,5,3,2,1]

看元素 4：后面比它小的元素是 [3,2,1] → 逆序（3>2>1），符合；
看元素 5：后面比它小的元素是 [3,2,1] → 逆序，符合；
看元素 3：后面比它小的是 [2,1] → 逆序，符合；
所有元素都满足，所以合法。

例子 2：不合法序列 [4,3,5,1,2]

重点看元素 5：后面比它小的元素是 [1,2] → 顺序（1<2），不符合规律；
因此直接判断不合法，和题目结果一致。

再举个合法例子：[3,4,5,2,1]

元素 3 后面比它小的是 [2,1] → 逆序；
元素 4 后面比它小的是 [2,1] → 逆序；
元素 5 后面比它小的是 [2,1] → 逆序；
符合规律，确实是合法出栈序列。

2.2 规律的本质：为什么会这样？

栈的核心是 "先进后出"（LIFO）。假设元素 A 比元素 B 先压入栈，若 A 还没弹出时 B 就弹出了，那么 A 必须在 B 之后弹出（因为 A 在 B 下面）。

对应到规律：如果元素 X 后面有比它小的元素 Y（Y 比 X 先压入），那么所有比 X 小且在 Y 之后压入的元素 Z，必须在 Y 之前弹出 ------ 否则就违反了 "先进后出"，这就是 "严格逆序" 的由来。

三、基于规律的判断代码实现

既然规律成立，我们可以换一种思路写判断代码：先把压入序列的 "数值" 映射到 "压入顺序下标"（比如压入 [2,3,4,5,1]，则 2 的下标是 0，3 是 1，...，1 是 4），再检查弹出序列对应的下标是否满足 "任意元素后比它小的元素严格逆序"。

代码实现（C++）

cpp

复制代码

#include <vector>
#include <unordered_map>
using namespace std;

bool IsPoporderByRule(vector<int>& pushV, vector<int>& popV) {
    // 1. 建立"数值→压入下标"的映射，将问题转为"有序下标"的判断
    unordered_map<int, int> valToIdx;
    for (int i = 0; i < pushV.size(); ++i) {
        valToIdx[pushV[i]] = i;
        // 若弹出序列有压入序列没有的数，直接不合法
        if (valToIdx.find(popV[i]) == valToIdx.end()) {
            return false;
        }
    }
    
    // 2. 把弹出序列转为对应的"压入下标"序列
    vector<int> popIdx;
    for (int num : popV) {
        popIdx.push_back(valToIdx[num]);
    }
    
    // 3. 检查规律：任意元素后比它小的元素是否严格逆序
    int n = popIdx.size();
    for (int i = 0; i < n; ++i) {
        // 遍历当前元素后面的所有元素
        for (int j = i + 1; j < n; ++j) {
            // 若j是比i小的下标，检查后面是否有"比i小但比j大"的下标（破坏逆序）
            if (popIdx[j] < popIdx[i]) {
                for (int k = j + 1; k < n; ++k) {
                    if (popIdx[k] < popIdx[i] && popIdx[k] > popIdx[j]) {
                        return false;  // 存在非逆序，不合法
                    }
                }
            }
        }
    }
    
    return true;
}

代码逻辑很简单：通过下标映射，把任意压入序列的问题，转化为 "1,2,3,...n" 有序压入的问题，再用规律验证即可。

四、探索出栈序列总数：邂逅卡特兰数

解决了 "判断合法性"，新问题来了：n 个元素的合法出栈序列有多少种？

比如：

n=1 → 1 种（[1]）；
n=2 → 2 种（[1,2]、[2,1]）；
n=3 → 5 种（[123,132,213,231,321]）；
n=4 → 14 种；n=5 → 42 种...

4.1 我的失败推导尝试

我曾想基于 "严格逆序" 规律推导总数：以 n=5 为例，把最大元素 5 放在不同位置（比如第 1 位、第 2 位... 第 5 位），认为 5 后面的元素必须逆序，前面的元素符合卡特兰数。

比如假设 5 在第 3 位，前面有 2 个元素（符合卡特兰数 C₂=2），从 4 个元素选 2 个放在前面（组合数 C₄²=6），总数就是 2×6=12。但实际计算时发现，这样会多算不合法的序列（比如 [3,1,5,4,2]，1 和 2 的顺序破坏了逆序），推导以失败告终。

4.2 卡特兰数：答案的数学本质

后来才知道，这个问题的答案早就被数学家卡特兰解决了 ------n 个元素的合法出栈序列数，等于第 n 个卡特兰数，其通项公式为：

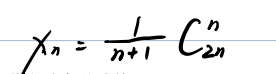
其中 C是组合数，表示从 2n 个元素中选 n 个的方案数。

我们验证一下：

n=1：结果是1→ 正确；
n=2：结果是2 → 正确；
n=3：结果是5→ 正确；
n=5：结果是42 → 正确。

4.3 卡特兰数的更多应用（拓展）

卡特兰数不只是栈的专利，它还出现在很多场景：

括号匹配：n 对括号的合法匹配数（如 n=2：()()、(()) → 2 种）；
二叉树计数：n 个节点的不同二叉树结构数（n=2：2 种）；
路径规划：从 (0,0) 到 (n,n) 不穿过对角线的路径数。

这就是数学的魅力 ------ 不同问题背后，可能藏着同一个数学规律。

五、总结

判断弹出序列合法 ：两种方法
- 模拟栈操作：效率 O (n)，适合编程实现；
- 规律判断：基于 "元素后小元素严格逆序"，适合快速口算。
出栈序列总数：第 n 个卡特兰数，公式是

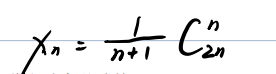
数学本质：栈的 "先进后出" 规则，最终转化为卡特兰数的计数问题，体现了算法与数学的紧密联系。