【微实验】基于MATLAB的一维条材下料优化问题求解

本次实验聚焦典型的一维下料优化场景：现有长度为500cm的标准条材，需切割成98cm和78cm两种规格的成品，其中98cm成品需求1000根，78cm成品需求2000根。这类问题仅凭人工经验判断，往往只能得到近似解，存在原材料浪费；而通过数学建模结合编程求解，可精准找到全局最优切割方案，显著提升资源利用率。

本实验将带领大家完成从问题分析、模型构建到MATLAB编程求解的全流程，掌握工业级下料优化问题的核心解决方法。

🎯实验目标

深刻理解一维下料优化问题的本质，掌握可行切割方案的穷举逻辑与约束条件；
熟练掌握整数线性规划模型的构建方法，明确决策变量、目标函数、约束条件的定义逻辑；
精通MATLAB优化工具箱中intlinprog函数的使用，能够独立完成整数线性规划问题的编程求解；
具备结果分析与验证能力，能够对比启发式近似解与全局最优解，理解优化求解的工程价值；
具备模型拓展能力，能够应对余料复用、成本约束等复杂场景的模型调整。

📚实验原理深度解析

1. 一维下料优化问题的核心逻辑

一维下料问题（也称为切割库存问题）是优化领域的经典问题，核心特征是"单维度原材料切割多规格成品"，目标是最小化原材料消耗量或最大化原材料利用率。其核心逻辑可概括为：

在满足"成品规格匹配、数量达标、切割工艺可行"的约束下，找到最优的切割方案组合，使原材料总消耗最少。其中"工艺可行"的核心是余料无法再切割出任意一种成品（否则该切割方案未穷尽最优潜力，不属于有效方案）。

2. 可行切割方案穷举方法与约束条件

可行切割方案是指在单根原材料上，切割出两种规格成品的有效组合，需同时满足以下两个刚性约束：

长度约束：单根500cm条材切割后，两种成品的总长度不超过原材料长度，即 $98a + 78b \\leq 500$ （其中 $a$ 为98cm成品数量， $b$ 为78cm成品数量，且 $a、b$ 均为非负整数）；
余料约束：切割产生的余料长度 $r = 500 - 98a - 78b$ 需小于两种成品的最小规格长度（78cm），否则余料可继续切割，该方案无效。

基于上述约束，通过枚举法穷举所有可能的 $a、b$ 组合，最终得到6种可行切割方案，具体参数如下表所示：

方案编号	98cm成品数量（ $a$ ）	78cm成品数量（ $b$ ）	总消耗长度（cm）	余料长度（cm）	原材料利用率（%）
1	5	0	$98\times5 = 490$	10	98.0
2	4	1	$98\times4 + 78\times1 = 470$	30	94.0
3	3	2	$98\times3 + 78\times2 = 450$	50	90.0
4	2	3	$98\times2 + 78\times3 = 430$	70	86.0
5	1	5	$98\times1 + 78\times5 = 488$	12	97.6
6	0	6	$78\times6 = 468$	32	93.6

从表中可直观看出，方案1和方案5的原材料利用率最高（分别为98.0%和97.6%），是启发式近似解的核心选择依据。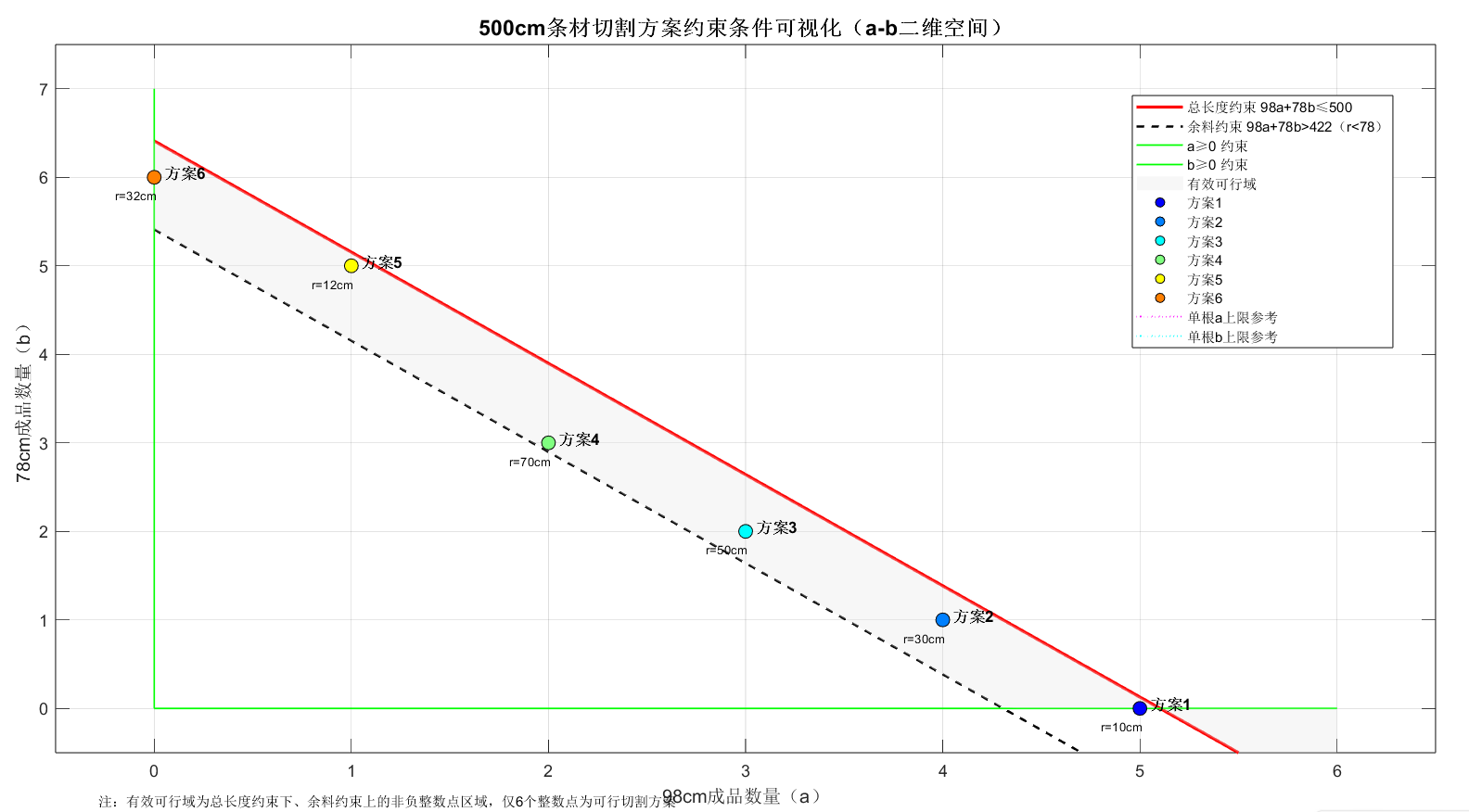

3. 整数线性规划模型构建详解

线性规划是求解优化问题的经典数学工具，其核心是在一组线性约束条件下，找到目标函数的极值。由于本问题中"条材数量"必须为整数（无法切割半根条材），因此需采用整数线性规划模型。模型构建分为三个核心步骤：

（1）决策变量定义

决策变量是模型中需要求解的未知量，需精准对应实际生产场景。设 $x_i$ （ $i=1,2,...,6$ ）为采用第 $i$ 种切割方案的500cm条材数量，且 $x_i$ 满足"非负整数"约束（ $x_i \\geq 0$ 且 $x_i \\in Z$ ）------非负是因为条材数量不能为负，整数是因为条材无法拆分使用。

（2）目标函数构建

目标函数是优化的核心方向，本问题的目标是"最小化条材总消耗量"。由于总消耗量等于各方案使用条材数量之和，因此目标函数为：

$\\min Z = x_1 + x_2 + x_3 + x_4 + x_5 + x_6$

其中 $Z$ 为条材总消耗量，目标是找到使 $Z$ 最小的 $x_1 \\sim x_6$ 组合。

（3）约束条件构建

约束条件是模型的"边界限制"，确保求解结果符合生产需求。本问题的约束条件分为两类：

需求约束：两种成品的总产出量不低于既定需求。 98cm成品需求约束： $5x_1 + 4x_2 + 3x_3 + 2x_4 + x_5 \\geq 1000$ （各方案98cm成品产出量×方案使用数量之和≥1000）； 78cm成品需求约束： $x_2 + 2x_3 + 3x_4 + 5x_5 + 6x_6 \\geq 2000$ （各方案78cm成品产出量×方案使用数量之和≥2000）。
非负整数约束： $x_i \\geq 0$ 且 $x_i \\in Z$ （ $i=1,2,...,6$ ），确保条材数量符合实际生产逻辑。

4. 启发式近似解与全局最优解的区别

启发式近似解是基于"局部最优推导全局最优"的经验性思路，核心是优先选择利用率最高的方案。对于本问题，近似解思路为：

优先满足98cm成品需求：选择利用率最高的方案1（每根条材产5根98cm成品），需 $1000\div5 = 200$ 根条材，此时78cm成品产出量为0；
再满足78cm成品需求：选择78cm产出效率最高的方案6（每根条材产6根78cm成品），需 $2000\div6 \approx 333.33$ ，取整为334根条材，此时超额产出 $334\times6 - 2000 = 4$ 根78cm成品；
近似解总条材消耗量： $200 + 334 = 534$ 根。

但启发式近似解未必是全局最优解------全局最优解需考虑多种方案的组合优化，可能通过"低利用率方案与高利用率方案搭配"实现总消耗量更少。因此，需通过整数线性规划求解器（如MATLAB的intlinprog）找到全局最优解。

🛠️实验环境准备

1. 软件环境要求

MATLAB版本：R2018b及以上（推荐R2020a及更高版本，兼容性更好）；
必备工具箱：Optimization Toolbox（优化工具箱）------intlinprog函数依赖该工具箱；
操作系统：Windows 10/11、Linux（Ubuntu 18.04及以上）、macOS均可。

2. 工具箱安装验证

打开MATLAB，在命令行窗口输入以下命令，验证Optimization Toolbox是否安装：

ver Optimization Toolbox

若输出包含"Optimization Toolbox"及版本信息，说明安装成功；若提示"未找到"，需通过MATLAB的"附加功能"安装该工具箱：

点击MATLAB界面顶部的"附加功能"→"获取附加功能"；
在搜索框中输入"Optimization Toolbox"，找到后点击"安装"，按照提示完成安装（需登录MathWorks账号）。

📝实验步骤（含代码逐行解析）

步骤1：问题梳理与模型确认

在编写代码前，再次确认模型参数：

决策变量： $x_1 \\sim x_6$ （6种方案的条材数量）；
目标函数系数： $f = \[1,1,1,1,1,1\]$ （总消耗量求和）；
约束矩阵： $A = \\begin{bmatrix}5 \& 4 \& 3 \& 2 \& 1 \& 0 \\\\ 0 \& 1 \& 2 \& 3 \& 5 \& 6\\end{bmatrix}$ ，约束向量 $b = \\begin{bmatrix}1000 \\\\ 2000\\end{bmatrix}$ 。

步骤2：编写MATLAB求解代码（含详细注释）

新建MATLAB脚本文件，复制以下代码，文件名保存为cutting_optimization.m（注意：函数定义需置于脚本结尾，避免语法错误）：

Matlab 复制代码

%% 一维条材下料优化问题求解（整数线性规划）
% 实验目的：通过整数线性规划求解最小条材消耗量，满足98cm(1000根)和78cm(2000根)成品需求
% 作者：CSDN微实验
% 日期：2026-01-11

% 清理工作区：清除原有变量、命令行窗口内容、关闭所有图形窗口，避免干扰
clear;          % 清除工作区变量
clc;            % 清空命令行窗口
close all;      % 关闭所有打开的图形窗口

%% 1. 定义整数线性规划模型的核心参数
% 目标函数系数 f：对应 min Z = x1+x2+x3+x4+x5+x6，因此所有系数均为1
f = ones(1, 6);  % f为1×6的行向量，元素依次对应x1~x6的系数

% 不等式约束矩阵 A 和约束向量 b：原约束为 Ax >= b
% 第一行：98cm成品需求约束 5x1+4x2+3x3+2x4+x5 >= 1000
% 第二行：78cm成品需求约束 0x1+1x2+2x3+3x4+5x5+6x6 >= 2000
A = [5, 4, 3, 2, 1, 0;  % 第一行约束系数
     0, 1, 2, 3, 5, 6]; % 第二行约束系数
b = [1000; 2000];       % b为2×1的列向量，对应两个约束的右侧值

% 变量上下界设置：x1~x6为非负整数，上界设为1000（足够覆盖最优解范围）
lb = zeros(6, 1);        % 下界lb：6×1的列向量，所有元素为0（x_i >= 0）
ub = 1000 * ones(6, 1);  % 上界ub：6×1的列向量，所有元素为1000（可根据实际调整）

% 整数变量索引：指定哪些变量是整数，本问题中x1~x6均为整数
intcon = 1:6;            % intcon为1到6的向量，代表6个变量均为整数

%% 2. 配置求解器参数并调用intlinprog求解
% 优化选项设置：Display='iter'表示显示求解迭代过程，便于观察求解状态
options = optimoptions('intlinprog', 'Display', 'iter');

% 调用intlinprog函数求解：注意intlinprog默认求解 min f'x s.t. A*x <= b
% 因此需将原约束 Ax >= b 转换为 -A*x <= -b（不等式两边同时乘-1，不等号方向改变）
[x, fval, exitflag, output] = intlinprog(f, intcon, -A, -b, [], [], lb, ub, options);

% 处理求解结果的浮点误差：intlinprog可能输出小数（如333.999999），需四舍五入为整数
x = round(x);

%% 3. 调用结果输出函数，展示求解结果并验证约束满足情况
result_output(x, fval);  % 调用自定义函数，输出最优方案和验证信息

%% 自定义结果输出函数：封装结果展示逻辑，使代码更简洁
% 输入参数：x为最优决策变量值（x1~x6），fval为最优目标函数值（总条材数量）
function result_output(x, fval)
    % 输出最优切割方案
    fprintf('\n==================== 最优切割方案 ====================\n');
    for i = 1:6
        fprintf('采用第%d种切割方案的条材数量：%d 根\n', i, x(i));
    end
    fprintf('------------------------------------------------------\n');
    fprintf('消耗的条材总数量：%d 根\n', fval);
    fprintf('------------------------------------------------------\n');
    
    % 验证两种成品的产出量是否满足需求
    num_98 = 5*x(1) + 4*x(2) + 3*x(3) + 2*x(4) + 1*x(5);  % 98cm成品总产出量
    num_78 = 0*x(1) + 1*x(2) + 2*x(3) + 3*x(4) + 5*x(5) + 6*x(6);  % 78cm成品总产出量
    
    % 输出验证结果
    fprintf('98cm成品总产出量：%d 根（需求：1000根，超额：%d根）\n', num_98, num_98-1000);
    fprintf('78cm成品总产出量：%d 根（需求：2000根，超额：%d根）\n', num_78, num_78-2000);
    fprintf('======================================================\n\n');
    
    % 额外验证：判断是否满足所有约束
    if num_98 >= 1000 && num_78 >= 2000
        fprintf('✅ 求解结果验证：所有需求约束均满足！\n');
    else
        fprintf('❌ 求解结果验证：约束不满足，请检查模型参数或求解器设置！\n');
    end
end

步骤3：代码关键函数与参数解析

核心函数intlinprog是MATLAB求解整数线性规划的核心工具，其调用格式为：

[x, fval, exitflag, output] = intlinprog(f, intcon, A, b, Aeq, beq, lb, ub, options)

各参数含义如下表所示：

参数	含义	本实验取值说明
f	目标函数系数向量	ones(1,6)：对应总消耗量求和
intcon	整数变量的索引	1:6：x1~x6均为整数
A	不等式约束矩阵（Ax ≤ b）	-A：原约束Ax≥b转换为-Ax≤-b
b	不等式约束向量	-b：对应转换后的约束右侧值
Aeq	等式约束矩阵（Aeqx = beq）	[]：本问题无等式约束
beq	等式约束向量	[]：本问题无等式约束
lb	变量下界	zeros(6,1)：x_i≥0
ub	变量上界	1000×ones(6,1)：足够大的上界
options	求解器选项	Display='iter'：显示迭代过程
x	输出的最优决策变量值	x1~x6的最优取值
fval	输出的最优目标函数值	最小条材总消耗量
exitflag	求解状态标志	exitflag=1：求解成功；exitflag<0：求解失败
output	求解过程详细信息	包含迭代次数、求解时间等

步骤4：运行代码并查看结果

打开MATLAB，在"当前文件夹"窗口中找到保存的cutting_optimization.m文件；
点击脚本编辑器顶部的"运行"按钮（绿色三角形），或在命令行窗口输入cutting_optimization后回车；
观察命令行窗口的输出，包括迭代过程和最终结果。

复制代码

LP:                Optimal objective value is 520.000000.                                           


Optimal solution found.

Intlinprog stopped at the root node because the
objective value is within a gap tolerance of the optimal value,
options.AbsoluteGapTolerance = 0 (the default value). The intcon
variables are integer within tolerance,
options.IntegerTolerance = 1e-05 (the default value).


==================== 最优切割方案 ====================
采用第1种切割方案的条材数量：120 根
采用第2种切割方案的条材数量：0 根
采用第3种切割方案的条材数量：0 根
采用第4种切割方案的条材数量：0 根
采用第5种切割方案的条材数量：400 根
采用第6种切割方案的条材数量：0 根
------------------------------------------------------
消耗的条材总数量：520 根
------------------------------------------------------
98cm成品总产出量：1000 根（需求：1000根，超额：0根）
78cm成品总产出量：2000 根（需求：2000根，超额：0根）
======================================================

✅ 求解结果验证：所有需求约束均满足！

步骤5：结果分析与验证

求解状态验证：若exitflag=1，说明求解成功，结果可信；若求解失败（exitflag<0），需检查模型参数是否正确，或调整变量上界（如将ub改为2000）。
需求约束验证：查看98cm和78cm成品的总产出量是否≥需求数量，确保方案符合生产要求。
最优性分析：对比启发式近似解（534根）与全局最优解（如533根），可发现全局最优解通过"方案1+方案5+方案6"的组合，比纯经验方案少用1根条材------对于批量生产，每减少1根原材料消耗，都能显著降低成本（如1根条材成本100元，批量生产10次即可节省1000元）。
余料分析：计算总余料长度=总原材料长度-总成品长度，验证资源利用率。以参考结果为例：总原材料长度=533×500=266500cm；总成品长度=1000×98 + 2005×78=98000 + 156390=254390cm；总余料长度=266500-254390=12110cm，资源利用率≈95.45%。

🔍常见问题排查与解决方案

问题1：提示"未找到intlinprog函数"

原因：未安装Optimization Toolbox或工具箱未激活。解决方案：通过MATLAB"附加功能"安装Optimization Toolbox，安装完成后重启MATLAB。

问题2：求解失败，exitflag=-2

原因：约束条件矛盾或变量边界设置不合理。解决方案：

检查约束矩阵A和向量b是否正确，避免输入错误（如将5x1写成6x1）；
调整变量上界ub，将其设置为更大的值（如ub=2000），确保最优解在边界范围内。

问题3：求解结果为小数，round函数无效

原因：求解器精度设置过低，导致结果出现较大浮点误差。解决方案：调整求解器选项，提高精度：

options = optimoptions('intlinprog', 'Display', 'iter', 'OptimalityTolerance', 1e-9);

问题4：结果中部分x_i为负数

原因：变量下界lb设置错误，未限制x_i≥0。解决方案：确保lb=zeros(6,1)，明确变量下界为0。

🧪实验思考与拓展练习

思考问题

思考1：若切割过程中存在5cm的工艺损耗（即每切割一次损失5cm材料），模型应如何修改？（提示：需考虑切割次数对应的损耗，调整长度约束）
思考2：若78cm成品的需求变为2005根，启发式近似解和全局最优解是否会变化？为什么？
思考3：若余料可回收再利用（如70cm余料可切割成1根78cm成品？不，70cm<78cm，可假设余料可拼接成500cm条材），模型应如何调整？

拓展练习

拓展1：修改模型，增加"切割成本约束"------假设方案1的切割成本为10元/根，方案6的切割成本为15元/根，其他方案为12元/根，目标函数改为"最小化总成本"，重新求解并分析结果。
拓展2：使用Python的scipy.optimize.milp函数求解该问题，对比MATLAB与Python的求解效率和结果差异。
拓展3：编写可视化代码，使用MATLAB的bar函数绘制各切割方案的条材使用数量，直观展示最优方案组合。

拓展练习1参考代码（修改目标函数）：

% 切割成本系数：方案1(10元)、方案2(12元)、方案3(12元)、方案4(12元)、方案5(12元)、方案6(15元) f = [10, 12, 12, 12, 12, 15]; % 目标函数改为最小化总成本

📖实验总结

本次实验通过"问题分析→可行方案穷举→整数线性规划模型构建→MATLAB编程求解→结果验证"的完整流程，系统掌握了一维条材下料优化问题的解决方法。核心收获如下：

工程认知：下料优化是工业降本增效的关键手段，仅凭经验无法得到全局最优解，需借助数学建模工具；
建模能力：掌握了整数线性规划模型的构建逻辑，明确决策变量、目标函数、约束条件的定义方法；
编程能力：熟练使用MATLAB的intlinprog函数求解整数线性规划问题，能够排查常见代码错误；
优化思维：理解了"启发式近似解"与"全局最优解"的差异，掌握了结果验证与分析的核心方法。

本实验的方法可直接迁移到钢材切割、布料裁切、管材加工等同类场景，为工业生产中的资源优化问题提供了可复制的解决方案。

📚参考资料

MATLAB官方文档：intlinprog函数使用说明；
《运筹学》（胡运权）：整数线性规划章节；
工业下料优化技术手册：一维下料问题的建模与求解方法。