1.概念
多目标规划(Multi-Objective Optimization, MOO)是数学规划的一个分支,用于解决同时优化多个相互冲突的目标函数的问题。其核心在于寻找一组"帕累托最优解"(Pareto Optimal Solutions),即在没有其他解能同时改善所有目标的情况下,这些解是最优的。
多目标规划相比前面的单一目标规划,就是目标函数不止一个,前面只有一个目标函数,那么目标函数最小的时候就是答案。但是多目标规划目标函数不止一个,求出的答案也不是每一个目标函数都是最优
常见例题:
物流中心选址,需要同时满足运输成本和建设费用(选址)都较低
投资组合,需要风险尽可能小,收益尽可能大
2.解
1.解的类型
由于目标函数不止一个所以解有三种类型
|-----|-----------------------------------------------------------------|
| 最优解 | 所有目标函数都取到了最优(几乎不存在) |
| 有效解 | 使至少一个目标函数取到最小值但不是所有(如果是所有就是上一种情况) |
| 满意解 | 主要是从决策者的角度,根据决策者的偏好提出的,有的时候决策者要求低给出的要求不高,只要满足要求就认为可以接受,是满意解 |
对于绝大多数问题,决策者偏好的方案都是有效解
2.求解方法
求解之前要对目标函数去量纲,归一化
补充:
去量纲(无量纲化)
去量纲是将不同量纲或单位的特征转换为统一尺度,消除量纲对模型的影响。
归一化
归一化通常指将数据转换为单位范数或特定比例
|------------------|-------------------------------------------------|---------------------------------------------------------|
| 方法 | 核心 | 特点 |
| 线性加权法 | 将多个目标函数通过权重加权求和,转化为单目标优化问题。 | * 权重由决策者主观确定,导致结果可能因偏好不同而变化。 * 简单易行,但对权重敏感,可能遗漏非凸解。 |
| 约束法(主要目标法/参考目标法) | 选定一个主要目标优化,其他目标转化为约束条件(设定容许阈值)。 | * 通过调整阈值可生成不同的Pareto解。 * 需明确次要目标的可接受范围,对阈值设定敏感。 |
| 理想点法 | 以各单目标最优值为"理想值",最小化目标值与理想值的加权平方偏差。 | * 兼顾所有目标与理想值的接近程度,结果更均衡。 * 需预先计算单目标最优值,计算复杂度较高。 |
| 优先级法 | 按目标重要性分层,逐级优化:高优先级目标先最优,低优先级在不劣化高优先级的前提下优化。 | * 严格反映决策者的优先级顺序,但可能牺牲低优先级目标的性能。 * 适用于目标有明确先后次序的场景。 |
其中线性加权法简单常用
线性加权法就是对多目标函数进行加权组合,使其变成单目标规划
step1:确定权系数
step2:写出评价函数
step3:求评价函数最优值
注意:
注意:
1、要将多个目标函数统一 为最大化和最小化问题(不同的加"-")才可以进行加权组合
2、如果目标函数量纲不同,则需要对其进行标准化再进行加权,标准化的方法一般是且标函数除以某一个常量,该常量是这个目标函数的某个取值,具体取何值可根据经验确定
3、对多目标函数进行加权求和是,权重一般由该领域专家给定
3.例题
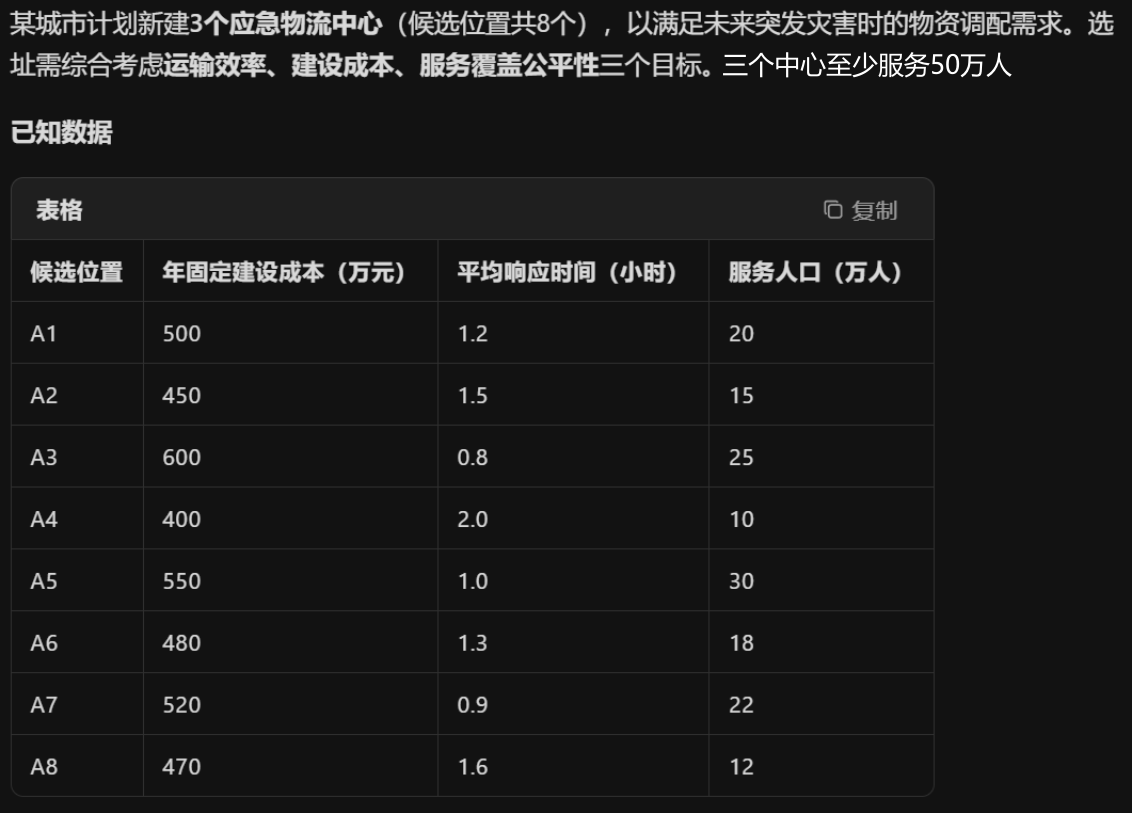
决策变量
设二元变量 xi∈{0,1},其中 xi=1 表示在位置 Ai 建设物流中心(i=1,2,...,8)。
 约束条件
约束条件
1.建设数量限制
2.覆盖人口下限
分析完后可以得到以下模型
然后对目标函数去除量纲并且加权

所以目标函数转化为
化简完成就是
原来的模型也就变成了这个
这个就是典型的线性规划了,用linprog求解
4.补充
敏感性分析概述
敏感性分析用于评估模型输出对输入参数变化的敏感程度,广泛应用于金融、工程、项目管理等领域。通过识别关键变量,帮助决策者优化资源分配或降低风险。
单变量敏感性分析
固定其他参数,仅改变一个输入变量,观察输出结果的变化。适用于参数间独立性较强的场景。
步骤示例:
- 选择目标变量(如净现值NPV)。
- 确定待测试的输入参数(如折现率、成本)。
- 在合理范围内调整单一参数值(如折现率从5%增至10%)。
- 记录输出结果并绘制敏感性曲线。
多变量敏感性分析
同时改变多个输入参数,分析其对输出的综合影响。常用方法包括蒙特卡洛模拟和方差分解法。
蒙特卡洛模拟步骤:
- 定义输入参数的概率分布(如正态分布、均匀分布)。
- 随机生成参数组合并计算输出结果。
- 通过统计方法(如相关系数、回归分析)量化敏感性
像上面用linprog之后就可以输入更多可能的权重,根据结果和需求来看是否是最佳结果