机器学习 ------ 决策树(Decision Tree)详细介绍
决策树是一种直观且易于解释的监督学习算法,广泛应用于分类和回归任务。它通过模拟人类决策过程,将复杂问题拆解为一系列简单的判断规则,最终形成类似 "树" 状的结构。以下从基础概念、原理、算法类型、优缺点及应用场景等方面展开详细介绍。
一、决策树的基础概念
1. 核心定义
决策树是一种基于树状结构进行决策的模型,每个节点代表对某个特征的判断,每条分支代表该判断的可能结果,叶子节点则代表最终的决策结果(分类任务中为类别,回归任务中为数值)。
2. 基本结构
- 根节点(Root Node):树的起点,包含所有样本数据,是第一个特征判断的起点。
- 内部节点(Internal Node):表示对某个特征的判断条件(如 "年龄是否> 30 岁"),每个内部节点会根据特征值分裂为多个子节点。
- 分支(Branch):连接节点的线段,代表特征判断的结果(如 "是" 或 "否")。
- 叶子节点(Leaf Node):树的终点,输出最终的预测结果(分类任务中为类别标签,回归任务中为预测值)。
示例 :用决策树判断 "是否购买电脑"
根节点:收入水平(高 / 中 / 低)→ 内部节点:年龄(<30/30-40/>40)→ 叶子节点:购买 / 不购买。
二、决策树的工作原理
决策树的核心是如何选择特征进行节点分裂,目标是通过分裂使子节点的 "纯度" 更高(即子节点中的样本尽可能属于同一类别或数值更集中)。具体流程如下:
1. 特征选择:如何分裂节点?
特征选择的关键是通过不纯度指标衡量分裂效果,常用指标包括:
(1)信息增益(Information Gain)------ ID3 算法
基于熵(Entropy) 计算,熵衡量样本集合的混乱程度,熵值越低,纯度越高。
- 熵的计算公式(针对分类任务):
对于样本集合D,若有k个类别,每个类别占比为pi,则熵为:
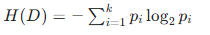
信息增益:分裂后子节点的熵与父节点熵的差值,即:
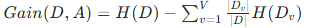
其中A为特征,Dv为特征A取第v个值的子样本集,信息增益越大,特征越优。
(2)信息增益率(Gain Ratio)------ C4.5 算法
解决信息增益偏向多值特征的问题(如 "身份证号" 这类特征分裂后熵极低,但无实际意义)。
信息增益率 = 信息增益 / 特征自身的熵(分裂信息)。
(3)基尼指数(Gini Index)------ CART 算法
衡量从样本中随机抽取两个样本,类别不同的概率,基尼指数越低,纯度越高。
计算公式:
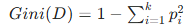
CART 算法通过最小化基尼指数选择特征。
(4)均方误差(MSE)------ 回归树
针对回归任务,用子节点样本的均方误差衡量分裂效果,MSE 越小越好:
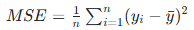
其中yˉ为子节点样本的均值。
2. 树的构建过程
- 从根节点开始,计算所有特征的不纯度指标(如信息增益)。
- 选择最优特征进行分裂,将样本分配到子节点。
- 对每个子节点重复步骤 1-2,直到满足停止条件:
- 子节点样本全部属于同一类别(分类)或数值方差小于阈值(回归)。
- 节点样本数小于最小分裂阈值。
- 树的深度达到预设最大值。
3. 剪枝:防止过拟合
决策树若完全生长可能导致过拟合(对训练数据拟合过好,泛化能力差),需通过剪枝优化:
- 预剪枝(Pre-pruning):在树构建过程中提前停止分裂(如限制深度、最小样本数)。
- 后剪枝(Post-pruning):先构建完整树,再移除对泛化能力无帮助的分支(如通过交叉验证判断分支是否保留)。
三、常见决策树算法对比
| 算法 | 任务类型 | 特征选择指标 | 树结构 | 优势 | 缺点 |
|---|---|---|---|---|---|
| ID3 | 分类 | 信息增益 | 多叉树 | 简单直观 | 不支持连续特征,易过拟合 |
| C4.5 | 分类 | 信息增益率 | 多叉树 | 支持连续特征、缺失值处理 | 计算复杂,不支持回归 |
| CART | 分类 / 回归 | 基尼指数(分类)、MSE(回归) | 二叉树 | 可处理分类和回归,效率高 | 对不平衡数据敏感 |
四、决策树的优缺点
优点
- 可解释性强:树结构直观,能清晰展示决策规则(如 "若年龄> 30 且收入高,则购买")。
- 无需特征预处理:对特征缩放、归一化不敏感,可直接处理类别型和数值型特征。
- 训练效率高:基于贪心算法,计算复杂度较低(尤其 CART 树)。
- 抗噪声能力较强:通过剪枝可减少噪声影响。
缺点
- 易过拟合:未剪枝的树可能过度拟合训练数据,泛化能力差。
- 对样本敏感:训练数据微小变化可能导致树结构大幅改变(稳定性差)。
- 偏向高维特征:信息增益等指标可能优先选择多值特征。
- 难以处理非线性关系:单个决策树对复杂数据的拟合能力有限(可通过集成学习弥补)。
五、决策树的扩展:集成学习
为解决单个决策树的局限性,衍生出集成学习方法,通过组合多个决策树提升性能:
- 随机森林(Random Forest):多个决策树的投票 / 平均,通过随机采样样本和特征降低方差。
- 梯度提升树(GBDT):迭代生成决策树,每个树修正前序树的误差,提升精度。
- XGBoost/LightGBM:优化的 GBDT 实现,效率和精度更优,广泛用于竞赛和工业界。
六、应用场景
决策树因其易解释性和实用性,在多个领域广泛应用:
- 金融风控:信用评分(如 "收入> 5 万且无逾期,则贷款批准")。
- 医疗诊断:疾病判断(根据症状特征逐步排查病因)。
- 客户分类:用户画像与行为预测(如 "高活跃度且消费频繁的用户为优质客户")。
- 工业质检:通过特征判断产品是否合格。
- 回归预测:房价预测、销量预测等(回归树)。
总结
决策树是一种简单高效的监督学习算法,核心是通过不纯度指标选择特征分裂节点,结合剪枝优化避免过拟合。尽管存在稳定性差等局限,但通过集成学习(如随机森林、GBDT)可显著提升性能,使其成为工业界和学术界的重要工具。理解决策树的原理是掌握集成学习的基础,也是机器学习入门的核心知识点之一。
用一个简单案例说明ID3的计算方法
数据如图所示
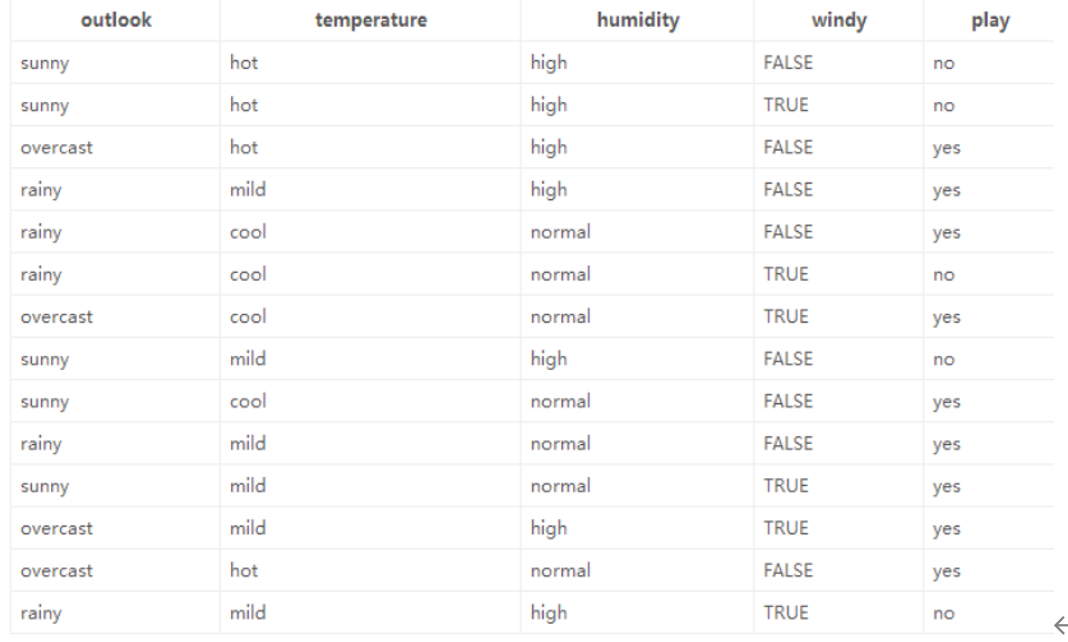
以下是使用 ID3 算法 构建决策树的详细计算过程,基于你提供的天气数据集(判断是否适合户外运动 play),步骤如下:
1. 数据集与目标
- 数据集 :包含 14 条样本,特征为
outlook(天气)、temperature(温度)、humidity(湿度)、windy(是否有风),标签为play(是否适合运动,yes/no)。 - 目标 :用 ID3 算法选择特征、构建决策树,实现对
play的分类。
2. ID3 核心思想:用 信息增益(Information Gain) 选择最优特征
信息增益公式:
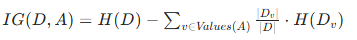
- H(D):数据集 D 的 经验熵(衡量标签不确定性)。
- H(Dv):特征 A 取值为 v 时子集 Dv 的经验熵。
- 信息增益越大,特征对分类结果的 "区分度" 越高,优先选它做决策节点。
3. 计算步骤
步骤 1:计算数据集 D 的经验熵 H(D)
标签 play 的分布:
yes:9 条(索引 2,3,4,6,8,9,10,11,12)no:5 条(索引 0,1,7,13,5)
经验熵公式:
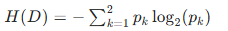
其中 pk 是标签 k 的占比。
代入计算:

步骤 2:对每个特征,计算信息增益 IG(D,A)
特征 1:outlook(取值:sunny、overcast、rainy)
-
子集划分:
sunny(D1):5 条(索引 0,1,7,8,10)→play分布:no(3 条)、yes(2 条)overcast(D2):4 条(索引 2,6,11,12)→play分布:yes(4 条)、no(0 条)rainy(D3):5 条(索引 3,4,5,9,13)→play分布:yes(3 条)、no(2 条)
-
计算各子集的经验熵:
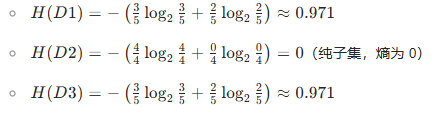
- 信息增益 IG(D,outlook):
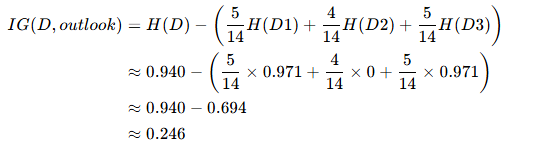
特征 2:temperature(取值:hot、mild、cool)
-
子集划分:
hot(D1):4 条(索引 0,1,2,12)→play分布:yes(2 条)、no(2 条)mild(D2):6 条(索引 3,7,9,10,11,13)→play分布:yes(4 条)、no(2 条)cool(D3):4 条(索引 4,5,6,8)→play分布:yes(3 条)、no(1 条)
-
计算各子集的经验熵:
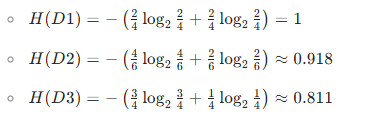
- 信息增益 IG(D,temperature):
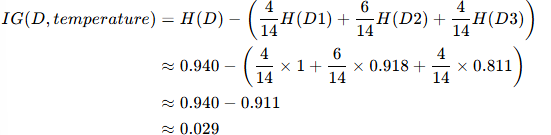
特征 3:humidity(取值:high、normal)
-
子集划分:
high(D1):7 条(索引 0,1,2,3,7,11,13)→play分布:yes(3 条)、no(4 条)normal(D2):7 条(索引 4,5,6,8,9,10,12)→play分布:yes(6 条)、no(1 条)
-
计算各子集的经验熵:
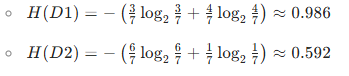
- 信息增益 IG(D,humidity):
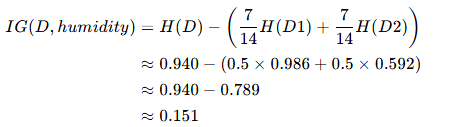
特征 4:windy(取值:FALSE、TRUE)
-
子集划分:
FALSE(D1):8 条(索引 0,2,3,4,7,8,9,12)→play分布:yes(6 条)、no(2 条)TRUE(D2):6 条(索引 1,5,6,10,11,13)→play分布:yes(3 条)、no(3 条)
-
计算各子集的经验熵:
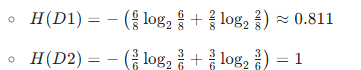
- 信息增益 IG(D,windy):
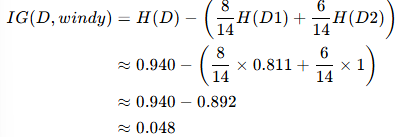
步骤 3:选择信息增益最大的特征作为根节点
对比 4 个特征的信息增益:
- IG(outlook)≈0.246(最大)
- IG(humidity)≈0.151
- IG(windy)≈0.048
- IG(temperature)≈0.029
因此,根节点选 outlook。
步骤 4:递归划分子集,构建子树
对 outlook 的每个取值(sunny、overcast、rainy),递归重复上述过程(计算子集的经验熵、信息增益,选最优特征)。
以 outlook=overcast 为例:
- 子集共 4 条样本(索引 2,6,11,12),
play全为yes→ 已是纯子集,直接生成叶节点play=yes。
以 outlook=sunny 为例:
- 子集共 5 条样本(索引 0,1,7,8,10),
play分布:no(3 条)、yes(2 条)。 - 继续计算该子集下各特征的信息增益(重复步骤 2),最终会选
humidity或其他特征进一步划分,直到所有子集都 "纯"(熵为 0)或无特征可分。
以 outlook=rainy 为例:
- 子集共 5 条样本(索引 3,4,5,9,13),
play分布:yes(3 条)、no(2 条)。 - 同样递归计算信息增益,选择最优特征(如
windy或humidity等)继续划分。
5. 最终决策树结构
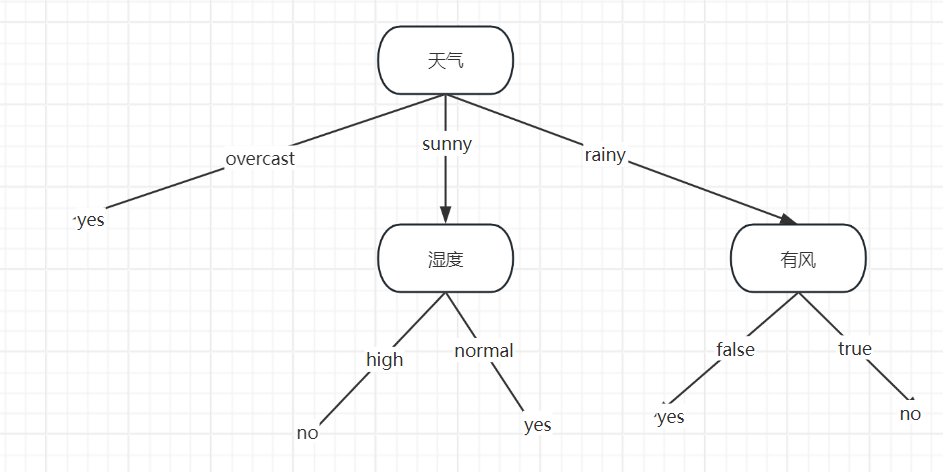
总结
ID3 算法通过 信息增益 选特征,优先拆分 "区分度最高" 的特征。对这个天气数据集,根节点是 outlook,然后递归处理各子集,直到所有叶节点 "纯"(熵为 0)。实际实现时,可通过代码(如 Python + scikit-learn 或手动递归)完整构建决策树。