下面的这个其实也是可以使用搜索的思想去进行求解,我们可以使用bfs,借助于队列进行实现的,我们也可以使用深度优先搜索,也就是递归进行实现的
1.填涂颜色问题
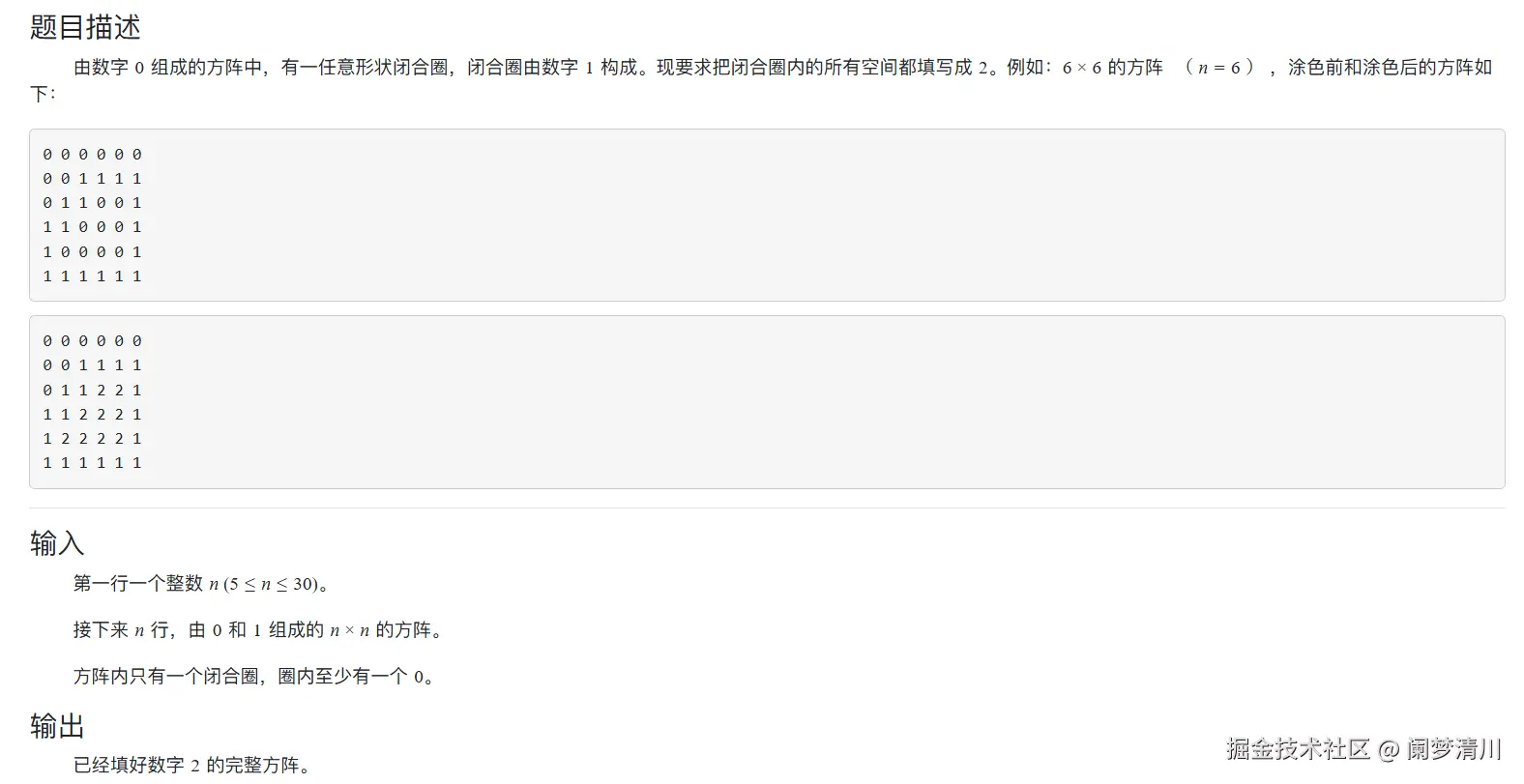
下面的这个题目其实也是非常明确的啦,主要就是需要把这些被1包裹的0修改成为2即可;
这个题目直接使用之前的bfs求解其实并不是非常的容易,这个题目其实是属于floodfill算法的相关的问题,也就是需要我们找到这个对应的联通快,修改这个具体的内容;
这个题目大部分的解法都是在外面加上一圈,刚开始我还不是非常的理解,翻了好多的资料,还是波波老师的这个视频里面的讲述是最清楚的(说到这个地方,我也是非常的感慨,就是算法这个东西,很多人都在讲,但是我觉得并不是每一个人的都适合自己,有些人和有些人直接拿还是有很大的差距的,我不否热有些讲师这个算法成绩很厉害,但是不代表这个算法的具体的原理,题目你就可以讲明白,同理,有些老师可能没有拿过这个ACM什么什么成绩,但是人家的讲解方法就是非常的不错),因此我还是洗完大家都可以找到适合自己的教程进行这个相关的学习;
为什么这个最外面需要增加一圈这个数字0,这个就是因为如果没有外圈的时候,我们需要对于每一条临街的边需要进行遍历,因为只要这个边上出现了一个1,这个时候我们就是过不去的,但是如果外面全是0,无论这个数字表格的整体的布局是设么样子的,我们都是可以直接通过起始点找到的;
总之,以上就是我看了波波老师的这个视频之后的理解,但是我觉得很少有人能够读懂,还是上面的话,我希望大家可以找到适合自己的教程,刚开始我自己学习算法的时候,也是看看这个视频讲的怎么样,看看那个视频讲的怎么样,花费了大量的时间,但是到头来这个效果却没有想象的哪个好,因此我还是建议大家在经济条件允许的这个情况下,买一份高质量的教程去学习,如果本身算法能力就很强,自学就可以,这个当然没有问题,如果你和我一样,对于别人写的代码看不懂,并且在网络上面看看这个教程,看看那个教程,为此觉得非常的浪费时间,此时,我还是非常推荐一下我正在学习的这个教程:比特算法竞赛蓝桥杯的,老师讲的真的非常地好,我敢说,这个是我自己目前遇到的全网讲解算法最详细的老师啦,当然大佬自学就可以明白,看这个也是没有问题的,我是说给那些能力一般,基础薄弱的同学的,基本上这一套课程包含了所有的蓝桥杯的算法类型,课程的资源还是非常的丰富的;
下面的这个是我们的代码:
1)这个题目里面的放下也就是上下左右的这个顺序,因此这个里面涉及到的这个方向数组里面的元素的个数就是4个;
2)主函数里面还是使用两层循环控制这个输入的过程,调用这个深度优先遍历搜索算法,然后是使用两层循环控制这个输出的过程,如果这个元素不是0,我们直接输出,如果st表示的是true,证明这个就是边缘的元素,我们直接输出这个0 即可,否则没有被标记,就说明这个事被包裹着的0,我们需要全部输出2几个
3)但是这个输出的过程我们还是需要注意以下的,因为这个外围的0我们是不需要进行这个输出的,因此这个输出时候的两个循环都是从这个1开始的,这个表示的就是把外围的过滤掉了;
4)还有就是这个里面的空格的问题,也是我是用的这个网站的自己的问题,因此控制一下,如果有些网站的检查如果不是非常的严格的话,这个题目应该就是可以通过的;
5)主要还是这个标记数组,这个if(a[i][j处理的就是1的情况,剩下的else都是0的情况,然后这个0的情况也被划分为这个打标记的0和没有打标记的0,这个处理输出的内容都是不一样的;
ini
#include <iostream>
#include <cstring>
using namespace std;
const int N = 35;
int n;
int a[N][N];
bool st[N][N]; // 只会标记边缘的 0
int dx[] = {0, 0, -1, 1};
int dy[] = {1, -1, 0, 0};
void dfs(int i, int j)
{
st[i][j] = true;
for(int k = 0; k < 4; k++)
{
int x = i + dx[k], y = j + dy[k];
// 注意此时的边界
if(x >= 0 && x <= n + 1 && y >= 0 && y <= n + 1 && a[x][y] == 0 && st[x][y] == 0)
{
dfs(x, y);
}
}
}
int main()
{
while(cin >> n)
{
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
cin >> a[i][j];
dfs(0, 0);
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= n; j++)
{
if(j!=1) cout<<" ";
if(a[i][j]) cout << a[i][j];
else if(st[i][j]) cout << 0;
else cout << 2 ;
}
cout << endl;
}
}
return 0;
}