算法——BFS

目录

[BFS解决 FloodFill 算法](#BFS解决 FloodFill 算法)

图像渲染

岛屿数量

岛屿的最大面积

被围绕的区域

BFS解决最短路径问题

迷宫中离入口最近的出口

最小基因变化

单词接龙​编辑

为高尔夫比赛砍树

多源BFS

[01 矩阵](#01 矩阵)

飞地的数量

地图中的最高点

地图分析

BFS解决拓扑排序

课程表

[课程表 II](#课程表 II)

火星词典

---

BFS解决 FloodFill 算法

FloodFill 算法主要用于解决在一个区域中，寻找性质相同的联通块。

图像渲染

**思路：**借助队列，从题目给出的源点进行宽搜，先将源点入队列，之后每次从队列取出一个元素，将这个元素表示的位置颜色进行修改（即改数组值），修改后遍历这个元素上下左右四个位置，如果有符合条件的节点就加入队列中，以此类推，直到队列为空。

代码：

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
public:
    vector<vector<int>> floodFill(vector<vector<int>>& image, int sr, int sc, int color) {
        int prev = image[sr][sc]; //把修改前的值记录下来
        if(prev == color) //如果修改前的值和要修改的值一样，就没有必要修改了
            return image;

        int m = image.size();
        int n = image[0].size(); //后面判断越界用
        queue<pair<int, int>> q;
        q.push({sr, sc});
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            image[p.first][p.second] = color; 
            for(int i = 0; i < 4; i++){
                int x = p.first + dx[i];
                int y = p.second + dy[i];
                if(x >= 0 && x < m && y >= 0 && y < n && image[x][y] == prev){ //判断越界和是否需要入队列
                    q.push({x, y});
                }
            }
        }

        return image;
    }
};

岛屿数量

**思路：**首先定义一个数组（命名为 visited），用来标记哪些 1 被遍历过了，遍历二维矩阵，遇到没有被统计过的 1，就通过 BFS 的方式找到这个 1 所在的整个岛屿，并且将这个岛屿中所有的 1 都在 visited 中标记一次，然后岛屿数量加 1，这样后续遍历遇到的 1 如果还是这个岛屿中的，因为有 visited 的缘故，就不会造成重复统计的问题了。

**BFS 找整个岛屿：**还是使用队列，先将遇到的第一个 1 的坐标入队列，然后当队列不为空时，依次取出队列元素，在标记数组中对这个坐标进行标记，对这个坐标上下左右位置进行判断，如果是1 就继续入队列，直到队列为空且没有元素入队列，此时这个岛屿标记完毕。

**细节：**每个节点入队列的时候就要在 visited 中标记，如果出队列的时候再标记，有的节点会重复入队列。

代码：

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    int visited[301][301];
    int m;
    int n;
public:
    int numIslands(vector<vector<char>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int ret = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == '1' && visited[i][j] == false){
                    ret++;
                    bfs(grid, i, j);
                }
            }
        }

        return ret;
    }

    void bfs(vector<vector<char>>& grid, int i, int j){
        queue<pair<int, int>> q;
        q.push({i, j});
        visited[i][j] = true;
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            for(int k = 0; k < 4; k++){
                int x = p.first + dx[k];
                int y = p.second + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == '1' && visited[x][y] == false){
                    q.push({x, y});
                    visited[x][y] = true; //加入队列时就要标记，否则有的节点会重复入队列
                }
            }
        }
    }
};

岛屿的最大面积

**思路：**遍历二维矩阵，当遇到一个没有统计过的 1 时，使用 BFS 统计出这个 1 所在整个岛屿的 1 的数量，这个 1 的个数就是面积，然后取所有面积中最大的即可。BFS遍历岛屿还是借助队列，先将第一个遇到的 1 丢入队列，然后当队列不为空时，依次取出队列元素，然后判断取出元素的上下左右是否存在没有统计的 1，有就让它入队列，直到队列为空，这个岛屿就统计完成，找出整个岛屿的同时记录岛屿的面积（即 1 的数量）。标记 1 是否统计过使用一个标记数组即可。

代码：

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool visited[51][51];
    int m;
    int n;
public:
    int maxAreaOfIsland(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        int ret = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1 && visited[i][j] == false){
                    ret = max(ret, bfs(grid, i, j));
                }
            }
        }

        return ret;
    }

    int bfs(vector<vector<int>>& grid, int i, int j){
        int count = 1; //记录 1 的个数
        queue<pair<int, int>> q;
        q.push({i, j});
        visited[i][j] = true;
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            for(int k = 0; k < 4; k++){
                int x = p.first + dx[k];
                int y = p.second + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && visited[x][y] == false){
                    q.push({x, y});
                    count++;
                    visited[x][y] = true;
                }
            }
        }

        return count;
    }
};

被围绕的区域

**思路：**正难则反，这道题如果直接找被包围的并修改比较困难，我们可以先遍历矩阵的四个边，找没有被包围的部分，然后把没有为包围的 'O' 标记一下，然后遍历二维矩阵，当遇到没有被标记的 'O'，说明它是被包围的，使用 BFS 找到整块区域，并且边找边修改。

代码：

class Solution {
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool visited[201][201];
    int m;
    int n;
public:
    void solve(vector<vector<char>>& board) {
        m = board.size();
        n = board[0].size();
        
        //遍历第一行和最后一行
        for(int i = 0; i < n; i++){
            if(board[0][i] == 'O' && visited[0][i] == false){
                bfs(board, 0, i, false);
            }
            if(board[m - 1][i] == 'O' && visited[m - 1][i] == false){
                bfs(board, m - 1, i, false);
            }
        }
        //遍历第一列，最后一列
        for(int i = 0; i < m; i++){
            if(board[i][0] == 'O' && visited[i][0] == false){
                bfs(board, i, 0, false);
            }
            if(board[i][n - 1] == 'O' && visited[i][n - 1] == false){
                bfs(board, i, n - 1, false);
            }
        }

        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(board[i][j] == 'O' && visited[i][j] == false){
                    bfs(board, i, j, true);
                }
            }
        }
    }

    void bfs(vector<vector<char>>& board, int i, int j, bool isChange){
        queue<pair<int, int>> q;
        q.push({i, j});
        visited[i][j] = true;
        if(isChange){
            board[i][j] = 'X';
        }
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            for(int k = 0; k < 4; k++){
                int x = p.first + dx[k];
                int y = p.second + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && board[x][y] == 'O' && visited[x][y] == false){
                    q.push({x, y});
                    visited[x][y] = true;
                    if(isChange){
                        board[x][y] = 'X';
                    }
                }
            }
        }
    }
};

BFS解决最短路径问题

BFS 可以解决边权相同的最短路径问题，先将源点入队列（这是宽搜拓展的第一层），然后弹出源点时将和源点相关的点全部入队列（此时相当于宽搜向外拓展了一层），然后这些点一起弹出，同样，弹出时和这些点相关的点进入队列（又拓展一层），依次类推，直到目标点进入队列，BFS 过程结束，拓展的层数就是最短的路径长度。

迷宫中离入口最近的出口

**思路：**这道题本质其实就是一个边权相同的最短路径问题，通过 BFS 从源点不断向外拓展（层序遍历），每拓展一层就是走了一步，拓展过程中遇到矩阵的边（不是墙的边）说明到出口了，拓展结束，直接返回结果，如果整个层序遍历结束，还没有返回结果，说明没有出口，返回 -1。

代码：

class Solution {
public:
    int nearestExit(vector<vector<char>>& maze, vector<int>& entrance) {
        int  m = maze.size();
        int n = maze[0].size();
        vector<vector<bool>> visited(m, vector<bool>(n, false)); //标记当前位置是否已经走过了
        int dx[4] = {0, 0, 1, -1};
        int dy[4] = {1, -1, 0, 0};
        int ret = 0; //记录步数
        queue<pair<int, int>> q;
        q.push({entrance[0], entrance[1]});
        visited[entrance[0]][entrance[1]] = true;
        while(!q.empty()){
            ret++;
            int sz = q.size();
            for(int i = 0; i < sz; i++){
                pair<int, int> p = q.front();
                q.pop();
                for(int k = 0; k < 4; k++){
                    int x = p.first + dx[k];
                    int y = p.second + dy[k];
                    if(x >= 0 && x < m && y >= 0 && y < n && maze[x][y] == '.' && visited[x][y] == false){
                        if(x == 0 || x == m - 1 || y == 0 || y == n - 1){
                            return ret;
                        }
                        q.push({x, y});
                        visited[x][y] = true;
                    }
                }
            }
        }

        return -1; //没有出口
    }
};

最小基因变化

**思路：**这道题的本质还是一个边权相同的最短路径问题，起始字符串可以进行若干次合理的变化，然后找变化次数最少且和 end 字符串一样。如图：

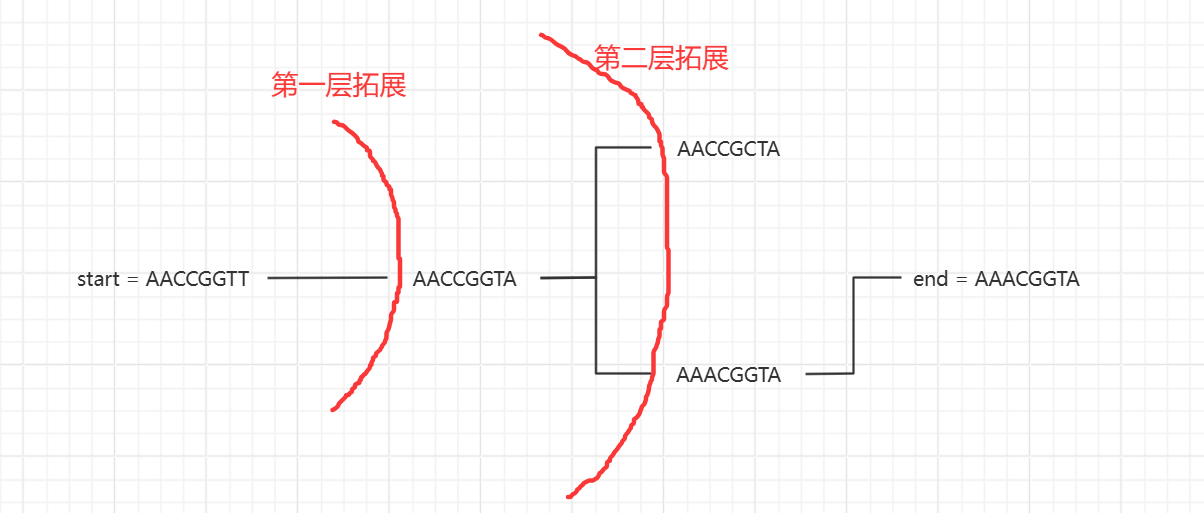
对上图这种情况进行一次 BFS 即可，字符的合理的变化可以通过两层循环解决，第一层循环遍历字符串的八个字母，对这八个字母依次修改，第二层循环遍历四次，作用是对当前字母修改四次，因为每个字母都可以是 A，C，G，T中的任何一个，这样就能枚举只变化一个字符的所有情况，然后每修改一个字母后就判断一下当前字符串是否合理，合理且和 end 相同就直接返回结果，合理且和 end 不相同就将这个字符串丢入队列继续下一轮变化。

BFS 拓展的层数就是变化的次数，while（q.size()）这个循环每进行一次，是拓展了一层，虽然这一次循环可能向队列放入了多个元素，但是这些元素相比如上一轮循环的字符串都只变化了一个字母，所以只是向外拓展了一层。

代码：

class Solution 
{
public:
    int minMutation(string startGene, string endGene, vector<string>& bank) 
    {
        unordered_set<string> vis;
        unordered_set<string> hash(bank.begin(), bank.end());
        string change = "ACGT";

        if(startGene == endGene)
            return 0;

        if(!hash.count(endGene))
            return -1;

        queue<string> q;
        q.push(startGene);
        vis.insert(startGene);
        int ret = 0;
        while(q.size())
        {
            ret++;
            int sz = q.size();
            while(sz--)
            {
                string t = q.front();
                q.pop();
                for(int i = 0; i < 8; i++)
                {
                    string tmp = t;
                    for(int j = 0; j < 4; j++)
                    {
                        tmp[i] = change[j];
                        if(hash.count(tmp) && !vis.count(tmp))
                        {
                            if(tmp == endGene)
                                return ret;

                            q.push(tmp);
                            vis.insert(tmp);
                        }
                    }
                }
            }
        }

        return -1;
    }
};

单词接龙

**思路：**这道题思路和最小基因序列那道题思路一样（就是上一道题），这里不赘述了。

代码：

class Solution 
{
public:
    int ladderLength(string beginWord, string endWord, vector<string>& wordList) 
    {
        unordered_set<string> check;
        unordered_set<string> hash(wordList.begin(), wordList.end());

        if(!hash.count(endWord))
            return 0;

        int ret = 1;
        queue<string> q;
        q.push(beginWord);
        check.insert(beginWord);
        while(q.size())
        {
            ret++;
            int sz = q.size();
            for(int i = 0; i < sz; i++)
            {
                string t = q.front();
                q.pop();
                for(int j = 0; j < beginWord.size(); j++)
                {
                    string tmp = t;
                    for(int k = 0; k < 26; k++)
                    {
                        tmp[j] = 'a' + k;
                        if(hash.count(tmp) && !check.count(tmp))
                        {
                            if(tmp == endWord)
                                return ret;
                            q.push(tmp);
                            check.insert(tmp);
                        }
                    }
                }
            }
        }

        return 0;
    }
};

为高尔夫比赛砍树

**思路：**如例1，我们需要从 1 开始，按照 2->3->4->5->6->7 的顺序依次砍树，我们可以把它看成若干次迷宫问题，第一次是1 是入口，2 是出口，找 1->2 的最短路径，第二次 2 是入口，3 是出口，找 2->3的最短路径。但是在解决迷宫问题之前，我们需要先确定这些数的坐标的顺序，使用一个容器，根据数从小到大的排列（这些数的大小关系不用存储，存储的是坐标），将对应的坐标的顺序也存储出来。

代码：

class Solution 
{
    int m, n;
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
    bool check[51][51];
public:
    int cutOffTree(vector<vector<int>>& forest) 
    {
        m = forest.size();
        n = forest[0].size();
        vector<pair<int, int>> v;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(forest[i][j] > 1)
                    v.push_back({i, j});
            }
        }
        sort(v.begin(), v.end(), [&](const pair<int, int>& p1, const pair<int, int>& p2){
            return forest[p1.first][p1.second] < forest[p2.first][p2.second];
        });


        int bx = 0, by = 0;
        int ret = 0;
        for(int i = 0; i < v.size(); i++)
        {
            int step = bfs(forest, bx, by, v[i].first, v[i].second);
            if(step == -1)
                return -1;

            ret += step;
            bx = v[i].first;
            by = v[i].second;
        }

        return ret;
     }

    int bfs(vector<vector<int>>& f, int bx, int by, int ex, int ey)
    {
        if(bx == ex && by == ey)
            return 0;

        memset(check, 0, sizeof(check));
        queue<pair<int, int>> q;
        q.push({bx, by});
        check[bx][by] = true;
        int step = 0;
        while(q.size())
        {
            step++;
            int sz = q.size();
            while(sz--)
            {
                auto [a, b] = q.front();
                q.pop();
                for(int k = 0; k < 4; k++)
                {
                    int x = a + dx[k];
                    int y = b + dy[k];
                    if(x >= 0 && x < m && y >= 0 && y < n && f[x][y] && !check[x][y])
                    {
                        if(x == ex && y == ey)
                            return step;

                        q.push({x, y});
                        check[x][y] = true;
                    }
                }
            }
        }

        return -1;
    }
};

多源BFS

01 矩阵

**思路：**把所有的 0 当成一个起点，1 当成终点，开始时直接把所有的 0 位置加入队列，这样就能把所有 0 当做一个起点，然后像单源最短路问题那样一层一层向外扩展即可。这里存放结果的二维矩阵所有位置的值都初始化成 -1，这样就不用 visited 数组来标记哪里没有走过了，因为如果当前位置的值是 -1，就是没有走过的，如果不是，就表明当前位置已经被遍历过了，另外，这道题因为要更新距离，通常使用 step 记录走的步数（即拓展的层数），但是这里也不需要 step，只需要使用拓展到当前点的那个点的值加 1 就行，因为每次拓展一层，距离只会在上一层的基础之上加 1。

代码：

class Solution {
public:
    vector<vector<int>> updateMatrix(vector<vector<int>>& mat) {
        int m = mat.size();
        int n = mat[0].size();
        int dx[4] = {0, 0, 1, -1};
        int dy[4] = {1, -1, 0, 0};
        vector<vector<int>> ret(m, vector<int>(n, -1));
        queue<pair<int, int>> q;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(mat[i][j] == 0){
                    q.push({i, j});
                    ret[i][j] = 0;
                }
            }
        }

        while(!q.empty()){
            int sz = q.size();
            for(int i = 0; i < sz; i++){
                pair<int, int> p = q.front();
                q.pop();
                for(int k = 0; k < 4; k++){
                    int x = p.first + dx[k];
                    int y = p.second + dy[k];
                    if(x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1){
                        q.push({x, y});
                        ret[x][y] = ret[p.first][p.second] + 1;
                    }
                }
            }
        }

        return ret;
    }
};

飞地的数量

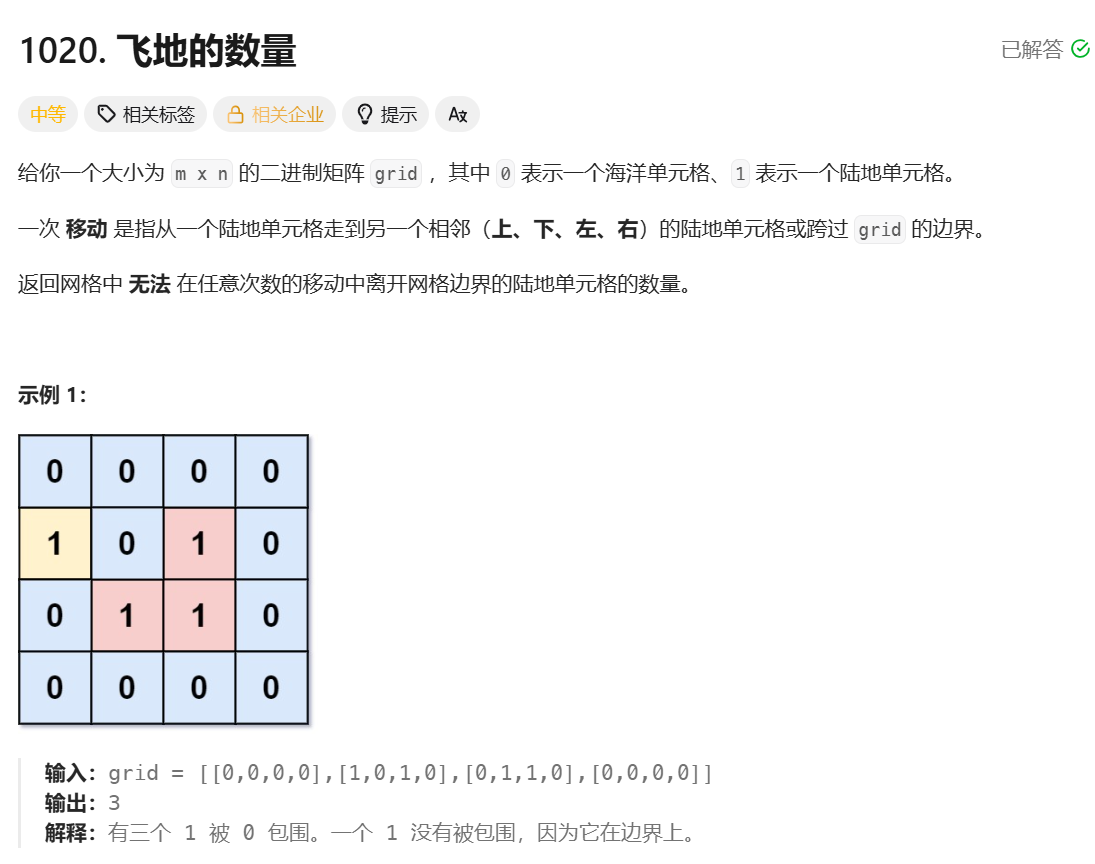
**思路：**遍历二维矩阵的四个边，将所有的 1 丢入队列中作为一个起点，然后进行一次 bfs，将和边界相连的所有 1 全部找到并且标记，然后再遍历一次二维矩阵，统计所有没被标记的 1 即可。

代码：

class Solution {
public:
    int numEnclaves(vector<vector<int>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        queue<pair<int, int>> q;
        vector<vector<bool>> visited(m, vector<bool>(n, false));
        //将所有的 1 丢入队列，并且标记
        for(int i = 0; i < m; i++){
            if(grid[i][0] == 1){
                q.push({i, 0});
                visited[i][0] = true;
            }
            if(grid[i][n - 1] == 1){
                q.push({i, n - 1});
                visited[i][n - 1] = true;
            }
        }
        for(int i = 0; i < n; i++){
            if(grid[0][i] == 1){
                q.push({0, i});
                visited[0][i] = true;
            }
            if(grid[m - 1][i] == 1){
                q.push({m - 1, i});
                visited[m - 1][i] = true;
            }
        }

        //bfs找所有和边缘的1相连的1，并标记
        int dx[4] = {0, 0, 1, -1};
        int dy[4] = {1, -1, 0, 0};
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            for(int k = 0; k < 4; k++){
                int x = p.first + dx[k];
                int y = p.second + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && grid[x][y] == 1 && visited[x][y] == false){
                    q.push({x, y});
                    visited[x][y] = true;
                }
            }
        }

        int ret = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1 && visited[i][j] == false){
                    ret++;
                }
            }
        }

        return ret;
    }
};

地图中的最高点

**思路：**创建一个存储结果的矩阵，因为水域的高度必须是 0，陆地的高度要取决于它旁边格子的高度，所以我们可以先遍历题目给出的二维矩阵，然后在结果矩阵中将所有是水域的地方标记为 0，并且放到一个队列中，然后通过 bfs 的方式从 0 开始向外一层一层拓展，每拓展一层，高度就加 1。相当于把所有水域的节点看做成一个源点，然后向外搜索。每个节点的高度是拓展到当前点的那个点的值加 1 就行，因为每次拓展一层，距离只会在上一层的基础之上加 1。

代码：

class Solution {
public:
    vector<vector<int>> highestPeak(vector<vector<int>>& isWater) {
        int m = isWater.size();
        int n = isWater[0].size();
        queue<pair<int, int>> q;
        vector<vector<int>> ret(m, vector<int>(n, -1));
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(isWater[i][j] == 1){
                    ret[i][j] = 0;
                    q.push({i, j});
                }
            }
        }

        int dx[4] = {0, 0, 1, -1};
        int dy[4] = {1, -1, 0, 0};
        while(!q.empty()){
            pair<int, int> p = q.front();
            q.pop();
            for(int k = 0; k < 4; k++){
                int x = p.first + dx[k];
                int y = p.second + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1){
                    ret[x][y] = ret[p.first][p.second] + 1;
                    q.push({x, y});
                }
            }
        }

        return ret;
    }
};

地图分析

**思路：**创建一个和题目给出的数组同等规模的数组（命名为 ret），ret 中所有值都初始化成 -1，根据题目描述，我们可以认为陆地（即题目数组中 1 的位置）高度为 0 ，和它直接相连的海洋高度为 1，然后每向外拓展一层海洋，这层海洋的高度就在原有的基础上加 1，这个高度正好是和曼哈顿距离相等的，这样我们就只需要遍历题目给出的数组，当遇到值为 1 的节点，就在 ret 数组中将相同位置的值标记为 0，表明高度是 0，并且将这些节点丢入队列中，遍历结束，所有陆地节点都在队列中，将这些节点看成一个源点，通过 bfs 向外拓展，边拓展边标记高度，最后最高的高度就是最大的曼哈顿距离。

代码：

class Solution 
{
    int dx[4] = {0, 0, 1, -1};
    int dy[4] = {1, -1, 0, 0};
public:
    int maxDistance(vector<vector<int>>& grid) 
    {
        int m = grid.size();
        int n = grid[0].size();
        vector<vector<int>> ret(m, vector<int>(n, -1));

        queue<pair<int, int>> q;
        for(int i = 0; i < m; i++)
        {
            for(int j = 0; j < n; j++)
            {
                if(grid[i][j] == 1)
                {
                    ret[i][j] = 0;
                    q.push({i, j});
                }
            }
        }

        int result = -1;
        while(q.size())
        {
            auto [a, b] = q.front();
            q.pop();
            for(int k = 0; k < 4; k++)
            {
                int x = a + dx[k];
                int y = b + dy[k];
                if(x >= 0 && x < m && y >= 0 && y < n && ret[x][y] == -1)
                {
                    ret[x][y] = ret[a][b] + 1;
                    result = max(result, ret[x][y]);
                    q.push({x, y});
                }
            }
        }

        return result;
    }
};

BFS解决拓扑排序

拓扑排序

• 概念：在AOV网（顶点活动图，即一个有向图，其中顶点表示活动，边表示这些活动的先后顺序）中找到做事情的先后顺序，拓扑排序的结果可能不是唯一的。
• 步骤：
  • 找到图中入度为 0 的点，取出来。
  • 删除与这个点连接的边。
  • 重复上面两步操作，直到图中没有点或者没有入度为 0 的点。

**实现拓扑排序：**借助队列，来一次 BFS 即可。

1. 初始化：把所有入度为 0 的点加入到队列中
2. 当队列不为空的时候
   1. 拿出队头元素，加入最终结果中；
   2. 删除与该元素相连的边；
   3. 判断：与删除边相连的点，是否入度变成 0，如果入度为 0，加入到队列中。

课程表

**思路：**这道题中课程和课程的先后顺序构成了一个有向图，判断是否可能完成所有课程的学习其实就是判断有向图是否有环。先建图，并且将每个点的入度存储起来，然后借助队列进行 bfs，取出队头元素，将这个点指向的其他点的入度减 1，判断这个点入度是否为 0，如果为 0，将其加入队列。当队列为空时，判断是否还有点的入度不为 0，如果有，就说明成环了，不可能完成所有课程的学习。

代码：

class Solution {
public:
    bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
        unordered_map<int, vector<int>> hash; //建立邻接表
        vector<int> in(numCourses);  //存储每个节点的入度

        //建图，存储入度
        for(auto& v : prerequisites){
            int a = v[0];
            int b = v[1];
            hash[b].push_back(a);
            in[a]++;
        }

        //bfs 将所有入度为 0 的节点入队列
        queue<int> q;
        for(int i = 0; i < numCourses; i++){
            if(in[i] == 0){
                q.push(i);
            }
        }

        while(!q.empty()){
            int f = q.front();
            q.pop();
            for(auto& v : hash[f]){
                in[v]--;
                if(in[v] == 0){
                    q.push(v);
                }
            }
        }

        for(int i = 0; i < numCourses; i++){
            if(in[i] != 0){
                return false;
            }
        }

        return true;
    }
};

课程表 II

**思路：**这道题思路和上一道题一样，只不过上一道题判断是否成环，这道题是把拓扑排序后的结果返回。

代码：

class Solution 
{
public:
    vector<int> findOrder(int n, vector<vector<int>>& prerequisites) 
    {
        unordered_map<int, vector<int>> edges;
        vector<int> in(n);
        vector<int> ret;

        for(auto e : prerequisites)
        {
            int a = e[0];
            int b = e[1];
            edges[b].push_back(a);
            in[a]++;
        }

        queue<int> q;
        for(int i = 0; i < n; i++)
        {
            if(in[i] == 0)
                q.push(i);
        }

        while(q.size())
        {
            int f = q.front();
            q.pop();
            ret.push_back(f);
            for(auto e : edges[f])
            {
                in[e]--;

                if(in[e] == 0)
                    q.push(e);
            }
        }

        for(int i = 0; i < n; i++)
        {
            if(in[i] != 0)
                return vector<int>();
        }
        return ret;
    }
};

火星词典

**思路：**遍历字符串，将字符之间的先后顺序转化成有向图，然后通过这个有向图进行拓扑排序，如果能排出来，没有成环，就直接返回结果，如果有环就返回空字符串就行。详细过程看代码。

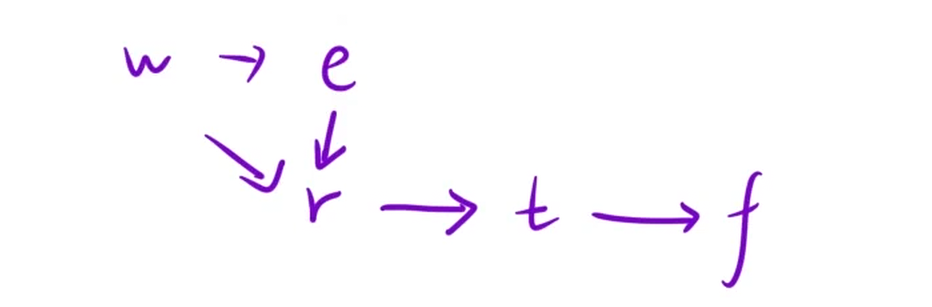
代码：

class Solution 
{
    unordered_map<char, unordered_set<char>> edges;//邻接表存储图
    unordered_map<char, int> in; //统计入度
    bool check;//处理特殊情况（如：abc ab）
public:
    string alienOrder(vector<string>& words) 
    {
        //初始化入度
        for(auto& s : words)
        {
            for(auto ch : s)
            {
                in[ch] = 0;
            }
        }
        //建图
        int n = words.size();
        for(int i = 0; i < n; i++)
        {
            for(int j = i + 1; j < n; j++)
            {
                add(words[i], words[j]);
                if(check)
                    return "";
            }
        }

        //拓扑排序
        queue<char> q;
        for(auto& [a, b] : in)
        {
            if(b == 0)
                q.push(a);
        }

        string ret;
        while(q.size())
        {
            char t = q.front();
            q.pop();
            ret += t;
            for(char ch : edges[t])
            {
                if(--in[ch] == 0)
                    q.push(ch);
            }
        }

        //判断是否合法
        for(auto& [a, b] : in)
        {
            if(b != 0)
                return "";
        }
        return ret;
    }

    void add(string& s1, string& s2)
    {
        int n = min(s1.size(), s2.size());
        int i = 0;
        for(; i < n; i++)
        {
            if(s1[i] != s2[i])
            {
                char a = s1[i];
                char b = s2[i];
                if(!edges.count(a) || !edges[a].count(b))
                {
                    edges[a].insert(b);
                    in[b]++;
                }
                break;
            }
        }

        if(i == s2.size() && i < s1.size())
            check = true;
    }
};