1.关于二叉树构建的题目
下面的这个就是关于这个二叉树构建的题目的具体的内容;
其实这个题目并不是非常的难以理解,当时我们在学习这个数据结构与算法这个课程的时候,是一定遇到过这个类似的问题的,因为这个二叉树的还原的问题还是非常的经典的;
比如给你一个前序遍历和中序遍历,这个时候让你推理出来这个二叉树是什么样子的,下面的这个题目是告诉你了这个中序遍历和后序遍历的结果,需要求解出来这个二叉树的具体的结构
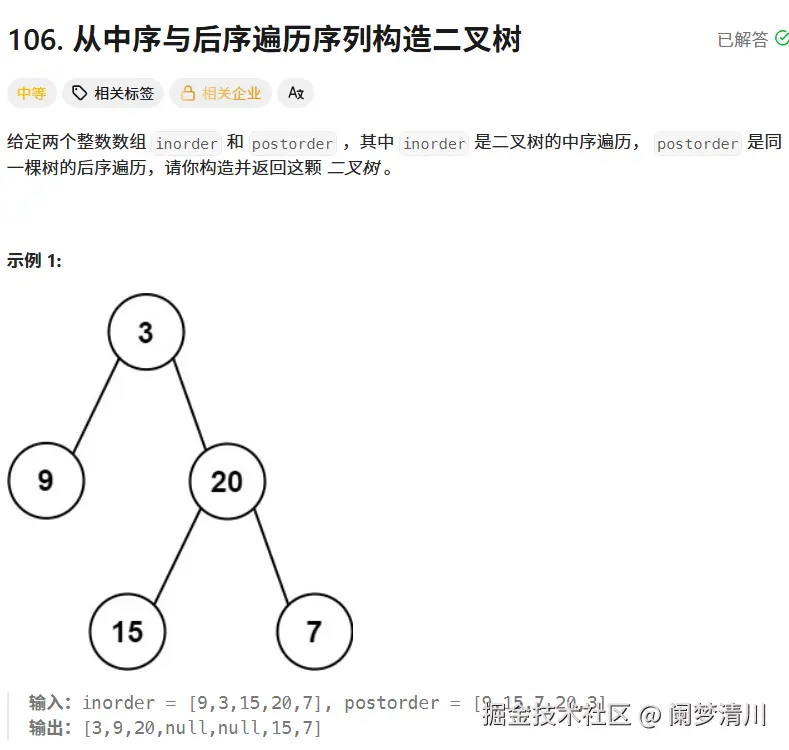
上面的这个案例里面就出来的inorder表示的就是中序遍历的结果,这个postorder数组里面的内容就是我们的二叉树后序遍历的结果,根据这两个结果我们是可以把这个二叉树构建出来的,并且把这个前序遍历的结果输出出来即可,在这个输出的过程当中,我们的没有节点的地方使用null代替输出即可;
下面的这个是题目对应的解析:因为这个题目给定的条件就是中序遍历和后序遍历,我们需要知道这个中序遍历和后序遍历区别,又因为这个后序遍历的最后一个就是根节点,因此我们的这个后序遍历的最后一个节点,就是我们根节点,根据这个后序遍历里面找到的这个根节点,我们就可以在这个中序遍历里面去应用;
因此这种题目正确的流程应该是下面的这个样子的:
1)根据这个后序遍历的结果的最后一个数字找到这个根节点
2)查看这个根节点在我们的中序遍历里面的位置,这个时候可以判断出来这个左子树和右子树
3)接着上面的过程,找到倒数第二个元素,作为新的根节点,继续去分割中序遍历里面的左子树和右子树

下面的这个就是根据中序遍历和后序遍历进行二叉树构建的代码:
1)这个里面主要的逻辑是buildtree这个函数,上面的helper函数是辅助函数,也就是我们的自定义函数;
2)通过size()-1找到这个最后一个元素,把这个下标记录下来;
3)因为我们可以在这个后序遍历里面快速的定位到这个根节点,就是最后一个元素,但是中序遍历不好找,因此这个代码里面我们使用哈希表进行记录,方便我们后续查找这个根节点在我们的中序里面的下标;
4)helper函数第一行是这个函数的结束条件;
5)首先使用哈希表快速的找到这个中序遍历里面的根节点,定义为index,每一次取出来这个后序遍历里面的最后一个元素之后,postindex--,继续从我们的新的后序遍历集合里面找到最后一个,这个helper函数的最后两行就是进行这个新一轮的查找过程,也就是构建二叉树的过程,相当于是在中序的基础上拆分成为两个新的字数,继续上述的这个过程;
ini
class Solution {
int post_index;
unordered_map<int,int> index_map;
public:
TreeNode* helper(int in_left,int in_right,vector<int>& inorder,vector<int>& postorder)
{
if(in_left>in_right) return nullptr;
int root_val=postorder[post_index];
TreeNode* root=new TreeNode(root_val);
int index=index_map[root_val];
post_index--;
root->right=helper(index+1,in_right,inorder,postorder);
root->left=helper(in_left,index-1,inorder,postorder);
return root;
}
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
post_index=(int)postorder.size()-1;
int index=0;
for(auto& val:inorder){
index_map[val]=index++;
}
return helper(0,(int)inorder.size()-1,inorder,postorder);
}
};