控制建模matlab练习11：伯德图

此练习主要是：关于伯德图
①什么是伯德图；
②伯德图的叠加性；

一、什么是伯德图：

上部分，是输出的振幅响应 随输入频率的变化；（幅频图）

下部分，是输出的相位响应 随输入频率的变化；（相频图）

二、在MATLAB中画伯德图

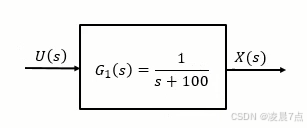
像上图这样知道传递函数的系统；
画伯德图的时候，可以一行命令直接画出；

matlab 复制代码

clc;clear;close all;
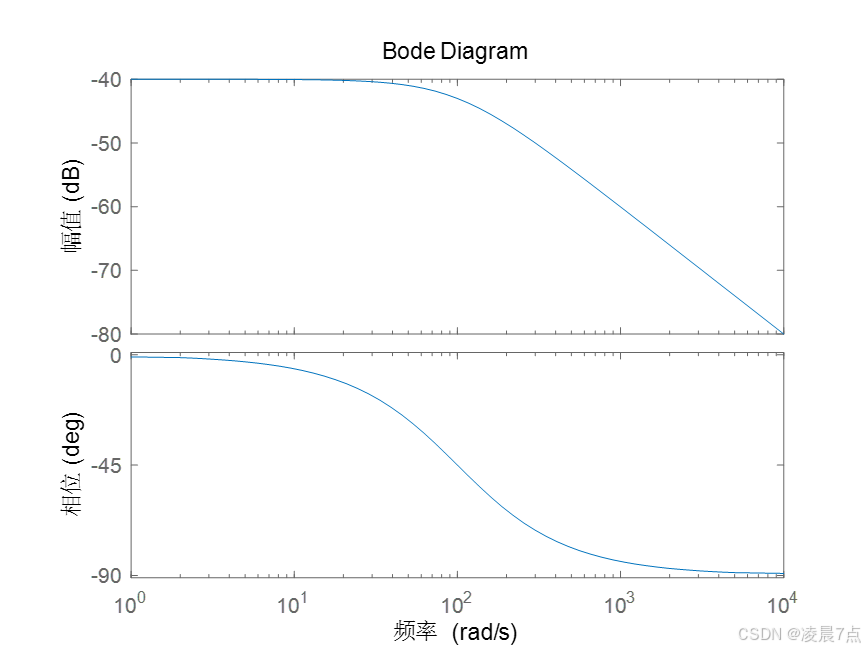
bode(tf([1],[1 100]));

运行结果：

可以看出，这是一个低通滤波器，截止频率就是100rad/s；

三、伯德图的叠加性

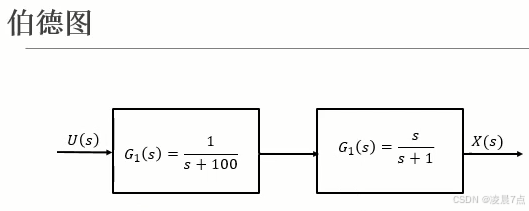
当如下图，两个传递函数串联在一起时；
整个系统的伯德图，就是两个传递函数的伯德图的叠加；

matlab 复制代码

clc;clear;close all;
%% 定义G(s)
G1_s = tf([1],[1 100]);
G2_s = tf ([1 0],[1 1]);
G3_s = G1_s * G2_s; % 两个传递函数串联，相乘
%% 绘图
figure (1) 
bode(G1_s);
title('G1(s)伯德图');
figure (2) 
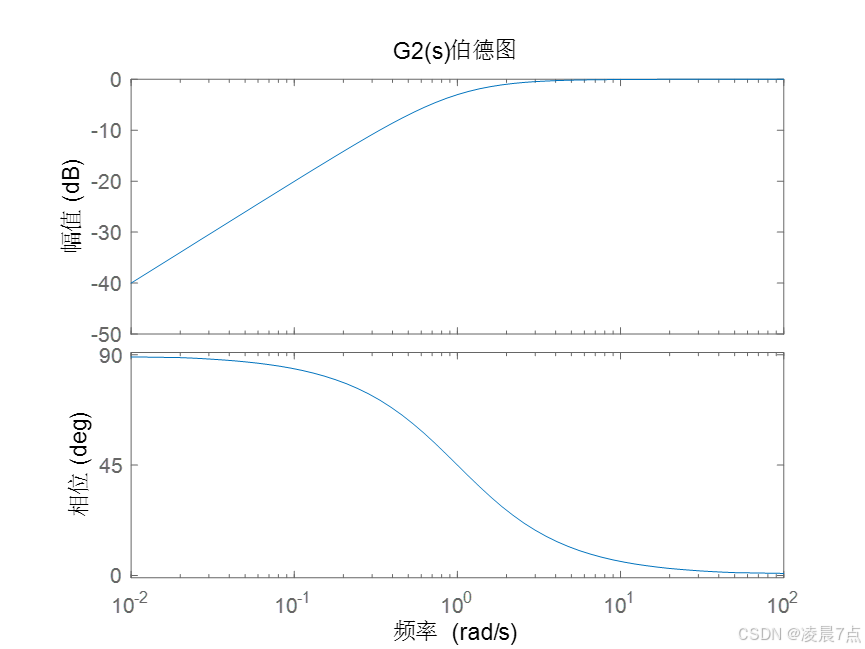
bode(G2_s);
title('G2(s)伯德图');
figure (3)
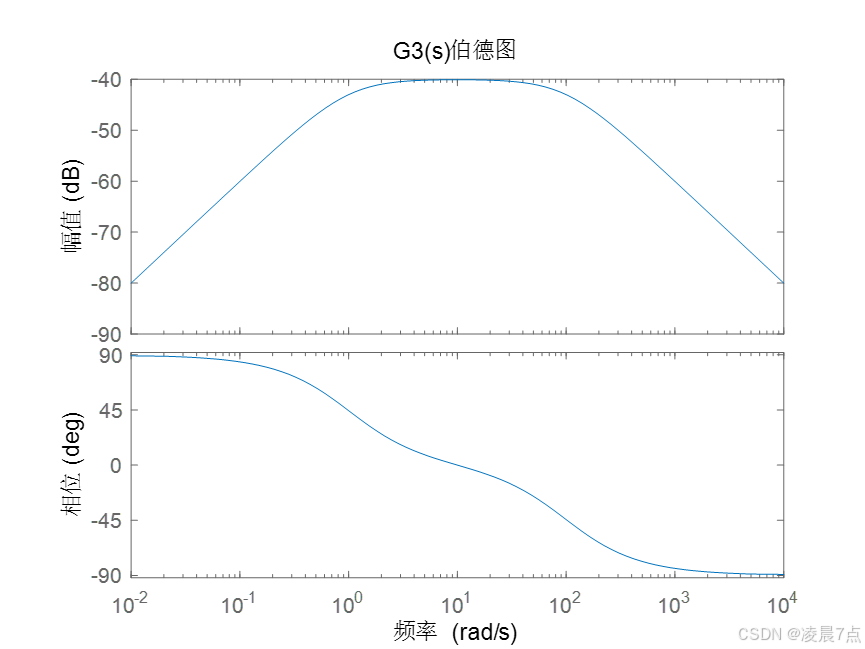
bode(G3_s);
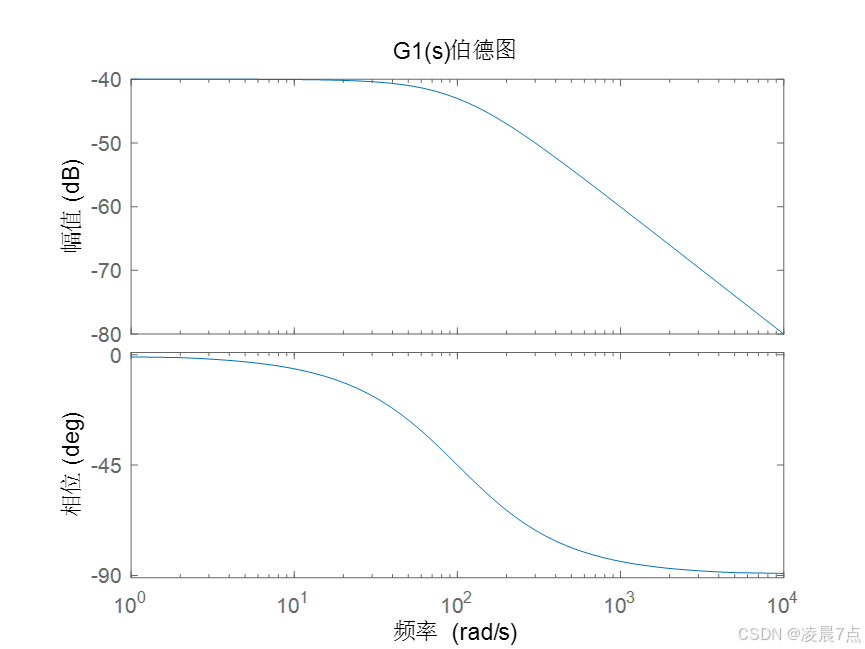
title('G3(s)伯德图');

运行结果：

G1_s是低通滤波器 ，截止频率是100rad/s ；
G2_s是高通滤波器 （因为分子部分有一个零点是0），截止频率是1rad/s；
G3_s是带通滤波器 ，只有频率在1rad/s和100rad/s之间，信号才会被大部分保留；

四、伯德图的应用

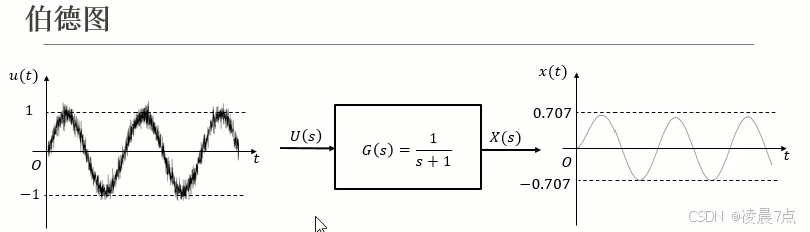
伯德图的一个应用：使用传递函数进行滤波。
例如：下图，含有很多噪音的正弦函数，输入到图中的低通滤波器当中，即可滤掉噪音。（因为噪音是高频的）

matlab 复制代码

clc;clear;close all;
%% 定义G(s)
G_s = tf([1],[1 1]);
%% 定义正弦输入 + 噪音
t = 0 : 0.01 : 20;
u = sin(t);
u =  u + 0.2*rand(size(t));
% rand(size(t)，从0到1之间，和t有同样长度的随机数列。
% 乘上0.2模拟噪音，因为这个噪音每0.01s就有一个数据，所以频率是比较高的。
subplot (2,1,1);
plot (t,u);
grid on;
%% 通过滤波器
y = lsim (G_s, u, t); %lsim ，就是将信号u输入到传递函数中，t是时间包括时间间隔以及整体时间。
subplot (2,1,2);
plot (t,y);
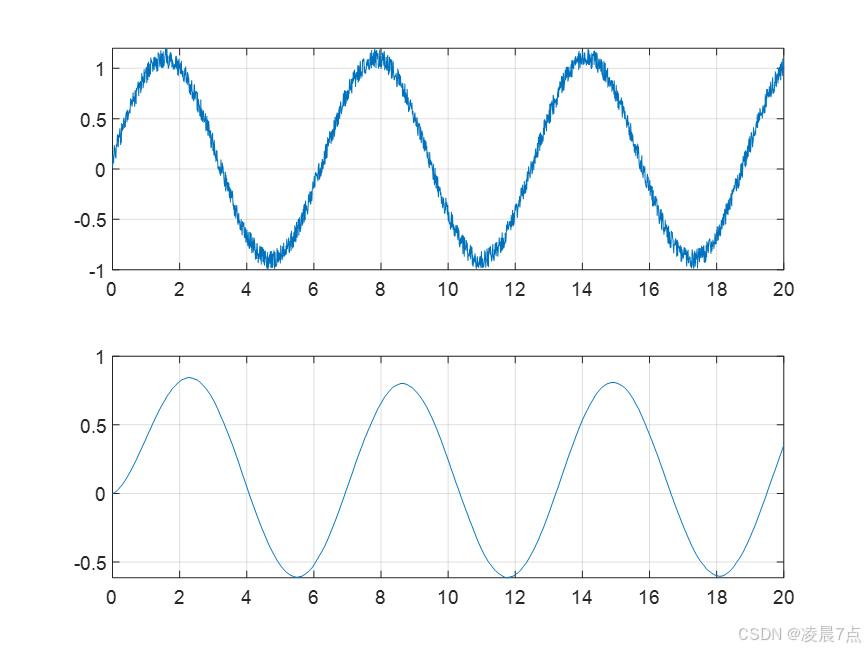
grid on;

运行结果：

上图，原始信号；
下图，通过滤波器后的信号；

学习来源：《控制之美》 $卷1$ ，王天威