提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 前言
- [1. 双指针](#1. 双指针)
-
- [1.1 移动零](#1.1 移动零)
- [1.2 复写零](#1.2 复写零)
- [2. 滑动窗口](#2. 滑动窗口)
-
- [2.1 ⻓度最⼩的⼦数组](#2.1 ⻓度最⼩的⼦数组)
- [2.2 ⽆重复字符的最⻓⼦串](#2.2 ⽆重复字符的最⻓⼦串)
- [2.3 最⼤连续 1 的个数 III](#2.3 最⼤连续 1 的个数 III)
- [3. 二分查找算法](#3. 二分查找算法)
-
- [3.1 ⼆分查找](#3.1 ⼆分查找)
- [3.2 在排序数组中查找元素的第⼀个和最后⼀个位置](#3.2 在排序数组中查找元素的第⼀个和最后⼀个位置)
- [3.3 x 的平⽅根](#3.3 x 的平⽅根)
- [3.4 ⼭峰数组的峰顶索引](#3.4 ⼭峰数组的峰顶索引)
- [3.5 寻找峰值](#3.5 寻找峰值)
- [3.6 搜索旋转排序数组中的最⼩值](#3.6 搜索旋转排序数组中的最⼩值)
- [4. 前缀和](#4. 前缀和)
-
- [4.1 【模板】⼀维前缀和](#4.1 【模板】⼀维前缀和)
- [4.2 【模板】⼆维前缀和](#4.2 【模板】⼆维前缀和)
- [4.3 寻找数组的中⼼下标](#4.3 寻找数组的中⼼下标)
- [4.4 除⾃⾝以外数组的乘积](#4.4 除⾃⾝以外数组的乘积)
- [5. 位运算](#5. 位运算)
-
- [5.1 常见位运算总结(包含5道算法题)](#5.1 常见位运算总结(包含5道算法题))
- [5.2 判断字符是否唯⼀](#5.2 判断字符是否唯⼀)
- [5.3 丢失的数字](#5.3 丢失的数字)
- [5.4 两整数之和](#5.4 两整数之和)
- [6. 模拟](#6. 模拟)
-
- [6.1 替换所有的问号](#6.1 替换所有的问号)
- [6.2 提莫攻击](#6.2 提莫攻击)
- 总结
前言
1. 双指针
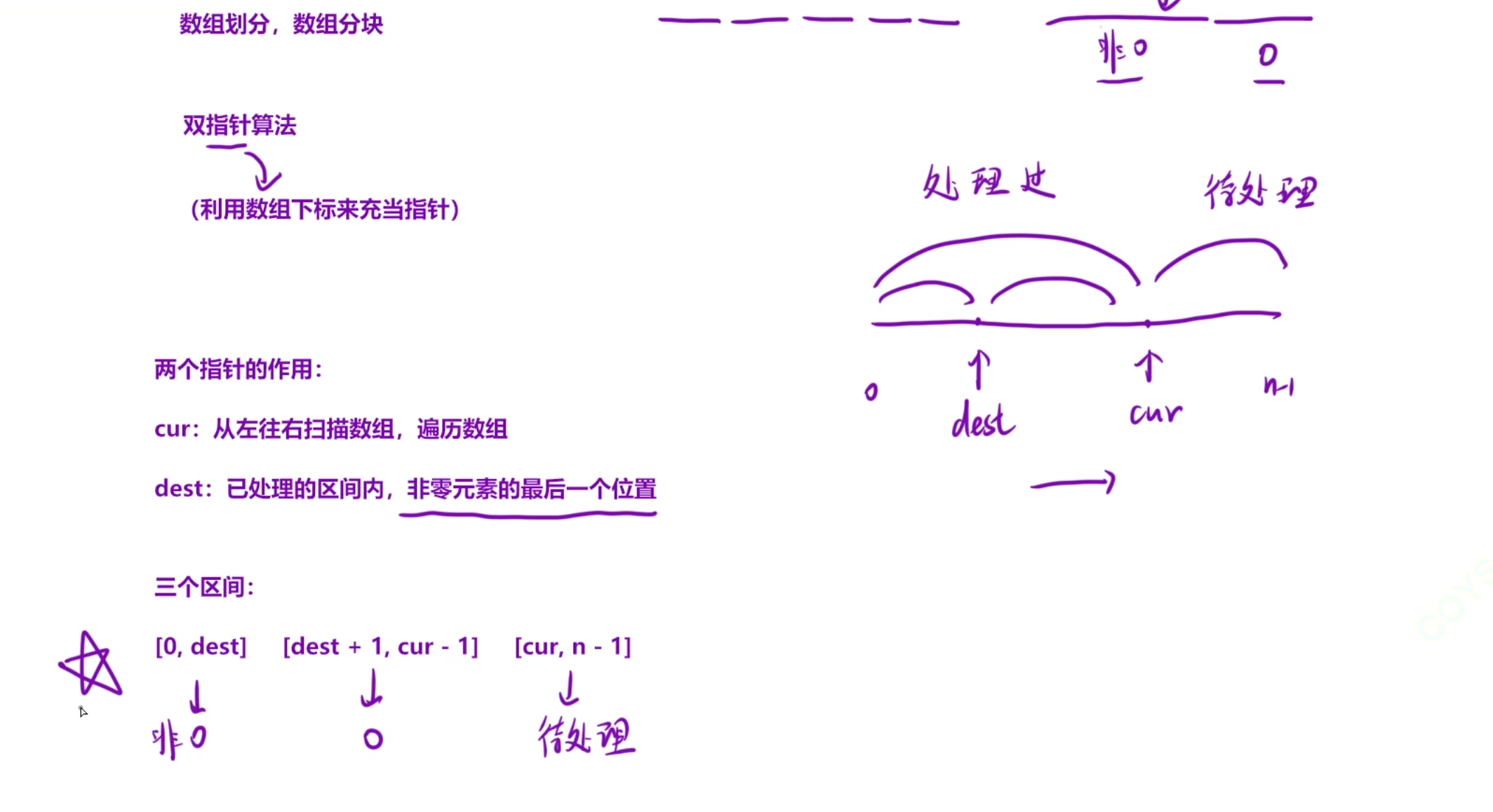
就是用两个指针,一个cur遍历,一个des来划分
1.1 移动零
算法思想就是,两个指针,一个cur,cur表示的意思是,未处理的第一个数据
des指针:des指针表示处理过的数据中的最后一个非零数据
从左往右遍历
cur初始值就是0,des初始值就是-1
cur从左往右开始遍历,如果为0,直接++,如果非零,那么就把des+1,染不黑交换des和cur的数据
java
class Solution {
public void moveZeroes(int[] nums) {
for(int cur = 0,des =-1; cur<nums.length ; cur++){
if(nums[cur]!=0){
des++;
int tmp = nums[cur];
nums[cur] = nums[des];
nums[des] = tmp;
}
}
}
}1.2 复写零

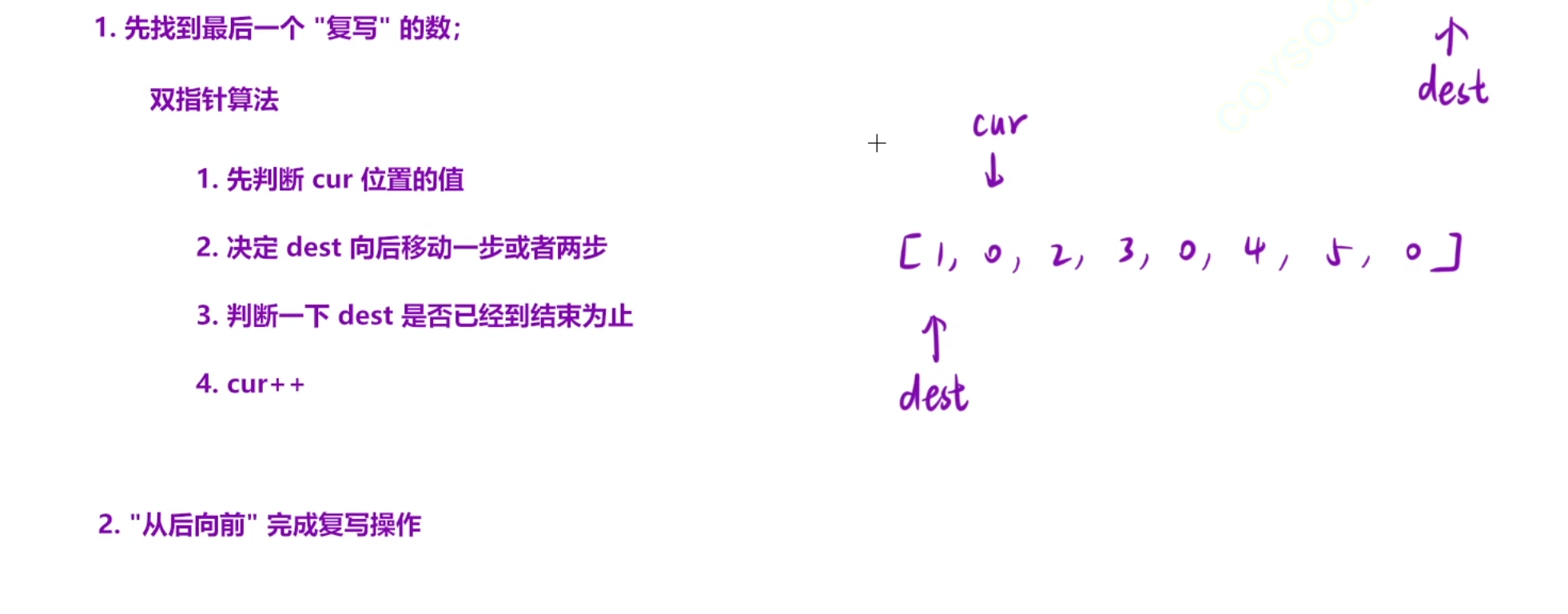
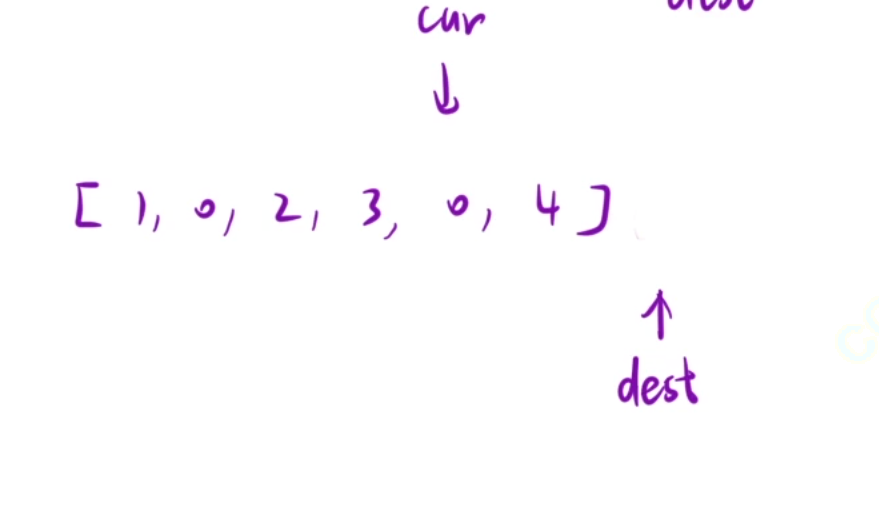
在一个数组上操作的话,从左到右可能会覆盖数据
所以我们可以从右到左,但是要先找到最后一个复写的数
怎么找打最后一个要复写的数呢
cur=0遍历数组的指针
des复写的位置,当des=n-2的时候,如果arr[cur]=0,那么des可能会越界,所以要额外判断一下
当des的位置大于等于n-1的时候,就可以直接跳出循环了,此时cur刚好是最后一个要复写的
java
class Solution {
public void duplicateZeros(int[] arr) {
//先找出最后一个要复写的数
int cur = 0;
int des = -1;
int n = arr.length;
for (;; cur++) {
if (arr[cur] == 0) {
des += 2;
} else {
des++;
}
if (des >= n - 1) {
break;
}
}
//此时的cur就是最后一个要复写的数,des可能为n-1,可能为n
//开始从右往左开始复写
//先处理临界情况
if (des == n) {
//发送这个情况的话,绝对cur指向0
arr[des - 1] = 0;
des -= 2;
cur--;
}
while (cur >= 0) {
if (arr[cur] == 0) {
arr[des] = 0;
arr[des-1] = 0;
des -= 2;
cur--;
} else {
arr[des] = arr[cur];
des--;
cur--;
}
}
}
}2. 滑动窗口
2.1 ⻓度最⼩的⼦数组
left,算出所有以left为左区间的和,只要大于target了,就是一次正确的
只要sum大于tarrget了,那么right就可以不用+了,因为已经找到了以left的满足题意的最短区间了
然后就是left右移的时候,right不用变为left+1,也可以求出left到right的和,这个和不满足大于target,那么right++,如果满足了就找到了以left的一个最短区间(满足题意)
这个就是同向双指针,也就是滑动窗口
滑动窗口也就弄好几个东西就可以了
left,right,还有窗口信息,结果
这道题的窗口信息就是sum
right一直++,就是进窗口,left也一直++,就是出窗口
什么时候更新结果呢,就是sum满足题意的时候
满足题意出窗口,出窗口然后还要一直判断是不是还满足题意,不满足题意就进窗口
步骤就是进窗口,判断, 更新结果,出窗口
java
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int n = nums.length, sum = 0, len = Integer.MAX_VALUE;
for (int left = 0, right = 0; right < n; right++) {
sum += nums[right];//进窗口
while (sum >= target) {//判断
len = Math.min(len, right - left + 1);//更新结果
sum -= nums[left++]; //出窗口
}
}
return len == Integer.MAX_VALUE ? 0 : len;//没有找到就返回0
}
}更新结果那一步是无法确定在哪里的
这一题中,必须满足sum >= target,才可以更新结果,所以更新结果就在sum >= target之后
2.2 ⽆重复字符的最⻓⼦串
子串和子数组都是连续的部分
暴力解法:可以找到以left为左区间的一个满足题意的子串
就可以优化为滑动窗口了
如何找到重复字符呢
我们可以使用哈希表
然后就是分析那几个条件了
进窗口就是把字符弄入哈希表
判断(什么时候出窗口):就是有重复字符的时候
出窗口:就是把left字符踢出哈希表
什么时候更新结果呢,当然是整个判断结束之后(没有重复字符的时候)
为什么要用滑动窗口--》暴力解法--》left和right都不回退,对一个窗口内的数据进行处理判断获取结果,连续的子区间
java
class Solution {
public int lengthOfLongestSubstring(String ss) {
int[] hash = new int[128];//hash[i],表示Ascll为i的字符出现的次数,e而且Ascll得最大值就是127
char[] s = ss.toCharArray();//将String转化为char数组
int len = 0, n = s.length;
for (int left = 0, right = 0; right < n; right++) {
hash[s[right]]++;//进窗口
while (hash[s[right]] > 1) {//有重复字符时判断
hash[s[left++]]--;//出窗口
}
//走到这里说明没有重复字符:更新结果
len = Math.max(len, right - left + 1);
}
return len;
}
}String 获取长度的方法是length()
数组获取长度的方法是length
2.3 最⼤连续 1 的个数 III
这个翻转操作代码化也太麻烦了,看看有没有什么转化的办法
可以这样转化
找出一个最长的子数组,而这个子数组0的个数不能超过k个
那么就一定可以翻转成功,而且是最长的
找子数组,还是暴力的解法,固定一个起点,然后去找终点
用一个变量来统计0的个数
然后去优化,发现left和right都可以一直前进
进不进窗口就是0的个数
判断什么时候出窗口呢(不满足条件的时候,count>key),就是0的个数太多了,
进窗口--》right++的时候,0,就+1,1的话,直接就无视
出窗口的话---》0,-1,1就无视
判断结束之后就更新结果
java
class Solution {
public int longestOnes(int[] nums, int k) {
int n = nums.length, len = 0, count = 0;
for (int left = 0, right = 0; right < n; right++) {
if (nums[right] == 0)
count++;//进窗口
while (count > k) {//判断
if (nums[left++] == 0)
count--;//出窗口
}
len = Math.max(len, right - left + 1);//更新结果
}
return len;
}
}更新结果那里是必须到达的,所以不能因为为1,就直接跳过这层循环
3. 二分查找算法
3.1 ⼆分查找
就是可以把数组分为两段,然后舍去一段,这个就可以用二分
根据规律把数组分为两段
这个就叫做两段性,分段最好就是一半一半的分,中间的分段是最好的时间复杂度
细节问题;
循环结束的条件:left>right

java
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if(nums[mid] > target){
right = mid -1 ;
}else if(nums[mid] < target){
left = mid + 1;
}else{
return mid;
}
}
return -1;
}
}这个就差不多是朴素版本的模版了
先定义左右指针
left + (right - left) / 2
2说明就是中点
这串代码的意思是,right-left是数组长度,除以2就是一半长度,所以left+(right - left) / 2就是中点,改为3就是三分之一点
然后就是 int mid = left + (right - left) / 2;
与 int mid = left + (right - left+1) / 2;
的区别
如果是奇数个数的话,那么mid就是中点那个值
如果是偶数个数的话,那么+1的mid就是偏右的那个,没有+1的就是偏左的那个
3.2 在排序数组中查找元素的第⼀个和最后⼀个位置
非递减的意思就是要么增加,要么不变
暴力查找就是on的复杂度
如果是朴素版本的二分,找不到起点和终点,只能找到那一个点
二段性:
查找左端点:划分为两个部分,一个小于target,一个大于等于target
所以我们要找的是大于等于target的最左边的那个

细节处理
循环条件:left<right , 因为当left=right的时候,就是最终结果
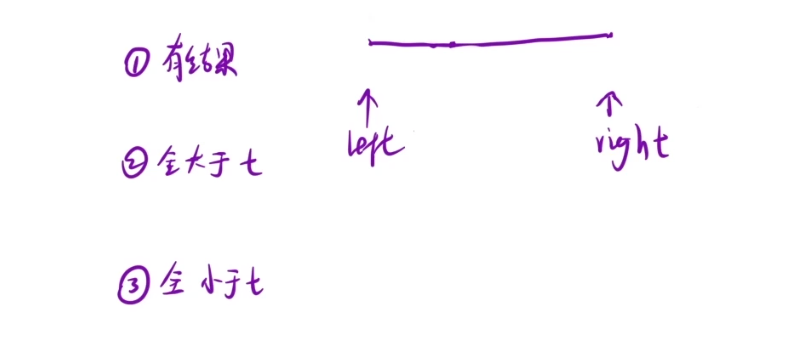
而且如果为left<=right,那么就会死循环
求中点操作:
left+(right-left)/2
left+(right-left+1)/2
只能用第一个,因为如果只有最后两个挨着的数据的时候,只有left+(right-left)/2求出的中点才会让left和right移动,left+(right-left+1)/2可能会让right一直无法移动
然后是右端点的处理
二段性:左边小于等于target,右边大于targe
所以mid<=target,left=mid
mid>target , right= mid-1
while(left<right)
然后是中点的处理
left+(right-left+1)/2
因为为了使只有两个的时候,left和right都可以移动,而left=mid,可能不会移动,所以一定要偏右才好
记忆:左端点的话,中点偏左 ,left+1
最终left和right都是指向最后的结果
java
class Solution {
public int[] searchRange(int[] nums, int target) {
int[] ret = new int[2];
ret[0] = ret[1] = -1 ;
if(nums.length == 0 ){
return ret;
}
int left = 0 , right = nums.length - 1;
//先求左端点
while(left < right){
int mid = left + (right-left)/2;
if(nums[mid] < target){
left = mid + 1;
}else{
right = mid;
}
}
//此时left=right
if(nums[left] != target){
return ret;
}
ret[0] = left;
left = 0 ; right = nums.length - 1;
//在求右端点
while(left < right){
int mid = left + (right-left+1)/2;
if(nums[mid] > target){
right = mid - 1;
}else{
left = mid;
}
}
ret[1] = left;
return ret;
}
}3.3 x 的平⽅根
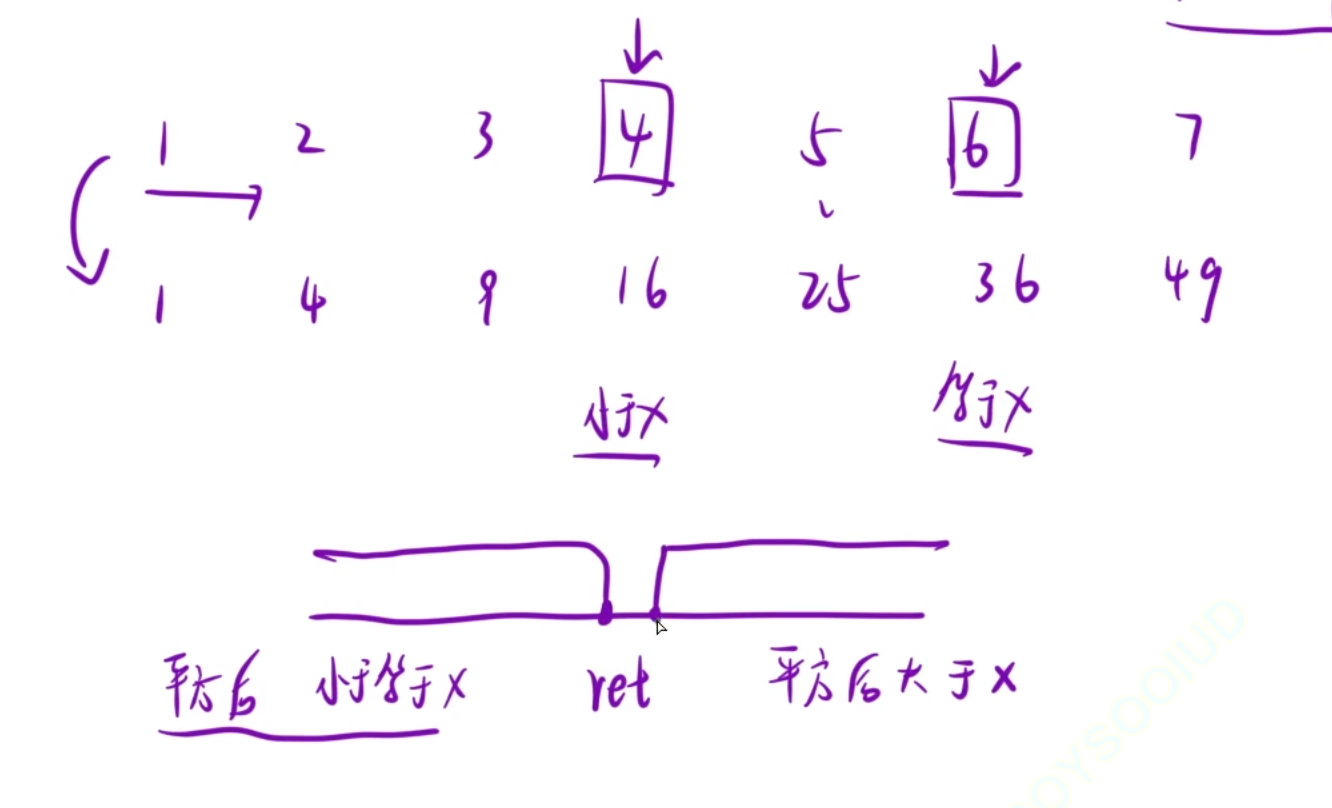
有二段性
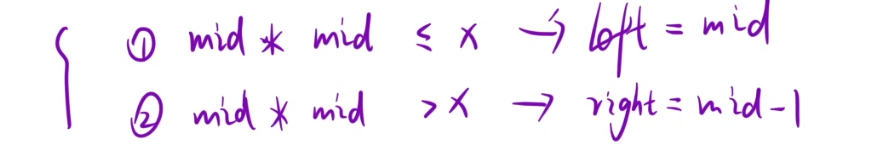
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
在1~8中寻找,找到的每个数平方与8进行比较
我们要寻找的是,平方小于等于8的,然后这些中的最大值,平方大于8的全部不要
这个就相当于找右端点了
target就是8
因为0 <= x <= 2^31 - 1范围比较大,所以我们用long
java
class Solution {
public int mySqrt(int x) {
long left = 0, right = x;
while (left < right) {
long mid = left + (right - left + 1) / 2;
if (mid * mid <= x) {
left = mid;
} else {
right = mid - 1;
}
}
return (int) left;
}
}3.4 ⼭峰数组的峰顶索引
只有一个峰值
暴力解法:从前往后扫描,第一个递减的数就是那个峰值
二段性
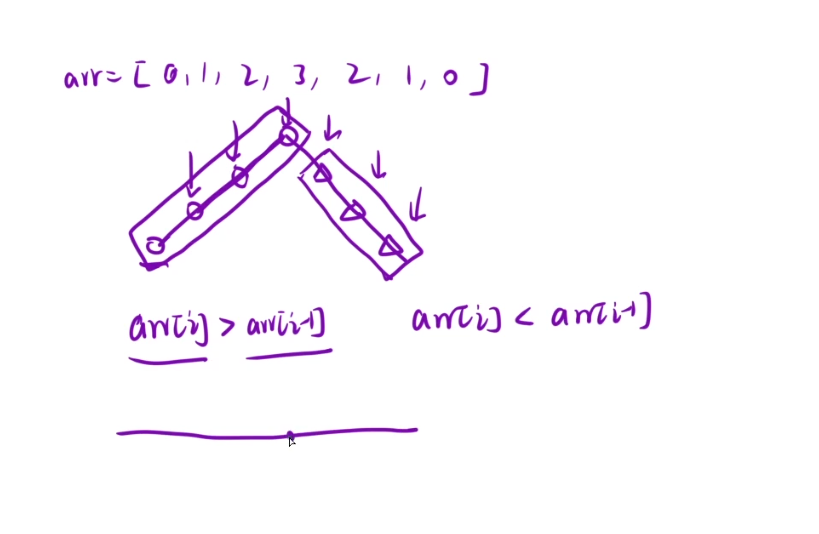
我们要找的是左边区间的最后一个值,相当于找右端点
左区间的特性是arr[i]>arr[i-1]
右区间的特性是arr[i]<arr[i-1]
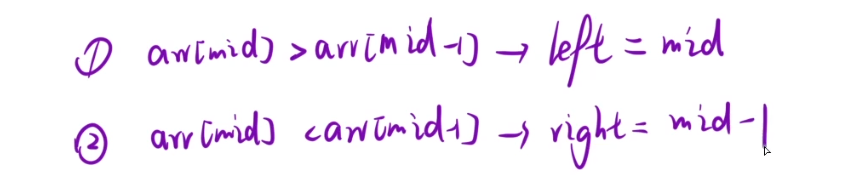
mid满足左区间的特性说明mid在左边,所以left=mid
,left不能=mid+1,因为mid可能为最终结果
java
class Solution {
public int peakIndexInMountainArray(int[] arr) {
int left =0 ,right = arr.length ;
while(left < right){
int mid = left + (right - left + 1) / 2;
if(arr[mid] > arr[mid-1]){
left = mid ; //mid在左边
}else{
right = mid - 1;
}
}
return left;
}
}先分析二段性,根据题意,看能不能在最终结果那里,把数组分为两段,两段的属性刚好不一样,根据这两段属性分析left和right该怎么随mid变化
,最后如果有-1,那么 (right - left + 1)
如果有+1,那么 (right - left )
3.5 寻找峰值
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。这个的意思就是要使用二分算法
你可以假设 nums[-1] = nums[n] = -∞ 。
暴力解法:从第一位置就下降,那么第一位置就是峰值
然后往后面遍历,一直上升,然后下降的话,那么下降的位置就是一个峰值,如果上升走到最后一个位置的话,最后一个位置就是峰值o(n)
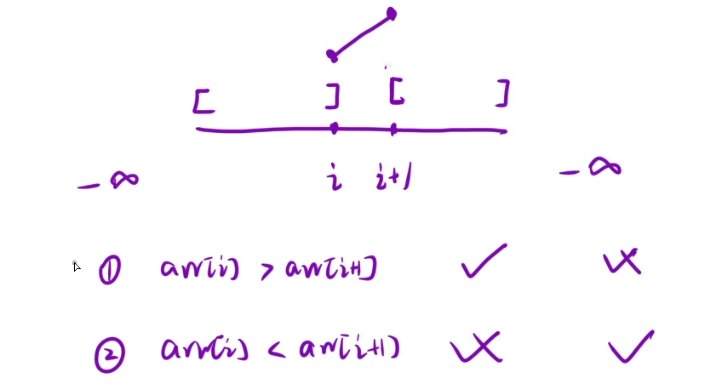
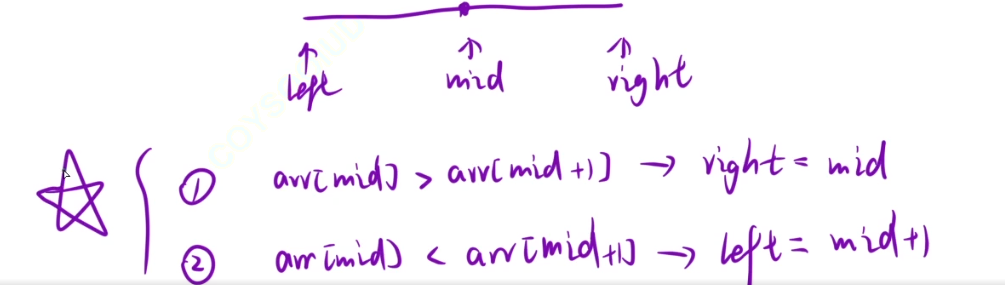
当arr[mid]>arr[mid+1]时,因为arr[-1]=负无穷,所以mid的左边就一定有峰值,所以right-=mid
当arr[mid]<arr[mid+1],那么右边就一定有峰值,所以可以缩小区间,left=mid+1
因为有+1.所以(right - left )
java
class Solution {
public int findPeakElement(int[] nums) {
int left = 0 , right = nums.length - 1;
while(left < right){
int mid = left + (right - left) / 2 ;
if(nums[mid] > nums[mid+1]){
right = mid ;
}else if(nums[mid] < nums[mid+ 1]){
left = mid + 1;
}
}
return left;
}
}这个就是把区间往高处压缩,虽然不一定是最高的
3.6 搜索旋转排序数组中的最⼩值
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。说明是二分
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
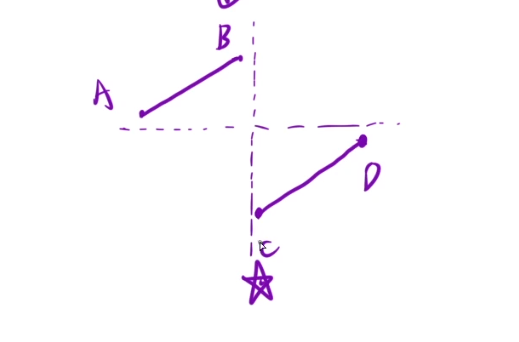
二段性:
左边每个都大于D,右边每个都小于等于D
找出C
arr[mid]>D: 说明mid在左区间AB left = mid + 1
arr[mid] <=D : 说明mid在右区间CD right = mid
其中D=arr[n-1]
java
class Solution {
public int findMin(int[] nums) {
int left = 0 , right = nums.length -1 ;
int target = nums[right] ;
while(left < right){
int mid = left + (right - left) / 2 ;
if(nums[mid] > target){
left = mid + 1;
}else{
right = mid ;
}
}
return nums[left];
}
}4. 前缀和
4.1 【模板】⼀维前缀和
暴力解法的话,时间复杂度是o(n*m),那么就是10^10,这个绝对会超时的
前缀和:
- 先预处理一个前缀和数组:dp[i]:表示1~i的所有元素的和
dp[i] =dp[i-1] + arr[i] - 开始使用,sum[i,j] = dp[j] - dp[i-1]
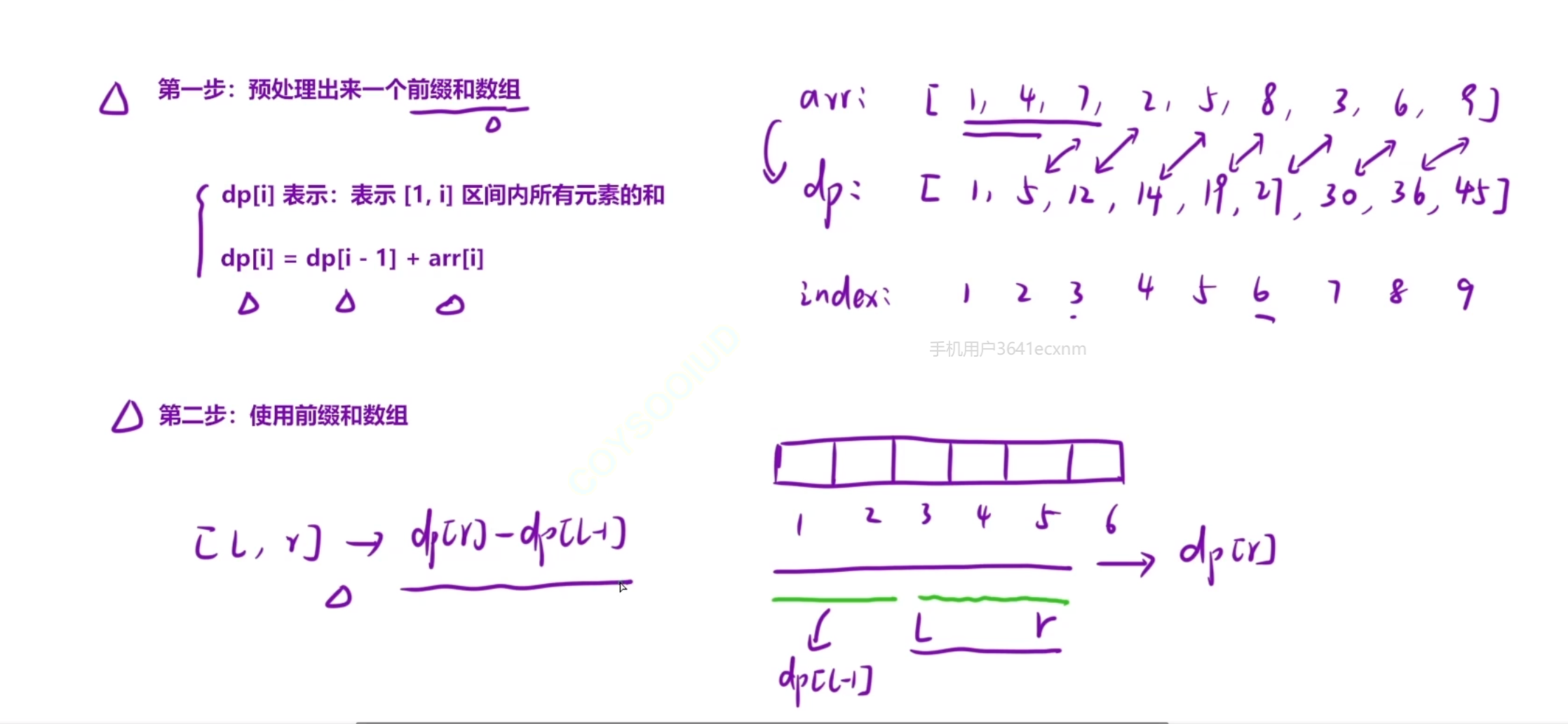
注意这里要从1开始计数,因为如果从0开始的话,dp[0-1]不存在
从1开始的话,dp[1-1]是存在的,而且为0
java
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt() , m = in.nextInt();
int a[] =new int [n+1];
//先求出前缀和
long dp[] = new long[n+1];//用long,防止越界
for(int i=1;i<=n;i++){
a[i] = in.nextInt();
dp[i] = dp[i-1] + a[i];
}
while(m > 0){
int i =in.nextInt() , j =in.nextInt();
System.out.println(dp[j] - dp[i-1]);
m--;
}
}
}nextInt就是相当于C语言的scanf
4.2 【模板】⼆维前缀和
暴力解法:o(nnq)
预处理前缀和矩阵
dp[i][j] : 从[1][1]到[i][j]的所有的和

dp[i][j] = dp[i][j-1] + dp[i-1][j] + arr[i][j] -dp[i][j]
然后是使用
x1,y1 x2,y2
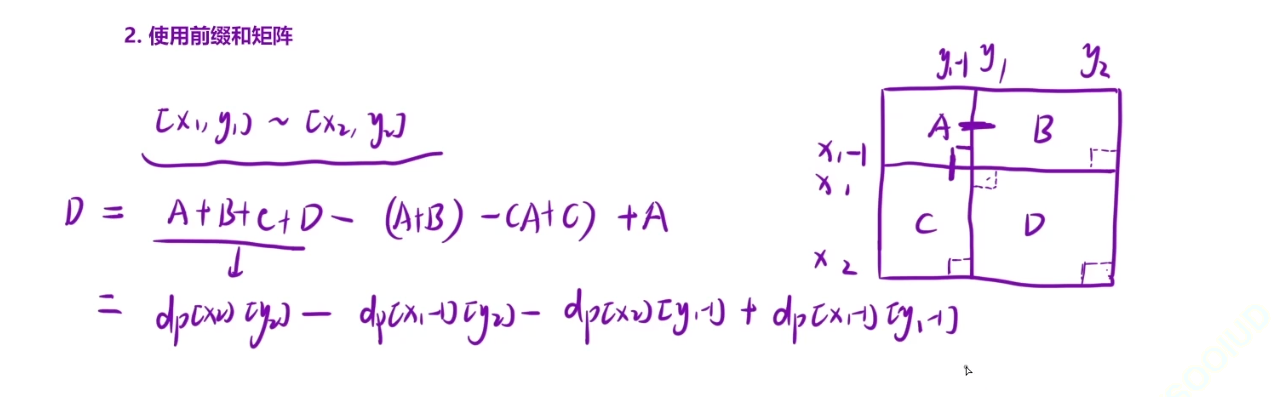
java
import java.util.Scanner;
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt() , m = in.nextInt() ,q = in.nextInt();
int arr[][] =new int[n+1][m+1];
long[][] dp = new long[n+1][m+1];
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
arr[i][j] = in.nextInt();
dp[i][j] = dp[i-1][j] + dp[i][j-1]- dp[i-1][j-1] + arr[i][j];
}
}
while(q>0){
int x1 = in.nextInt() ,y1 = in.nextInt(),x2 = in.nextInt(),y2 = in.nextInt();
System.out.println(dp[x2][y2] + dp[x1-1][y1-1] - dp[x2][y1-1] - dp[x1-1][y2]);
q--;
}
}
}4.3 寻找数组的中⼼下标
涉及连续的区间求和--》前缀和
我们这里搞两个数组,一个前缀和数组,一个后缀和数组
f和g
f[i]表示0到i-1数组的和
g[i]: 表示i+1到n-1的和
f[i] = f[i-1] +arr[i-1]
g[i] = g[i+1] +arr[i+1]
所以判断f[i]==g[i]?
然后还要考虑端点的问题,初始化一下,比如f[0]=0,g[n-1]=0
java
class Solution {
public int pivotIndex(int[] nums) {
int n = nums.length ;
int[] f =new int[n];//0~i-1,f[0]=0
int[] g = new int[n];//g[n-1]=0,i+1~n-1
for(int i=1;i<n;i++){
f[i] = f[i-1] + nums[i-1];
}
for(int i=n-2;i>=0;i--){
g[i] =g[i+1] + nums[i+1];
}
for(int i=0;i<n;i++){
if(f[i] == g[i]){
return i;
}
}
return -1;
}
}4.4 除⾃⾝以外数组的乘积
就是弄一个前缀积和后缀积
f和g
f[i]表示0~i-1的积
f[i] =f[i-1] * nums[i-1]
g[i]表示i+1~N-1的积
g[i] = g[i+1] * nums[i+1]
f[0]=1,g[n-1]=1
java
class Solution {
public int[] productExceptSelf(int[] nums) {
int n = nums.length;
int[] f = new int[n];
int[] g = new int[n];
f[0] = g[n-1] =1;
for(int i=1;i<n;i++){
f[i] = f[i-1] * nums[i-1];
}
for(int i=n-2;i>=0;i--){
g[i] = g[i+1] * nums[i+1];
}
int[] ret = new int[n];
for(int i=0;i<n;i++){
ret[i] = f[i] * g[i];
}
return ret;
}
}5. 位运算
5.1 常见位运算总结(包含5道算法题)



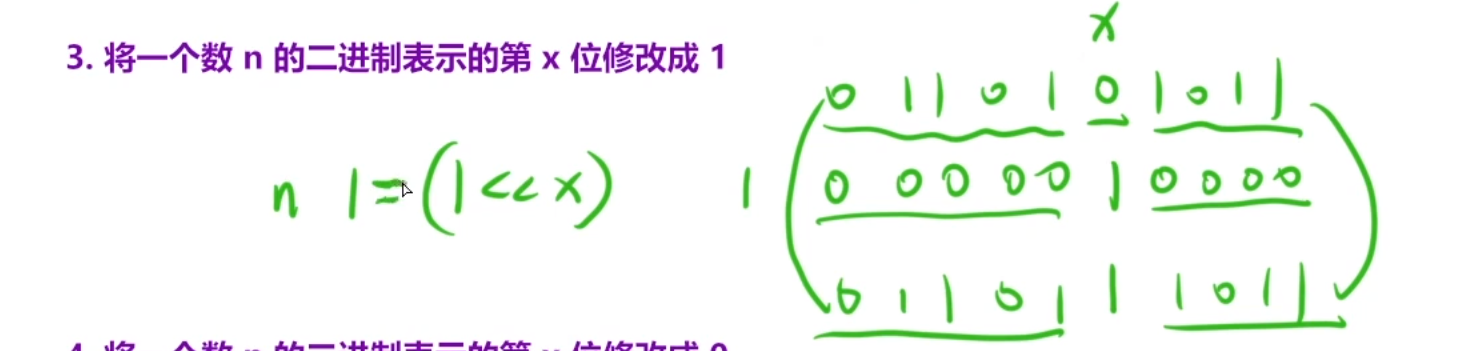
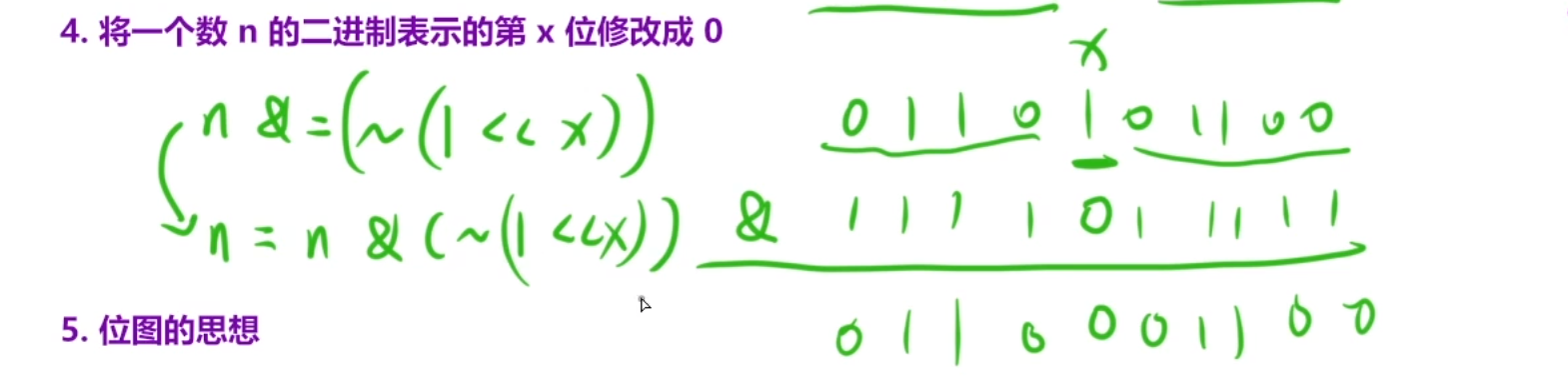
一个正数要变为负数,只需要所有位按位取反再加1
或者符号位变1,然后其余位按位取反,在+1
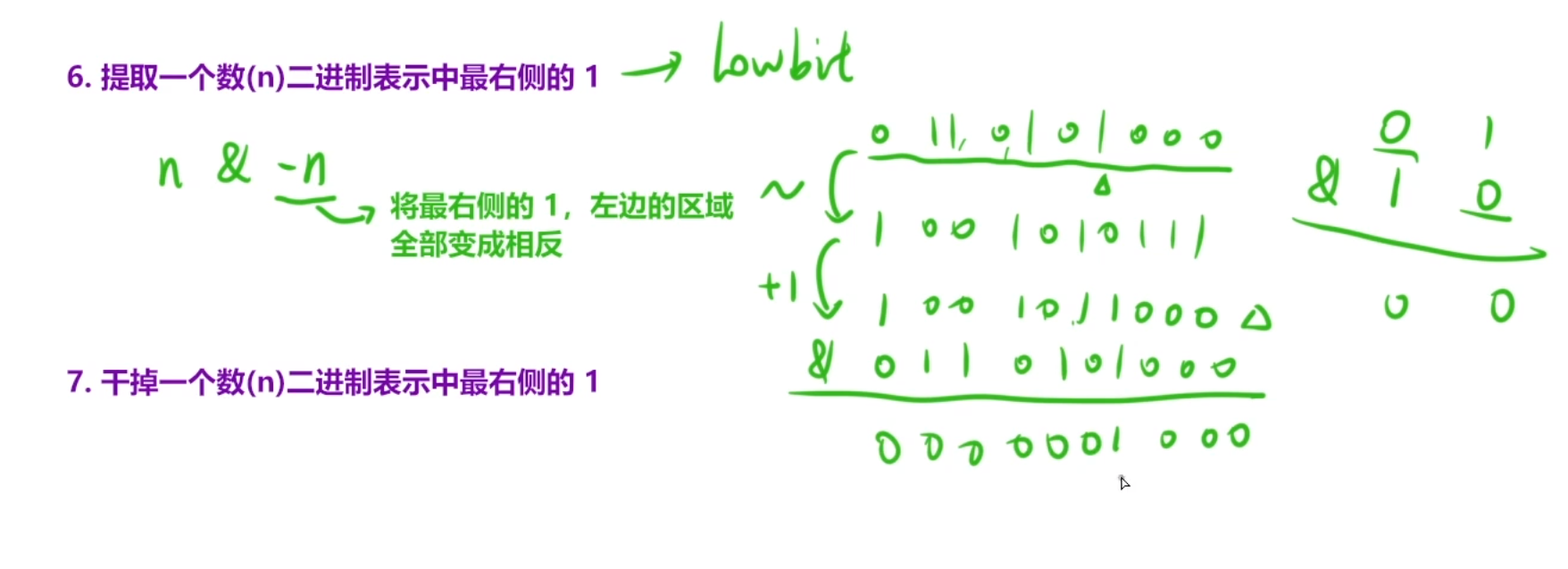
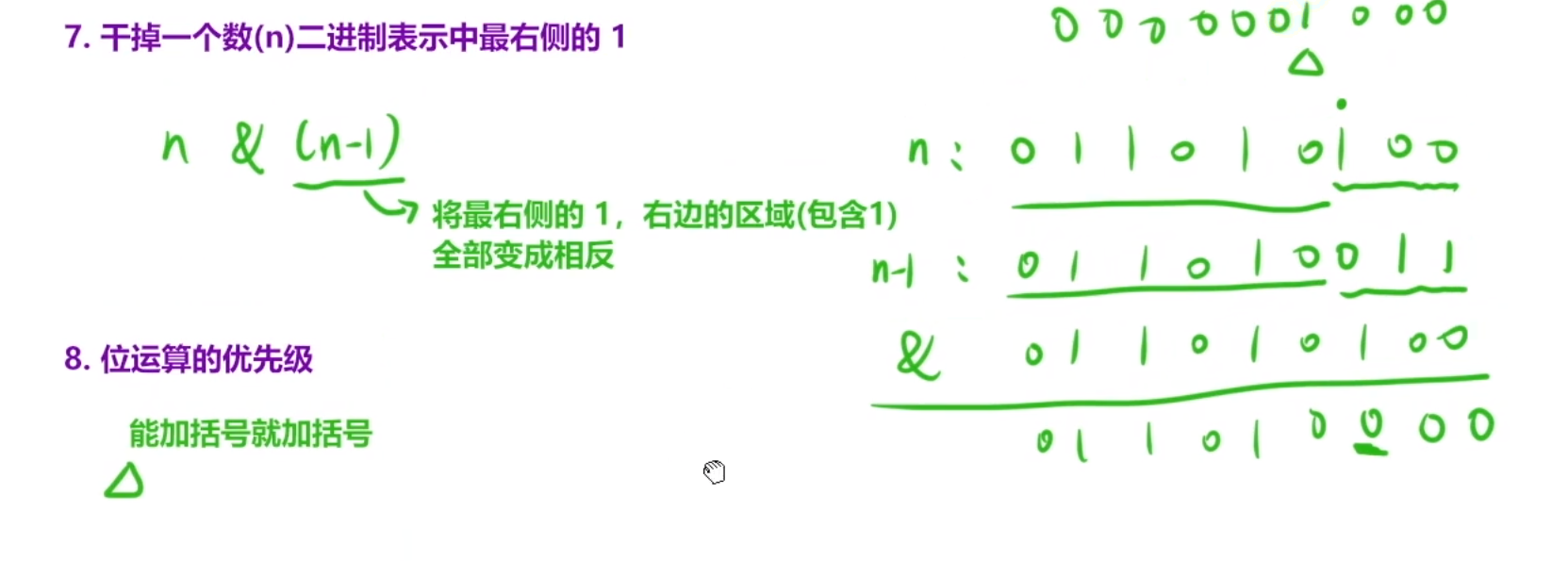
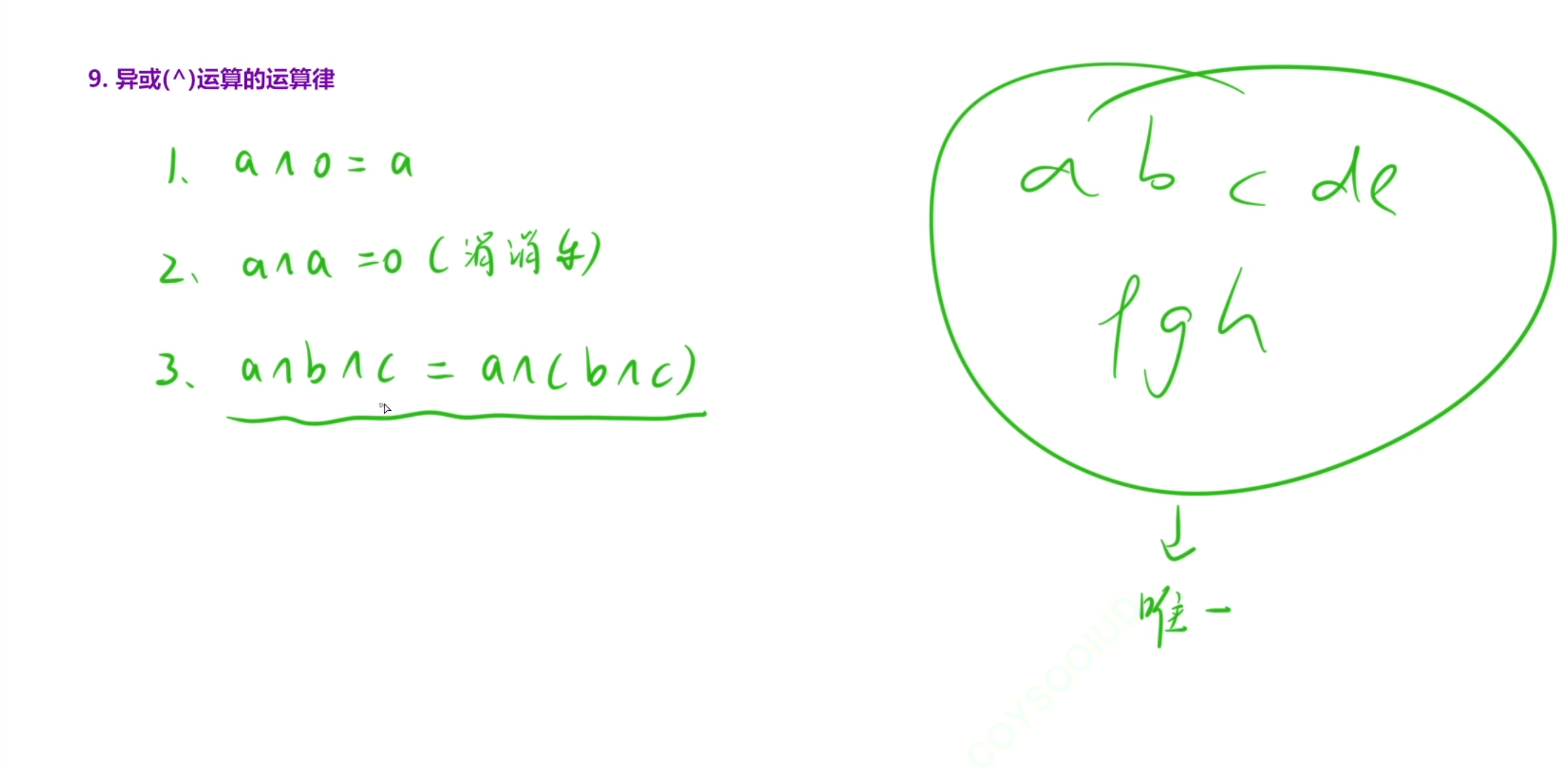
因为是无进位相加的,所以一定是可以满足交换律和结合律的
5.2 判断字符是否唯⼀
解法一:可以用一个hash表,因为只有小写字母,所以我们用一个26大小的数组
解法二:还可以使用位图的思想,因为一个int只有32位,让0号代表a,1号代表b
优化点:抽屉原理,因为一共有26个,所以如果长度大于26的话,那么一定有重复的
java
class Solution {
public boolean isUnique(String astr) {
if(astr.length()>26){
return false;
}
int hash = 0;
for(int i=0;i<astr.length();i++){
int x = astr.charAt(i) - 'a';
//然后判断x位上有没有这个数据,就是变没变1
if( ((hash>>x)&1) == 1){
return false;
}
//x位不为1,说明这个是新的,还没有重复的,所以把x位变为1
hash |= (1<<x);
}
return true;
}
}5.3 丢失的数字
方法一:哈希表
方法二:高斯求和,0~n的和 - 数组的和
方法三:位运算,0~n 与 数组的数字一起异或就可以了
java
class Solution {
public int missingNumber(int[] nums) {
int ret = 0;
for(int x : nums) ret ^= x;
for(int i=0;i<=nums.length;i++) ret^=i;
return ret;
}
}5.4 两整数之和

不用加法减法的话,就用位运算了
异或运算 : 无进位相加
只有1和1才有进位,按位与就有进位了,就知道哪里有进位了
又因为进位在前面一位,所以还要左移一位
然后把进位和异或的结果相加--》重复循环
直到进位不存在

java
class Solution {
public int getSum(int a, int b) {
while(b!=0){//进位不为0的时候就一直循环相加
int x = a ^ b ;//无进位结果
int y = (a & b)<<1;//进位
a = x ;
b = y;
}
return a;
}
}6. 模拟
就是比葫芦画瓢
6.1 替换所有的问号
java
class Solution {
public String modifyString(String s) {
char[] c = s.toCharArray();
int n = c.length;
for(int i=0;i< n; i++){
if(c[i]=='?'){
for(char j ='a';j<='z';j++){
if( ( (i==0) || (j!=c[i-1]) ) && ( (i==n-1) || (j!=c[i+1]) ) ){
c[i] = j;
}
}
}
}
return String.valueOf(c);
}
}6.2 提莫攻击
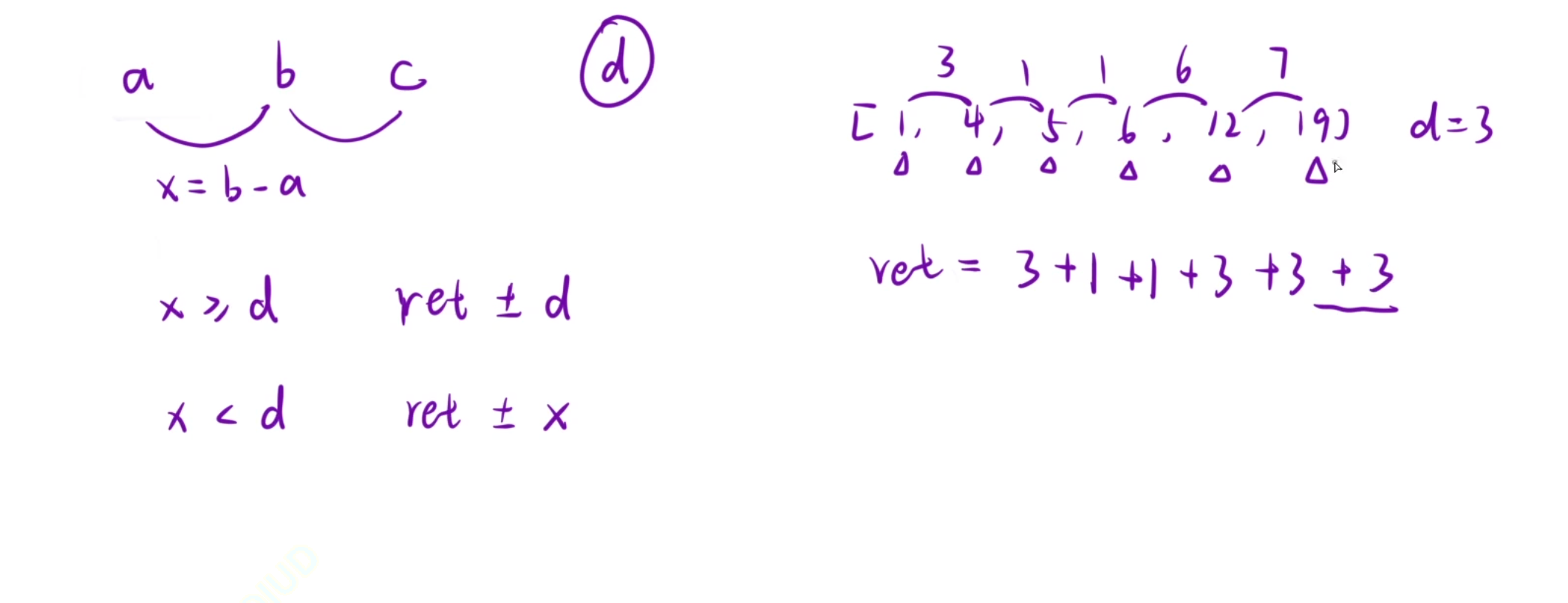
攻击的两个时间点间隔x,如果大于d,那么总时间就+d,如果小于d,那么就+x
还有就是最后一个时间点直接+d
java
class Solution {
public int findPoisonedDuration(int[] timeSeries, int duration) {
int ret = 0;
for(int i=1;i< timeSeries.length ;i++){
int x = timeSeries[i] - timeSeries[i-1];//算出每个间隔
if(x>duration) {
ret += duration;
}else{
ret += x;
}
}
return ret += duration;
}
}