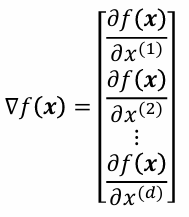2.3 Prelim: Gradients and Gradient descent
2.3 预备知识:梯度与梯度下降
2.4 Prelim: Gradient Descent Code
2.4 预备知识:梯度下降代码
2.5 Prelim: Convexity
2.5 预备知识:凸性
梯度下降
- Gradient(梯度)
- [梯度下降算法 Gradient Descent](#梯度下降算法 Gradient Descent)
- [Convexity of function 函数的凸性](#Convexity of function 函数的凸性)
Gradient(梯度)
什么是 Gradient(梯度)?
梯度 = 导数 = 函数某一点的变化率
在多维函数中,梯度是一个向量,表示函数在某点沿各个方向的最速上升方向,也就是各个自变量的偏导数集合向量。
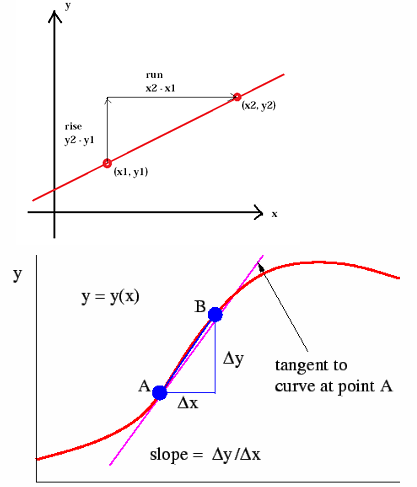
梯度公式
实例:
f ( x ( 1 ) , x ( 2 ) ) = ( x ( 1 ) ) 2 + ( x ( 2 ) ) 2 f(x^{(1)}, x^{(2)}) = (x^{(1)})^2 + (x^{(2)})^2 f(x(1),x(2))=(x(1))2+(x(2))2
∂ f ∂ x ( 1 ) = 2 x ( 1 ) \frac{\partial f}{\partial x^{(1)}} = 2x^{(1)} ∂x(1)∂f=2x(1)
∂ f ∂ x ( 2 ) = 2 x ( 2 ) \frac{\partial f}{\partial x^{(2)}} = 2x^{(2)} ∂x(2)∂f=2x(2)
梯度为:
∇ f ( x ) = [ ∂ f ( x ) ∂ x ( 1 ) ∂ f ( x ) ∂ x ( 2 ) ] \nabla f(\mathbf{x}) = \begin{bmatrix} \frac{\partial f(\mathbf{x})}{\partial x^{(1)}} \\[6pt] \frac{\partial f(\mathbf{x})}{\partial x^{(2)}} \end{bmatrix} ∇f(x)= ∂x(1)∂f(x)∂x(2)∂f(x)
梯度下降算法 Gradient Descent
In order to find the minima of a function, keep taking steps along a direction opposite to the gradient of the function. 为了找到函数的最小值,需要沿着与函数梯度相反的方向不断移动。
梯度下降算法公式
w ( k + 1 ) = w ( k ) − α ∂ f ( w k ) ∂ w k w^{(k+1)} = w^{(k)} - \alpha \frac{\partial f(w_k)}{\partial w_k} w(k+1)=w(k)−α∂wk∂f(wk)
α \alpha α 是无限接近0的步长
w ( k + 1 ) w^{(k+1)} w(k+1) 是自变量点
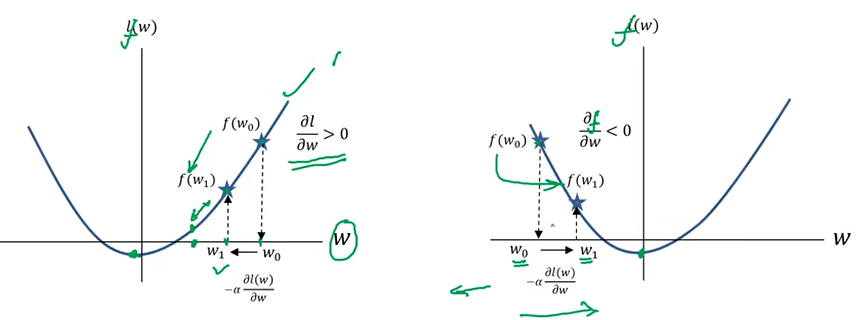
目的是找到这个函数的极小值,所以采用这个公式。
斜率为正, w k w^{k} wk被减,变小,后退。斜率为负数, w k w^{k} wk被加,变大,往前走。所以恰好利用斜率的相反数,实现了极值的寻找。这就是梯度下降算法。
梯度下降算法代码
javascript
import numpy as np
# 梯度下降函数
def gd(fxn, dfxn, w0=0.0, lr=0.01, eps=1e-4, nmax=1000, history=True):
"""
参数说明:
fxn: 目标函数 f(w),输入 w 返回函数值
dfxn: 梯度函数 ∇f(w),输入 w 返回梯度值
w0: 初始位置
lr: 学习率 (步长)
eps: 收敛阈值(当步长小于此值时停止迭代)
nmax: 最大迭代次数
history: 是否保存每一步的历史记录(用于画图)
返回值:
w: 最终的 w 值
converged: 是否收敛
H: 历史记录(每步 w 和 f(w))
"""
H = [] # 用于存储历史记录
w = w0 # 初始化 w
# 如果需要记录历史,先保存初始位置
if history:
H = [[w, fxn(w)]]
for i in range(nmax):
dw = -lr * dfxn(w) # 梯度下降更新公式 dw = -α * ∇f(w)
# 如果步长小于 eps,认为已经收敛
if np.linalg.norm(dw) < eps:
break
# 如果需要记录历史,保存当前点和下一个点的函数值
if history:
H.append([w + dw, fxn(w + dw)])
# 更新 w
w = w + dw
# 判断是否收敛
converged = np.linalg.norm(dw) < eps
return w, converged, np.array(H)
# 主函数
if __name__ == '__main__':
import matplotlib.pyplot as plt
# 定义目标函数 f(w)
def myfunction(w):
# z = (w - 0.5)^2 + 2 + sin(4w)
z = (w - 0.5)**2 + 2 + np.sin(4*w)
return z
# 定义梯度函数 ∇f(w)
def mygradient(w):
# dz/dw = 2*(w - 0.5) + 4*cos(4w)
dz = 2*(w - 0.5) + 4*np.cos(4*w)
return dz
# 在 [-3, 3] 之间生成 100 个等间距点
wrange = np.linspace(-3, 3, 100)
# 随机生成初始 w0
w0 = np.min(wrange) + (np.max(wrange) - np.min(wrange)) * np.random.rand()
# 调用梯度下降函数
w, c, H = gd(myfunction, mygradient, w0=w0, lr=0.01, eps=1e-4, nmax=1000, history=True)
# 画出目标函数曲线
plt.plot(wrange, myfunction(wrange))
# 画出梯度曲线
plt.plot(wrange, mygradient(wrange))
plt.legend(['f(w)', 'df(w)']) # 两条线的图例
plt.xlabel('w')
plt.ylabel('value')
# 显示收敛的步数
s = 'Convergence in ' + str(len(H)) + ' steps'
if not c:
s = 'No ' + s
plt.title(s)
# 画出迭代点(黑点)
plt.plot(H[0,0], H[0,1], 'ko', markersize=10) # 初始点
plt.plot(H[:,0], H[:,1], 'r.-') # 迭代轨迹
plt.plot(H[-1,0], H[-1,1], 'kk', markersize=10) # 最终点
plt.grid()
plt.show()Convexity of function 函数的凸性
严格凸性:如果在函数上的"任意"两点之间画一条线,且该线始终位于函数上方,则该函数称为凸函数。
凸函数只有一个最小值
下面三个图中,只有第一个是convex。第二个和第三个都是Non-convex。
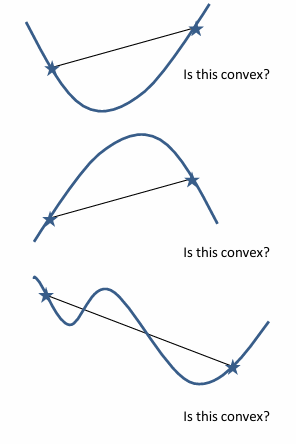
第三个图通过梯度下降算法可以得到局部最小值,但取决于初始点的位置。
我们对凸函数感兴趣,是因为凸函数可以使用梯度下降算法,得到极小值。无论从哪里开始,无论是什么位置,我们都可以保证会收敛到全局最优解。