LeetCode Day6 -- 图

[1. 图](#1. 图)

[1.1 python实现：邻接表、邻接矩阵](#1.1 python实现：邻接表、邻接矩阵)

[1.2 应用场景](#1.2 应用场景)

[2. BFS & DFS](#2. BFS & DFS)

[2.1 广度优先搜索BFS](#2.1 广度优先搜索BFS)

[2.2 深度优先搜索DFS](#2.2 深度优先搜索DFS)

3.Leetcode

[3.1 图的连通性问题](#3.1 图的连通性问题)

[（1）841 钥匙和房间](#（1）841 钥匙和房间)

[（2）547 省份数量](#（2）547 省份数量)

[（3）1466 重新规划路线](#（3）1466 重新规划路线)

[（4）200 岛屿数量](#（4）200 岛屿数量)

[3.2 BFS解决二维矩阵中的问题](#3.2 BFS解决二维矩阵中的问题)

[（1）1926 迷宫中离入口最近的出口](#（1）1926 迷宫中离入口最近的出口)

[（2）994 腐烂的橘子](#（2）994 腐烂的橘子)

[3.3 带权图](#3.3 带权图)

[（1）399 除法求值](#（1）399 除法求值)

[3.4 拓扑排序](#3.4 拓扑排序)

[（1）207 课程表](#（1）207 课程表)

1. 图

1.1 python实现：邻接表、邻接矩阵

（1）邻接表 （常用：节省空间，适合稀疏图）

python 复制代码

graph = {
    'A': ['B', 'C'],       # 无向图邻居
    'B': ['A', 'C', 'D'],
    'C': ['A', 'B'],
    'D': ['B']
}

""" 带权图的邻接表 """
weighted_graph = {
    'A': {'B': 2, 'C': 4},
    'B': {'C': 1, 'D': 7}
}

（2）邻接矩阵 （适合稠密图）

python 复制代码

matrix = [
    [0, 1, 1, 0],   # A的邻居：B、C
    [1, 0, 1, 1],   # B的邻居：A、C、D
    [1, 1, 0, 0],   # C的邻居：A、B
    [0, 1, 0, 0]    # D的邻居：B
]

1.2 应用场景

场景	问题类型	实现思路
路径规划	最短路径	Dijkstra（非负权）、Bellman-Ford（负权）
社交网络	好友推荐	BFS查找K度好友，社区检测（DFS连通分量）
任务调度	依赖排序	拓扑排序（有向无环图）
网络分析	广播消息	BFS模拟消息扩散
AI寻路	状态转移	DFS回溯（如迷宫）

2. BFS & DFS

2.1 广度优先搜索BFS

（1）过程： 逐层遍历，用队列实现。

（2）应用场景：最短路径（无权图）、层级遍历、拓扑排序（Kahn算法）、扩散传播等

python 复制代码

from collections import deque

def bfs(graph, start):
    visited = set([start])
    queue = deque([start])

    while queue:
        vertex = queue.popleft()
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)
    return visited  # 返回所有可达节点

2.2 深度优先搜索DFS

（1）过程 ：递归深入路径，用栈实现。

（2）应用场景：路径存在性检测（如迷宫）、拓扑排序（有向无环图）、连通分量统计、环检测（递归栈）、回溯问题等

python 复制代码

""" 递归版 """
def dfs_recursive(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs_recursive(graph, neighbor, visited)
    return visited

""" 迭代版（栈实现）"""
def dfs_iterative(graph, start):
    visited = set()
    stack = [start]
    while stack:
        vertex = stack.pop()
        if vertex not in visited:
            visited.add(vertex)
            stack.extend(reversed(graph[vertex]))  # 保持原顺序
    return visited

3.Leetcode

3.1 图的连通性问题

（1）841 钥匙和房间

有 n 个房间，房间按从 0 到 n - 1 编号。最初，除 0 号房间外的其余所有房间都被锁住。你的目标是进入所有的房间。然而，你不能在没有获得钥匙的时候进入锁住的房间。当你进入一个房间，你可能会在里面找到一套 不同的钥匙 ，每把钥匙上都有对应的房间号，即表示钥匙可以打开的房间。你可以拿上所有钥匙去解锁其他房间。给你一个数组 rooms 其中 rooms[i] 是你进入 i 号房间可以获得的钥匙集合。如果能进入所有房间返回 true，否则返回 false。

BFS方案：

python 复制代码

from collections import deque
class Solution(object):
    def canVisitAllRooms(self, rooms):
        """
        :type rooms: List[List[int]]
        :rtype: bool
        """
        n=len(rooms)
        visited=[False]*n
        ## 从0号房开始BFS
        quene = deque([0])
        visited[0]=True

        while quene:
            cur_room = quene.popleft()  ##当前房间号
            for key in rooms[cur_room]: ## 遍历当前房间内的钥匙
                if not visited[key]:
                    visited[key]=True
                    quene.append(key)
        return all(visited)

DFS方案：

python 复制代码

n=len(rooms)
        visited=[False]*n

        def dfs(room):
            visited[room]=True          ## 能开当前room，visited=true
            for key in rooms[room]:     ## 看当前room中有哪些key
                if not visited[key]:    ## 如果key对应的房间没被开过，去开当前key对应的房间
                    dfs(key)
        
        dfs(0)  ## 从0号房开始DFS
        return all(visited)

（2）547 省份数量

省份的定义是一组直接或间接相连的城市（即一个连通分量）→ 求无向图中连通分量的个数

BFS方案：

python 复制代码

n=len(isConnected)
visited=[False]*n
count=0

for i in range(n):
    if not visited[i]:  ## 找到未标记省份
        count+=1
        quene=deque([i])  ## 找省份内的其他城市（找整个连通分量）
        while quene:
            city=quene.popleft()
            for neighbor in range(n):
                if isConnected[city][neighbor]==1 and not visited[neighbor]:
                    visited[neighbor]=True
                    quene.append(neighbor)
return count

DFS方案：

python 复制代码

class Solution(object):
    def findCircleNum(self, isConnected):
        """
        :type isConnected: List[List[int]]
        :rtype: int
        """
        n = len(isConnected)
        visited = [False]*n
        count = 0

        def dfs(city):
            visited[city]=True
            ## 遍历该城市的所有邻居
            for neighbor in range(n):
                ## 如果是邻居且未被访问过，继续递归，直到找到这一条完整的连通分量
                if isConnected[city][neighbor]==1 and not visited[neighbor]:
                    visited[neighbor]=True
                    dfs(neighbor)

        for i in range(n):
            if not visited[i]:
                count+=1    ## 找到未标记的省份
                dfs(i)      ## 找到该省份内的所有城市
        return count

（3）1466 重新规划路线

重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

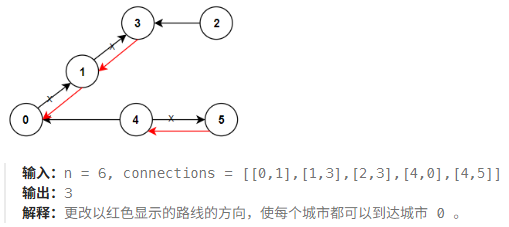
1. 构建图结构：创建一个无向图，包含所有节点及其连接关系

2. 方向判断：在遍历过程中，对每条边：

-- 如果原始方向是从父节点指向当前节点，说明方向正确

-- 如果原始方向是从当前节点指向父节点，说明方向需要反转

BFS方案：

python 复制代码

from collections import deque
class Solution(object):
    def minReorder(self, n, connections):
        """
        :type n: int
        :type connections: List[List[int]]
        :rtype: int
        """
        graph = [[] for _ in range(n)]
        edges = set()           ## 存放边的方向
        for i, j in connections:
            graph[i].append(j)
            graph[j].append(i)
            edges.add((i,j))    ## 需要翻转的原始有向边(i→j)

        count=0
        visited=[False]*n
        visited[0]=True
        quene=deque([0])

        while quene:
            i=quene.popleft()
            for j in graph[i]:      ## j是当前节点的邻居
                if not visited[j]:  
                    visited[j]=True
                    quene.append(j)
                    if (i,j) in edges:
                        count+=1

        return count

DFS方案：

python 复制代码

class Solution(object):
    def minReorder(self, n, connections):
        """
        :type n: int
        :type connections: List[List[int]]
        :rtype: int
        """
        graph = [[] for _ in range(n)]
        for i, j in connections:
            graph[i].append((j, True))      ## i→j：背离0节点的方向，需要翻转
            graph[j].append((i, False))     ## j→i：无需翻转
        print(graph)

        visited=[False]*n
        visited[0]=True
        self.count=0

        def dfs(node):
            for neighbor, need_flip in graph[node]:
                if not visited[neighbor]:
                    visited[neighbor]=True
                    if need_flip:
                        self.count+=1
                    dfs(neighbor)

        dfs(0)
        return self.count

（4）200 岛屿数量

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

python 复制代码

from collections import deque
class Solution(object):
    def numIslands(self, grid):
        """
        :type grid: List[List[str]]
        :rtype: int
        """
        m, n= len(grid), len(grid[0])   ## m-行，n-列
        directions=[(0,1), (0,-1), (1,0), (-1,0)]
        visited = [[False]*n for _ in range(m)]
        island=0

        for i in range(m):
            for j in range(n):
                if grid[i][j]=='1':   ## 发现未访问的陆地
                    island+=1   
                    grid[i][j]='0'    ## 标记为水 → 相当于已访问
                    ## 找和当前陆地连接的其他陆地（找连通分量，看能形成多大的岛）
                    quene=deque()
                    quene.append((i,j))
                    while quene:
                        row, col = quene.popleft()
                        for dr,dc in directions:    ## 往四个方向延伸
                            cur_row, cur_col = dr+row, dc+col

                            ## 检查新位置是否是有效的陆地
                            if 0<=cur_row<m and 0<=cur_col<n and grid[cur_row][cur_col]=='1':
                                grid[cur_row][cur_col]='0'
                                quene.append((cur_row,cur_col))

        return island

3.2 BFS解决二维矩阵中的问题

（1）1926 迷宫中离入口最近的出口

1. 初始化：从入口点开始 BFS

2. 遍历方向：每次可移动上、下、左、右四个方向

3. 边界条件：不能进入墙（"+"）、不能超出迷宫边界、已访问过的点不再访问

4. 终止条件：到达迷宫边界上的空格子（且不是入口点）

python 复制代码

from collections import deque
class Solution(object):
    def nearestExit(self, maze, entrance):
        """
        :type maze: List[List[str]]
        :type entrance: List[int]
        :rtype: int
        """
        m=len(maze)     ## 行
        n=len(maze[0])  ## 列
        directions=[(-1,0),(1,0),(0,-1),(0,1)]  ## 下一步要尝试的方向（上下左右）
        visited=[[False]*n for _ in range(m)]   ## 创建m*n的visited存储访问标记
        steps=0
        quene=deque()

        start_row, start_col = entrance[0], entrance[1] ## 初始位置
        visited[start_row][start_col]=True
        quene.append((start_row, start_col, steps))

        while quene:
            row, col, steps = quene.popleft()

            """ 判断是否到达出口（非起点的边界处）"""
            is_boundary = (row==0 or row==m-1 or col==0 or col==n-1)
            is_start = (row==start_row and col==start_col)

            """ 若找到出口 """
            if is_boundary and not is_start:
                return steps
            
            """ 没找到出口，继续向上下左右四个方向分别查找 """
            for dr,dc in directions:
                cur_row, cur_col = dr+row, dc+col   ## 下一步的位置
                """ 下一步的位置是否在范围内 """
                if 0<=cur_row<m and 0<=cur_col<n:
                    """ 若是范围内还没走过的地方，看能不能走 """
                    if not visited[cur_row][cur_col] and maze[cur_row][cur_col]=='.':
                        visited[cur_row][cur_col]=True
                        quene.append(((cur_row, cur_col, steps+1)))
                    
        return -1

（2）994 腐烂的橘子

每分钟，腐烂的橘子周围 4 个方向上相邻的新鲜橘子都会腐烂。返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能，返回 -1 。

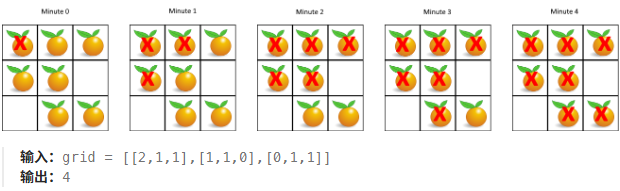
**1. 时间统计：**该按层处理，同一层的橘子同时腐烂（同1分钟）

**2. 访问标记：**不需要独立visited数组，可直接用grid值判断（grid=2 → visited=True）

python 复制代码

from collections import deque
class Solution(object):
    def orangesRotting(self, grid):
        """
        :type grid: List[List[int]]
        :rtype: int
        """
        m, n = len(grid), len(grid[0])  ## 行,列
        visited=[[False]*n for _ in range(m)]
        directions=[(0,1), (0,-1), (1,0), (-1,0)]
        minutes=-1      ## 初始为-1，第一次循环变为0
        fresh_nums=0    ## 新鲜橘子数
        quene=deque()

        for i in range(m):
            for j in range(n):
                if(grid[i][j]==2):      ## 腐烂橘子入队（可能不止一个）
                    quene.append((i,j))    
                elif(grid[i][j]==1):    ## 统计新鲜橘子数目
                    fresh_nums += 1

        """ 本身就没有新鲜的橘子，直接返回0 """
        if fresh_nums==0:     
            return 0

        while quene:
            """ 当前有size个腐烂橘子，同时发力腐烂新鲜的 """
            size = len(quene)   
            for _ in range(size):
                row, col= quene.popleft()         

                for dr,dc in directions:
                    cur_row, cur_col = dr+row, dc+col

                    if 0<=cur_row<m and 0<=cur_col<n:
                        if grid[cur_row][cur_col]==1:
                            grid[cur_row][cur_col]=2
                            quene.append((cur_row,cur_col))
                            fresh_nums -= 1
            """ 四个方向同时被腐烂 → 走完四个方向时间才会增加 """
            minutes += 1    

        return minutes if fresh_nums==0 else -1

3.3 带权图

（1）399 除法求值

本质上是带权有向图路径查找。

实现方案：

构建图：使用字典，key为节点，value为另一个字典（邻居和对应的权重）。

对于每个查询，在图中搜索路径，并计算乘积。

如果路径不存在或者节点不在图中，返回-1.0。

BFS方案：

python 复制代码

from collections import deque
from collections import defaultdict
class Solution(object):
    def calcEquation(self, equations, values, queries):
        """
        :type equations: List[List[str]]
        :type values: List[float]
        :type queries: List[List[str]]
        :rtype: List[float]
        """

        """ step1:构建带权有向图 """
        graph = defaultdict(dict)
        node = set()
        for (a,b),val in zip(equations, values):
            graph[a][b]=val
            graph[b][a]=1.0 / val
            node.add(a)
            node.add(b)

        """ step2:处理每个查询 """
        result=[]

        for i,j in queries:
            """ 情况1-未定义查询变量 """  
            if i not in node or j not in node:
                result.append(-1.0)
                """ 跳过当前查询的后续处理，继续下一个查询 """
                continue
            """ 情况2-相同查询变量 """
            if i==j:
                result.append(1.0)
                continue
            """ 情况3-需要按路径查找的查询变量 """
            quene=deque()    ## BFS队列：(当前节点, 累积乘积)    
            visited=set()    ## 记录已访问节点
            
            quene.append((i,1.0))
            visited.add(i)
            found=False        ## 标记是否找到路径

            while quene and not found:    ## 有节点待处理且未找到路径
                cur_node, cur_product = quene.popleft()
                for neighbor, value in graph[cur_node].items():
                    """ 情况3-1：找到目标节点对应的路径 """
                    if neighbor==j:    
                        result.append(cur_product*value)
                        found=True
                        """ 跳出当前邻居循环，不需要再找其他邻居了 """
                        break
                    """ 情况3-2：还没找到目标节点，但还有邻居没访问"""
                    if neighbor not in visited:
                        visited.add(neighbor)
                        quene.append((neighbor,cur_product*value))

            """ 情况4：遍历完还没找到路径 """
            if not found:
                result.append(-1.0)

        return result

DFS方案：

python 复制代码

from collections import deque
from collections import defaultdict
class Solution(object):
    def calcEquation(self, equations, values, queries):
        """
        :type equations: List[List[str]]
        :type values: List[float]
        :type queries: List[List[str]]
        :rtype: List[float]
        """
      
        graph = defaultdict(dict)
        nodes = set()
        for (a,b),val in zip(equations, values):
            graph[a][b]=val
            graph[b][a]=1.0/val
            nodes.add(a)
            nodes.add(b)

        def dfs(i, j, product, visited):
            """ 递归终止条件：找到目标节点，返回乘积和 """
            if i==j:
                return product

            """ 若还没找到目标节点 """
            visited.add(i)      ## # 标记当前节点已访问
            for neighbor,value in graph[i].items():
                if neighbor not in visited: ## 跳过已访问节点
                    # 递归搜索：累积路径乘积
                    result = dfs(neighbor,j,product*value,visited)
                    # 如果在当前路径中找到解，直接返回结果
                    if result != -1.0:
                        return result
            """ 没找到目标路径 """
            return -1.0

        result=[]
      
        for i,j in queries:
            if i not in nodes or j not in nodes:
                result.append(-1.0)
            elif i==j:
                result.append(1.0)
            else:
                visited=set()   ## 每次查询都要创建新的visited集合
                result.append(dfs(i,j,1.0,visited))
        return result

3.4 拓扑排序

（1）207 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。在选修某些课程之前需要一些先修课程。先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则必须先学习课程 bi 。例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

核心是判断有向图 是否存在环。给定课程的先修关系（prerequisites），构建一个有向图：

节点：每门课程 (0 到 numCourses-1)

边 ：prerequisites[i] = [a, b]表示 b → a（先修 b 才能学 a）

需要检测这个有向图是否是 有向无环图(DAG)。

如果可以完成所有课程学习，则图无环；如果存在环则无法完成。

BFS方案：Kahn算法，根据节点的入度判断

1. 初始化：

（1）构建 邻接表 表示图（2）维护 节点入度数组（前驱课程数）

2. 入队入度为零节点：不需要先修课程即可学习的课程入队

3. BFS处理：

（1）每次出队一门课程，标记为已学，并将该课程所有后续课程的入度减1

（2）若某课程入度为零，则入队

4. 结果判断：

成功学习的课程数等于总课程数 → 可行，否则存在循环依赖 → 不可行

python 复制代码

from collections import deque, defaultdict
class Solution(object):
    def canFinish(self, numCourses, prerequisites):
        """
        :type numCourses: int
        :type prerequisites: List[List[int]]
        :rtype: bool
        """

        """ step1:构建有向图（邻接表形式）+计算节点入度 """
        graph = defaultdict(list)
        indegree = [0] * numCourses

        for course, pre_course in prerequisites:
            graph[pre_course].append(course)    # 边：pre_course → course
            indegree[course] += 1               # course入度+1(course先修课+1)

        """ step2:初始化队列，入度为0的course入队 """
        quene=deque()
        for i in range(numCourses):
            if indegree[i]==0:
                quene.append(i)
        
        """ step3:BFS处理 """
        visited = 0     ## 标记已学习的课程数
        while quene:
            cur_course=quene.popleft()      ## 当前可学的课程
            visited+=1  
            for neighbor in graph[cur_course]:  
                indegree[neighbor]-=1       ## 当前课程的后置课程入度-1
                if indegree[neighbor]==0:
                    quene.append(neighbor)  ## 入度为0就能开始学了

        return visited == numCourses

DFS方案：检测是否有环

1. 状态标记 ：0=未访问，1=访问中，2=已访问

2. DFS递归：

（1）进入节点时标记为"访问中"

（2）递归处理所有邻居

（3）若遇到"访问中"节点 → 发现环

（4）若所有邻居无环，回溯标记"已访问"

3. 全局检测：

为每个未访问节点启动DFS，任一环则返回不可行

python 复制代码

""" step1:构建图 """
        graph = defaultdict(list)
        for course, pre_course in prerequisites:
            graph[pre_course].append(course)

        """ step2:DFS检测环 
            0: 未访问（还未进行DFS）
            1: 访问中（当前DFS路径中正在访问该节点）
            2: 已访问（该节点的DFS已经完成，没有发现环，是安全节点）
        """
        visited = [0]*numCourses   

        def find_circle(course):
            """ 递归终止条件 """
            if visited[course]==1:  return True     ## 已在当前DFS路径中 → 发现环!
            if visited[course]==2:  return False    ## 已经是安全节点 → 无需重复检查

            visited[course]=1   ## 标记当前节点为"访问中"(1)

            """ 递归检测所有后续课程 """
            for neighbor in graph[course]:
                if find_circle(neighbor):
                    return True
            
            """ 回溯标记：将当前节点设为"安全节点"(2) """
            visited[course] = 2
            return False

        for i in range(numCourses):
            if visited[i]==0:   ## 每次只需要处理还没访问过的节点
                if find_circle(i):
                    return False
        return True