2025-08-18:最大化游戏分数的最小值。用go语言,给你一个长度为 n 的数组 points 和一个整数 m。另有一个大小为 n 的数组 gameScore,初始时所有元素均为 0。你从位置 -1(在索引 0 之前的一个位置)开始,最多可以进行 m 次移动。每次移动必须向左或向右走一步(索引增加 1 或减少 1),并且每次进入某个索引 i 时,就把 points[i] 的值累加到 gameScore[i] 上。可以多次经过同一位置,累计多次加分。注意:第一次走动后,你的位置必须始终保持在数组索引范围内(即后续不能移出 0 到 n−1 的范围)。
目标是设计最多 m 步的移动序列,使得最终 gameScore 中的最小值尽可能大。返回能达到的最大最小值。
2 <= n == points.length <= 5 * 10000。
1 <= points[i] <= 1000000。
1 <= m <= 1000000000。
输入:points = [2,4], m = 3。
输出:4。
解释:
一开始,下标 i = -1 且 gameScore = [0, 0].
| 操作 | 下标 i | gameScore |
|---|---|---|
| 增加 | 0 | [2, 0] |
| 增加 | 1 | [2, 4] |
| 减少 | 0 | [4, 4] |
gameScore 中的最小值为 4 ,这是所有方案中可以得到的最大值,所以返回 4 。
题目来自力扣3449。
示例分析
以 points = [2, 4] 和 m = 3 为例:
- 初始位置:
i = -1,gameScore = [0, 0]。 - 第一次移动:向右到
i = 0,gameScore = [2, 0](移动 1)。 - 第二次移动:向右到
i = 1,gameScore = [2, 4](移动 2)。 - 第三次移动:向左到
i = 0,gameScore = [4, 4](移动 3)。 最终gameScore的最小值为4,这是可以得到的最大值。
解题思路
我们需要找到一个移动序列,使得 gameScore 的最小值最大化。直接枚举所有可能的移动序列是不现实的,因为 m 可以非常大(1e9)。因此,我们需要采用更高效的方法。
二分搜索
观察到我们可以对"最小值的最大值"进行二分搜索:
- 设
low是我们希望gameScore的最小值能达到的值。 - 我们需要验证是否存在一个移动序列,使得
gameScore的所有元素至少为low,且移动步数不超过m。 - 如果存在这样的序列,则可以尝试更大的
low;否则需要尝试更小的low。
验证函数
对于给定的 low,我们需要计算最少需要多少步才能让所有 gameScore[i] >= low:
- 对于每个
points[i],计算至少需要进入i多少次才能让gameScore[i] >= low。即k_i = ceil(low / points[i])。 - 移动序列可以看作是在数组上来回移动。每次从
i移动到i+1或i-1需要一步。 - 最优的移动序列通常是"左右横跳"的模式:从
0开始,向右走到n-1,然后向左走到0,再向右走,等等。 - 对于每个
i,k_i是进入i的次数。我们需要计算覆盖所有k_i的最小步数。
计算最小步数
- 对于第一个元素
points[0],需要进入k_0次。每次进入0需要从-1开始(第一次),或者从1回来。 - 对于其他元素
points[i],需要进入k_i次。每次进入i可以从i-1或i+1过来。 - 最优策略是尽可能利用"往返"移动:从
0开始,向右走到i,然后向左走回0,这样可以在较少的步数内多次访问0和i。
具体验证步骤
对于给定的 low:
- 计算每个
i的k_i = ceil(low / points[i])。 - 初始时在
-1,第一次移动到0需要 1 步。 - 对于
i > 0,从i-1到i需要 1 步,从i到i-1也需要 1 步。 - 总步数是
sum_{i} (2 * k_i - 1)减去一些优化(例如最后一个元素不需要完全往返)。 - 如果总步数
<= m,则low可行。
时间复杂度
- 二分搜索的范围是
[0, (m + 1) / 2 * max(points))],因为最多可以访问每个位置(m + 1) / 2次(每次往返需要 2 步,可以访问一个位置最多(m + 1) / 2次)。 - 二分搜索的时间复杂度是
O(log(right)),其中right是(m + 1) / 2 * max(points)。 - 每次验证需要遍历
points数组,时间复杂度是O(n)。 - 总时间复杂度是
O(n * log(right))。
空间复杂度
- 除了输入和输出,我们只需要常数空间来存储中间变量。
- 总空间复杂度是
O(1)。
示例验证
以 points = [2, 4] 和 m = 3 为例:
- 二分搜索
low的范围是[0, (3 + 1)/2 * 4] = [0, 8]。 - 验证
low = 4:k_0 = ceil(4 / 2) = 2,k_1 = ceil(4 / 4) = 1。- 移动序列:
-1 -> 0(步数 1,gameScore = [2, 0])。0 -> 1(步数 2,gameScore = [2, 4])。1 -> 0(步数 3,gameScore = [4, 4])。
- 总步数
3 <= 3,low = 4可行。
- 验证
low = 5:k_0 = ceil(5 / 2) = 3,k_1 = ceil(5 / 4) = 2。- 最少需要
2 * 3 - 1 + 2 * 2 - 1 = 5 + 3 = 8步(实际可能需要更少,但显然8 > 3),不可行。
- 因此最大可行的
low是4。
总结
- 使用二分搜索确定最大的
low,使得存在移动序列让gameScore的最小值至少为low。 - 验证函数计算最少需要多少步才能让所有
gameScore[i] >= low。 - 时间复杂度:
O(n * log(right))。 - 空间复杂度:
O(1)。
Go完整代码如下:
go
package main
import (
"fmt"
"slices"
"sort"
)
func maxScore(points []int, m int) int64 {
right := (m + 1) / 2 * slices.Min(points)
ans := sort.Search(right, func(low int) bool {
// 二分最小的不满足要求的 low+1,即可得到最大的满足要求的 low
low++
left := m
pre := 0
for i, p := range points {
k := (low-1)/p + 1 - pre // 还需要操作的次数
if i == len(points)-1 && k <= 0 { // 最后一个数已经满足要求
break
}
k = max(k, 1) // 至少要走 1 步
left -= k*2 - 1 // 左右横跳
if left < 0 {
return true
}
pre = k - 1 // 右边那个数顺带操作了 k-1 次
}
return false
})
return int64(ans)
}
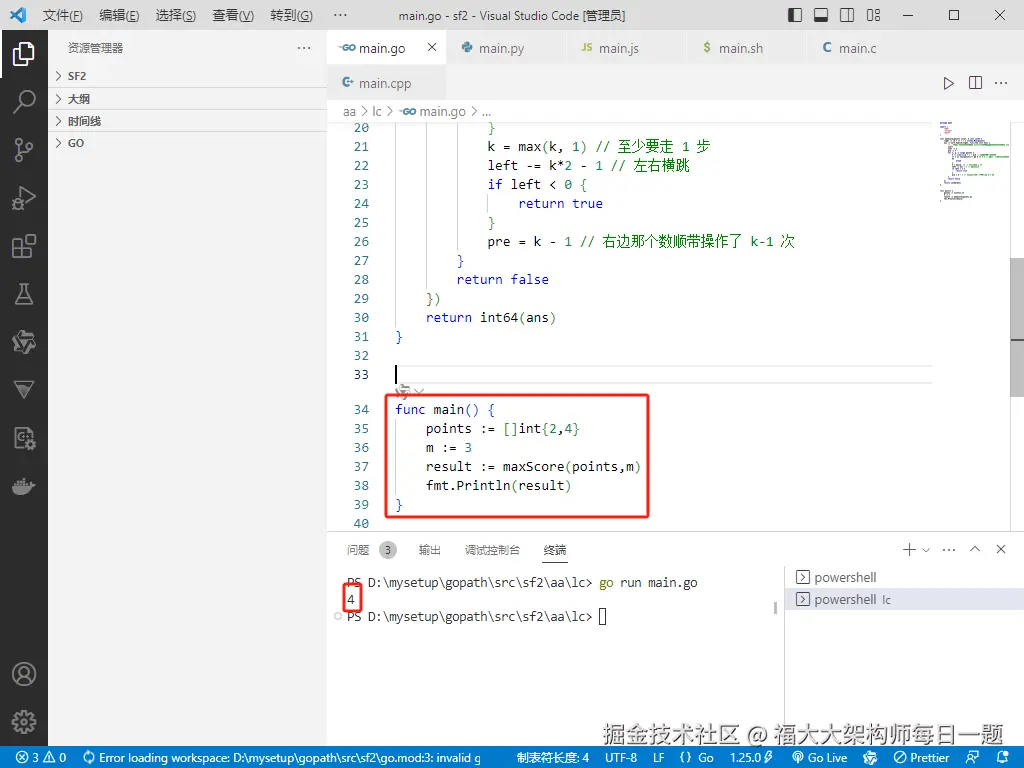
func main() {
points := []int{2,4}
m := 3
result := maxScore(points,m)
fmt.Println(result)
}
Python完整代码如下:
python
# -*-coding:utf-8-*-
def maxScore(points, m):
right = (m + 1) // 2 * min(points)
lo, hi = 0, right
while lo < hi:
mid = (lo + hi) // 2
if check(mid, points, m):
hi = mid
else:
lo = mid + 1
return lo
def check(score, points, total_steps):
target = score + 1
steps_left = total_steps
pre = 0
n = len(points)
for i, p in enumerate(points):
total_needed = (target - 1) // p + 1
k = total_needed - pre
if i == n - 1:
if k <= 0:
break
if k < 1:
k = 1
steps_left -= 2 * k - 1
if steps_left < 0:
return True
pre = k - 1
return False
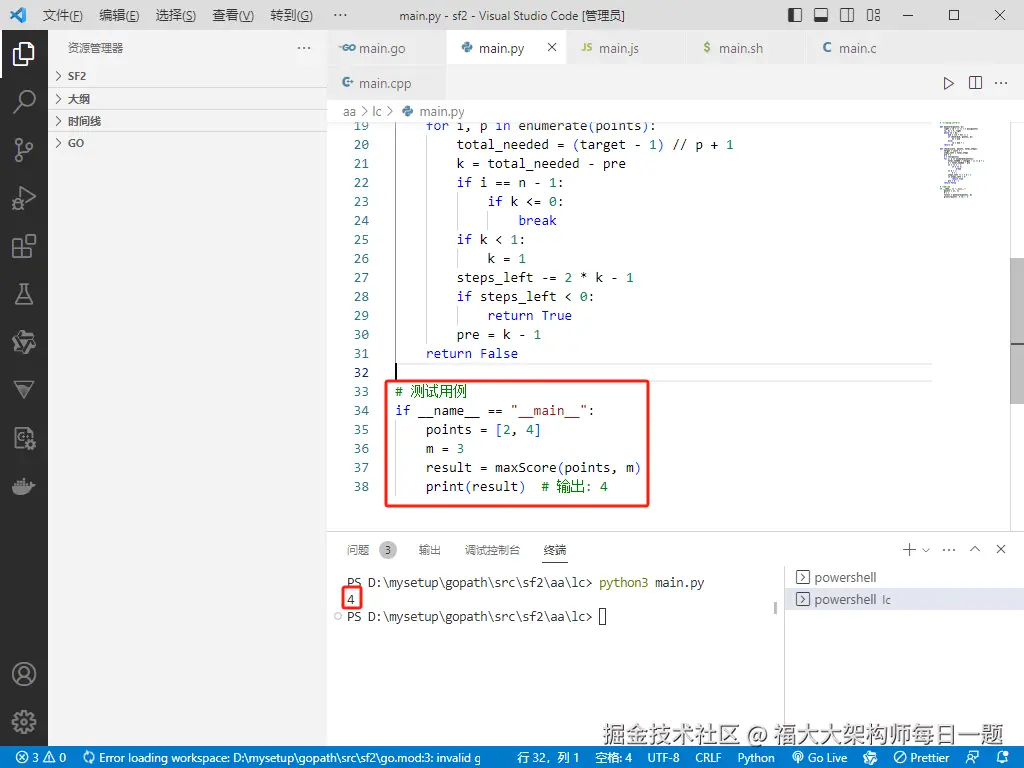
# 测试用例
if __name__ == "__main__":
points = [2, 4]
m = 3
result = maxScore(points, m)
print(result) # 输出: 4