剑指offer-23、搜索⼆叉树的后序遍历序列

题⽬描述

输⼊⼀个整数数组，判断该数组是不是某⼆叉搜索树的后序遍历的结果。如果是则返回true,否则返回false 。假设输⼊的数组的任意两个数字都互不相同。

提示：

⼆叉搜索树是指⽗亲节点⼤于左⼦树中的全部节点，但是⼩于右⼦树中的全部节点的树。
该题我们约定空树不是⼆叉搜索树
后序遍历是指按照 "左⼦树-右⼦树-根节点" 的顺序遍历
参考下⾯的⼆叉搜索树，示例 1

示例1

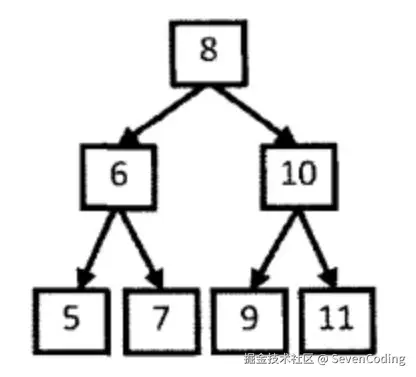
输⼊：[1,3,2] 返回值：true 说明：是上图的后序遍历，返回true

思路及解答

需要判断给定的整数数组是否是某个二叉搜索树(BST)的后序遍历结果。二叉搜索树具有以下特性：

左子树所有节点的值小于根节点的值
右子树所有节点的值大于根节点的值
左右子树也必须是二叉搜索树

后序遍历的顺序是：左子树 → 右子树 → 根节点，因此数组的最后一个元素一定是根节点

递归（标准解法）

注意是⼆叉搜索树，如果是后续遍历的话，那么应该最后⼀个元素是中间元素 mid ，前⾯的元素可以分为两部分，⼀部分⽐ mid ⼩，另⼀部分全部⽐ mid ⼤。如果破坏这个原则，那么就应该输出No 。采取分⽽治之的⽅法，分别递归检查左⼦树以及右⼦树：

确定根节点：后序遍历的最后一个元素是根节点
划分左右子树：从数组开头找到第一个大于根节点的元素，该元素之前为左子树，之后到根节点前为右子树
验证BST性质：右子树所有元素必须大于根节点
递归验证：对左右子树重复上述过程

java 复制代码

public class Solution {
    public boolean VerifySquenceOfBST(int[] postorder) {
        if (postorder == null || postorder.length == 0) {
            return false; // 空树不是BST
        }
        return verify(postorder, 0, postorder.length - 1);
    }
    
    private boolean verify(int[] postorder, int start, int end) {
        if (start >= end) {
            return true; // 单个节点总是BST
        }
        
        int root = postorder[end]; // 根节点是最后一个元素
        int i = start;
        // 找到第一个大于根节点的元素，作为左右子树分界
        while (i < end && postorder[i] < root) {
            i++;
        }
        
        // 检查右子树是否都大于根节点
        for (int j = i; j < end; j++) {
            if (postorder[j] < root) {
                return false;
            }
        }
        
        // 递归检查左右子树
        return verify(postorder, start, i - 1) && verify(postorder, i, end - 1);
    }
}

时间复杂度：O( <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 n^2 </math>n2)，n 为⼆叉树节点的个数，当树为链式时时间复杂度最坏为 O( <math xmlns="http://www.w3.org/1998/Math/MathML"> n 2 n^2 </math>n2)
空间复杂度：O(n)，当树为链式结构时，递归深度为 n

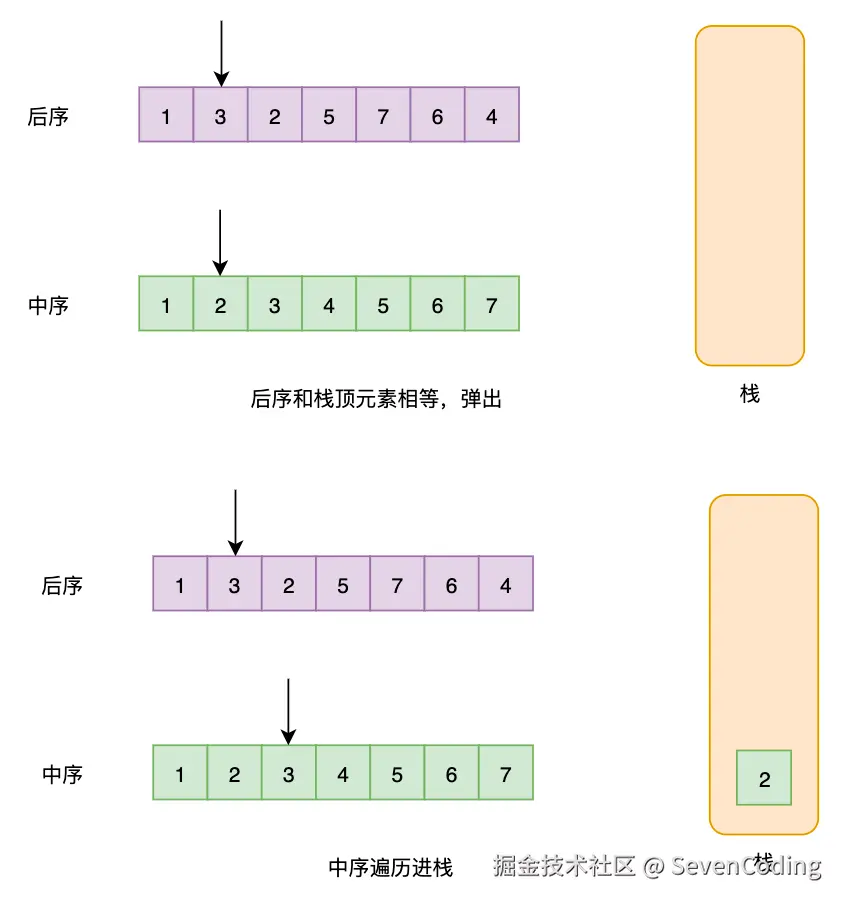
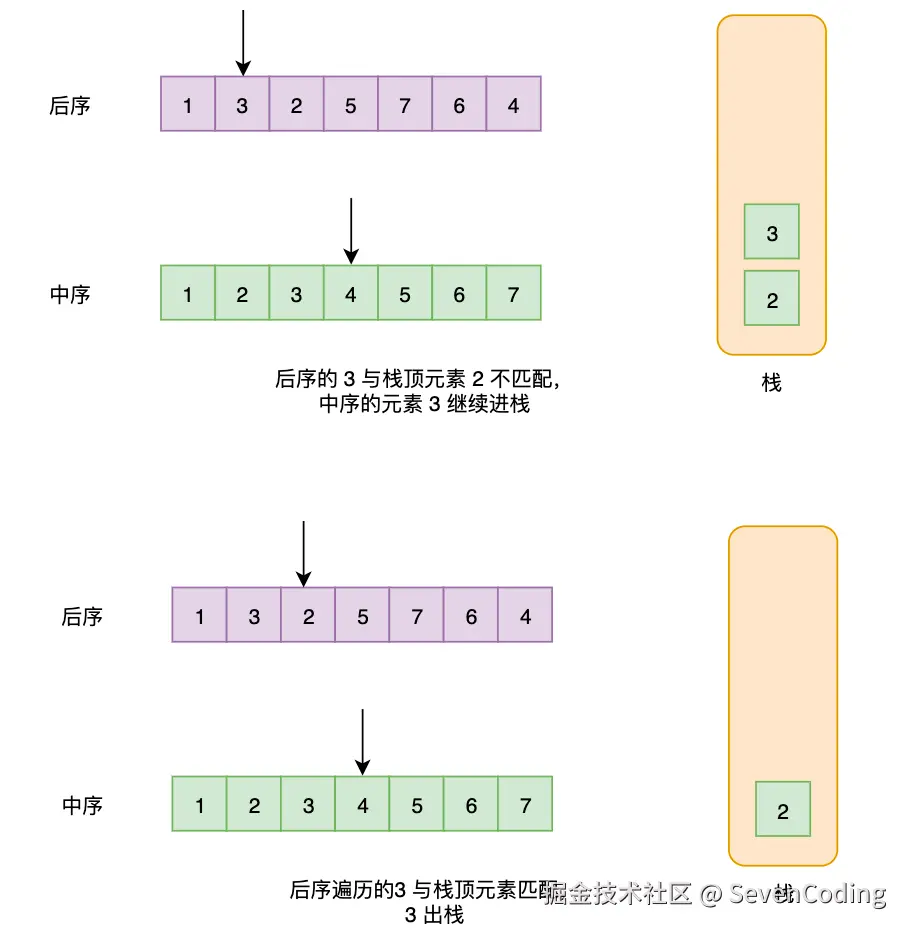
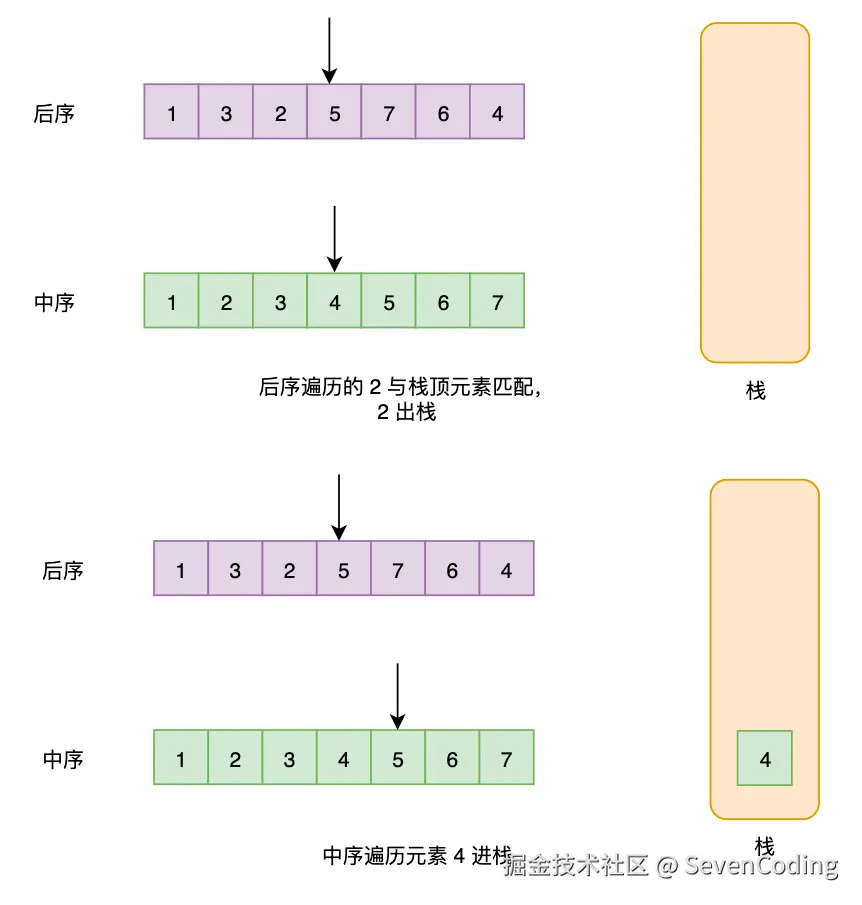
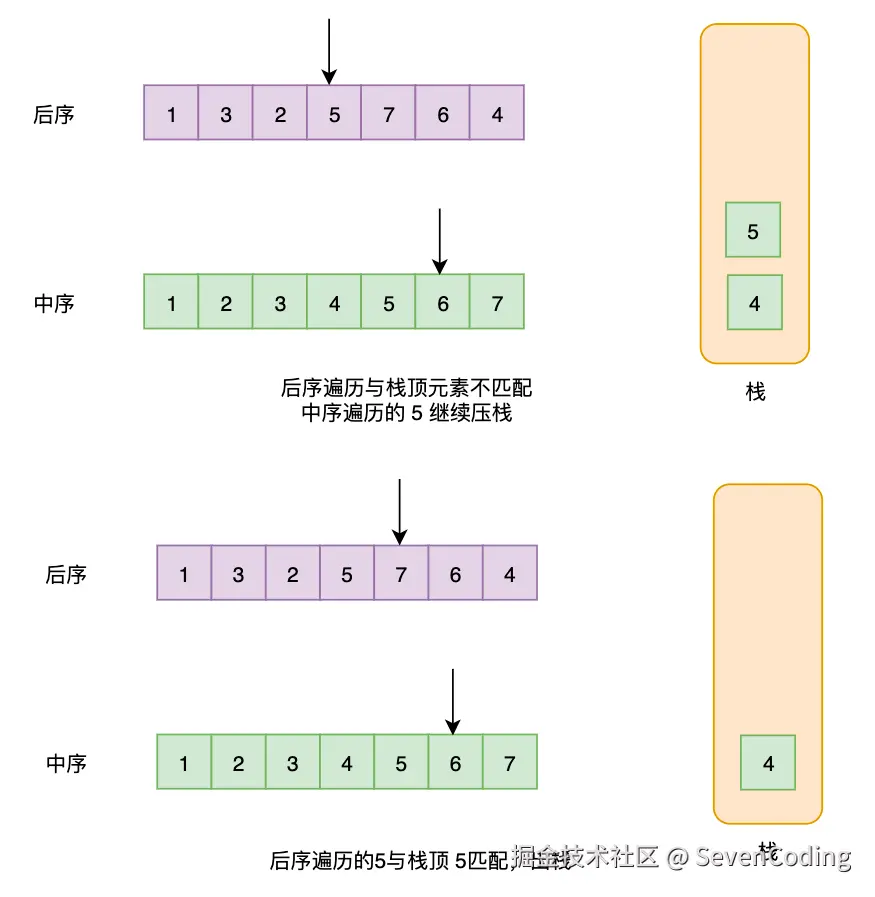
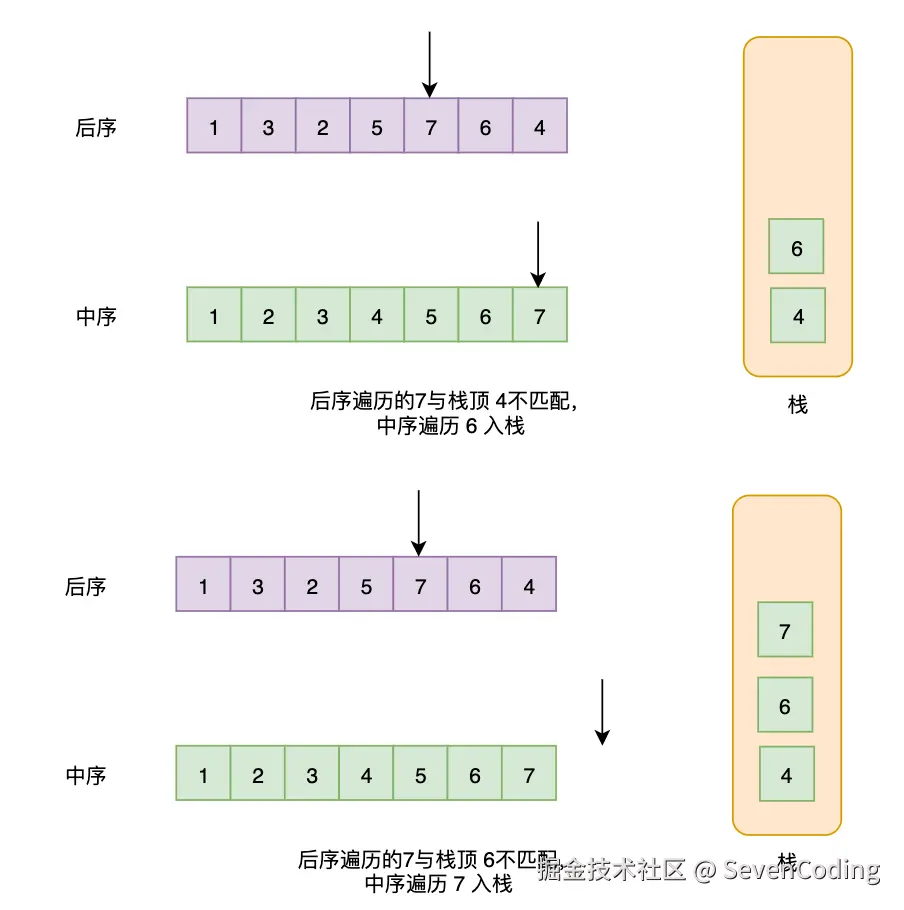
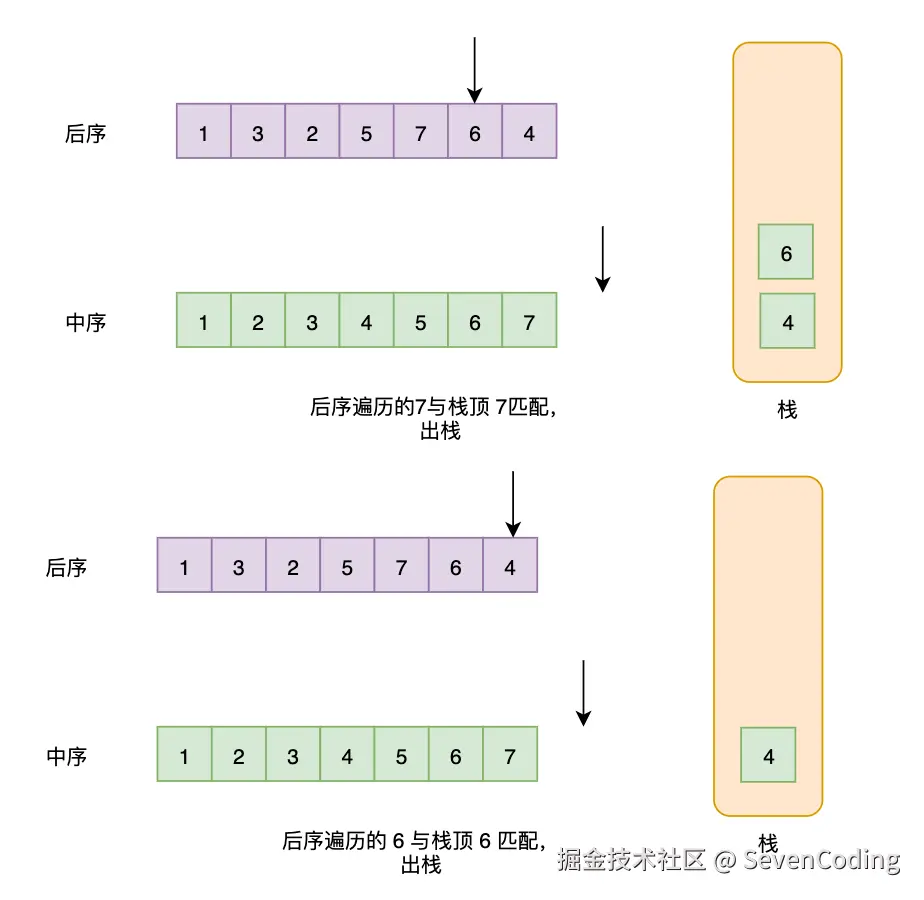
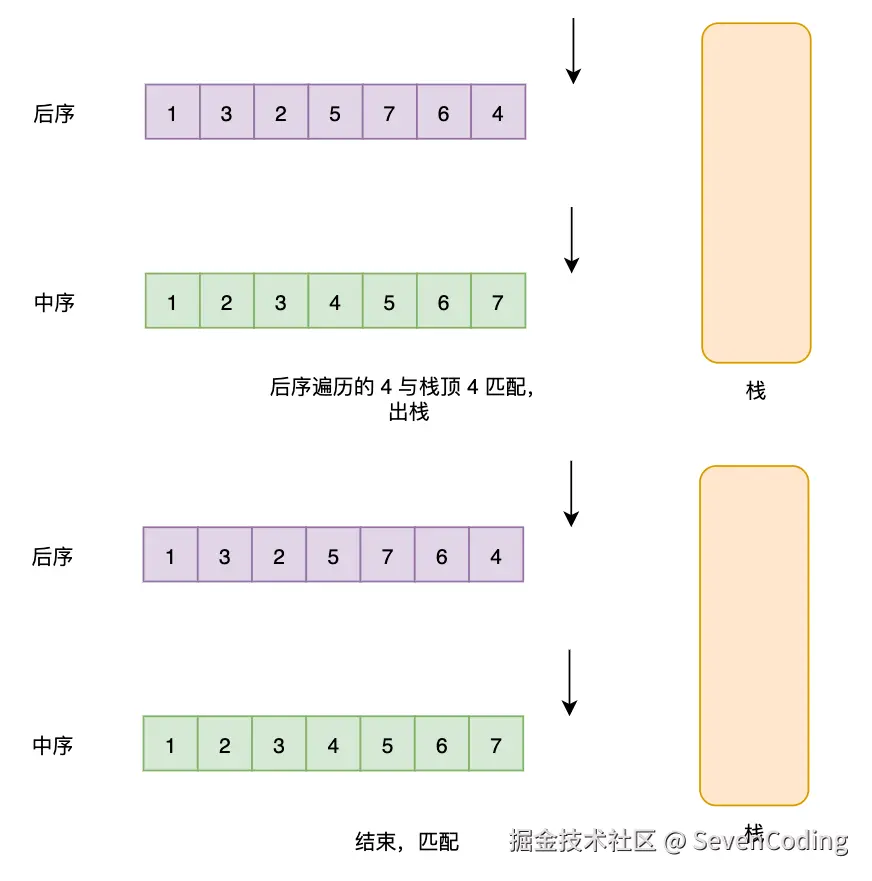
单调栈法

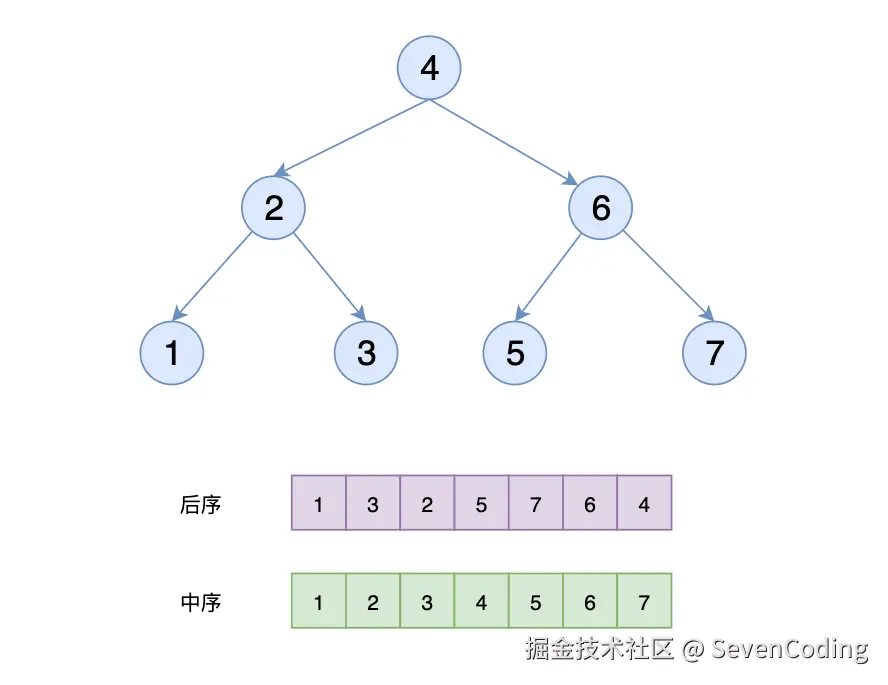
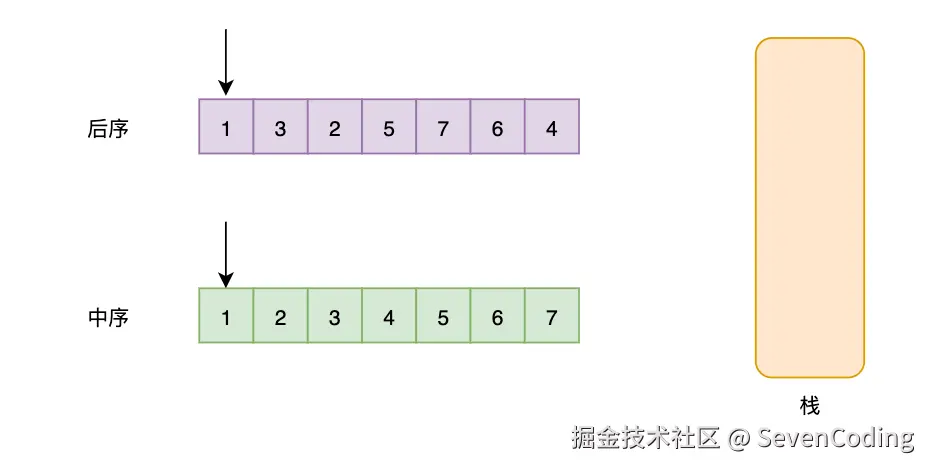
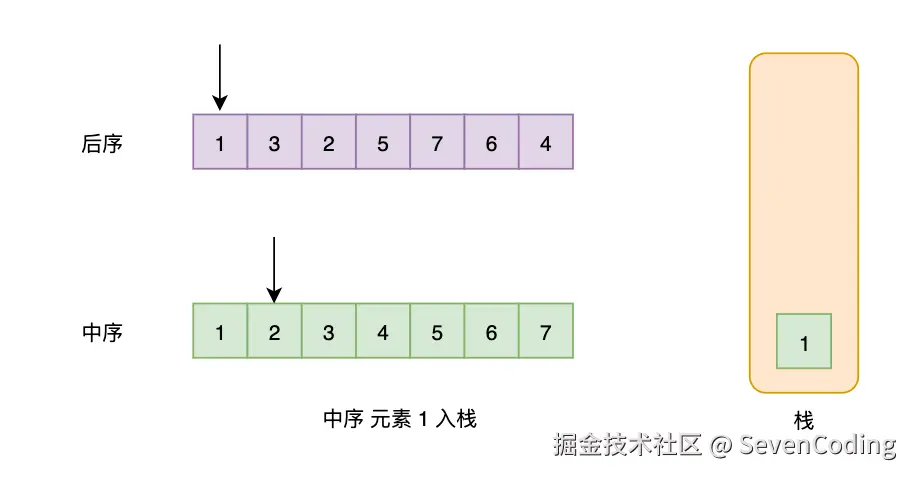
利用单调栈和后序遍历的倒序特性：

逆序处理：后序遍历的逆序是"根→右→左"，类似于变种的前序遍历
维护最小值：使用单调栈保持递增顺序，遇到较小值时弹出并更新最小值
验证性质：确保当前元素不大于最小值（即违反BST性质）

java 复制代码

public boolean verifyPostorder(int[] postorder) {
    if (postorder == null || postorder.length == 0) {
        return false;
    }
    
    Stack<Integer> stack = new Stack<>();
    int max = Integer.MAX_VALUE; // 初始化最大值
    
    // 从后往前遍历
    for (int i = postorder.length - 1; i >= 0; i--) {
        int current = postorder[i];
        // 如果当前节点大于max，违反BST性质
        if (current > max) {
            return false;
        }
        
        // 弹出所有比当前节点大的元素，并更新max
        while (!stack.isEmpty() && stack.peek() > current) {
            max = stack.pop();
        }
        
        stack.push(current);
    }
    
    return true;
}

时间复杂度：O(n)，每个元素最多入栈和出栈一次
空间复杂度：O(n)，最坏情况下需要存储所有元素