彻底搞懂 RoPE：位置编码的新范式

Transformer系列文章：

在 Transformer 架构中，位置编码（Position Encoding）是理解序列顺序的关键机制。自从 Google 提出原始的 Sinusoidal 编码以来，研究者一直在探索更高效、可泛化的方式。RoPE（Rotary Positional Embedding） 就是在这一背景下被提出的，它已被广泛应用于大模型如 LLaMA、GPT-NeoX、Grok、ChatGLM 等，是现代 LLM 架构的标准配置。

本文将深入解析 RoPE 的数学原理、实现方式、优点，以及与其他位置编码方法的对比。

所有相关源码示例、流程图、模型配置与知识库构建技巧，我也将持续更新在Github：LLMHub，欢迎关注收藏！

希望大家带着下面的问题来学习，我会在文末给出答案。

RoPE 明明是"位置编码"，为什么不直接加在 embedding 上，而是要"旋转"查询和键向量？
RoPE 如何实现相对位置建模？它是怎么让注意力知道"距离"的？
RoPE 的"旋转矩阵"会不会破坏向量的语义信息？这种操作真的合理吗？

为什么需要位置编码？

Transformer 本身不具备序列感知能力，因为它的结构是并行的、多头注意力机制，并没有天然的顺序意识。

所以必须引入某种**"位置信息"**来帮助模型区分第1个 token 和第10个 token。

传统的两种位置编码方式

1. 绝对位置编码（Absolute PE）

最早的 Sinusoidal Encoding（如在原始 Transformer 中）使用如下公式：

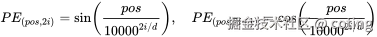
优点：无需学习，固定函数

缺点：绝对编码，无法处理变化的上下文窗口或相对关系。

2. 可学习位置向量（Learned PE）

直接给每个位置一个可学习向量 pos_embedding[position]，缺点是固定长度，不能泛化到更长序列。

RoPE 是什么？

RoPE（Rotary Position Embedding），由 Su et al. 在论文《RoFormer: Enhanced Transformer with Rotary Position Embedding》中提出，核心思想是：

"不是将位置编码与 token embedding 相加，而是通过一个旋转矩阵操作，将位置信息引入 Q、K 向量的角度中。"

用直观的话说，就是：

将位置编码看作一个二维旋转角度
让 QK 的 dot-product 计算本身隐含序列顺序差异
因为旋转可以表示相对位置，所以天然支持 相对位置感知

RoPE 的数学原理（通俗理解）

我们先看 Transformer 中注意力的核心：

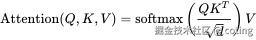
在 RoPE 中，我们不是单纯使用 Q 和 K，而是将它们进行位置旋转处理：

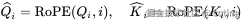
其中的旋转操作可以理解为将向量每对两个维度旋转一个角度，角度由位置 index 决定。例如在二维空间：

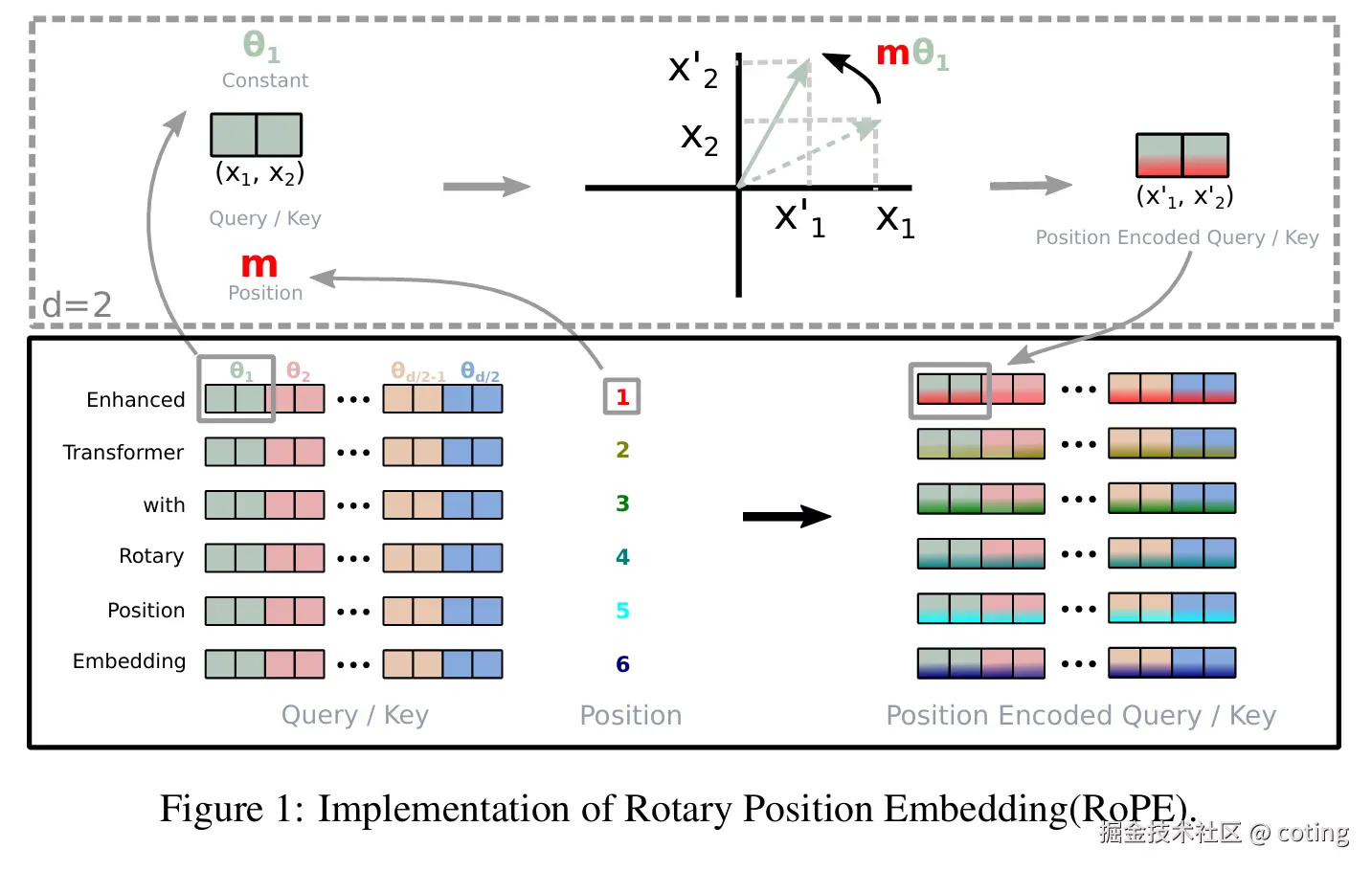
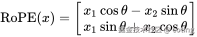
整个向量通过旋转矩阵变换，就带有了与位置相关的角度偏移。

RoPE 的 Python 实现（简化版）

python 复制代码

import torch

def apply_rope(x, seq_len, dim):
    half_dim = dim // 2
    freqs = torch.exp(-torch.arange(0, half_dim, 2) * (math.log(10000.0) / half_dim))
    angles = torch.arange(seq_len).unsqueeze(1) * freqs.unsqueeze(0)  # [seq_len, dim//2]
    
    sin = torch.sin(angles)
    cos = torch.cos(angles)

    x1, x2 = x[..., 0::2], x[..., 1::2]
    x_rotated = torch.stack([x1 * cos - x2 * sin, x1 * sin + x2 * cos], dim=-1)
    return x_rotated.flatten(-2)

这个过程在 GPT-NeoX、LLaMA 中会集成在 rotary_embedding 层中。

RoPE 的优点总结

优点	说明
支持相对位置感知	可以泛化到比训练时更长的序列（如 LLaMA3 支持 128k tokens）
高效计算	只对 Q/K 做变换，兼容现有 Attention 实现
保留周期信息	类似于 Sinusoidal 的周期性，但用旋转实现，保留了"频率"概念
泛化能力更强	比起 Learned PE 或 Absolute PE 更容易迁移到不同长度任务中

应用实例：哪些模型使用了 RoPE？

LLaMA 系列（1**~****3）**：大规模开源模型都使用 RoPE
Grok-1（xAI）：采用 RoPE + MoE 架构
GPT-NeoX：引入 RoPE 替代原始位置编码
ChatGLM 系列：国产 LLM 中广泛采用
Baichuan, InternLM, Qwen 等：国产大模型通用配置

总结

RoPE 是当前大语言模型中最实用、最主流的序列位置编码方式之一。它利用了简单的数学变换（旋转矩阵），在计算成本几乎不变的情况下，实现了对相对位置的建模能力和长序列泛化能力。

在你构建或微调 Transformer 模型时，如果需要支持：

更长的上下文窗口
更强的相对位置感知
更好的跨长度泛化能力

RoPE 是首选方案之一。

📌 延伸阅读：

原论文：RoFormer: Enhanced Transformer with Rotary Position Embedding
实现参考：LLaMA GitHub
对比位置编码：The Annotated Transformer

最后，我们回答一下文章开头提出的问题。

为什么不是加在 embedding 上，而是旋转 q/k？

因为 RoPE 的核心目的不是告诉模型"这是第几号 token"，而是告诉模型两个 token 之间的相对距离 。而注意力机制正是通过 qᵀk来判断关系的，所以将位置偏移编码直接融入q和 k 更自然且高效。加法（如原始 PE）只给了"绝对位置"，而旋转能建模"相对差值"。 2. RoPE 如何实现相对位置建模？

RoPE 的旋转操作具有数学性质：

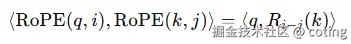
也就是说，旋转后 qᵀk 的值只与位置差值 i − j 有关，这就自然实现了相对位置建模 ------ 不关心你在哪儿，而关心你们之间相距多远。

旋转会破坏语义向量吗？

不会。RoPE 的旋转操作是一种保长（length-preserving）的线性变换（本质是二维向量在复数平面上的相位偏移），不会改变向量的模长，只会影响方向角度。在高维空间中，这种方式可以在不破坏语义结构的前提下，注入位置信息。

关于深度学习和大模型相关的知识和前沿技术更新，请关注公众号coting！

所有相关源码示例、流程图、模型配置与知识库构建技巧，我也将持续更新在Github：LLMHub，欢迎关注收藏！