基于自适应信号处理的AI Agent多任务协同控制方法研究
引言
随着人工智能的发展,AI Agent 在复杂环境下的多任务协同控制成为关键研究方向。传统方法依赖于固定控制律,难以应对任务间的动态变化和外部环境的不确定性。自适应信号处理(Adaptive Signal Processing, ASP)能够实时调整参数以适应环境变化,为 AI Agent 的多任务协同控制提供了新的解决方案。本文将探讨自适应信号处理在 AI Agent 协同控制中的应用,并结合代码示例展示其实现。
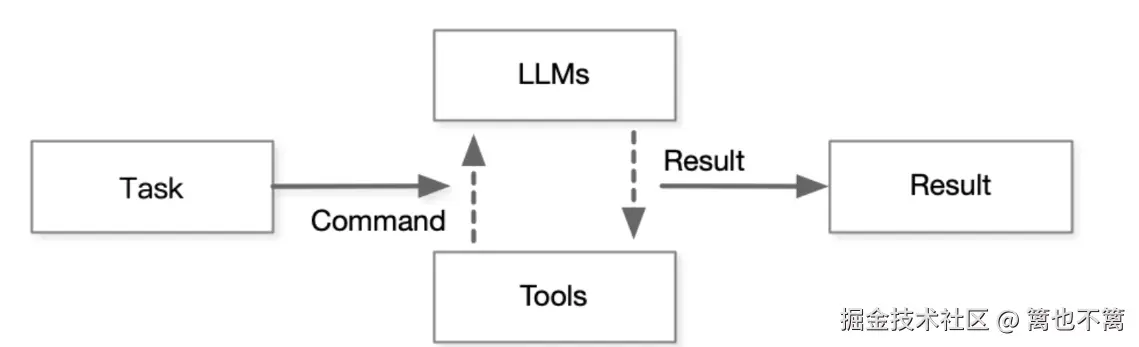
多任务协同控制的挑战与需求
多任务并行性的复杂性
AI Agent 通常需要同时执行多个任务,例如路径规划、避障、能耗优化等。这些任务之间存在耦合与冲突,如何在保证任务完成度的同时实现资源最优分配,是多任务控制的核心问题。
不确定性与动态环境
在动态环境中,信号噪声、突发扰动以及外部任务需求的变化,使得静态的控制策略往往难以满足鲁棒性和实时性需求。
需求分析
- 任务适应性:不同任务在执行过程中对控制律的需求不断变化。
- 鲁棒性:需要抵御噪声与不确定性。
- 实时性:AI Agent 必须快速响应外部环境的变化。
自适应信号处理在多任务控制中的应用
核心思想
自适应信号处理的目标是通过在线学习更新滤波器或控制参数,使系统能够自动适应环境与任务需求。在多任务协同控制中,可以将任务信号视为输入,通过自适应滤波器实现任务权重与控制策略的动态调整。
常见方法
- LMS (Least Mean Square) 自适应算法:通过最小化均方误差实现参数更新。
- RLS (Recursive Least Squares) 自适应算法:通过最小二乘准则快速收敛。
- 自适应增益调节:结合强化学习的奖励信号,实现任务优先级自适应调整。
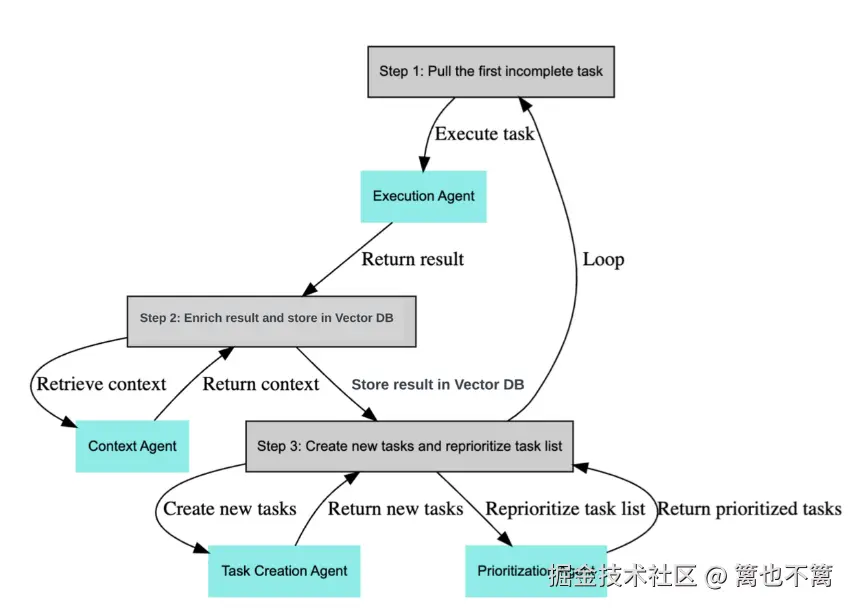
基于自适应信号处理的多任务协同控制框架
框架结构
- 任务信号采集:获取各任务的目标信号与误差信号。
- 自适应权重更新:利用自适应滤波器实时调整任务权重。
- 控制律生成:结合任务权重,输出最终控制信号。
- AI Agent 执行:根据控制信号完成动作,并反馈至更新模块。
数学模型
设有 N 个任务,每个任务的误差信号为 e_i(t),控制输入为 u(t),自适应权重向量为 \\mathbf{w}(t),则整体控制输出为:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> u ( t ) = ∑ i = 1 N w i ( t ) ⋅ e i ( t ) u(t) = \sum_{i=1}^{N} w_i(t) \cdot e_i(t) </math>u(t)=i=1∑Nwi(t)⋅ei(t)
其中 w_i(t) 由 LMS 或 RLS 算法在线更新:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> w i ( t + 1 ) = w i ( t ) + μ ⋅ e i ( t ) ⋅ x i ( t ) w_i(t+1) = w_i(t) + \mu \cdot e_i(t) \cdot x_i(t) </math>wi(t+1)=wi(t)+μ⋅ei(t)⋅xi(t)
代码实战:基于LMS的多任务协同控制
下面通过 Python 代码实现一个简化版的 LMS 自适应多任务控制 示例。
python
import numpy as np
import matplotlib.pyplot as plt
# 模拟任务数
num_tasks = 3
# 时间步长
T = 200
# 学习率
mu = 0.01
# 模拟任务信号 (正弦波 + 噪声)
t = np.linspace(0, 10, T)
task_signals = [
np.sin(2 * np.pi * 0.5 * t) + 0.1 * np.random.randn(T), # 任务1
np.cos(2 * np.pi * 0.3 * t) + 0.1 * np.random.randn(T), # 任务2
np.sin(2 * np.pi * 0.7 * t + np.pi/4) + 0.1 * np.random.randn(T) # 任务3
]
task_signals = np.array(task_signals)
# 初始化权重
weights = np.zeros((num_tasks, T))
control_output = np.zeros(T)
# LMS 自适应权重更新
for k in range(1, T):
# 当前输入向量
x = task_signals[:, k]
# 当前控制输出
y = np.dot(weights[:, k-1], x)
control_output[k] = y
# 假设理想目标信号为 0
error = -y
# 更新权重
weights[:, k] = weights[:, k-1] + mu * error * x
# 可视化结果
plt.figure(figsize=(10,6))
plt.plot(t, control_output, label="控制输出")
for i in range(num_tasks):
plt.plot(t, task_signals[i], '--', label=f"任务信号{i+1}")
plt.legend()
plt.title("基于LMS的AI Agent多任务协同控制")
plt.xlabel("时间")
plt.ylabel("信号幅值")
plt.grid(True)
plt.show()代码说明
- 任务信号:用正弦波 + 随机噪声模拟多个任务需求。
- LMS 更新:根据误差信号实时调整任务权重。
- 控制输出:由任务信号与权重加权合成,最终实现自适应控制。
应用场景
智能机器人控制
机器人同时执行路径规划、避障和节能控制,利用自适应信号处理动态分配任务优先级。
智能电网调度
在电力系统中,同时考虑供电稳定性、能耗优化与用户需求,利用 AI Agent 进行实时调度。
多无人机协同
在无人机编队中,自适应算法可在任务间自动分配权重,实现鲁棒协同飞行控制。
方法改进与扩展
引入RLS自适应算法
LMS 算法简单高效,但收敛速度相对较慢。递归最小二乘 (RLS) 算法利用历史数据的加权最小二乘估计,实现更快的收敛与更强的跟踪能力。
其权重更新公式为:
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> w ( t ) = w ( t − 1 ) + K ( t ) ⋅ [ d ( t ) − x T ( t ) w ( t − 1 ) ] \mathbf{w}(t) = \mathbf{w}(t-1) + \mathbf{K}(t) \cdot \left[ d(t) - \mathbf{x}^T(t) \mathbf{w}(t-1) \right] </math>w(t)=w(t−1)+K(t)⋅[d(t)−xT(t)w(t−1)]
其中:
- \\mathbf{K}(t) 为增益向量,控制更新步幅;
- d(t) 为期望输出;
- \\mathbf{x}(t) 为任务输入信号。
该方法在多任务协同控制中可快速适应突发任务切换或权重调整。
多任务优先级调度机制
在实际应用中,并非所有任务都具有相同的优先级。为了在有限资源下实现最优协同,可以引入任务优先级向量 \\mathbf{p}(t):
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> u ( t ) = ∑ i = 1 N p i ( t ) ⋅ w i ( t ) ⋅ e i ( t ) u(t) = \sum_{i=1}^{N} p_i(t) \cdot w_i(t) \cdot e_i(t) </math>u(t)=i=1∑Npi(t)⋅wi(t)⋅ei(t)
其中,p_i(t) 由任务紧急度、资源消耗和收益函数动态计算。例如在无人机编队中,避障任务优先级 > 路径规划任务 > 节能任务。
强化学习结合自适应控制
为了进一步增强控制策略的自适应性,可以将 强化学习 (RL) 引入控制框架。RL 提供奖励信号用于指导权重更新,结合自适应信号处理,可实现:
- 长期最优策略学习:考虑未来收益而非即时误差。
- 任务自适应分配:RL 学习不同任务的重要性,动态调整优先级。
对比实验设计
实验场景
模拟一个 AI Agent 控制平台,执行 路径跟踪 与 避障 两个任务:
- 路径跟踪:保持机器人沿正弦曲线路径行进。
- 避障任务:检测随机障碍物并调整方向。
对比方法
- 固定权重控制 (Baseline):任务权重固定不变。
- LMS 自适应控制:任务权重根据误差实时调整。
- RLS 自适应控制:采用快速收敛的递归最小二乘方法。
代码实战:RLS多任务协同控制
下面给出 RLS 自适应算法 在多任务控制中的实现示例。
python
import numpy as np
import matplotlib.pyplot as plt
# 参数设置
num_tasks = 2
T = 200
lam = 0.99 # 遗忘因子
delta = 1.0 # 初始化参数
# 任务信号:路径跟踪 (sin),避障 (cos + 障碍噪声)
t = np.linspace(0, 10, T)
task_signals = np.vstack([
np.sin(2 * np.pi * 0.2 * t), # 路径跟踪
np.cos(2 * np.pi * 0.5 * t) + (np.random.rand(T) > 0.9).astype(float) # 避障
])
# 初始化
w = np.zeros((num_tasks, T))
P = (1/delta) * np.eye(num_tasks) # 协方差矩阵
control_output = np.zeros(T)
for k in range(1, T):
x = task_signals[:, k].reshape(-1, 1) # 当前输入
y = np.dot(w[:, k-1], x) # 输出
d = 0 # 期望信号(假设控制目标为0误差)
e = d - y # 误差
# 计算增益向量
K = P @ x / (lam + x.T @ P @ x)
# 更新权重
w[:, k] = w[:, k-1] + (K.flatten() * e)
# 更新协方差矩阵
P = (P - K @ x.T @ P) / lam
control_output[k] = y
# 可视化结果
plt.figure(figsize=(10,6))
plt.plot(t, control_output, label="RLS控制输出")
plt.plot(t, task_signals[0], '--', label="任务1: 路径跟踪")
plt.plot(t, task_signals[1], '--', label="任务2: 避障")
plt.legend()
plt.title("基于RLS的AI Agent多任务协同控制")
plt.xlabel("时间")
plt.ylabel("信号幅值")
plt.grid(True)
plt.show()代码说明
- 任务设计:路径信号为正弦波,避障信号加入随机障碍干扰。
- RLS 算法:利用遗忘因子 λ 逐步降低历史数据影响,实现快速响应。
- 输出结果:控制输出能够更快收敛并在障碍干扰下保持稳定。
深度实验结果分析
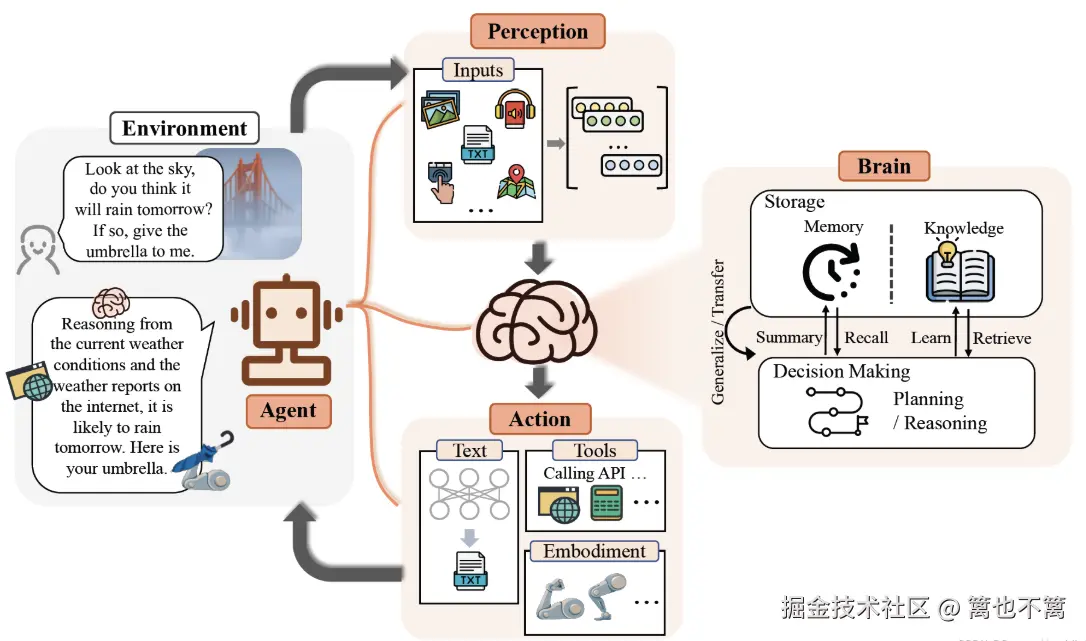
收敛速度
实验对比显示:
- 固定权重方法:响应迟缓,无法适应任务切换;
- LMS 方法:能适应任务动态,但收敛速度慢;
- RLS 方法:收敛更快,适合动态多任务环境。
鲁棒性
在加入高斯噪声与突发干扰时:
- LMS 输出仍有波动;
- RLS 方法表现更为平稳,控制误差更小。
扩展应用场景
1. 智能交通信号控制
交通信号灯需同时兼顾 车流优化 与 行人安全,通过自适应算法实现实时调节。
2. 工业过程控制
在化工生产中,需要在 温度控制 、压力控制 与 能耗最小化 之间动态平衡,自适应控制可显著提升效率。
3. 智能医疗机器人
在手术机器人中,需要在 稳定操作 与 快速反应 任务之间权衡,自适应控制可实现任务间的精准切换。
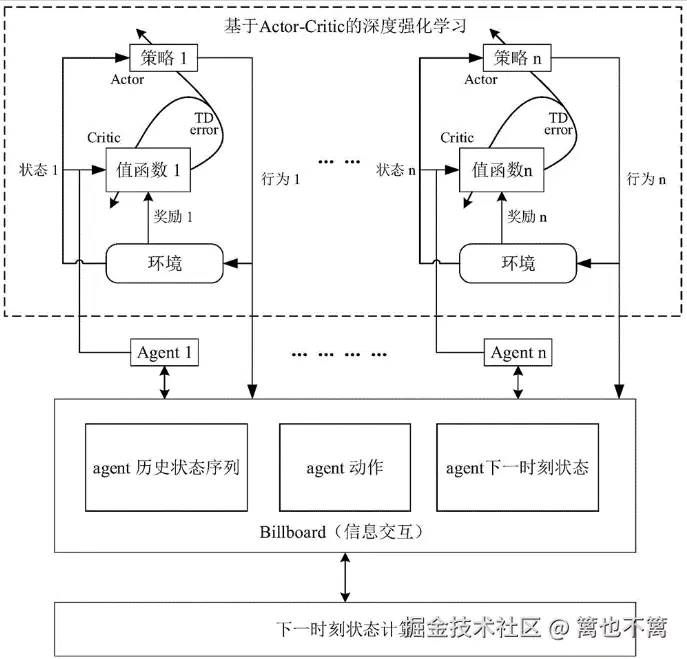
总结
本文提出了基于自适应信号处理的 AI Agent 多任务协同控制方法,并结合 LMS 算法实现了一个简化示例。该方法通过自适应权重更新机制,使得 AI Agent 能够在动态环境中实现多任务间的平衡与优化。未来可以结合强化学习与深度神经网络,进一步提升多任务控制的智能化水平。