支持向量机

一、基本概念

1、简单了解

支持向量机是一种功能强大且用途广泛的机器学习模型，能够只从线性或非线性分类、回归甚至异常检测。

SVM在中小型非线性数据集（即成百上千个实例）中大放异彩，尤其适用于分类任务。然而，它们不能很好地扩展到非常大的数据集

2、核心思想：

SVM的核心思想是找到一个最优的决策边界(超平面)，使得不同类别之间的间隔(margin)最大化。

3、关键术语

支持向量：距离决策边界最近的样本点，决定了边界的位置

超平面：在N维空间中N-1维子空间，用于分割数据，也就是决策边界

间隔：决策边界到最近支持向量的距离，SVM的目标就是找到一个超平面使得两类数据之间的间隔最大

间隔边界：超平面平移的结果，间隔最大也就是说间隔边界距离超平面最远。两个间隔边界中间的部分可以称作"街道"

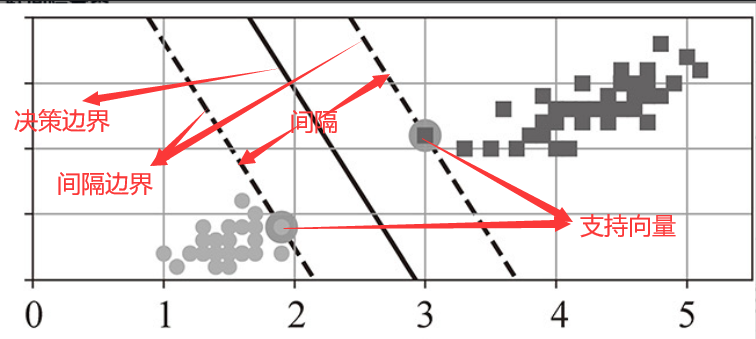
二、线性SVM分类（大间隔分类，SVC大多数样本落在决策边界外）

1、SVM训练的注意事项

SVM训练后，在"街道以外"的地方增加更多训练实例根本不会对决策边界产生影响，也就是说，它完全由位于街道边缘的实例所决定（或支持）

支持向量对特征缩放敏感：

例如：特征1（水平轴）取值范围 [0, 10]；特征2（垂直轴）取值范围 [0, 10000]（这两个特征的数值尺度（垂直刻度 vs 水平刻度）差异极大。从而导致乘积 仍可能主导决策函数 ，的作用微乎其微，如下左图所示：

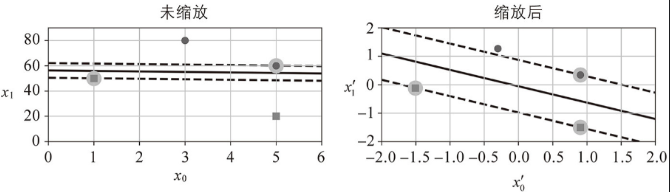
而进行特征缩放后的特征1和特征2都能够很好的发挥作用，如上右图所示。

2、硬间隔分类与软间隔分类

如果严格的让所有实例都在街道以外，并且所有训练样本必须都被超平面正确分类，这就是硬间隔分类 。其数学形式的问题为： 满足

硬间隔分类的问题：只有数据是线性可分离的时候才有效；对异常值很敏感。如下左图找不到硬间隔；右图最终显示的间隔很小，无法很好的泛化。

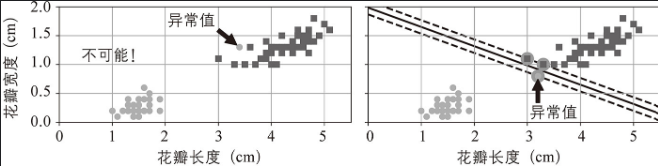
为了避免这些问题，需要使用灵活的模型，也就是允许出现部分实例出现在错误的位置（限制间隔违例）。而这种保持街道尽可能宽阔和限制间隔违例之间找到良好的平衡，就是软间隔分类。

其数学形式为： 使得

软间隔分类是在原始的决策边界描述中加入松弛变量，通过C惩罚松弛变量，从而控制分类的严格性

3、分类的工作原理

计算决策函数------ 训练 ------ 预测

• 计算决策函数： 来预测新实例x的类别，其中b是偏置特征，始终为1。如果结果是正数表示阳性类1，否则为阴性类0。
• 训练：找到权重w和偏置b，使得间隔尽可能的大 ------> 街道边界为决策函数为-1/1的地方，想要街道尽可能的变宽
  • 硬间隔：间隔 最大→ ||w||最小 → 最小（这里使用L2范式是因为能够在w=0的时候可导）→ 最小 ）
  • 软间隔约束优化：间隔 最大，分类错误的第i个样本的误差最小→ ||w|| 最小，最小 → 最小（这里使用L2范式是因为能够在w=0的时候可导）→ 最小 ）
  • 软间隔的无约束优化：根据梯度下降来寻找最小化hinge损失或平方hinge损失。间隔 最大，分类错误的第i个样本的误差最小 ------> ||w|| 最小，且满足条件：（由 推导得到）和 ------> 最小（这里使用L2范式是因为能够在w=0的时候可导）； ------ > 最小 ）

限制落在间隔内的实例数量，以及分类错误的数量（间隔内+间隔外）------> 对于硬间隔来说：阳性类>=1，阴性类<= -1

4、代码实现

默认情况，LinearSVC使用平方hinge损失，而SGDClassifier使用hinge损失。这两个类都允许通过超参数hinge或squared_hinge来选择损失。

from sklearn.datasets import make_moons
from sklearn.preprocessing import PolynomialFeatures
X, y = make_moons(n_samples=100, noise=0.15, random_state=42)  

polynomial_svm_clf = make_pipeline(
    PolynomialFeatures(degree=3),
    StandardScaler(),
    LinearSVC(C=10, max_iter=10000,random_state=42, dual=True))

# polynomial_svm_clf = make_pipeline(
#     PolynomialFeatures(degree=3),
#     StandardScaler(),
#     SVC(kernel="linear" ,C=10, max_iter=10000,random_state=42))

polynomial_svm_clf.fit(X, y)

两个流水线的最后的结果一样，一个是使用LinearSVC类，一个是使用SVC类中的linear核。

三、非线性SVM分类（SVC）

有很多数据集远不是线性可分离的，这时线性分类就不能很好的发挥作用，需要引入非线性分类。

当SVM处理非线性问题的时候，他是通过核函数将数据映射到高维空间，在高维空间中寻找线性分类超平面。核技巧就是无需显式的计算高维映射，直接通过核函数在原始空间中计算高维空间的内积，节省计算成本。

1、多项式核（ploy）

显式的添加多项式特征实现起来很简单，但问题是多项式太低阶，处理不了非常复杂的数据，而高阶则会创造出大量的特征导致模型训练太慢。而SVM中的多项式核能够很好的解决这个问题。

数学形式： ，

d（degree）：多项式阶数，控制非线性强度。d=1 时退化为线性核。d 越大，模型越复杂（可能过拟合）。

γ（gamma） ：缩放系数，默认为 。控制内积对核值的影响。

r（coef0）：偏置项，默认为 0。调整低阶多项式项的权重。

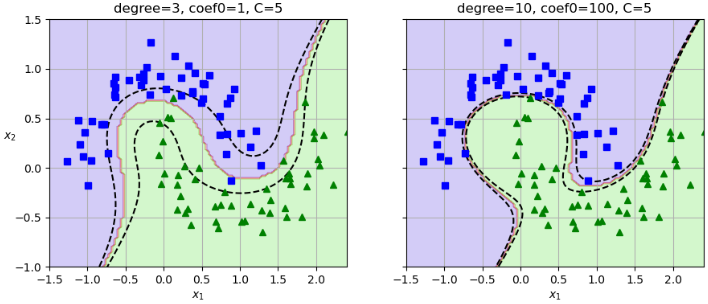
2、相似性特征（rbf）

相似函数可以测量每个实例与一个特定地标之间的相似性程度，接下来采用高斯径向基函数作为相似函数（这个一个从0（与地标距离非常远）到1（地标）变化的钟形函数）。选择"地标"最简单的方法是在数据集里每一个实例的位置上创建一个地标。这会创造出许多维度，因而也增加了转换后的训练集线性可分离的机会。缺点是，一个有m个实例n个特征的训练集会被转换成一个有m个实例m个特征的训练集（假设抛弃了原始特征）。如果训练集非常大，那就会得到同样大数量的特征。

数学形式：

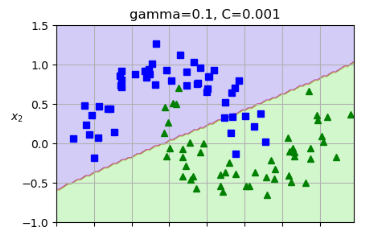
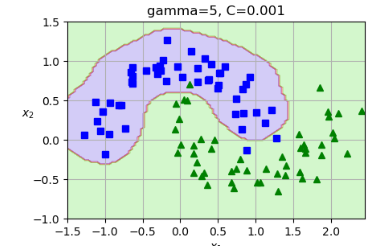
γ（gamma） ：控制高斯函数的宽度（即单个样本的影响范围）。γ 越大，决策边界越复杂（过拟合风险）；γ 越小，边界越平滑（可能欠拟合）；默认值为 。

3、sigmoid核

模仿神经网络的双曲正切激活函数，但是这个核性能不稳定。

数学形式： ，

γ（gamma）：缩放系数，类似 RBF 核；

r（coef0）：偏置项，控制函数平移。

4、计算复杂度

类	时间复杂度	核外支持	是否需要缩放	核技巧
LinearSVC		否	是	否
SVC		否	是	是
SGDClassifier		是	是	否

四、SVM回归（SVR让大多数样本落在决策边界内）

使用SVM做回归的技巧是调整目标：SVM回归不是试图在两个类之间拟合最大可能的街道同时限制间隔违例，而是在街道上极可能拟合多的实例，同时限制间隔违例（即街道之外的实例），街道的宽度由超参数epsilon控制。

减小epsilon会增加支持向量的数量，从而使模型得到正则化。 此外，如果在间隔区域内添加更多的训练实例，它不会影响模型的预测。因此，该模型被称为 不敏感。

svm_poly_reg = make_pipeline(StandardScaler(),
                             SVR(kernel="poly", degree=2, C=0.01, epsilon=0.1))
svm_poly_reg.fit(X, y)
svm_poly_reg2 = make_pipeline(StandardScaler(),
                             SVR(kernel="poly", degree=2, C=100, epsilon=0.25))
svm_poly_reg2.fit(X, y)

svm_poly_reg._support = find_support_vectors(svm_poly_reg, X, y)
svm_poly_reg2._support = find_support_vectors(svm_poly_reg2, X, y)

fig, axes = plt.subplots(ncols=2, figsize=(9, 4), sharey=True)
plt.sca(axes[0])
plot_svm_regression(svm_poly_reg, X, y, [-1, 1, 0, 1])
plt.title(f"degree={svm_poly_reg[-1].degree}, "
          f"C={svm_poly_reg[-1].C}, "
          f"epsilon={svm_poly_reg[-1].epsilon}")
plt.ylabel("$y$", rotation=0)
plt.grid()

plt.sca(axes[1])
plot_svm_regression(svm_poly_reg2, X, y, [-1, 1, 0, 1])
plt.title(f"degree={svm_poly_reg2[-1].degree}, "
          f"C={svm_poly_reg2[-1].C}, "
          f"epsilon={svm_poly_reg2[-1].epsilon}")
plt.grid()
plt.show()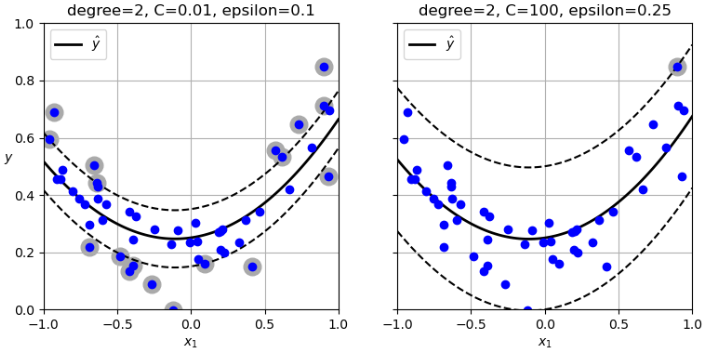

五、对偶问题

对偶问题（Dual Problem）是数学优化中的一个重要概念，特别是在线性规划和非线性规划中。简单来说，每一个优化问题（称为原始问题，Primal Problem）都有一个与之对应的对偶问题。对偶问题提供了从另一个角度理解和解决原始问题的方法。

通常情况下，对偶问题的解只能算是原始问题的解的下线限，但是在某些情况下，他可能跟原始问题的解完全相同。SVM的优化问题刚好属于某些情况（对偶问题的解和原始的解完全相同），所以可以选择解决原始问题还是对偶问题。

用拉格朗日乘子法将主问题转化为对偶问题：

拉格朗日函数：，这里的 是拉格朗日乘子向量

转化后： , 且

一旦得到最小化该等式（使用二次规划求解器）的向量 ，就可以使用下面公式 来计算最小化原始问题的 和 。在这个公式中， 表示支持向量的数量，也就是非0 a(i)的数量。

当训练实例的数量小于特征数量时，解决对偶问题比原始问题更快速。更重要的是，对偶问题能够实现核技巧，而原始问题不可能实现。

六、把SVM 看成梯度下降来实现

对于线性SVM来说，损失函数可以写成：

第一项：hinge loss ，只在"没被正确分类/分到了间隔内"时才有损失

第二项：L2正则化，

写成梯度下降版本（平均化+hinge loss）为：

由损失函数可以看出：

C增大 → 正则化系数 减小 → 更重视分类误差（拟合能力上升，偏差下降，方差上升）

C减小 → 正则化系数增大 → 更重视间距（泛化能力上升，偏差上升，方差下降）