目录
[1. 按照二叉搜索树的方式插入新节点](#1. 按照二叉搜索树的方式插入新节点)
[2. 按需变色或旋转+变色](#2. 按需变色或旋转+变色)
[(1)uncle 存在且为红](#(1)uncle 存在且为红)
[(2)uncle 不存在](#(2)uncle 不存在)
部分红黑树图画来自维基百科!!
1.红黑树的概念及规则
红黑树是一种自平衡的二叉搜索树
通过特定规则和旋转 操作确保最长路径的节点数不超过最短路径的两倍,因而是接近平衡的
通过以下规则维护近似平衡
1.每个节点非红即黑,根节点和叶子节点(NIL)为黑
这里说的叶子节点、NIL节点就是空节点
2.红色节点的子节点必须为黑
即任意路径上无连续红节点
3.从任意节点到其所有叶子节点的路径上,黑色节点数量相同
简称黑高一致
这些规则保证了最长路径(即红黑交替)的节点数不超过最短路径(即全黑)的两倍
下图为一棵合法的红黑树:
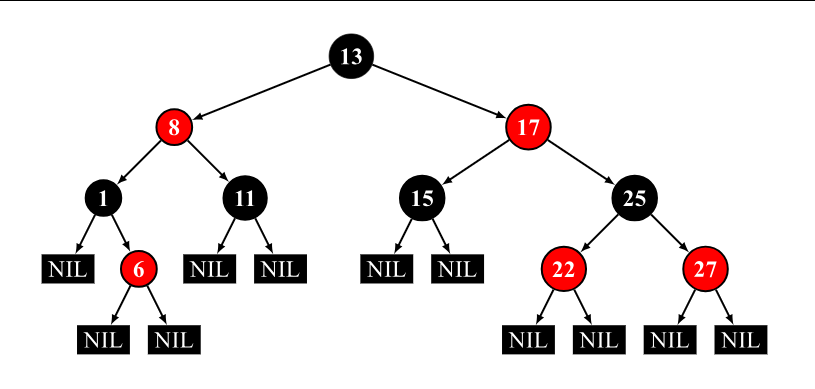
2.AVL树与红黑树的性能对比
N个数据存储在AVL树与红黑树中:
(1)AVL树高约为 1.44 logN,红黑树高约为 2 logN(上界) (我查询的数据,我也不会推导^_^) 高度差异对性能影响有限(如10亿数据时,AVL树约43层,红黑树约60层,CPU缓存可高效处理)
(2)关键区别:AVL树的苛刻平衡条件导致插入/删除时需大量旋转(最多O(logN)次),而红黑树仅需固定次数的旋转(最多2~3次)。
因此,红黑树 在动态操作上效率更高,综合性能更优 (可评10分),AVL树在查找密集型场景中略优(9.5分)
两者查找时间复杂度均为 O(logN),实际差异可忽略。
3红黑树节点定义
使用 KV 模型, 此概念可参考 前期博客 二叉搜索树的应用
enum Color
{
RED,
BLACK
};
template<class K, class V>
struct RBTreeNode
{
RBTreeNode<K, V>* _left;
RBTreeNode<K, V>* _right;
RBTreeNode<K, V>* _parent;
pair<K, V> _kv;
Color _col;
RBTreeNode(const pair<K, V>& kv)
:_left(nullptr),_right(nullptr),_parent(nullptr)
,_kv(kv),_col(RED)
{ }
};(1)节点非黑即红,使用枚举列举两种颜色
RBTreeNode类负责树节点的定义及初始化:
(1)使用模板,以适应不同数据类型
(2)struct定义,将节点暴露方便后续使用
(3这里使用三叉链,即一个节点既保存其左右孩子节点指针又保存其父亲节点指针
(4)节点中再保存存储数据的 _kv 及 颜色表示 _col
4.红黑树的插入
红黑树是特殊的二叉搜索树,红黑树的插入就是在二叉搜索树插入的基础上通过判断节点颜色的互斥性 ,进而按需变色或旋转,最终达到近似平衡的过程
那么AVL树的插入过程可以分为两步:
1. 按照二叉搜索树的方式插入新节点
template<class K, class V>
class RBTree
{
typedef RBTreeNode<K, V> Node;
public:
bool Insert(const pair<K, V>& kv)
{
if (!_root)
{
_root = new Node(kv);
_root->_col = BLACK;
return true;
}
Node* parent = _root;
Node* cur = _root;
while (cur)
{
if (kv.first > cur->_kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (kv.first < cur->_kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_parent = parent;
if (kv.first > parent->_kv.first)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
//控制红黑节点
//...
//插入结束即是成功
return true;
}
private:
//可以偷懒在这初始化
Node* _root = nullptr;
};前半截插入过程与二叉搜索树一致:
向左向右走,遇到空就开始插入,遇到相同值的就返回false(去重效果)
三叉链!!注意链接父亲节点
值得说明的是,这里默认插入节点是红色节点,这是因为如果插入黑色节点,需要调整每条路径上黑色节点的数量,
上图就有11条路经,此操作不禁令人望而却步
如果插入红色节点,情况就会好很多----
2. 按需变色或旋转+变色
注意四个节点:
cur :当前节点 parent:当前节点的父亲节点
grandfather :当前节点的父亲节点的父亲节点 uncle:当前节点的父亲节点的兄弟节点
后续画图使用 c 、p、g、u 来表示这四个节点
(1)parent不存在
cur 就是根节点,因为默认节点为红色,此时需要修正
if (!_root) { _root = new Node(kv); //修正 _root->_col = BLACK; return true; }
(2)parent存在且为黑
cur 为红色,红黑相间,不违背红黑树的规则,此时不作其余操作
(3)parent存在且为红
cur 所在路径下存在连续的红色节点,开始修正----
cur为红色,parent为红色,grandfather一定存在且为黑,因为
如果grandfather不存在,则说明在插入cur之前,树结构就出问题了(根节点不为黑色)
如果grandfather存在且为红,则说明在插入cur之前,树结构就出问题了(连续的红色节点)
此时讨论的重点转移到了 uncle 上
(1)uncle 存在且为红
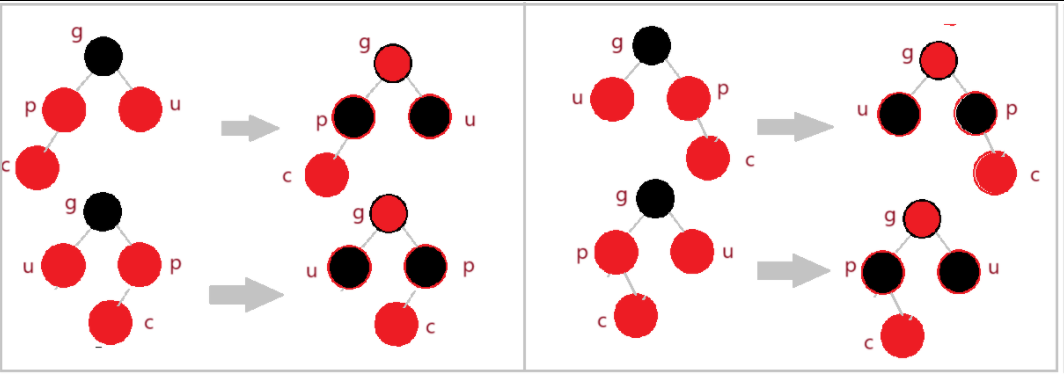
只要cur为红色,parent为红色,grandefather(此时一定)为黑色,uncle为红色
不管cur在parent的左还是右,parent在grandfather的左还是右
统一的处理方法是:将parent、uncle变黑,grandfather变红,再继续向上处理
grandfather 原来是黑色节点,此操作后变红,为了防止路径上出现连续的红节点,还需要继续向上处理 :cur = grandfather;parent = cur->_parent
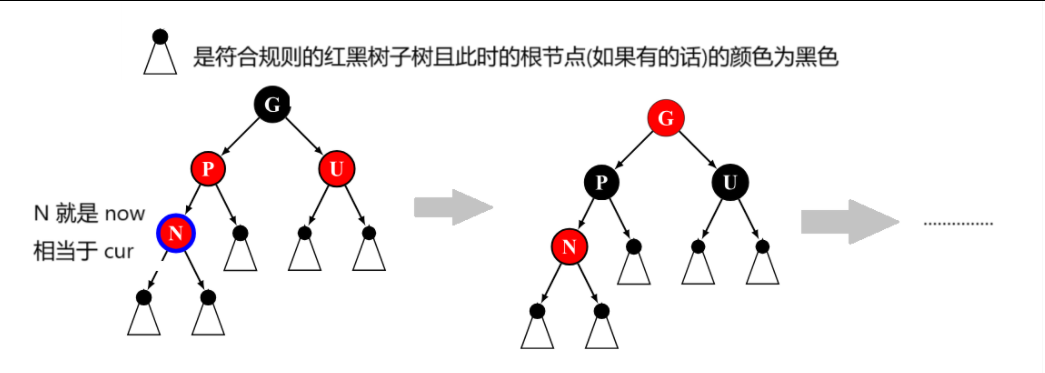
认准 cur为红色,parent为红色,grandefather为黑色,uncle为红色****的唯一标识!
(2)uncle 不存在
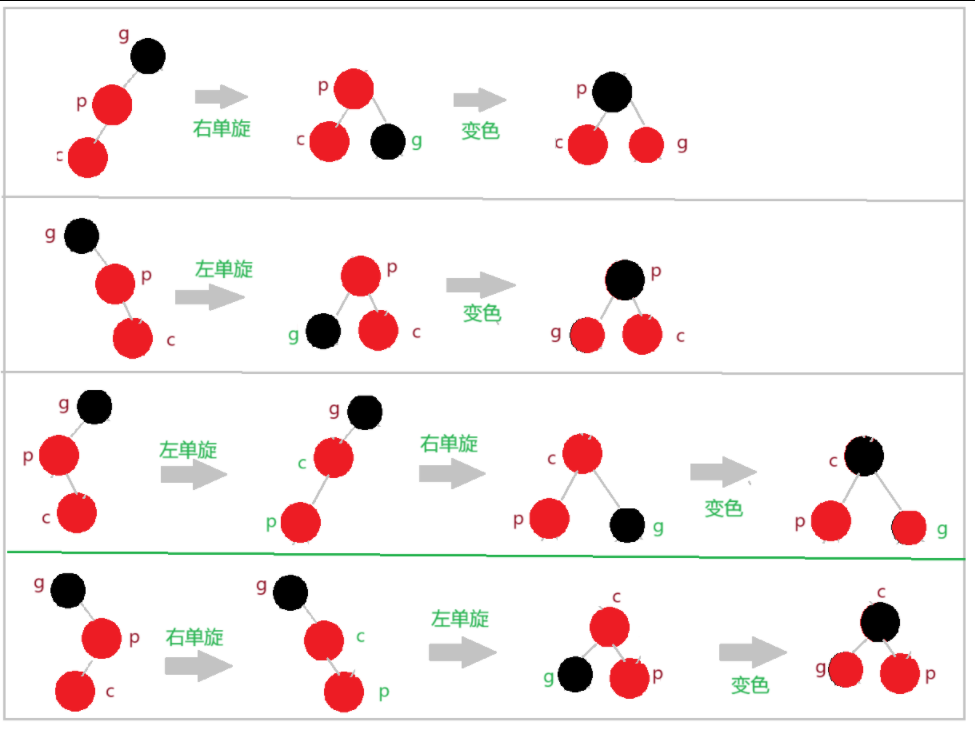
实现技巧只能是画图分析,不懂旋转的朋友参考 我的博客 AVL树的简介与部分实现
uncle不存在,cur只能是新插入的节点 ,此时的解决方法是
根据cur在parent的左还是右,parent在grandfather的左还是右,按需旋转变色
cur在parent的左 ,parent在grandfather的左:右单旋,parent变黑,grandfather变红
cur在parent的右 ,parent在grandfather的右:左单旋,parent变黑,grandfather变红
cur在parent的左 ,parent在grandfather的右:左右双旋,cur变黑,grandfather变红
cur在parent的右 ,parent在grandfather的左:右左双旋,cur变黑,grandfather变红
旋转完成以后,规则2、3没有被违反,插入结束
(3)uncle存在且为黑
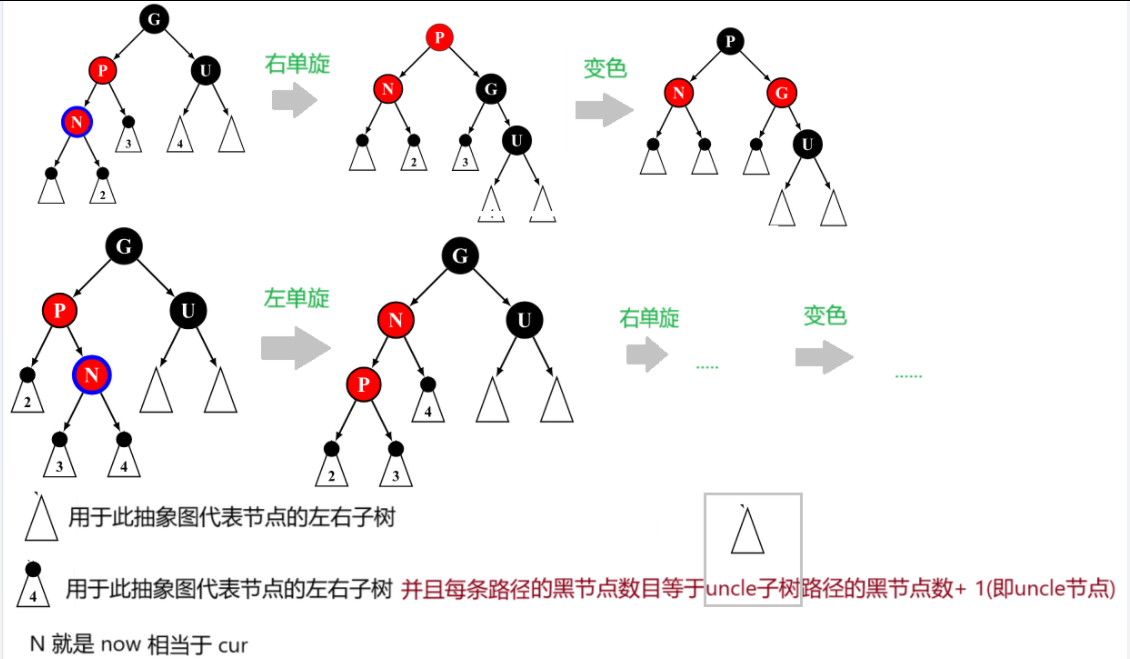
cur一定是变色上来的节点,否则就违反了规则3,
此时的解决方法与uncle不存在的解决方法一致
cur在parent的左 ,parent在grandfather的左:右单旋,parent变黑,grandfather变红
cur在parent的右 ,parent在grandfather的右:左单旋,parent变黑,grandfather变红
cur在parent的左 ,parent在grandfather的右:左右双旋,cur变黑,grandfather变红
cur在parent的右 ,parent在grandfather的左:右左双旋,cur变黑,grandfather变红
旋转完成以后,规则2、3没有被违反,插入结束
3.记忆方法
只有当parent存在且为红时,才会按需变色或旋转+变色
细分三种情况讨论,但(2)、(3)两种情况的操作一致,(1)和(2)(3)不一致,所以
要区分情况1和情况2、3
情况1和情况2、3是以 讨论 uncle 为中心,而只有通过parent与grandfather的连接情况才能找到uncle,所以
操作的思路是,先 区分parent的位置并找到uncle,再区分情况1和情况2、3
//控制红黑节点
while (parent && parent->_col == RED)
{
Node* grandfather = parent->_parent;
//区分parent的位置
if (parent == grandfather->_left)
{
Node* uncle = grandfather->_right;
//区分情况(1)和(2)(3)
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else//uncle 不存在 或者 存在且为黑
{
// g
// p
//cur
if (cur == parent->_left)
{
RotateR(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
// g
//p
// cur
else
{
RotateL(parent);
RotateR(grandfather);
parent->_col = grandfather->_col = RED;
cur->_col = BLACK;
}
break;
}
}
else//parent == grandfather->right
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
uncle->_col = parent->_col = BLACK;
grandfather->_col = RED;
cur = grandfather;
parent = cur->_parent;
}
else//uncle 不存在 或者 存在且为黑
{
//g
// p
// cur
if (cur == parent->_right)
{
RotateL(grandfather);
grandfather->_col = RED;
parent->_col = BLACK;
}
// g
// p
// cur
else
{
RotateR(parent);
RotateL(grandfather);
parent->_col = grandfather->_col = RED;
cur->_col = BLACK;
}
break;
}
}
}
_root->_col = BLACK;旋转结束即跳出循环没有违反规则,但是在uncle 存在且为红的向上调整操作中
若parent为空,跳出循环,此时cur即是根节点,但是此时的cur为红色节点,需要进行修正
_root->_col = BLACK;
5.验证红黑树
(1)通过枚举我们已经限制了节点颜色非黑即红
(2)所以我们要验证根节点的颜色为黑色
(3)验证树中没有连续的红色节点:
当前节点与其父亲节点的颜色不全为红即可,
(4)验证从任意节点到其所有空节点的路径上,黑色节点数量相同:
只要验证根节点到每个空节点的路径上,黑色节点的数目一致即可
沿着最左路径记录黑色节点的数目,然后进行前序遍历,遇到空时就进行比较
bool IsRBTree()
{
if (!_root)
{
return true;
}
//验证根节点的颜色为黑色
if (_root->_col != BLACK)
{
cout << "根节点不为黑色" << endl;
return false;
}
//最左路径的黑色节点数目作为基准值
int BenchMark = 0;
Node* cur = root;
while (cur)
{
if (cur->_col == BLACK)
++BenchMark;
cur = cur->_left;
}
return CheckColor(_root, 0, BenchMark);
}
bool CheckColor(Node* root, int blacknum, int benchmark)
{
if (!root)
{
//blacknum是传值传参,
//节点为空,blacknum记录的就是根节点到该空节点的路径中黑色节点的数目
if (blacknum != benchmark)
{
cout << "不同路径黑色数目不同" << endl;
return false;
}
return true;
}
if (root->_col == BLACK)
++blacknum;
//验证树中不存在连续的红色节点
if (root->_col == RED && root->_parent && root->_parent->_col == RED)
{
cout << root->_kv.first << " 和它的父亲 " << root->_parent->_kv.first
<< " 都是红色节点" << endl;
return false;
}
//前序遍历
return CheckColor(root->_left, blacknum, benchmark)
&& CheckColor(root->_right, blacknum, benchmark);
}