Table of Contents
- 前言:
- 什么是图:
- 图的基础概念:
- [Part 1.有向图、无向图、加权图](#Part 1.有向图、无向图、加权图)
- [Part 2.度,入度,出度,联通图](#Part 2.度,入度,出度,联通图)
- 图的存储:
- [Part 1.邻接表存储](#Part 1.邻接表存储)
- [Part 2.邻接矩阵存储](#Part 2.邻接矩阵存储)
- 结语:
前言:
众所周知,图论,是算法与数据结构高度统一的一部分,也是一块硬骨头;
但是,我们这些学计算机的人,不就是应该迎难而上吗;
所以,在开学前的最后4天,本蒟蒻准备开始啃图论了;
读完本文,你将对图和图的基础概念有一个深刻的认知;
前置知识:无(不过,如果你已经知道'集合'和'二元关系'这两个词,阅读体验会更丝滑)
什么是图:
我们先讲讲为什么会有图
想象一下,现在有一个巨大的社交网络,其中每个人都与若干个人有联系
如果是你,你会怎么表示它的数学模型呢(或者说,你会怎样把它抽象出来,使它易于表示、观看);
一个很显然的做法是:将人抽象成点,将人与人的关系抽象成线,两个点有连线,当且仅当这两个点代表的两个人有联系;
也就是说,两个人有联系时,我们就把他们连起来;
那么,恭喜你,发明了图!
图就是将复杂的关系简单化的一种数据结构,能够轻而易举地看出复杂关系,并加以研究 ;
比如如下两个图:
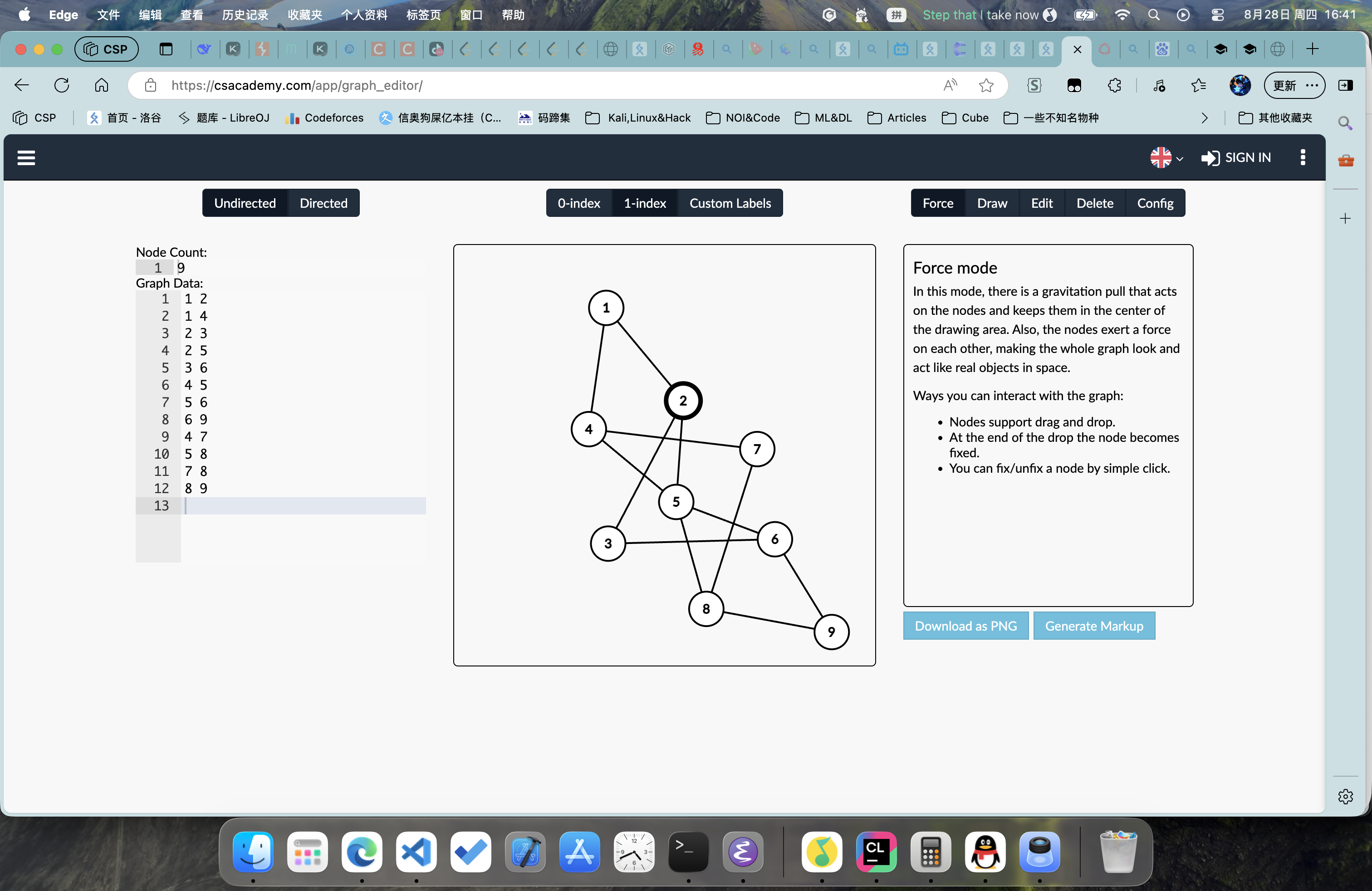
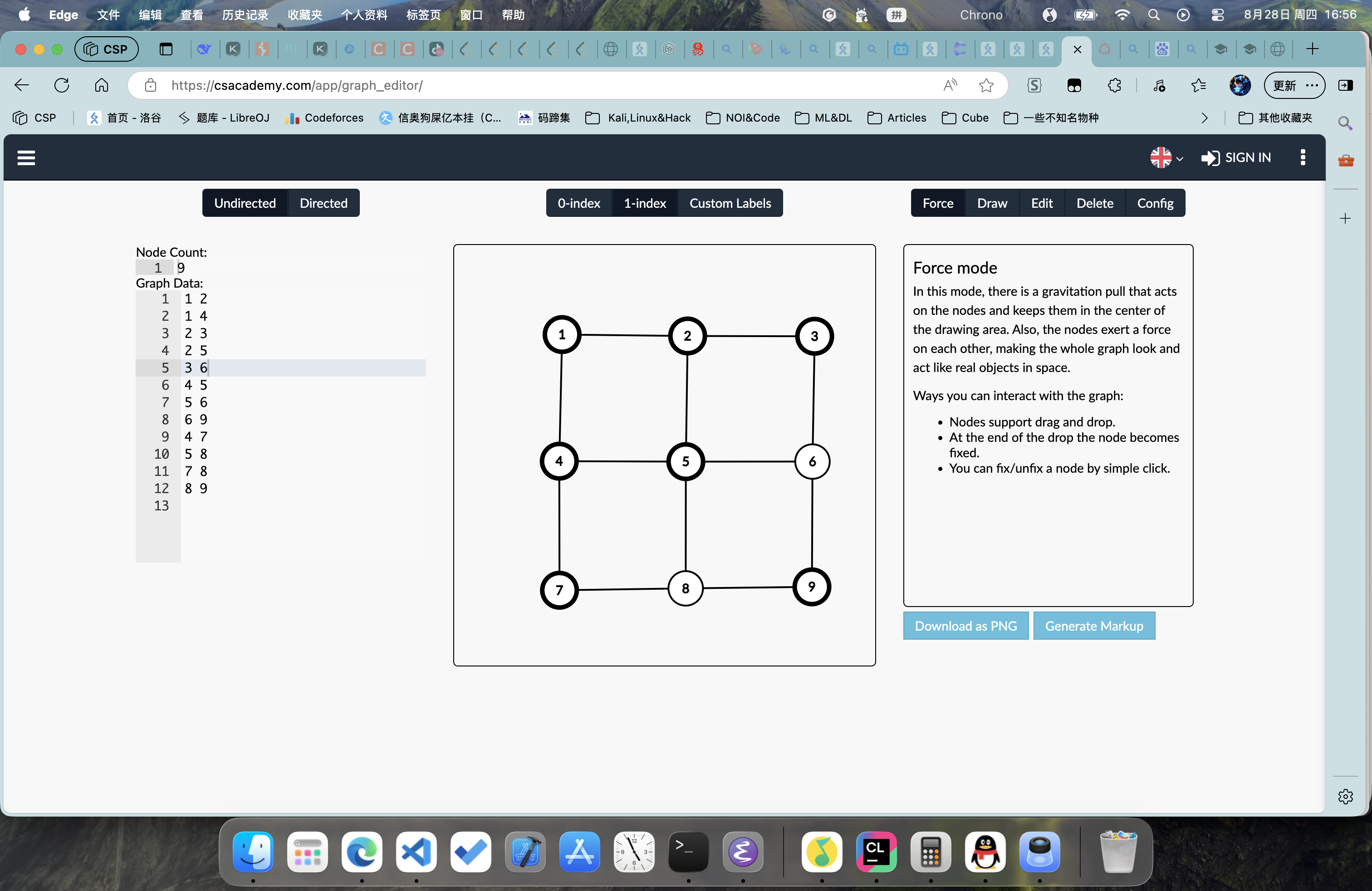
仅看第一张图,你完全不知道这是什么;
现在我告诉你,它和第二张是等价的;
相信,通过这个例子,你能够知道图的力量了;
图还有一个非常著名的应用:地图软件(当然,这都老生常谈了),我们将任何一个位置抽象成点,两点之间的线的长度就是两点之间的距离,随后找出起点和终点的最短路即可;
通过这两个例子,不难发现,每张图都有点、边这两个东西,因此,图的定义是这样的:
**给定两个集合: \(V、E\) ,其中 \(V\) 存放所有的点, \(E\) 存放所有的边,图 \(G\) 就是这两个集合的组合:\(G = (V,E)\) ;
**
我们依次解释里面的几个地方:
由于 \(V\) 存放所有的点,我们称 \(V\) 为点集,这与高中数学中常见的点集是一样的;
由于 \(E\) 存放所有的边,我们称 \(E\) 为边集;
怎么表示一个边呢?若有两个点 \(u,v\) , \(u,v\) 之间的边用**无序的对** \({u,v}\) 表示,所以, \(E\) 大概是这样的: \(E = \{\{u_1,v_1\},\{u_2,v_2\},\cdots \{u_n,v_n\}\}\) ;
显然,其中的每个点必须是 \(V\) 中的一个点,否则就是没有意义的;
一些补充:点,有的地方也叫做顶点、节点;
图的基础概念:
不要一听到基础概念就跑路,仅仅去罗列概念是没有用的,看完就会忘;学算法更重要的是理解本质;
Part 1.有向图、无向图、加权图
那么仍然是根据地图和社交网络的例子:
小A认识小B代表小B认识小A吗,显然不是;
一条路是否可以是单行道呢,显然可以;
到目前为止,我们把边画成了"没有箭头"的线段
------这意味着"张三认识李四"与"李四认识张三"被当成同一件事
那么怎样表示小A认识小B,而小B不认识小A呢? 我们可以画一个小A指向小B的箭头,这样就代表示小A认识小B,小B什么也不做(没有指向小A的箭头),这就表示,小B不认识小A;
再比如在地图中,若是AB两点只允许A通向B,我们就将A指向B,这代表从A到B有路;
所以对于某些情况,边是有指向性的,我们把这样的图叫做有向图;
相应的,边没有指向性的图就叫做无向图;
那么无向图和有向图有什么区别呢?
注意到:在定义中,我提到了:边使用无序的对表示,这表明了,由 \(u\) 向 \(v\) 连接还是由 \(v\) 向 \(u\) 连接都无所谓,是一样的;
但在有向图中,这并不等价,我们需要定义边究竟是谁指向谁,所以,这里需要使用有序对,我们使用小括号,记为 \((u,v)\) ,代表有一条从 \(u\) 指向 \(v\) 的边;
也就是说,之前的定义是无向图的定义,而修改为有序对之后就是有向图的定义;
到目前为止,这张地图、社交网络完整了吗?
显然,没有,地图需要比例尺来确定两点间的距离,社交网络也需要一个值衡量两个人的好感度,这就意味着,我们的边需要一个长度,它代表着,两点的距离、两个人的好感度;
我们把这种边长有值的图叫做赋权图、加权图 ,权,就是这条边的长度,如图:
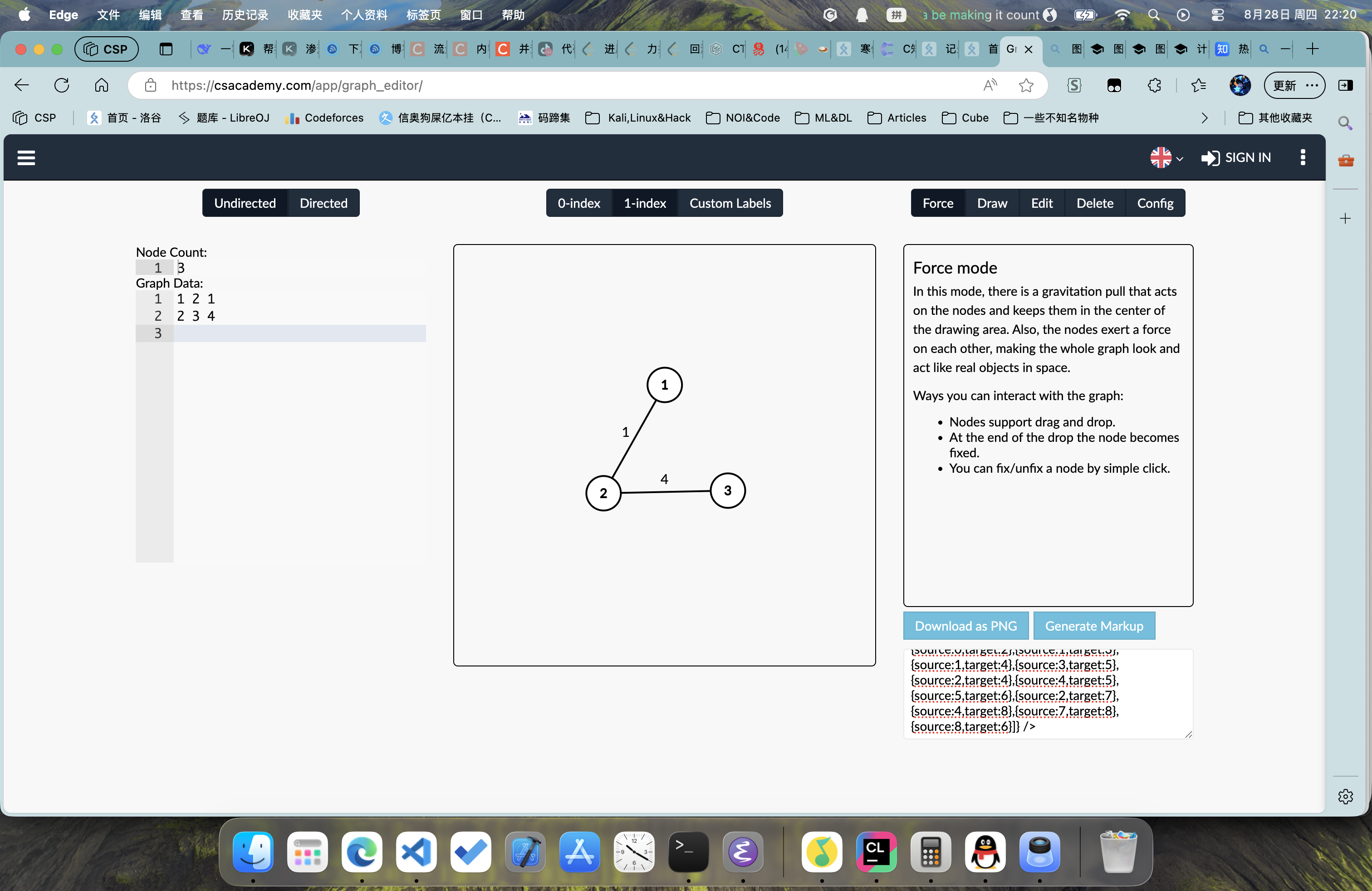
这样,我们就完成了地图与社交网络的表示;
Part 2.度,入度,出度,联通图
接下来,我们介绍另一个概念:度 ;
何为度呢,度就是与一个点有关系的点的数量 ;
换言之:就是与这个点相连的边的数量;
特别的,在有向图中,指向这个点(以这个点为终点)的边的数量叫做这个点的入度;反之,从这个点出发的边的数量就是这个点的出度;
也就是说,只有有向图分入度、出度,无向图只有度;
我们称无向图中度数为偶数的点为 偶点,度数为奇数的点为奇点;
再引入一个问题,就是著名的一笔画问题:给你一张图,如何能判断这张图是否能一笔画完;
即:从某点出发,经过每条边**恰好**一次,最后停在一个点;
欧拉给出了一笔画定理:当且仅当一个图联通,并且这张图上奇点个数为0或2时可以一笔画成;
这是为什么呢?
- 首先,什么是连通:故名思义,就是从一点出发,可以沿着边到达一些点后继续沿着边前进,能够达到所有的点,换言之,就是没有任何一个孤立的点,我们称这张图连通;
- 随后,为什么奇点个数为0时可以一笔画:
想象一下,你正在一笔画一个图形。每当你用笔经过一个顶点时,必定是"一进一出"
假设你从起点A出发。每当你的路径进入一个顶点(比如B),就必须有一条"尚未使用"的边让你离开B(除非B是终点)。这个"进入"和"离开"的动作,会消耗掉与顶点B相连的两条边。
因此,对于路径上的中间顶点(不是起点和终点的点),与之相连的边必须成对出现,即它的度数必须是偶数
那么起点和终点呢?
如果你的路径最终要回到起点(形成回路),那么起点在最初"离开"了一次,最终又"进入"了一次。这一出一进同样消耗了两条边。所以,起点/终点也必须是偶度数。
因此,存在欧拉回路(一笔画的时候起点就是终点)的图,所有顶点都必须是偶度数;
- 为什么奇点个数为2可以一笔画:
现在,假设你的路径不需要回到起点。那么,起点和终点将是两个不同的顶点。
起点:你从这里出发,只"离开"不"进入"。因此,与起点相连的边被消耗掉的次数是奇数(第一次离开,之后可能进出多次,但总次数为奇)。
终点:你最终到达这里,只"进入"不"离开"。因此,与终点相连的边被消耗掉的次数也是奇数。
中间顶点:依然是"一进一出",消耗偶数条边。
所以,在这种情况下,整个图有且只能有两个顶点拥有奇数度数,它们分别就是路径的起点和终点
证毕.
相信通过这个例子,你能够深刻地理解图论的一些基础概念;
一些补充:联通,也写做「连通」,大部分资料都是使用「连通」;
图的存储:
Part 1.邻接表存储
接下来我们讲如何把一张图存在计算机中,如果是你,你会怎么办呢?
大部分人的想法是:遵循图的定义,使用一个集合存点,另一个集合存边,但是,这么做的代价是:每次从一个点到另一个点,需要查看所有的边才行(这样才能找到与这个点相连的边);
那么怎么优化一下呢?
我们可以给每个点都开一个集合,里面存放与这个点相连的边;
更进一步,对于无向图,由于这里面的边都与这个点相连,我们可以只存另一个点,优化内存;对于有向图,这个点的集合存放的就是以这个点为起点的边,同样,由于都是以这个点为起点,我们也可以只存另一个点;
那么,恭喜你,发明了图的邻接表存储;
邻接表存储:给每个点都开一个数组,数组的成员即为与这个点相连的点的编号,若图有权,再另开一个权数组,对应存权值;
邻接表的邻接,就是「这条边与这个点相邻、相接」的意思;
补充:由于需要兼容有向图,并且更好地操作,如果是无向图,我们需要在u的集合存v,在v的集合存u;
Part 2.邻接矩阵存储
众所周知,没有绝对完美的结构,每种方式总有缺点,如果没有,那么这种结构一定非常复杂;
那么邻接表又有什么缺点呢?
我们先想想对于图,会有什么操作:最简单的,就是查询 \(u,v\) 间是否有边;
邻接表的查找,很显然,需要遍历u的集合的所有成员,也就是 \(O(n)\) ,更准确地讲,这跟u的度有关,我们把一个点u的度记为 \(d(u)\) ,那么时间复杂度是 \(O(d(u))\) ;
有一种做法,可以将「查询 \(u,v\) 间是否有边」的时间复杂度降低至 \(O(1)\) ,而根据我们的经验,这一定是要付出一些代价的;
这次的代价是:空间;
我们以空间换时间,定义一个矩阵 \(G\) , \(G_{i,j} = 1\) 代表有一条从i到j的边(仍然是为了兼容有向图),若是这是加权图,我们将1改为权即可;
这种方法简单、粗暴,弊端也很明显:当一个图点数很多,而边很少的时候,会浪费大量的空间;
但这正是邻接表的优点;
我们做一个总结:在稀疏图(即点多、边少)中,我们使用邻接表,在稠密图中,我们使用邻接矩阵;
结语:
"人生如棋,我愿做卒"
"行动虽缓,可谁曾见我后退一步!"
这篇文章只是对图的一个初步认识,接下来会陆续更新图论算法;
如有笔误,烦请不吝赐教
Upt 2025.8.28 22:22