AFramework for Multi-stage Bonus Allocation in meal delivery Platform
本文针对美团每日数十万单因无人接单而被取消的痛点,提出"多阶段动态奖金分配"框架:先用半黑盒模型预估奖金---接单概率关系,再用拉格朗日对偶动态规划离线算出阶段乘子,最后在线实时为每一单分配合适奖金;离线与线上 A/B 测试均表明,该方案可在预算内将订单取消率降低 25% 以上。
问题场景
平台每天约 16.5 万单因无人接单而被取消(NA-canceled)。
一笔订单从推送到司机端开始,最多可以经历 |T| 次奖金调整(阶段)。
每阶段:
-- 若司机接单,则订单成功;
-- 若顾客取消,则订单失败;
-- 若二者均未发生,则进入下一阶段继续等待。
平台需在月度总奖金预算 B 之内,为每单在每个阶段实时决定奖金 c_i,t,以最大化最终被接单的期望订单量。
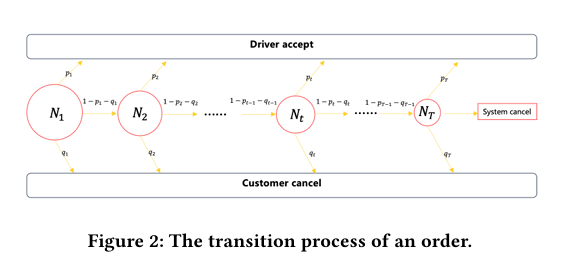
状态转移与概率拆解
接受概率 p_i,t(c_i,t)
采用 Logistic 形式:
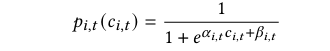
其中:
α_i,t<0(奖金越高,概率越大);
α_i,t、β_i,t 由神经网络同时学习,但使用不同隐藏层:
-- α_i,t 仅用"有奖金样本"更新;
-- β_i,t 仅用"无奖金样本"更新,以避免样本不平衡。
输入特征:
c_i,t:阶段 t 分配的奖金;
x_i,t:订单上下文(距离、ETA、供需、天气、司机密度等)。
取消概率 q_i,t
用 XGBoost 对已进入阶段 t 的订单建模;
将预测概率按 0.05 区间分桶,统计桶内正样本比例作为最终 q_i,t。
阶段转移概率
订单能进入阶段 t 的概率:
Π_{k=1}^{t-1}(1-p_i,k-q_i,k)。
因此在阶段 t 被接单的联合概率:
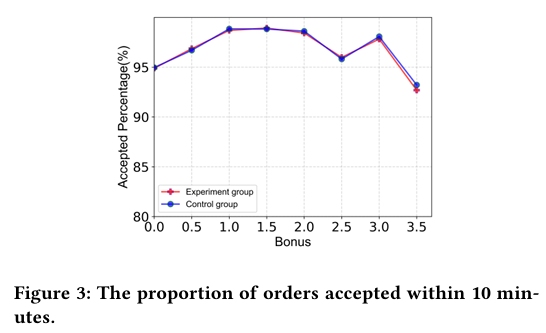
Π_{k=1}\^{t-1}(1-p_i,k-q_i,k)\] · p_i,t。 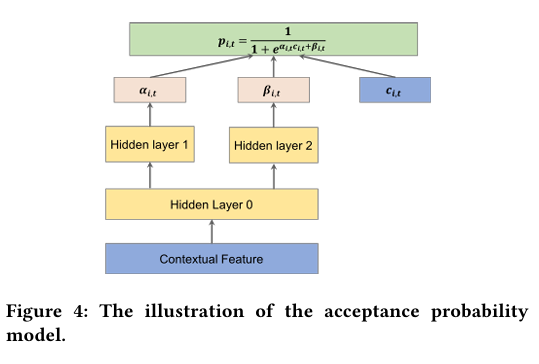 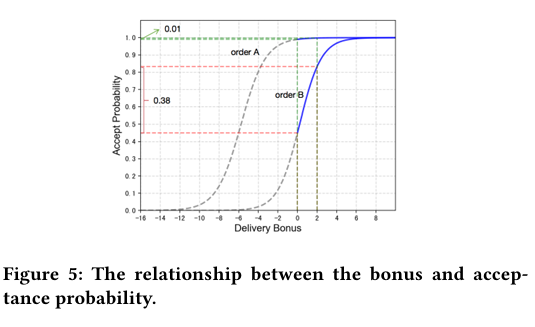 ## 数学规划模型  ## 关键建模假设 阶段独立:阶段 t 的接受概率仅受该阶段奖金 c_i,t 影响,不受其他阶段奖金或其他订单奖金影响(经 0--3.5 元区间 A/B 验证,司机在前 10 分钟内行为无显著差异,假设成立)。 奖金只在订单被最终接单时才实际支付,因此约束采用"期望成本"而非"实际成本"。 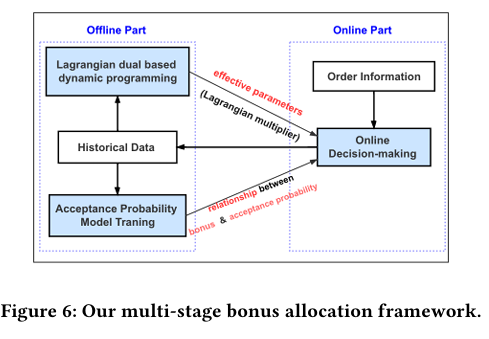 ## 模型特色 同时刻画"接单-取消-继续等待"三重随机事件; 利用 Logistic + XGBoost 的半黑盒结构兼顾解释性与精度; 训练时针对奖金/非奖金样本分别更新不同网络层,解决极端样本不平衡。 ## 总体思路 把原非凸多阶段问题拆成两步: (1) 阶段间预算切分:用离散动态规划(DP)离线决定"每一阶段最多花多少钱"; (2) 阶段内订单级奖金:用拉格朗日对偶理论在线实时决定"给每一单多少奖金"。 通过一维降维(把高维概率向量压缩成平均概率)和凸等价变换,将 DP 状态转移公式化成 O(B·\|T\|) 的递推;再用二分法求单阶段最优乘子 λ_t(·)。 在线阶段直接代入离线求得的 λ_t\*,把整体问题拆成 \|N_t\| 个独立的一维枚举,复杂度 O(1)/单,可并行。 ## 离线算法流程  ### 单阶段子问题 BA(N_t, B̃): 决策变量:概率向量 p_i,t,c_i,t(p_i,t) 为凸函数。 目标:max Σ p_i,t 约束:Σ p_i,t·c_i,t(p_i,t) ≤ B̃ 通过凸对偶(零对偶间隙)与二分法(Algorithm 2)求最优 λ_t(B̃) 与最优值 g_t(B̃)。 ### DP 递推: G_t(B̃)=max_{k=0...B̃} {g_t(k)+(\|N_{t+1}\|/\|N_t\|)·G_{t+1}(⌊\|N_t\|/\|N_{t+1}\|·(B̃-k)⌋)} 其中 \|N_{t+1}\|=\|N_t\|−g_t(k)−Q_t 反映剩余订单量。 复杂度:O(B·\|T\|) 存储 + O(B·\|T\|·\|N_t\|) 计算,B 为离散预算级数。 ## 在线算法 代入离线 λ_t\*,把原问题拆成 \|N_t\| 个独立一维问题: min_{0≤c_i,t≤C_i\^u} \[λ_t\*·p_i,t(c_i,t)·c_i,t − p_i,t(c_i,t)
枚举有限候选奖金(0...C_i^u)即可得最优 c_i,t*,复杂度 O(1)/单,可并行。

预算滚动修正(Periodic Control)
每日离线重算:用"上月同日"数据训练,预算=剩余预算/预计剩余单量×过去 30 天单量。
实时微调:支出>110%预算时按比例下调奖金,<90%时上调,确保月度不超支。
离线实验设计
数据集
• 4 座典型城市:兰州(46 978 单)、南昌(71 427 单)、威海(120 017 单)、成都(258 612 单),覆盖一周内全部订单。
• 预算口径:统一折算为"每单平均可用奖金",保证不同城市可比。
• 订单生命周期:0--50 min,8 个阶段,每阶段约 6 min 可调一次奖金。
核心指标
• NA-canceled 订单量(无人接单导致顾客取消)。
• 总奖金消耗曲线。
结果对比
• 无奖金:NA-canceled 为基线 100%。
• 统一奖金(每单固定额度):NA-canceled 降幅 ≈30%。
• 单阶段奖金(只在第 1 阶段一次性加价):NA-canceled 降幅 ≈45%。
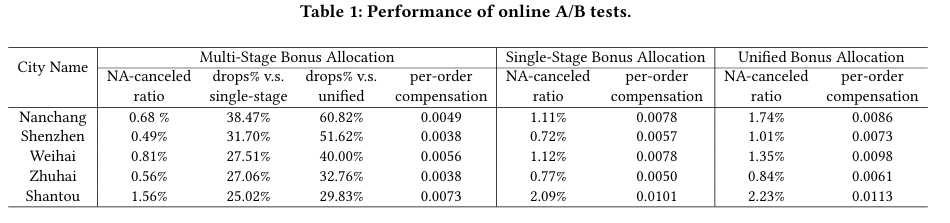
• MSBA 多阶段动态:NA-canceled 降幅 >60%;与单阶段相比再降 ≈20%,与统一奖金相比再降 ≈40%。
• 订单量越大的城市,MSBA 优势越显著。
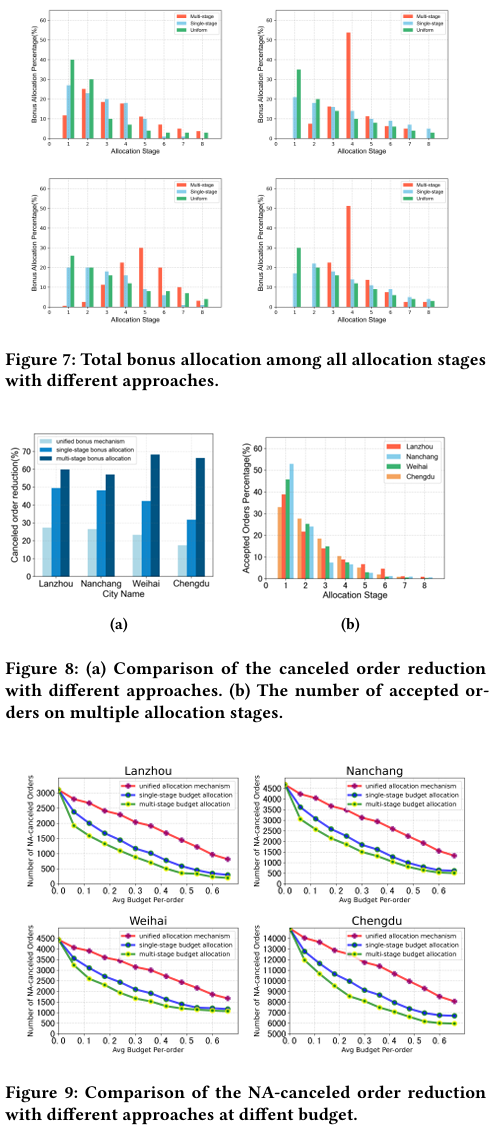
奖金-阶段分布
• 第 1 阶段奖金占比低:高接受概率的"订单 A"立即被接,无需补贴。
• 第 2--4 阶段奖金占比高:大量"订单 B"需激励。
• 第 5 阶段后奖金递减:剩余订单减少,边际收益下降。
预算敏感性
• 低预算(<0.15 元/单):MSBA 仍可将 NA-canceled 降至单阶段/统一奖金的 50% 以下。
• 高预算(>0.3 元/单):三种方法趋同,但 MSBA 仍保持 5--8% 的额外优势。
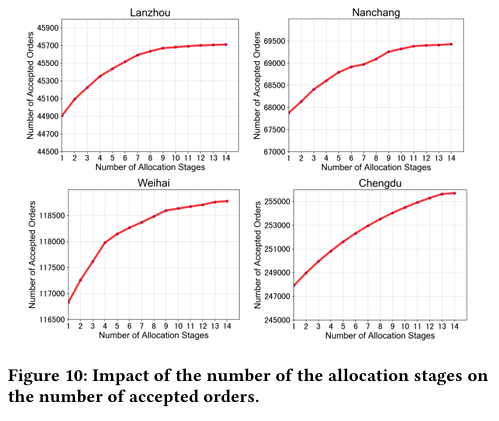
阶段数敏感性
• 阶段数从 2 增至 10,接受订单量单调上升;>10 后增益趋缓且司机体验下降(奖金调整过频)。
• 推荐:8--10 阶段为最佳折中。
结论
针对外卖平台"无人接单"导致的巨额取消单量,本文提出 MSBA 框架:用半黑盒模型刻画接单概率,离线 LDDP 算法求阶段乘子,在线 O(1) 实时为每单定价;离线与线上 A/B 均验证其可在 0.2 元/单预算内将取消单量再降 25% 以上,现已全量部署于国内最大外卖平台。