文章目录


💗博主介绍:计算机专业的一枚大学生 来自重庆 @燃于AC之乐✌专注于C++技术栈,算法,竞赛领域,技术学习和项目实战✌💗
💗根据博主的学习进度更新(可能不及时)
💗后续更新主要内容:C语言,数据结构,C++、linux(系统编程和网络编程)、MySQL、Redis、QT、Python、Git、爬虫、数据可视化、小程序、AI大模型接入,C++实战项目与学习分享。
👇🏻 精彩专栏 推荐订阅👇🏻
🌟算法相关题目点击即可进入实操🌟
感兴趣的可以先收藏起来,请多多支持,还有大家有相关问题都可以给我留言咨询,希望希望共同交流心得,一起进步,你我陪伴,学习路上不孤单!
前言:
这些题目摘录于洛谷,好题,典型的题,考察各类算法运用,可用于蓝桥杯及各类算法比赛备战,算法题目练习,提高算法能力,补充知识,提升思维。
锻炼解题思路,从学会算法模板后,会分析,用到具体的题目上。
对应题目点链接即可做。
本期涉及算法:哈希表,前缀和,背包问题,特殊枚举,字符串函数运用与细节处理,贪心算法 。


题目清单
1.火柴棒等式
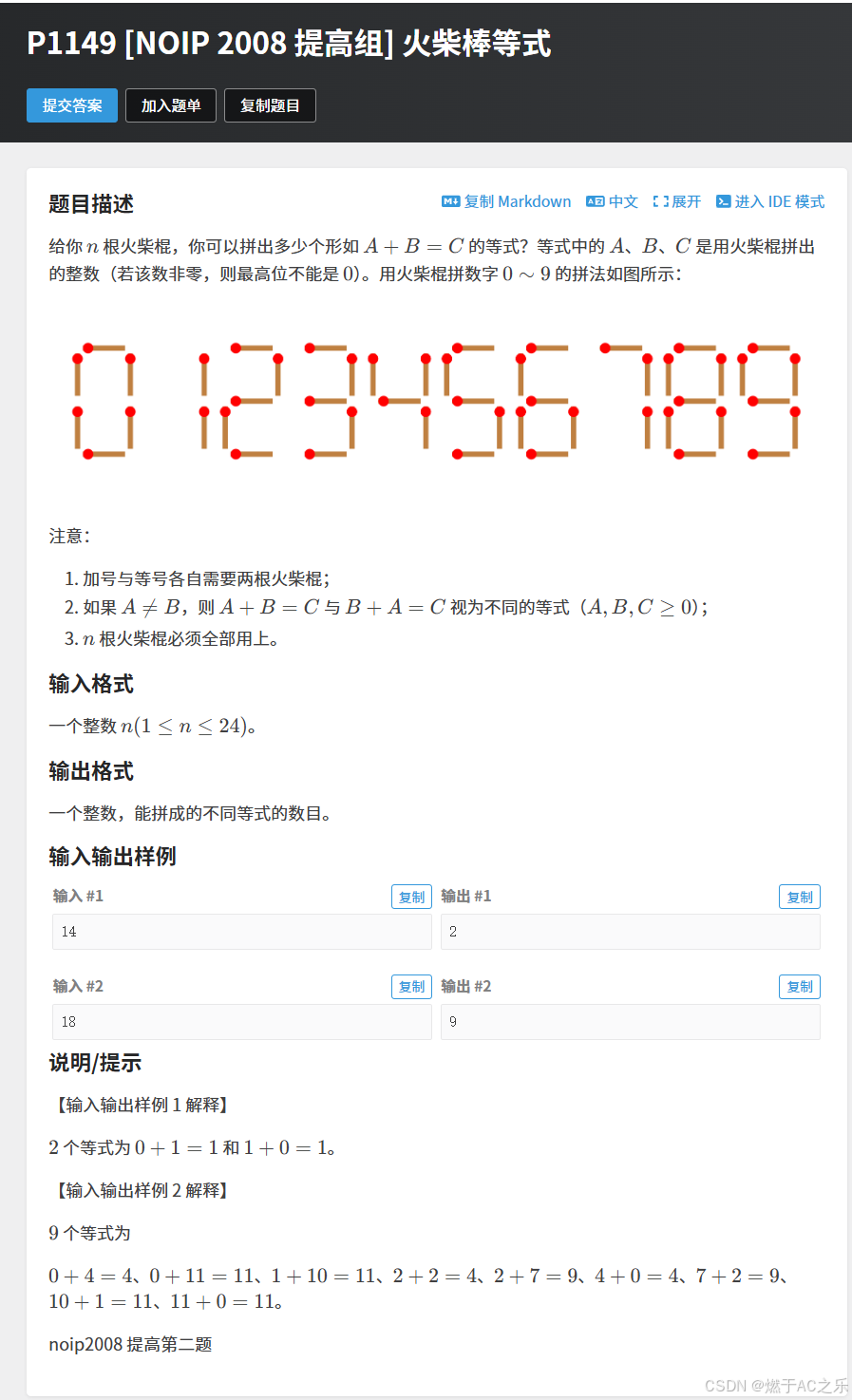
题目: P1149 [NOIP 2008 提高组] 火柴棒等式
解法:暴力枚举
n的最大值为24,由于 "+" 和 "=" 要用掉4根火柴,剩下20根火柴。 进行估算, 1111 + 1 = 1112 要用掉25根火柴,所以四位数以上不考虑。711 + 0 = 711,满足条件,所以枚举所有1~1000即可,判断是否刚好等于n。
细节: 因为不能有前导0,要对0特殊处理
代码:
cpp
#include <iostream>
using namespace std;
int n;
int a[] = {6, 2, 5, 5, 4, 5, 6, 3, 7, 6};
int calc(int x)
{
if(x == 0) return 6; //边界处理
int sum = 0;
while(x)
{
sum += a[x % 10];
x /= 10;
}
return sum;
}
int main()
{
cin >> n;
int ret = 0;
for(int a = 0; a <= 1000; a++)
{
for(int b = 0; b <= 1000; b++)
{
int c = a + b;
if(calc(a) + calc(b) + calc(c) + 4 == n)
ret++;
}
}
cout << ret << endl;
return 0;
}2.导弹拦截
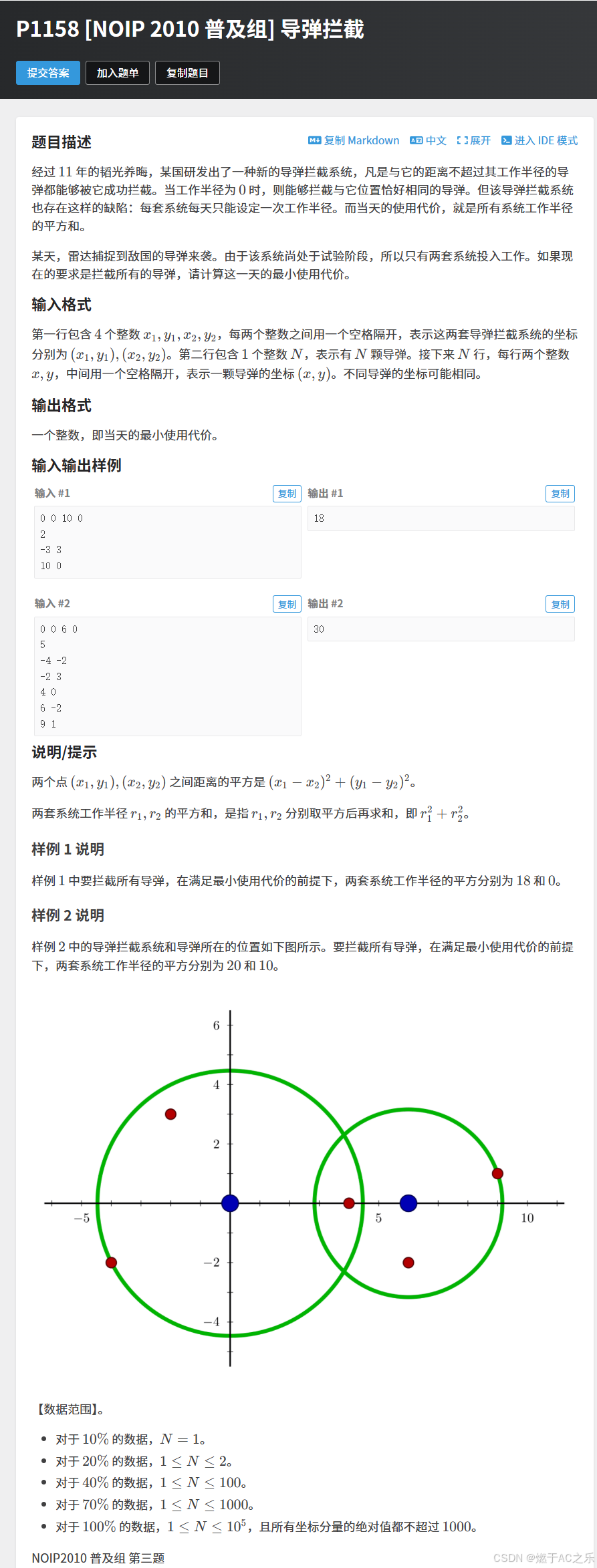
题目: P1158 [NOIP 2010 普及组] 导弹拦截

解法:特殊枚举 + 排序
模型转化,将导弹,拦截系统位置和拦截区域范围看成点,圆心,和半径。 问题就转化为包含所有的点,求出两个半径的最小平方和。
首先,这里很容易想到错误的贪心策略,就是枚举所有的导弹,将每个导弹分配到近的那个中心区域,这样看似满足最短距离,实则错误,如下:
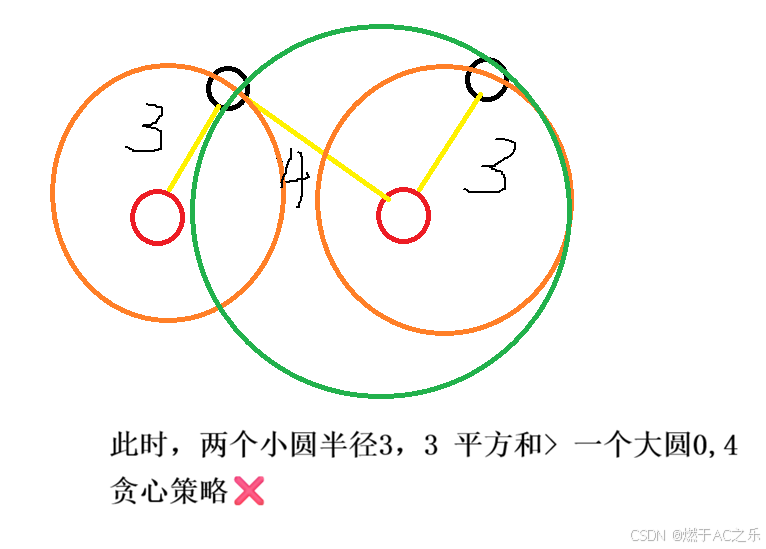
这道题的枚举策略,思路很特别,需要好好积累。
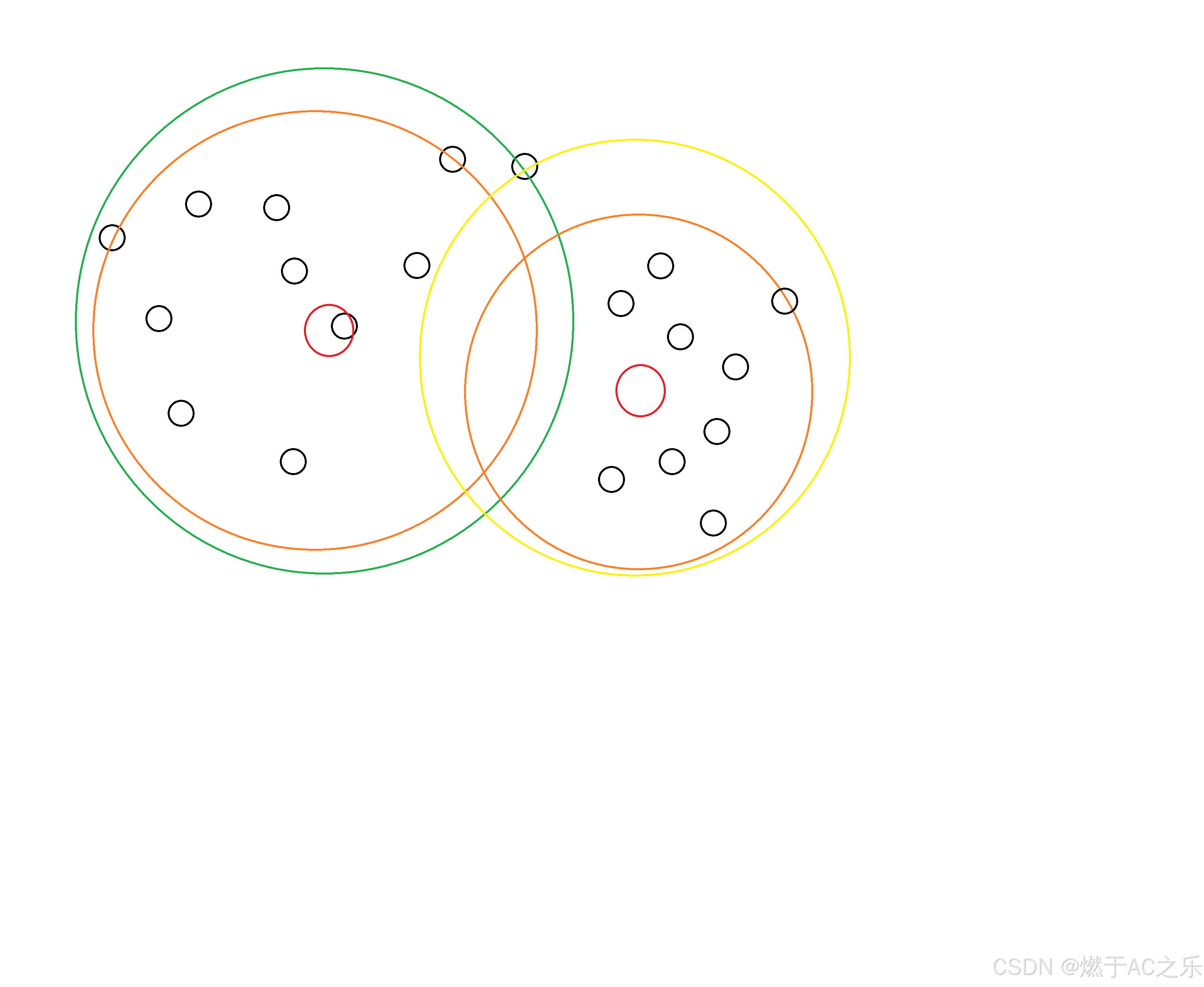
就是固定一个圆的半径,那么它能包含的点就固定,另外一个原的半径就为圆心到未包含的最远的点的距离。
我们可以现予处理出所有的点到第一个圆心的距离,然后从大到小进行排序,对其进行枚举,相当于第一个圆的区域范围不断变小,至少放出一个点给第二个圆包含,每次进行max,求第二个圆范围,再不断min更新结果,枚举处所有情况的最小值。
注意: 循环到n+1,处理第一个圆半径为0的边界 。
代码:
cpp
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 1e5 + 10;
int x1, y1, x2, y2, n;
struct node
{
int x, y, d;
}a[N];
int calc(int i, int x, int y)
{
int dx = x - a[i].x;
int dy = y - a[i].y;
return dx * dx + dy * dy;
}
bool cmp(node& a, node& b)
{
return a.d > b.d;
}
int main()
{
cin >> x1 >> y1 >> x2 >> y2;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i].x >> a[i].y;
a[i].d = calc(i, x1, y1);
}
sort(a + 1, a + 1 + n, cmp);
int ret = a[1].d;
int r2 = 0;
for(int i = 2; i <= n + 1; i++) //循环到n+1,处理第一个圆半径为0的边界
{
int r1 = a[i].d;
r2 = max(r2, calc(i - 1, x2, y2));
ret = min(ret, r1 + r2);
}
cout << ret << endl;
return 0;
}3.铺设道路
题目: P5019 [NOIP 2018 提高组] 铺设道路
解法:贪心
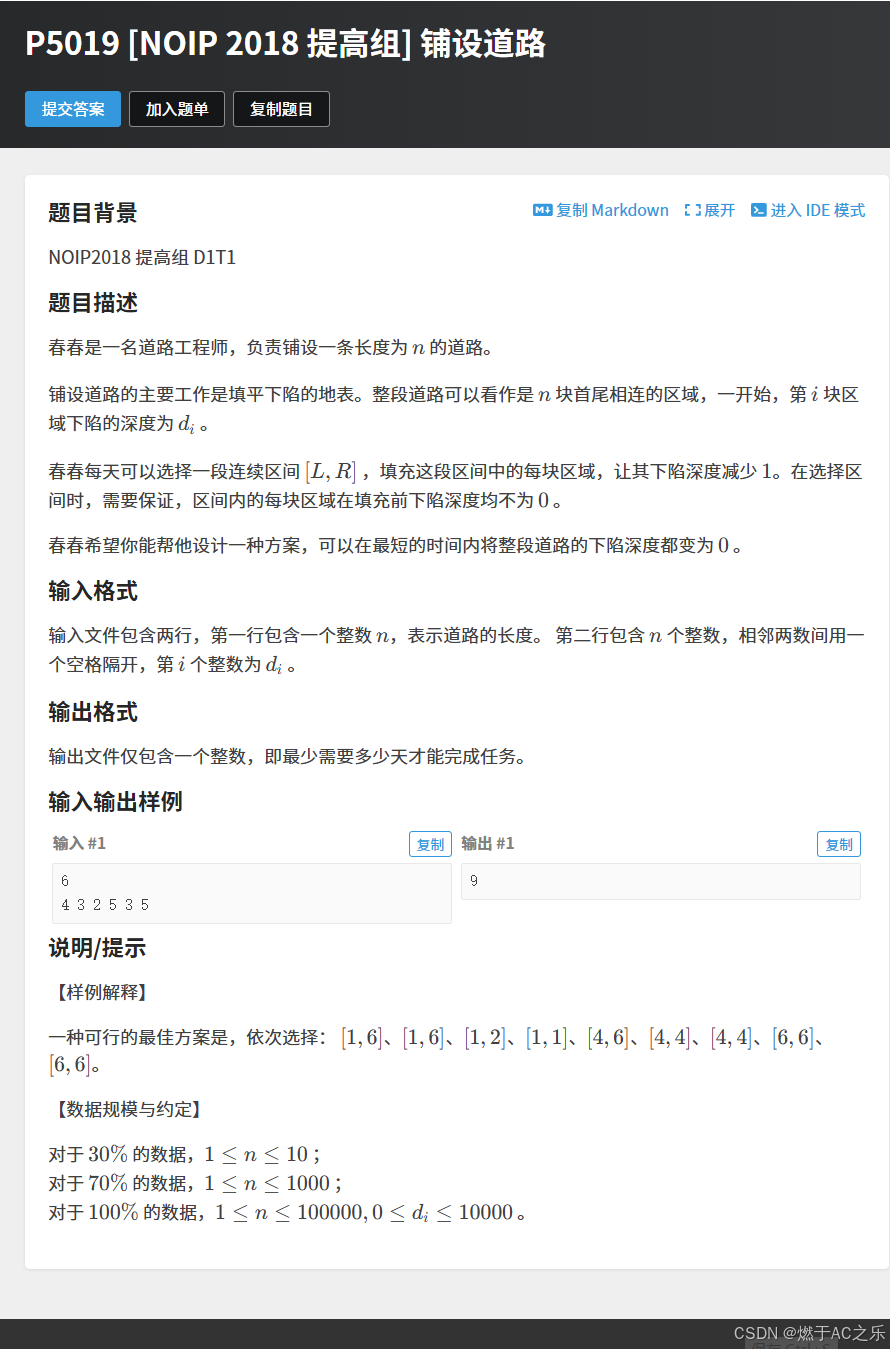
从前往后遍历对于第i个,分两类情况:
1.a[i - 1] < a[i]: 只需要填上a[i] - a[i - 1], 因为a[i - 1] 的部分会在处理a[i - 1]时填上;
2.a[i - 1] >= a[i]: 不需要填,因为前面填a[i - 1]时会填上。
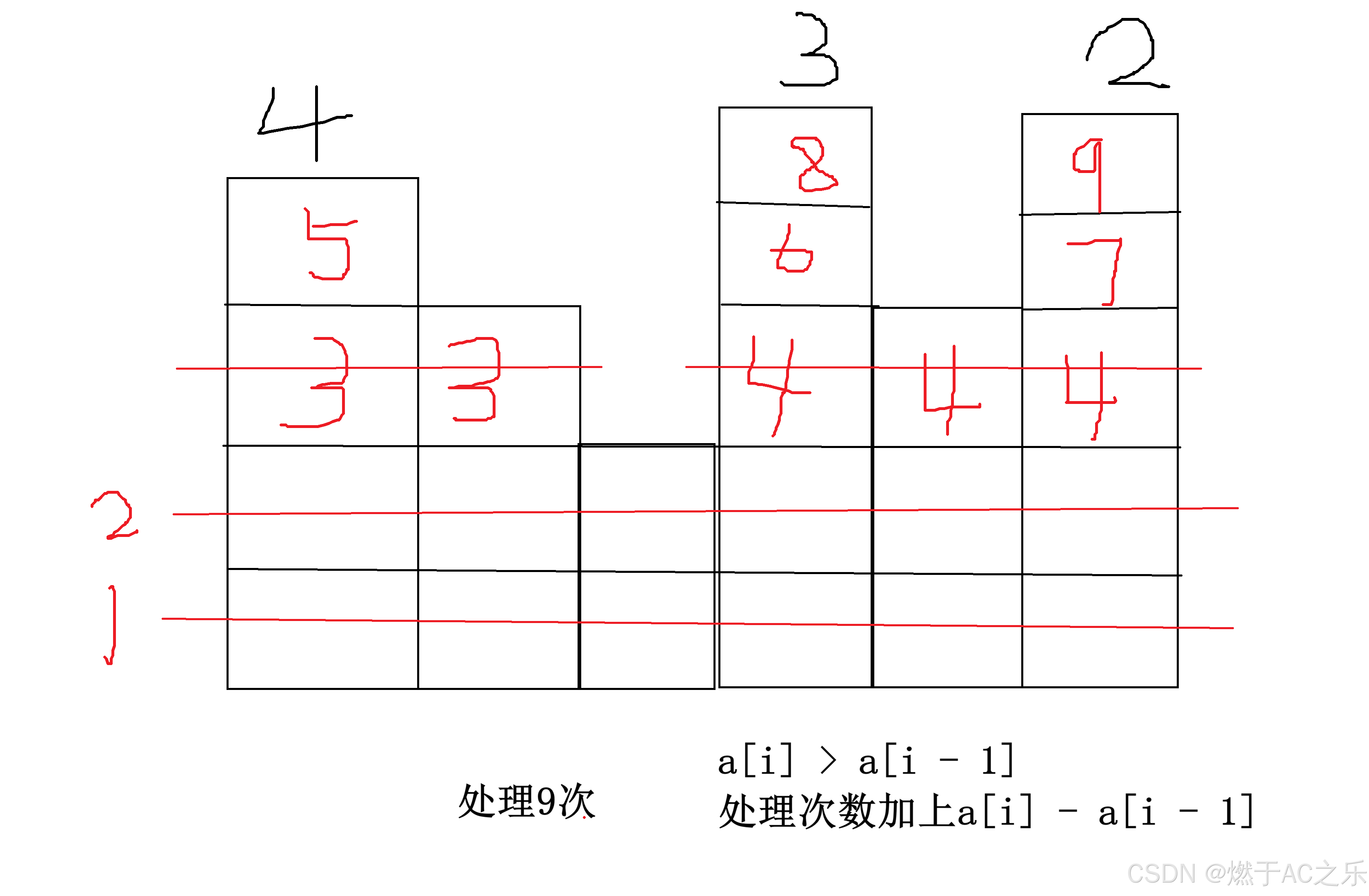
代码:
cpp
#include <iostream>
using namespace std;
const int N = 1e5 + 10;
int n;
int a[N];
int main()
{
cin >> n;
int ret = 0;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
if(a[i] > a[i - 1])
{
ret += a[i] - a[i - 1];
}
}
cout << ret << endl;
return 0;
}4.Shaass and Bookshelf
题目: CF294B Shaass and Bookshelf
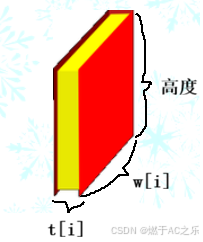
解法:(动态规划)01背包
如果在选择每一本书摆放位置的时候,既考虑上面的宽度,又考虑下面厚度,解决起来非常麻烦。
这里类比"导弹拦截"那道题的的思路。
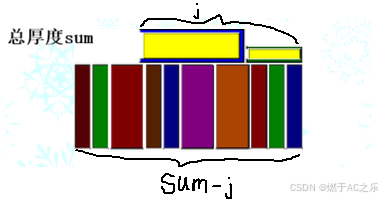
如果看水平放置的书籍,确定下来之后,下面的书籍的厚度是可以用总厚度sum 减去上面书籍的厚度i直接计算出来。这样,我们只用考虑上面书籍的所有厚度下的最小宽度,然后计算对应下面书籍的厚度是否合法即可。计算上面书籍所有可能的厚度下的最小宽度,正好对应01 背包问题。
1.状态表示:
f[i] [j]表示:从前i 个书本中挑选,水平放置的时候,总厚度恰好为j 时,此时的最小宽度。
注意: 处理结果与以往不同,最终结果就是所有符合sum - j >= f[j] 里面,sum - j的最小值。(j越大,sum - j越小,第一个合法的即为最小值 )
2.状态转移方程:
对于i 位置的书籍,有选或不选两种情况:
a.如果不选:那就是在 [1,i − 1] 区间内,去凑厚度恰好为j时的最小宽度 f[i - 1] [j] ;
b.如果选上i 位置书籍:那就是在 [i,i − 1] 区间内,去凑厚度恰好为 j - t[i] 时的最小宽度,然后再加上i 位置宽度f[i - 1] [j - t[i] + w[i];
因为要的是最小值,所以取上面两种情况的最小值。其中第二种情况注意判断是否存在。
3.初始化:
可以把f表初始化为正无穷0x3f3f3f3f,然后f[0] [0]初始化为0。
不合法的状态初始化为无穷大,取最小值的时候就不会影响结果;
f[0] [0]是一个合法的位置,同时也为了让后续填表是正确的。
4.填表顺序:
从上往下每一行,每一行从左往右。
空间优化版本:每一行从右往左。(优化一维,逆序)
代码:
cpp
#include <iostream>
#include <cstring>
using namespace std;
const int N = 110, M = 1e4 + 10;
int n;
int t[N], w[N];
int f[M]; //f[N][M] 优化一维, f[i][j],从前i本书挑选,水平放置厚度为j,此时的最小宽度
int main()
{
cin >> n;
int sum = 0;
for(int i = 1; i <= n; i++)
{
cin >> t[i] >> w[i];
sum += t[i];
}
memset(f, 0x3f, sizeof f);
f[0] = 0;
for(int i = 1; i <= n; i++)
{
for(int j = sum; j >= t[i]; j--) //优化一维,逆序
{
f[j] = min(f[j], f[j - t[i]] + w[i]);
}
}
for(int j = sum; j >= 0; j--) //j越大,sum - j越小
{
if(f[j] <= sum - j) //第一个合法的即为最小值
{
cout << sum - j << endl;
break;
}
}
return 0;
}5.统计单词数
题目: P1308 [NOIP 2011 普及组] 统计单词数
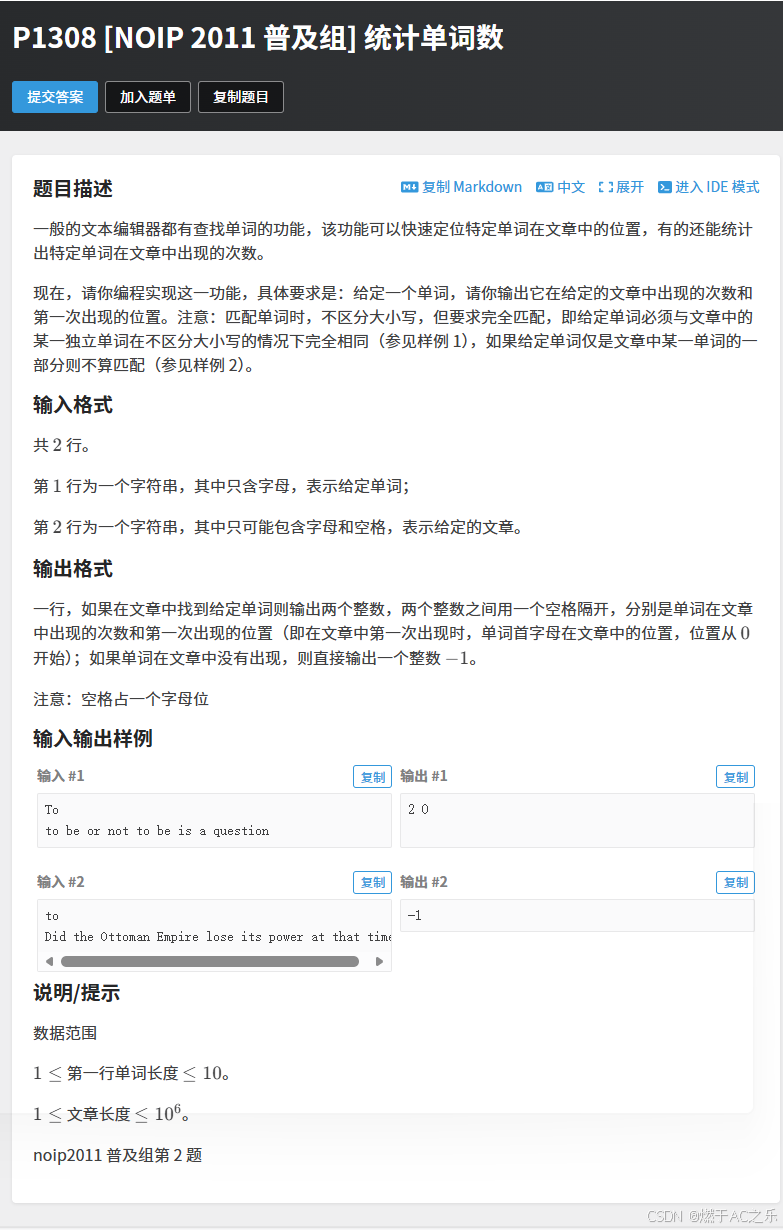
解法:模拟 + 字符串函数t.find(s)
细节处理:1.读入两行字符串,要用getchar()函数 读取处理"\n";2. 第二行有空格 ,要用getline(cin, string) 读取。3.这里对其精妙的处理方法,预处理目标字符串和查找字符串首尾加上' '(空格),这样就不会出现所查找的字符串是文章单词的部分; 4.对find()的运用,t.find(s)是在字符串t中从起始位置查找s字符串出现的第一个位置并返回,可以用下标first存结果(第一个的位置),pos++,找后面的位置,t.find(pos,s)。
代码:
cpp
#include <iostream>
using namespace std;
int main()
{
string s, t;
cin >> s;
getchar(); //读入换行符
getline(cin, t); //要读空格
//预处理
s = ' ' + s + ' ';
t = ' ' + t + ' ';
//大写转小写
for(int i = 0; i < s.size(); i++)
{
s[i] = tolower(s[i]);
}
for(int i = 0; i < t.size(); i++)
{
t[i] = tolower(t[i]);
}
int cnt = 0, first = 0;
if(t.find(s) == -1)
{
cout << -1 << endl;
}
else
{
first = t.find(s);
int pos = 0;
while(t.find(s, pos) != -1)
{
pos = t.find(s, pos);
cnt++;
pos++;
}
cout << cnt << " " << first << endl;
}
return 0;
}6.连续自然数和
题目: P1147 连续自然数和
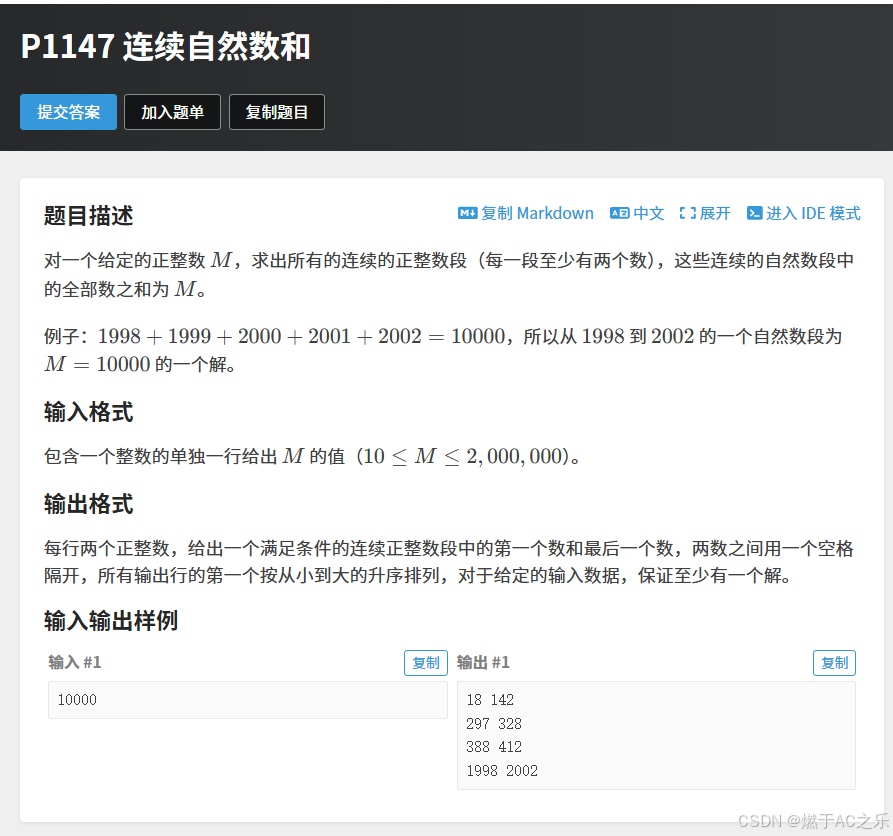
解法:前缀和 + 哈希表
对于一个连续的区间求和,首先想到前缀和进行处理,要找一个区间的值为m,那么就起始点到这点i的和sum(前缀和)➖ 前面某点j的区间和为sum - m即为m区间,注意: 对应m区间下标为 [j + 1, i] 。而要想快速知道前缀和对应的下标,可以用经典的套路 前缀和 + 哈希表 ,mp[sum] = i, 即为前缀和为sum对应的索引。
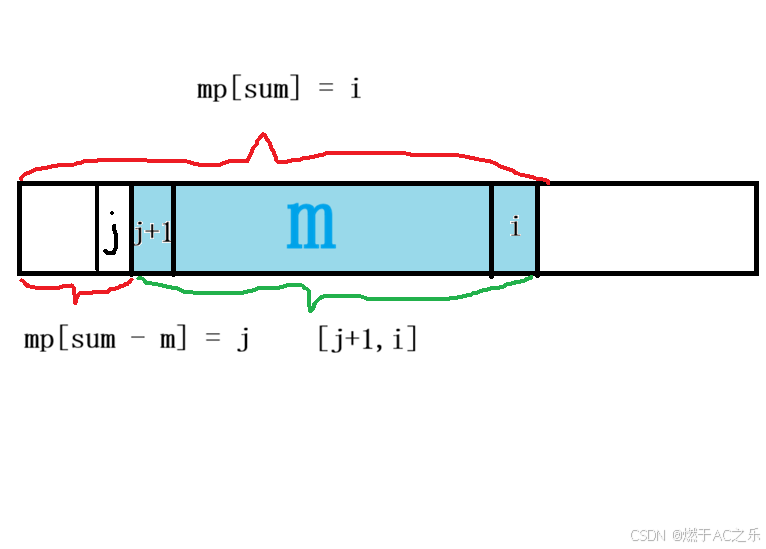
代码:
cpp
#include <iostream>
#include <unordered_map>
using namespace std;
typedef long long LL;
int m;
unordered_map<LL, int> mp; //前缀和对应的索引
int main()
{
cin >> m;
int n = (m + 1) / 2; //枚举范围
mp[0] = 0; //<0, 0> 赋值语句(执行操作)不能直接在全局作用域执行
LL sum = 0;
for(int i = 1; i <= n; i++)
{
sum += i;
//sum - m
if(mp.count(sum - m))
{
cout << mp[sum - m] + 1 << " " << i << endl;
}
mp[sum] = i;
}
return 0;
}

看到这里请点个赞,关注,如果觉得有用就收藏一下吧。后续还会持续更新的。 创作不易,还请多多支持!