Cocos Creator Shader 入门 ⒅ —— 流光动画

💡 本系列文章收录于个人专栏 ShaderMyHead。

💡 本文案例可以在 Github 上进行演示。

流光动画是游戏视觉设计中不可或缺的动态效果之一，它常见于图标强调、道具边框、UI装饰等多种场景中。

该效果通过模拟高光沿表面流动的动态变化，为原本静态的图形注入细腻的光泽感和强烈的动感表现，不仅能显著提升元素的视觉吸引力，也更易于引导玩家关注、增强界面的沉浸感：

本文将介绍如何通过 Cocos Creator 的着色器系统，来实现一些基础、有趣的流光特效。

一、线性移动流光

我们先来实现一个最常见的、线性移动的流光，它的代码比较简单：

js 复制代码

// 沿斜向线性移动的流光（简单版）
CCProgram fs-1 %{
  precision highp float;
  #include <cc-global>     // 引入 cc_time 变量
  #include <sprite-texture>

  in vec2 uv;

  uniform UBO {
    float width;       // 流光宽度（基于 UV）
    float strength;    // 流光强度（默认值 1.6）
    float speedScale;  // 流光速度系数
  };

  vec4 frag () {
    vec4 color = texture(cc_spriteTexture, uv);

    float time = cc_time.x * speedScale;  // cc_time.x 表示帧时间
    float offset = -width + mod(time, 1.0 + 2.0 * width);  // 保证偏移值循环变化

    // 判断 uv 是否在流光范围内
    if (uv.x >= offset && uv.x <= offset + width) {
      color *= strength;
    }
  }
}%

下方为代码的分析和扩展。

1.1 流光偏移计算

在上方片元着色器代码段的第 18 行，使用了 cc_time.x 来用于动画时间进程的计算，它是 Cocos Creator 着色器内置的全局变量（通过 cc-global 内置模块引入），其 x 分量表示「游戏从启动到当前的全局时间（秒）」，会从 0 开始逐步增加，因此 cc_time.x 在游戏里常用于驱动正弦摆动、帧动画插值。

第 19 行用于计算流光区域的偏移，-width 表示初始偏移量，确保流光在屏幕左边界之外开始，来达成「渐入」效果。

接着通过使用 mod 进行取余，起初 time 为 0，然后逐渐增大，取余结果也会从 0 逐步增加，来推动流光的偏移，从而达成流光不断移动的动画。

留意 mod 的第二个参数值被设定为 1.0 + 2.0 * width，一方面是为了保障取余的值可以在 UV 坐标的 [0, 1] 区间内循环变化，从而让流光不断循环扫过，一方面则是为了给流光消失到再次出现的过程，保留一些空白时间：

mod(time, 1.0)：可以保障取余结果在 [0, 1] 区间，但当流光刚扫出画布右边，就会立刻从左边跳回来，会很突兀；
mod(time, 1.0 + 2.0 * width)：提供 2.0 * width 的缓冲地带，让流光消失后，隔一会儿再出现。

1.2 流光区域检测

鉴于流光的左边界可确定为 offset，右边界为 offset + width，那么很容易判断当前像素是否落在流光区域内部：

js 复制代码

if (uv.x >= offset && uv.x <= offset + width) {
    // 当前像素落在流光区域内部
}

若是，就将当前像素的色值乘以强度系数 strength 来高亮展示，否则不做任何加工处理（返回原像素色值）。

此时执行效果如下：

1.3 为流光增加倾斜角度

为流光带上些许倾斜角度，可以显得更加自然，我们可以新增一个 lineSlope 倾斜率，来预设流光左边界的直线可以符合方程式：

js 复制代码

uv.x = lineSlope * uv.y + offset

若 lineSlope = 0，则流光没有任何倾斜；其它情况流光会随着 lineSlope 值的变化而逐步倾斜。

假设 lineSlope = -0.3，offset = 0，上述方程式可简化为 x = -0.3 * y，其图像就是一条倾斜的直线：

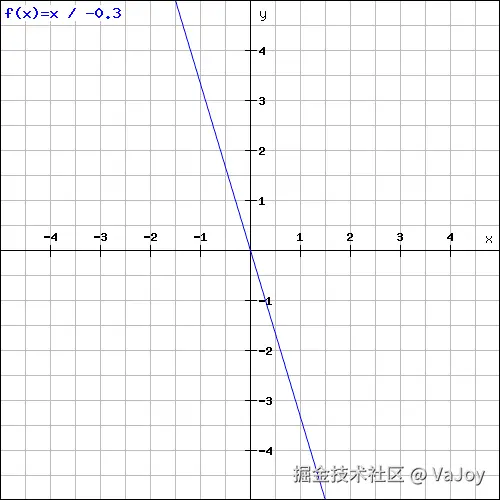
此时只要修改流光左右两侧的边界判断逻辑，便能将其倾斜化：

js 复制代码

    float lineSlope = -0.3; // 控制流光的倾斜角度

    // 判断 uv 是否在流光范围内
    if (uv.x >= lineSlope * uv.y + offset && 
        uv.x <= lineSlope * uv.y + offset + width) {
      color *= strength;
    }

此时执行效果如下：

💡 由于在 UV 坐标体系中的 y 轴是反向的（上方为 0，下方为 1），故倾斜方向会和前文的函数曲线相反。

1.4 高光线性渐变

目前的流光类似一个被实心填充的矩形，我们可以将其调整为线性渐变的高光，使其显得不会过于生硬。

对于处在流光区域的像素，我们需要获取「当前像素到流光左边界的水平距离」，计算该距离在流光宽度上的占比，最后使用 mix 函数按占比调整高光的强度即可：

js 复制代码

  // 当前像素相对于流光线的位置（在带状区域的横向偏移）
  float distanceToLine = uv.x - (lineSlope * uv.y + offset);

  // 判断是否在流光带范围内
  if (distanceToLine >= 0.0 && distanceToLine <= width) {
    // 线性渐变：右边缘=1（最亮），左边缘=0（不亮）
    float gradient = distanceToLine / width;
    color *= mix(1.0, strength, gradient);
  }

二、旋转式流光的实现

我们再来实现一个环绕着图像中心旋转的流光。

该动画方案的核心是 ------ 以图像中心为原点，构造一条旋转的向量，再用点乘计算出与当前像素的关系，形成两条对称的亮带，并随时间旋转。

我们来逐步实现相关功能。

2.1 初始化

首先我们初始化流光的方向向量和旋转角度：

js 复制代码

  uniform UBO {
    float speedScale;  // 流光旋转速度系数，默认为 0.5
  };
  
  vec4 frag () {
    vec4 baseColor = texture(cc_spriteTexture, uv);
    
    // 初始流光光照方向单位向量
    vec2 dir = normalize(vec2(1.0) - vec2(0.0));

    // 旋转角度，会随时间旋转
    float angle = fract(cc_time.x * speedScale) * 6.2831853;
  }

其中流光的向量 dir 初始化为「从右上角指向左下角」的单位向量，这里使用到了上一章光照实现的 normalize 归一化函数。

angle 表示流光的旋转角度，这里通过 fract 截取小数部分，来获取跟随时间变化，但区间又限定在 [0, 1] 内的小数。接着乘以 2π，就得到了一个在 [0, 2π] 区间内周期性变化的角度。

2.2 旋转向量

我们需要把 angle 的旋转角度应用到流光的向量 dir 上，可以通过旋转矩阵公式来处理：

js 复制代码

    float cosA = cos(angle);
    float sinA = sin(angle);
    dir = vec2(dir.x * cosA - dir.y * sinA,
              dir.x * sinA + dir.y * cosA);

这样 dir 就是绕中心旋转了 angle 角度后的向量。

💡 二维旋转矩阵公式明确了 ------ 对于一个二维向量 (x, y)，绕原点旋转角度 θ 后的新向量是：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> [ x ′ y ′ ] = [ cos ⁡ θ − sin ⁡ θ sin ⁡ θ cos ⁡ θ ] ⋅ [ x y ] \begin{bmatrix} x' \\ y' \end{bmatrix} = \begin{bmatrix} \cos\theta & -\sin\theta \\ \sin\theta & \cos\theta \end{bmatrix} \cdot \begin{bmatrix} x \\ y \end{bmatrix} </math>[x′y′]=[cosθsinθ−sinθcosθ]⋅[xy]

等价于：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> x ′ = x ⋅ cos ⁡ θ − y ⋅ sin ⁡ θ x' = x \cdot \cos\theta - y \cdot \sin\theta </math>x′=x⋅cosθ−y⋅sinθ
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> y ′ = x ⋅ sin ⁡ θ + y ⋅ cos ⁡ θ y' = x \cdot \sin\theta + y \cdot \cos\theta </math>y′=x⋅sinθ+y⋅cosθ

2.3 计算亮度并混合颜色

我们需要判断每个像素点相对于中心点的位置，从而计算流光的强度：

js 复制代码

    // 当前像素点相对中心的向量
    vec2 offset = uv - vec2(0.5);

    // 点积计算当前像素在流光方向上的投影
    float glow = abs(dot(offset, dir));

其中我们使用了 dot(offset, dir) 来计算出 offset 在 dir 向量上的投影长度：

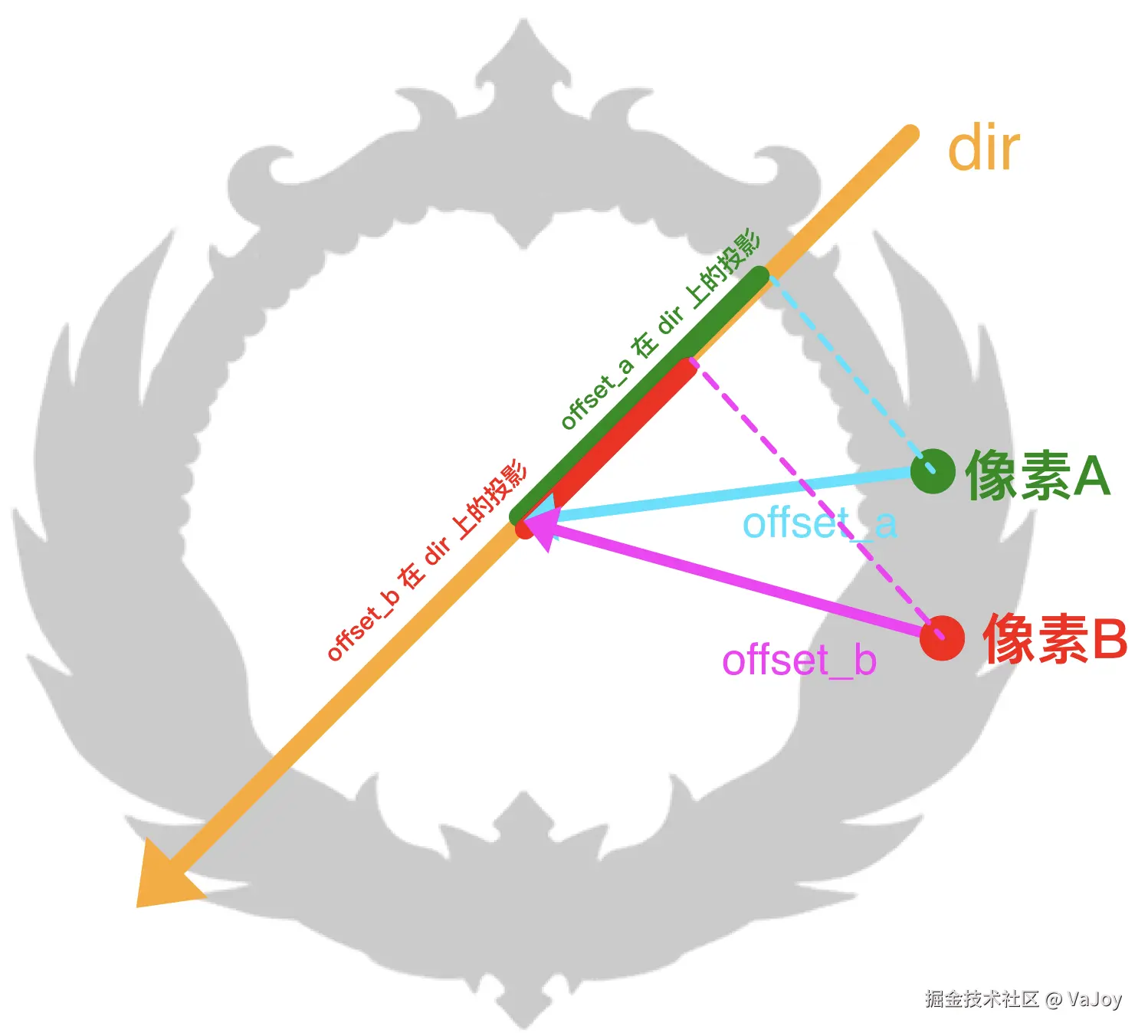
可以看到当 offset 向量方向与流光的光照方向更贴近时，投影的长度会更长（该像素应显示得更亮）。

另外鉴于 dir 是归一化后的单位向量（长度为 1），从上图可以得知投影长度 glow 的区间会在 [0, 0.5] 之间。

最后我们把 glow 当做高光的强度，来进一步计算获得高光，并叠加上原像素色值：

js 复制代码

    vec2 offset = uv - vec2(0.5);
    float glow = abs(dot(offset, dir));

    // 避免透明区域发光
    glow *= baseColor.a;

    // 叠加强度
    vec4 glowColor = baseColor * glow;

    return baseColor + glowColor;

此时执行效果为：

2.4 聚拢高光

虽然我们已实现了旋转的流光动画，但目前高光的覆盖范围较大，且明暗过渡过于平滑（流光太松散）。

对此我们可以使用指数函数 pow 来聚拢高光：

js 复制代码

    float glow = abs(dot(offset, dir));
    glow *= baseColor.a;  

    // 新增，聚拢流光
    glow = pow(glow, 2.0); 

    vec4 glowColor = baseColor * glow;
    return baseColor + glowColor;

指数函数会压缩较小的值、放大较大的值，进而让光带中心更亮、边缘更暗：

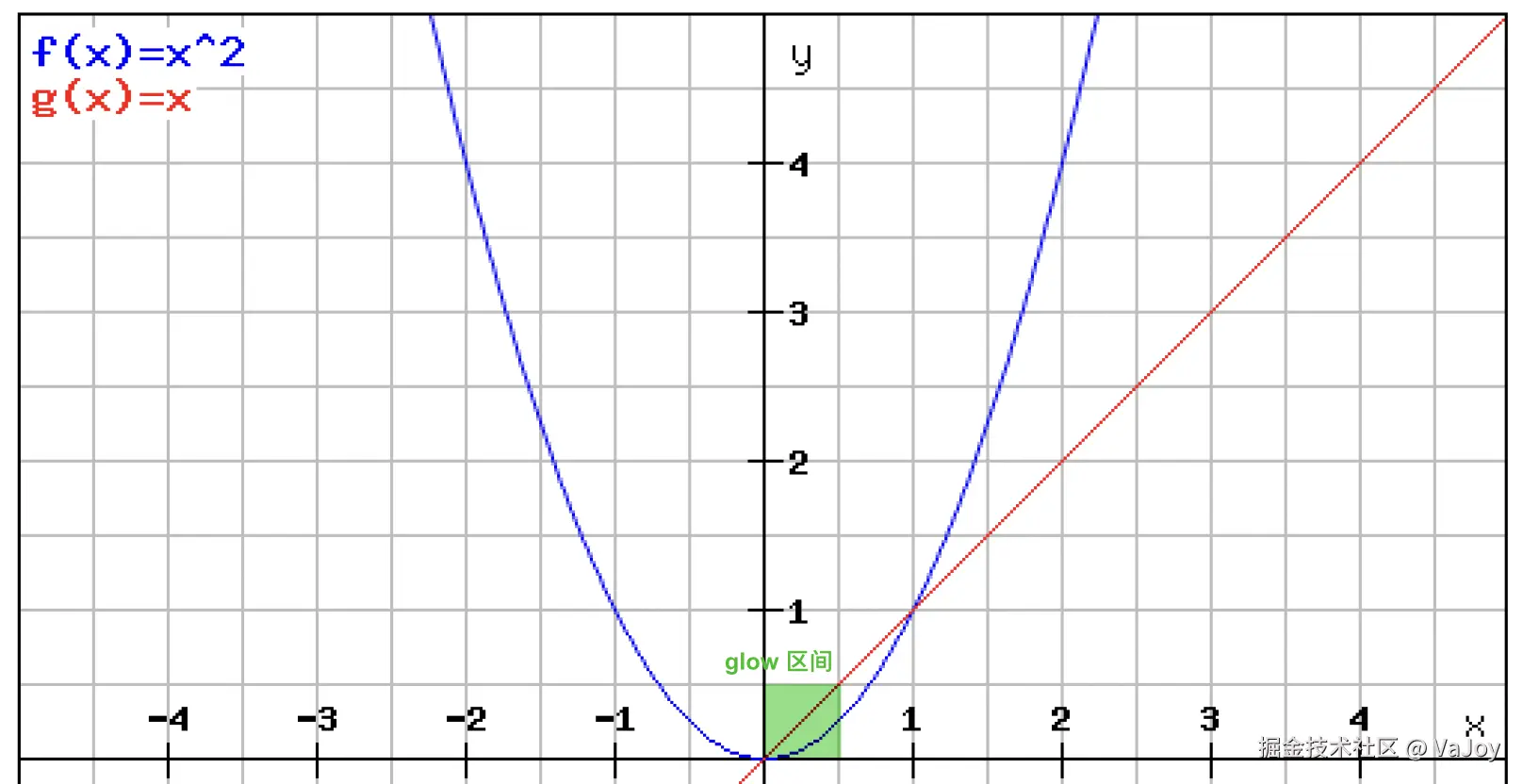
但该函数也将 glow 区间从原本的 [0, 0.5] 压缩到了 [0, 0.25]，会导致整体的光效变暗。我们可以再多加一个流光强度系数来放大整体光效：

js 复制代码

  uniform UBO {
    float strength;    // 新增流光强度系数，默认为 9.0
    float speedScale;
  };
  
  vec4 frag () {
    // 略...
      
    glow = pow(glow, 2.0); 

    // 使用 strength 强化整体亮度
    vec4 glowColor = baseColor * glow * strength;
    return baseColor + glowColor;
  }

当前执行效果如下（此处 strength 值为 9.0，会呈现非常明亮的高光）：

三、水波纹式流光

我们在文章最后来实现一个更高级的水波纹式流光，其核心是通过一种迭代噪声函数，在纹理的 UV 空间上生成动态的、环状的、相互干涉的波纹，并根据波纹的强度来增强原始纹理的亮度，从而模拟出光线在水波或能量场中流动、散射的效果。

其完整的片元着色器代码如下：

js 复制代码

CCProgram fs-3 %{
  precision highp float;
  #include <cc-global>
  #include <sprite-texture>

  in vec2 uv;

  uniform RippleUBO {
    float rippleDensity; // 水波纹密度，默认为 16.0。值越大，UV 空间被缩放得越小，产生的波纹数量就越密集
  };

  #pragma define iterationCount 3 // 迭代次数，越大越复杂

  vec4 frag () {
    vec4 baseColor = texture(cc_spriteTexture, uv);

    float time = cc_time.x * 0.5;

    // 将 UV 坐标放大到波纹密度空间，再通过 mod 保证循环，并减去 250.0 作为偏移。
    // 减去 250 是为了将坐标中心偏移到一个非常大的负值区域，从而在后续的三角函数计算中产生更剧烈、更不可预测的变化。
    vec2 p = mod(uv * rippleDensity, rippleDensity) - 250.0;
    vec2 i = p;

    float accum = 1.0;  // 累积的波动值
    float intensity = 0.0045;  // 波纹的振幅控制，值越大，波动越明显。

    // 多次迭代叠加波动效果
    // 让原始坐标 p 在三角函数扰动下不断变化，从而产生水波流动感
    for (int n = 0; n < iterationCount; n++) {
        // 每次迭代的时间缩放不同，使得不同频率波纹错开，形成复杂波动。
        float t = time * (1.0 - (3.5 / float(n+1)));

        // 更新迭代向量，使用三角函数生成复杂的扰动
        i = p + vec2(
          cos(t - i.x) + sin(t + i.y),
          sin(t - i.y) + cos(1.5*t + i.x)
        );

        // 将扰动累加到 accum，并用倒数加强波峰
        accum += 1.0 / length(vec2(
          p.x / (cos(i.x + t) / intensity),
          p.y / (cos(i.y + t) / intensity)
        ));
    }

    accum /= 5.0;                    // 归一化累积值
    accum = 1.17 - pow(accum, 1.4);  // 让波峰更尖锐，波谷更平滑，视觉上更像水波光斑

    vec3 rippleColor = vec3(pow(abs(accum), 20.0));      // 让波峰更尖锐，波谷更平滑，视觉上更像水波光斑
    rippleColor = clamp(rippleColor, 0.0, baseColor.a);

    // 波光与原始颜色混合
    vec3 finalRGB = baseColor.rgb + rippleColor * accum;
    return vec4(finalRGB, baseColor.a);
  }
}%

本案例的实现趋于公式化和复杂，因此不做过多烧脑的分析，读者若有兴趣可自行阅读注解和研究。

执行效果如下：

留意我们在代码段第 21 行，先通过 uv * rippleDensity 将 UV 放大 rippleDensity 倍，再通过 mod 函数对放大后的 UV 取余，使其值始终在 [0, rippleDensity] 之间循环。

这相当于把原始纹理「分割」成了 rippleDensity x rippleDensity 个重复的格子，因此通过调大 rippleDensity 的数值，可以得到更多的格子，进而看到更多的纹理：

💡 可以在线上演示页面体验本文案例的更多动画细节。