Carrier Aggregation Enabled MIMO-OFDM Integrated Sensing and Communication

文章目录

• • • [C. Sensing Mode](#C. Sensing Mode)
  • [II. A NOVEL CA-ENABLED MIMO-OFDM ISAC SIGNAL PROCESSING METHOD](#II. A NOVEL CA-ENABLED MIMO-OFDM ISAC SIGNAL PROCESSING METHOD)
  • • [A. Signal Preprocessing Stage](#A. Signal Preprocessing Stage)
    • [B. Sensing Performance Analysis](#B. Sensing Performance Analysis)

对支持 CA 的 ISAC 系统的研究可分为两类：带内 CA 和带间 CA。支持 CA 的 ISAC 系统的主要挑战在于信号设计和处理。相关工作的总结如表 I 所示，详情如下。

• Intra-band CA：为带内 CA 设计了两种主要的 ISAC 信号：步进载波 OFDM ISAC 信号和非连续 (non-continuous，NC) 碎片化 OFDM ISAC 信号。

  • 在步进载波 OFDM ISAC 信号方面，Pfeffer 等人 [12] 提出了步进载波 OFDM 信号的概念，该概念在连续的 OFDM 符号周期内为每个资源块组分配不同的载波频率，从而扩展了总带宽并增强了感知性能。然而，它未能考虑到由快速移动目标引起的多普勒频移。 为此，Schweizer 等人 [13] 探索了一种改进的 DFT 方法，以减轻步进载波 OFDM 方案中由目标高移动性引起的相位误差，从而获得高精度的速度估计。
  • 在非连续 (NC) 碎片化 OFDM ISAC 信号方面，Huang 等人 [14] 介绍了一种 NC 碎片化 OFDM ISAC 系统，该系统可以灵活分配频谱带并适应动态频谱环境。然而，缺失的频谱带会恶化目标感知中的傅里叶旁瓣。为解决此问题，Liu 等人 [15] 提出了一种针对碎片化频谱带的感知方法，该方法利用压缩感知 (CS) 和机器学习来实现具有低旁瓣的高精度距离和速度估计。

• Inter-band CA：多波段雷达是带间 CA 的一个代表性例子。Cuomo 在 [16] 中讨论了一种非连续多波段相干雷达，并提出了一种带宽外推 (BWE) 方法来恢复缺失的频谱带，从而提高雷达的距离分辨率。Suwa 等人 [17] 将 BWE 方法扩展到极化雷达，实现了高分辨率的距离估计。

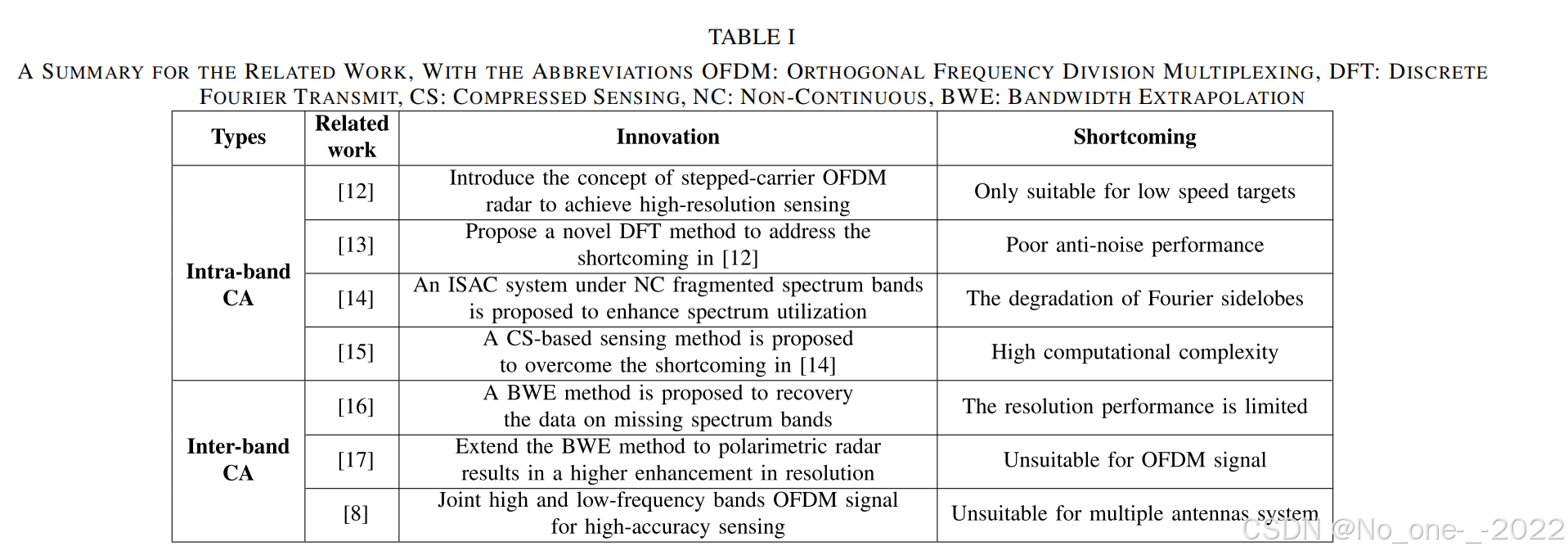
总而言之，带内和带间 CA 提升了碎片化频带的有效利用率，从而在通信和感知两方面都带来了性能增益。目前，移动通信系统中的碎片化频带大多是分散的，这表明带间 CA 在移动通信系统中有更广泛的应用。然而，对于 ISAC 移动通信系统中带间 CA 的研究却非常稀少。在我们之前的工作中，我们研究了支持 CA 的 OFDM ISAC 系统，并通过验证 [8] 证实了 CA 的有效性。然而，我们最初的探索虽然有价值，但在一定程度上仍是初步和理想化的，忽略了移动通信系统中典型的 MIMO-OFDM 信号以及由实际信道环境引起的感知信号处理挑战。因此，进一步研究支持 inter-band CA-enabled ISAC 信号处理的可行性和实用性尤为关键。

因此，本文研究了一种支持 CA 的 MIMO-OFDM ISAC 系统，其中碎片化的高频和低频频带被共享用于下行链路 (DL) 通信和感知潜在目标。此外，本文还提出了一种支持 CA 的 MIMO-OFDM ISAC 信号模型及相应的感知处理方法。通过理论推导和数值仿真，我们验证了所提出的 ISAC 系统相对于传统 ISAC 系统的优越性。本文的主要贡献总结如下。

• 我们提出了一种支持 CA 的 MIMO-OFDM ISAC 系统，旨在实现无与伦比的通信体验和高精度感知。通过引入 CA 和 MIMO，ISAC 系统的通信容量得到显著增强，同时也提高了感知的准确度和抗噪声能力。仿真结果验证了所提出的 ISAC 系统的可行性和效率，展示了其相对于传统 ISAC 系统的优势。

• 在感知信号处理方面，我们研究了高低频段感知数据的数据级和符号级融合。

  • 数据级融合指的是对感知数据估计出的多目标信息进行融合，
  • 符号级融合则指的是对接收到的带有相位信息的符号进行融合 [18], [19]。

在感知数据的符号级融合中，存在两个挑战：1) 由于衰减和雷达截面 (RCS) 的影响，高低频段回波信号的初始相位存在失准；2) 具有不同物理层参数的高低频段感知数据的融合。

• 为此，本文将感知信号处理分解为 信号预处理阶段 和 感知信息融合 阶段。

  • 信号预处理阶段充分利用来自多个天线的感知数据，同时使用循环互相关 (CCC) 方法对齐高低频段回波信号的初始相位，具体如 III-A 节所述。
  • 在感知信息融合阶段，本文通过重排高低频特征向量，并利用循环前缀 (CP) 动态调整的前提，实现了高低频段感知数据的符号级融合以及对目标距离和速度的估计，具体如 III-B 节所述。

C. Sensing Mode

为了更好地反映实际场景，我们考虑了在感知信号处理中直接或间接影响高低频聚合的因素，包括由 衰减差异 、物理参数变化 和 噪声方差差异 引起的相位对齐误差 [31]。据我们所知，这是支持 CA 的 ISAC 研究中首次考虑相位对齐误差和噪声方差差异的工作，使其更适用于实际应用。

1. 感知信道模型 ：我们假设第 i i i 个潜在目标的径向速度为 v i , 0 v_{i,0} vi,0，与基站的距离为 r i , 0 r_{i,0} ri,0。同时，第 i i i 个目标与基站之间的到达角 (AoA) 和离开角 (AoD) 相同，表示为 θ i , Rx = θ i , Tx \theta_{i,\text{Rx}} = \theta_{i,\text{Tx}} θi,Rx=θi,Tx。发射和接收导向矢量分别如 (9) 和 (10) 所示。

a Rx ( θ i , Rx ) = [ e j 2 π p ( d r λ b ) sin ⁡ ( θ i , Rx ) ] p = 0 , 1 , ⋯   , N R − 1 T (9) \mathbf{a}{\text{Rx}}(\theta{i,\text{Rx}}) = \left[ e^{j2\pi p(\frac{d_r}{\lambda^b})\sin(\theta_{i,\text{Rx}})} \right]_{\ p=0,1,\cdots,N_R-1}^{\text{T}} \tag{9} aRx(θi,Rx)=[ej2πp(λbdr)sin(θi,Rx)] p=0,1,⋯,NR−1T(9)

a Tx ( θ i , Tx ) = [ e j 2 π k ( d t λ b ) sin ⁡ ( θ i , Tx ) ] k = 0 , 1 , ⋯   , N T − 1 (10) \mathbf{a}{\text{Tx}}(\theta{i,\text{Tx}}) = \left[ e^{j2\pi k(\frac{d_t}{\lambda^b})\sin(\theta_{i,\text{Tx}})} \right]_{\ k=0,1,\cdots,N_T-1} \tag{10} aTx(θi,Tx)=[ej2πk(λbdt)sin(θi,Tx)] k=0,1,⋯,NT−1(10)

其中 p p p 表示基站接收天线的索引； λ b = c / f c b \lambda^b = c/f_c^b λb=c/fcb 是波长，其中 c c c 是光速。在第 m m m 个 OFDM 符号时间内，第 n n n 个子载波上，第 b b b 个 CC 的感知信道模型表示为 [29] 和 [32]

H m , n b = ∑ i = 1 I [ κ i , S b e j 2 π ( f i , S b m T b − n Δ f b τ i , 0 ) a Rx ( θ i , Rx ) a Tx T ( θ i , Tx ) ] (11) \mathbf{H}{m,n}^b = \sum{i=1}^{I} \left[ \kappa_{i,S}^b e^{j2\pi(f_{i,S}^b m T^b - n \Delta f^b \tau_{i,0})} \mathbf{a}{\text{Rx}}(\theta{i,\text{Rx}})\mathbf{a}{\text{Tx}}^{\text{T}}(\theta{i,\text{Tx}})\right] \tag{11} Hm,nb=i=1∑I[κi,Sbej2π(fi,SbmTb−nΔfbτi,0)aRx(θi,Rx)aTxT(θi,Tx)](11)

其中 H m , n b ∈ C N R × N T \mathbf{H}{m,n}^b \in \mathbb{C}^{N_R \times N_T} Hm,nb∈CNR×NT， κ i , S b = ( λ b ) 2 ( 4 π ) 3 r i , 0 4 β i , S b \kappa{i,S}^b = \sqrt{\frac{(\lambda^b)^2}{(4\pi)^3 r_{i,0}^4}} \beta_{i,S}^b κi,Sb=(4π)3ri,04(λb)2 βi,Sb 是第 i i i 个目标与基站之间的衰减，其中 β i , S b ∼ C N ( 0 , σ β , S 2 ) \beta_{i,S}^b \sim \mathcal{CN}(0, \sigma_{\beta,S}^2) βi,Sb∼CN(0,σβ,S2) 是第 i i i 个目标的雷达截面 (RCS) [33]，它表征了高低频段初始相位的差异； f i , S b = 2 f c b v i , 0 c f_{i,S}^b = \frac{2f_c^b v_{i,0}}{c} fi,Sb=c2fcbvi,0 和 τ i , 0 = 2 r i , 0 c \tau_{i,0} = \frac{2r_{i,0}}{c} τi,0=c2ri,0 分别是多普勒频移和延迟。

2. 接收感知信号 ：[34] 验证了高频和低频段信号具有相似的行为，即它们通过相同的视距路径和目标反射到达基站的接收机 (Rx)。在基站的接收端，混合的高低频段感知回波信号通过匹配滤波被分离。因此，在第 m m m 个 OFDM 符号时间内，第 n n n 个子载波上接收到的回波信号表示为

y m , n S = ∑ b = 1 B y m , n S , b = ∑ b = 1 B H m , n b w Tx b d m , n b + z m , n S , b (12) \mathbf{y}{m,n}^S = \sum{b=1}^{B} \mathbf{y}{m,n}^{S,b} = \sum{b=1}^{B} \mathbf{H}{m,n}^b \mathbf{w}{\text{Tx}}^b d_{m,n}^b + \mathbf{z}_{m,n}^{S,b} \tag{12} ym,nS=b=1∑Bym,nS,b=b=1∑BHm,nbwTxbdm,nb+zm,nS,b(12)

其中 y m , n S ∈ C N R × 1 \mathbf{y}{m,n}^S \in \mathbb{C}^{N_R \times 1} ym,nS∈CNR×1 且 y m , n S , b \mathbf{y}{m,n}^{S,b} ym,nS,b 表示第 b b b 个 CC 中的回波信号； W Tx b ∈ C N T × N T \mathbf{W}_{\text{Tx}}^b \in \mathbb{C}^{N_T \times N_T} WTxb∈CNT×NT 表示发射波束成形

II. A NOVEL CA-ENABLED MIMO-OFDM ISAC SIGNAL PROCESSING METHOD

本节中，我们提出了一种新颖的支持 CA 的 MIMO-OFDM ISAC 信号处理方法，如图 2 所示。不失一般性，我们假设第一个 CC 在低频段，第二个 CC 在高频段。通过接收端的匹配滤波，两个 CC 上的混合感知回波信号被分离。

在所提出的 ISAC 系统中，感知信号处理存在两个挑战：1) 由于衰减和 RCS，高低频段回波信号的初始相位失准；2) 具有不同物理层参数（如子载波间隔和符号时长）的高低频段感知数据的融合。因此，我们考虑了高低频段感知数据的数据级和符号级融合方法。

数据级融合方法如下：在高低频段的混合回波信号分离后，将 [35] 中提出的联合角度-距离-速度估计算法应用于高频段的回波信号，以获得估计的距离集 { r i , data 1 } i = 1 , 2 , ⋯   , I \{r^1_{i,\text{data}}\}{i=1,2,\cdots,I} {ri,data1}i=1,2,⋯,I 和速度集 { v i , data 1 } i = 1 , 2 , ⋯   , I \{v^1{i,\text{data}}\}{i=1,2,\cdots,I} {vi,data1}i=1,2,⋯,I，这些目标具有一一对应的关系。类似地，通过处理低频段的回波信号，可以得到估计的距离集 { r i , data 2 } i = 1 , 2 , ⋯   , I \{r^2{i,\text{data}}\}{i=1,2,\cdots,I} {ri,data2}i=1,2,⋯,I 和速度集 { v i , data 2 } i = 1 , 2 , ⋯   , I \{v^2{i,\text{data}}\}_{i=1,2,\cdots,I} {vi,data2}i=1,2,⋯,I。

我们结合精度差异来给出数据级融合权重 [36]，并且接收信号在高低频段的方差可以通过一些方法获得，例如最大似然估计 (MLE) [37]。因此，第 i i i 个目标的距离最终估计为

r ^ i , data = r i , data 1 + σ S , 1 2 Δ f 2 M b σ S , 1 2 Δ f 2 M b + σ S , 2 2 Δ f 1 M b ( r i , data 2 − r i , data 1 ) \hat{r}{i,\text{data}} = r^1{i,\text{data}} + \frac{\sigma^2_{S,1}\Delta f^2 M_b}{\sigma^2_{S,1}\Delta f^2 M_b + \sigma^2_{S,2}\Delta f^1 M_b} (r^2_{i,\text{data}} - r^1_{i,\text{data}}) r^i,data=ri,data1+σS,12Δf2Mb+σS,22Δf1MbσS,12Δf2Mb(ri,data2−ri,data1)

，而第 i i i 个目标的速度最终估计为

v ^ i , data = v i , data 1 + σ S , 1 2 Δ f 2 N b σ S , 1 2 Δ f 2 N b + σ S , 2 2 Δ f 1 ( v i , data 2 − v i , data 1 ) \hat{v}{i,\text{data}} = v^1{i,\text{data}} + \frac{\sigma^2_{S,1}\Delta f^2 N_b}{\sigma^2_{S,1}\Delta f^2 N_b + \sigma^2_{S,2}\Delta f^1} (v^2_{i,\text{data}} - v^1_{i,\text{data}}) v^i,data=vi,data1+σS,12Δf2Nb+σS,22Δf1σS,12Δf2Nb(vi,data2−vi,data1)

29\]。然而，数据级融合方法产生的感知精度有限。因此，本文提出了一种两阶段的符号级融合方法，包括信号预处理阶段和感知信息融合阶段，详见 III-A 节。 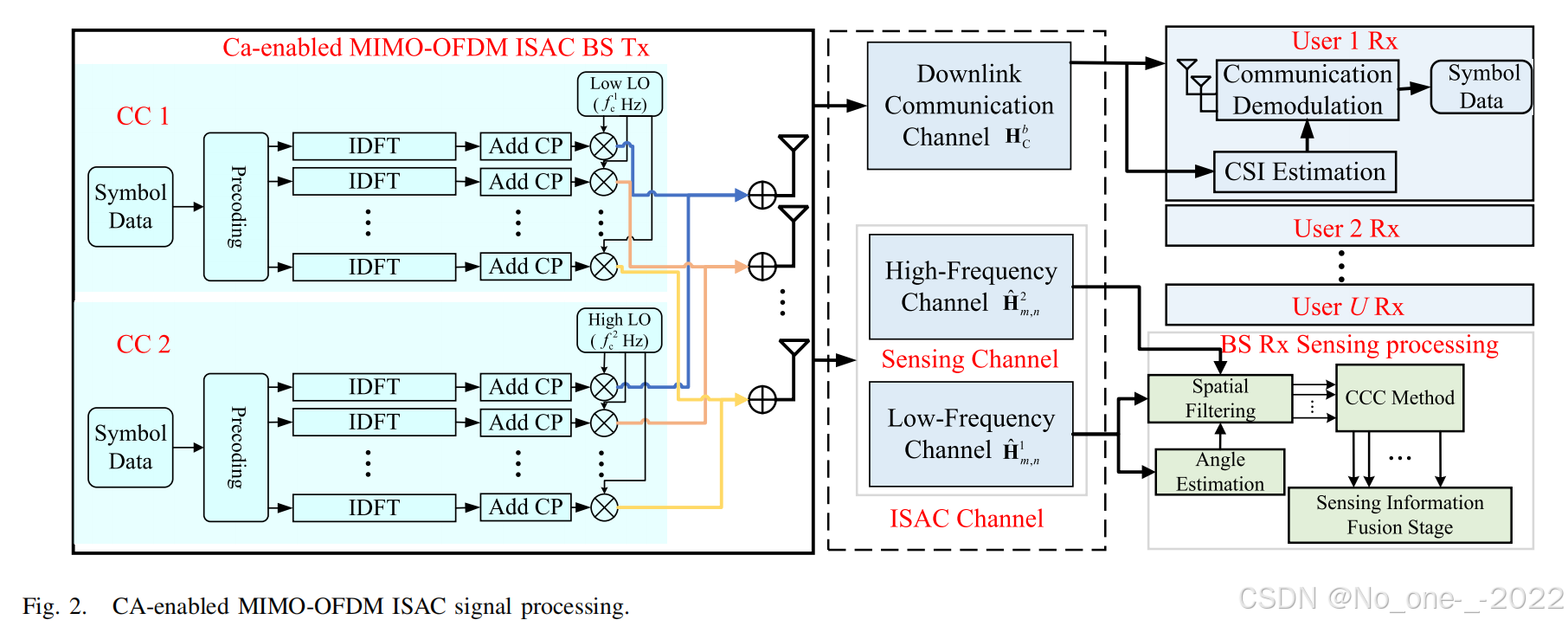 #### A. Signal Preprocessing Stage 感知预处理的主要目的之一是对齐高低频段回波信号的初始相位。 1. **角度估计**：由于两个 CC 具有相同的 AoA 和 AoD，并且低频段回波信号的信噪比 (SNR) 很高，我们利用低频段的回波信号来估计 AoA。 首先，我们通过右乘广义逆矩阵 X m , n † = ( d m , n 1 ) H ( d m , n 1 ( d m , n 1 ) H + ϱ I ) − 1 \\mathbf{X}_{m,n}\^{\\dagger} = (\\mathbf{d}_{m,n}\^1)\^H (\\mathbf{d}_{m,n}\^1 (\\mathbf{d}_{m,n}\^1)\^H + \\varrho \\mathbf{I})\^{-1} Xm,n†=(dm,n1)H(dm,n1(dm,n1)H+ϱI)−1 来消除 y m , n S , 1 \\mathbf{y}_{m,n}\^{S,1} ym,nS,1 中已知的发射数据 d m , n 1 \\mathbf{d}_{m,n}\^1 dm,n1，所有天线接收到的低频段回波信号为 H \^ m , n 1 = y m , n S , 1 X m , n † ≈ ∑ i = 1 I \[ κ i , S 1 e j 2 π ( f i , S 1 m T 1 − n Δ f 1 τ i , 0 ) a Rx ( θ i , Rx ) a Tx T ( θ i , Tx ) I \] W Tx b + z m , n S , 1 X m , n † (13) \\hat{\\mathbf{H}}_{m,n}\^1 = \\mathbf{y}_{m,n}\^{S,1} \\mathbf{X}_{m,n}\^{\\dagger} \\approx \\sum_{i=1}\^{I} \\left\[ \\kappa_{i,S}\^1 e\^{j2\\pi(f_{i,S}\^1 m T\^1 - n \\Delta f\^1 \\tau_{i,0})} \\mathbf{a}_{\\text{Rx}}(\\theta_{i,\\text{Rx}})\\mathbf{a}_{\\text{Tx}}\^{\\text{T}}(\\theta_{i,\\text{Tx}})\\mathbf{I} \\right\] \\mathbf{W}_{\\text{Tx}}\^b + \\mathbf{z}_{m,n}\^{S,1}\\mathbf{X}_{m,n}\^{\\dagger} \\tag{13} H\^m,n1=ym,nS,1Xm,n†≈i=1∑I\[κi,S1ej2π(fi,S1mT1−nΔf1τi,0)aRx(θi,Rx)aTxT(θi,Tx)I\]WTxb+zm,nS,1Xm,n†(13) 其中 H \^ m , n 1 ∈ C N R × N T \\hat{\\mathbf{H}}_{m,n}\^1 \\in \\mathbb{C}\^{N_R \\times N_T} H\^m,n1∈CNR×NT 且 I ∈ C N T × N T \\mathbf{I} \\in \\mathbb{C}\^{N_T \\times N_T} I∈CNT×NT 是单位矩阵。 ϱ \\varrho ϱ 表示为提高数值恢复精度而引入的正则化参数 \[19\]。 通过观察 H \^ m , n 1 \\hat{\\mathbf{H}}_{m,n}\^1 H\^m,n1，可以明显看出 AoA 在接收天线阵元上引入了线性相移。AoA 的估计可以通过多重信号分类 (MUSIC) 方法、基于旋转不变技术的信号参数估计方法以及基于复数神经网络的先进方法 \[3\], \[38\] 获得。由于 MUSIC 方法能够高精度地实现时空频码域非连续信号的参数估计，我们以该方法为例进行说明 \[29\], \[39\]，具体步骤如下。 * **步骤 1** ：计算 H \^ m , n 1 \\mathbf{\\hat{H}}_{m,n}\^1 H\^m,n1 的协方差矩阵 R H m , n 1 \\mathbf{R}_{\\mathbf{H}_{m,n}\^1} RHm,n1。 R H \^ m , n 1 = H \^ m , n 1 \[ H \^ m , n 1 \] H N 1 M 1 ∈ C N R × N R (14) \\mathbf{R}_{\\mathbf{\\hat{H}}_{m,n}\^1} = \\frac{\\mathbf{\\hat{H}}_{m,n}\^1 \\left\[\\mathbf{\\hat{H}}_{m,n}\^1\\right\]\^{\\text{H}}}{N_1 M_1} \\in \\mathbb{C}\^{N_R \\times N_R} \\tag{14} RH\^m,n1=N1M1H\^m,n1\[H\^m,n1\]H∈CNR×NR(14) * **步骤 2** ：对 R H \^ m , n 1 \\mathbf{R}_{\\mathbf{\\hat{H}}_{m,n}\^1} RH\^m,n1 执行特征值分解 `eig(·)` 以获得 eig ( R H \^ m , n 1 ) = \[ U s , Λ s \] (15) \\text{eig}\\left(\\mathbf{R}_{\\mathbf{\\hat{H}}_{m,n}\^1}\\right) = \[\\mathbf{U}_s, \\mathbf{\\Lambda}_s\] \\tag{15} eig(RH\^m,n1)=\[Us,Λs\](15) 其中 Λ s \\mathbf{\\Lambda_s} Λs 表示一个特征值按降序排列的对角矩阵。 U s \\mathbf{U_s} Us 是正交特征矩阵。通过估计从信号矩阵的特征值得出的微分向量（differential vector）的秩，可以准确确定入射信号的数量 \[40\]，该数量被假定为与目标数量相同。然后，获得噪声子空间 U n = \[ U s \] : , I + 1 : N R \\mathbf{U_n} = \[\\mathbf{U_s}\]_{:,I+1:N_R} Un=\[Us\]:,I+1:NR，用于计算空间谱函数。 * **步骤 3** ：生成 MUSIC 空间谱向量如下 f music ( θ ) = 1 a ( θ ) H U n U n H a ( θ ) (16) f_{\\text{music}}(\\theta) = \\frac{1}{\\mathbf{a}(\\theta)\^{\\text{H}}\\mathbf{U}_n\\mathbf{U}_n\^{\\text{H}}\\mathbf{a}(\\theta)} \\tag{16} fmusic(θ)=a(θ)HUnUnHa(θ)1(16) 其中 θ ∈ ( 0 , π \] \\theta \\in (0, \\pi\] θ∈(0,π\] 且 a ( θ ) = \[ e j 2 π p ( d r λ 1 ) sin ⁡ ( θ ) \] p = 0 , 1 , ⋯   , N R − 1 T (17) \\mathbf{a}(\\theta) = \\left\[ e\^{j2\\pi p (\\frac{d_r}{\\lambda\^1}) \\sin(\\theta)} \\right\]_{\\ p=0,1,\\cdots,N_R-1}\^{\\text{T}} \\tag{17} a(θ)=\[ej2πp(λ1dr)sin(θ)\] p=0,1,⋯,NR−1T(17) * **步骤 4** ：搜索 f music f_{\\text{music}} fmusic 的 I I I 个峰值以获得 AoA 估计集 { θ \^ i ′ , Rx } i ′ = 1 , 2 , ⋯   , I \\{\\hat{\\theta}_{i', \\text{Rx}}\\}_{i'=1,2,\\cdots,I} {θ\^i′,Rx}i′=1,2,⋯,I。 *** ** * ** *** 2. **空间滤波**：为了减轻由潜在的非线性处理引入的目标重影，我们采用空间滤波操作来分离由多个目标混合而成的回波信号。 与 (13) 类似，在移除已知发射数据 d m , n b \\mathbf{d}_{m,n}\^b dm,nb 后，在第 b b b 个 CC 中，第 m m m 个 OFDM 符号时间内，第 n n n 个子载波上所有天线的回波信号表示为 H \^ m , n b ≈ ∑ i = 1 I \[ κ i , S b e j 2 π ( f i , S b m T b − n Δ f b τ i , 0 ) a Rx ( θ i , Rx ) a Tx T ( θ i , Tx ) I \] W Tx b + Z m , n S , b , (18) \\hat{\\mathbf{H}}_{m,n}\^b \\approx \\sum_{i=1}\^{I} \\left\[ \\kappa_{i,S}\^b e\^{j2\\pi(f_{i,S}\^b m T\^b - n \\Delta f\^b \\tau_{i,0})} \\mathbf{a}_{\\text{Rx}}(\\theta_{i,\\text{Rx}})\\mathbf{a}_{\\text{Tx}}\^{\\text{T}}(\\theta_{i,\\text{Tx}})\\mathbf{I} \\right\] \\mathbf{W}_{\\text{Tx}}\^b + \\mathbf{Z}_{m,n}\^{S,b}, \\tag{18} H\^m,nb≈i=1∑I\[κi,Sbej2π(fi,SbmTb−nΔfbτi,0)aRx(θi,Rx)aTxT(θi,Tx)I\]WTxb+Zm,nS,b,(18) 其中 Z m , n S , b \\mathbf{Z}_{m,n}\^{S,b} Zm,nS,b 是一个噪声矩阵。 与 OFDM 信号解调的原理类似，我们可以利用估计出的 AoA 集合 { θ \^ i ′ , Rx } i ′ = 1 , 2 , ⋯   , I \\{\\hat{\\theta}_{i',\\text{Rx}}\\}_{i'=1,2,\\cdots,I} {θ\^i′,Rx}i′=1,2,⋯,I 从 H \^ m , n b \\hat{\\mathbf{H}}_{m,n}\^b H\^m,nb 中分离出每个目标的独立回波信号。在第 b b b 个 CC 中，第 m m m 个 OFDM 符号时间内，第 n n n 个子载波上，第 i ′ i' i′ 个目标的回波信号由 (19) 表示，如后页底部所示。当目标角度差大于天线的角分辨率且信噪比不差时，**项 1** 的幅度远大于 **项 2** 的幅度。幸运的是，空间滤波操作可以在空域中带来显著的信噪比增益。 H \^ m , n b , i ′ = a Rx H ( θ \^ i ′ , Rx ) H \^ m , n b ( W Tx b ) H a Tx ∗ ( θ \^ i ′ , Tx ) / ( N R N T ) ≈ κ i ′ , S b e j 2 π ( f i ′ , S b m T b − n Δ f b τ i ′ , 0 ) ⏟ The i ′ -th target (Term 1) + a Rx H ( θ \^ i ′ , Rx ) \[ ∑ i = 1 , i ≠ i ′ I \[ κ i , S b e j 2 π ( f i , S b m T b − n Δ f b τ i , 0 ) a Rx ( θ i , Rx ) a Tx T ( θ i , Tx ) I \] W Tx b + Z m , n S , b \] ( W Tx b ) H a Tx ∗ ( θ \^ i ′ , Tx ) / ( N R N T ) ⏟ Interference (Term 2) (19) \\begin{aligned} \\hat{\\mathbf{H}}_{m,n}\^{b,i'} \& = \\mathbf{a}_{\\text{Rx}}\^{\\text{H}}(\\hat{\\theta}_{i',\\text{Rx}})\\hat{\\mathbf{H}}_{m,n}\^b (\\mathbf{W}_{\\text{Tx}}\^b)\^H \\mathbf{a}_{\\text{Tx}}\^\*(\\hat{\\theta}_{i',\\text{Tx}})/(N_R N_T) \\\\ \& \\approx \\underbrace{ \\kappa_{i',S}\^b e\^{j2\\pi(f_{i',S}\^b m T\^b - n \\Delta f\^b \\tau_{i',0})} }_{\\text{The } i'\\text{-th target (Term 1)}} \\\\ \& \\quad + \\underbrace{ \\mathbf{a}_{\\text{Rx}}\^{\\text{H}}(\\hat{\\theta}_{i',\\text{Rx}}) \\left\[ \\sum_{i=1, i\\neq i'}\^{I} \\left\[ \\kappa_{i,S}\^b e\^{j2\\pi(f_{i,S}\^b m T\^b - n \\Delta f\^b \\tau_{i,0})} \\mathbf{a}_{\\text{Rx}}(\\theta_{i,\\text{Rx}})\\mathbf{a}_{\\text{Tx}}\^{\\text{T}}(\\theta_{i,\\text{Tx}})\\mathbf{I} \\right\] \\mathbf{W}_{\\text{Tx}}\^b + \\mathbf{Z}_{m,n}\^{S,b} \\right\] (\\mathbf{W}_{\\text{Tx}}\^b)\^H \\mathbf{a}_{\\text{Tx}}\^\*(\\hat{\\theta}_{i',\\text{Tx}})/(N_R N_T) }_{\\text{Interference (Term 2)}} \\end{aligned} \\tag{19} H\^m,nb,i′=aRxH(θ\^i′,Rx)H\^m,nb(WTxb)HaTx∗(θ\^i′,Tx)/(NRNT)≈The i′-th target (Term 1) κi′,Sbej2π(fi′,SbmTb−nΔfbτi′,0)+Interference (Term 2) aRxH(θ\^i′,Rx) i=1,i=i′∑I\[κi,Sbej2π(fi,SbmTb−nΔfbτi,0)aRx(θi,Rx)aTxT(θi,Tx)I\]WTxb+Zm,nS,b (WTxb)HaTx∗(θ\^i′,Tx)/(NRNT)(19) 根据 (19)，在第 b b b 个 CC 中，在 M b M_b Mb 个 OFDM 符号时间内， N b N_b Nb 个子载波上第 i ′ i' i′ 个目标的回波信号被重写为矩阵形式 D i ′ S , b = S i ′ S , b + Z i ′ S , b (20) \\mathbf{D}_{i'}\^{S,b} = \\mathbf{S}_{i'}\^{S,b} + \\mathbf{Z}_{i'}\^{S,b} \\tag{20} Di′S,b=Si′S,b+Zi′S,b(20) 其中 Z i ′ S , b \\mathbf{Z}_{i'}\^{S,b} Zi′S,b 是一个包含来自其他目标的干扰和噪声的干扰矩阵，而 S i ′ S , b ∈ C N b × M b \\mathbf{S}_{i'}\^{S,b} \\in \\mathbb{C}\^{N_b \\times M_b} Si′S,b∈CNb×Mb 表示一个延迟-多普勒信息矩阵，如后页底部 (21) 所示。 *** ** * ** *** 3. **CCC 方法** ：对于第 i ′ i' i′ 个目标，观察 (21) 可知， S i ′ S , b \\mathbf{S}_{i'}\^{S,b} Si′S,b 在高低频段上的初始相位未对齐，并存在一个不同的复数 κ i ′ , S b \\kappa_{i',S}\^b κi′,Sb。为此，我们执行 CCC 方法 \[18\] 来消除该复数 κ i ′ , S b \\kappa_{i',S}\^b κi′,Sb。将 CCC 方法应用于 D i ′ S , b \\mathbf{D}_{i'}\^{S,b} Di′S,b 的过程在以下步骤中呈现。 * **步骤 1** ：将 D i ′ S , b \\mathbf{D}_{i'}\^{S,b} Di′S,b 分为 N b N_b Nb 个行向量，表示为 D i ′ S , b = \[ ( d i ′ , 0 S , b ) T , ( d i ′ , 1 S , b ) T , ⋯   , ( d i ′ , N b − 1 S , b ) T \] T (22) \\mathbf{D}_{i'}\^{S,b} = \\left\[ \\left(\\mathbf{d}_{i',0}\^{S,b}\\right)\^{\\text{T}}, \\left(\\mathbf{d}_{i',1}\^{S,b}\\right)\^{\\text{T}}, \\cdots, \\left(\\mathbf{d}_{i',N_b-1}\^{S,b}\\right)\^{\\text{T}} \\right\]\^{\\text{T}} \\tag{22} Di′S,b=\[(di′,0S,b)T,(di′,1S,b)T,⋯,(di′,Nb−1S,b)T\]T(22) 其中 d i ′ , n S , b ∈ C 1 × M b \\mathbf{d}_{i',n}\^{S,b} \\in \\mathbb{C}\^{1 \\times M_b} di′,nS,b∈C1×Mb 表示 D i ′ S , b \\mathbf{D}_{i'}\^{S,b} Di′S,b 的第 n n n 个行向量。 * **步骤 2** ：通过累加行向量之间的共轭乘法结果获得一个延迟特征向量 r i ′ b , S ∈ C N b × 1 \\mathbf{r}_{i'}\^{b,S} \\in \\mathbb{C}\^{N_b \\times 1} ri′b,S∈CNb×1，如后页底部的 (23) 所示，其中 z i b \\mathbf{z}_i\^b zib 是一个干扰向量。为保证 r i ′ b , S \\mathbf{r}_{i'}\^{b,S} ri′b,S 的信噪比均匀分布，需要进行加权平均以获得最终的特征向量 g i ′ b , S = r i ′ b , S ⊙ w r \\mathbf{g}_{i'}\^{b,S} = \\mathbf{r}_{i'}\^{b,S} \\odot \\mathbf{w}_r gi′b,S=ri′b,S⊙wr，其中 w r = \[ N b ( N b + 1 ) / 2 , N b − 1 ( N b + 1 ) / 2 , ⋯   , 1 ( N b + 1 ) / 2 \] T \\mathbf{w}_r = \[\\frac{N_b}{(N_b+1)/2}, \\frac{N_b-1}{(N_b+1)/2}, \\cdots, \\frac{1}{(N_b+1)/2}\]\^{\\text{T}} wr=\[(Nb+1)/2Nb,(Nb+1)/2Nb−1,⋯,(Nb+1)/21\]T 是权重向量。 r i ′ , S b = 1 M b \[ 1 N b ∑ a = 0 N b − 1 d i ′ , a S , b ( d i ′ , a S , b ) H , 1 N b − 1 ∑ a = 0 N b − 1 − 1 d i ′ , a + 1 S , b ( d i ′ , a S , b ) H , ⋯   , 1 N b − n ∑ a = 0 N b − n − 1 d i ′ , a + n S , b ( d i ′ , a S , b ) H , ⋯   , d i ′ , N b − 1 S , b ( d i ′ , 0 S , b ) H \] T = \[ 1 , e − j 2 π Δ f b τ i ′ , 0 , ⋯   , e − j 2 π ( N b − 1 ) Δ f b τ i ′ , 0 \] T + z i ′ b . (23) \\begin{aligned} \\mathbf{r}_{i',S}\^b \& = \\frac{1}{M_b} \\left\[ \\frac{1}{N_b} \\sum_{a=0}\^{N_b-1} \\mathbf{d}_{i',a}\^{S,b} (\\mathbf{d}_{i',a}\^{S,b})\^{\\text{H}}, \\frac{1}{N_b-1} \\sum_{a=0}\^{N_b-1-1} \\mathbf{d}_{i',a+1}\^{S,b} (\\mathbf{d}_{i',a}\^{S,b})\^{\\text{H}}, \\cdots, \\frac{1}{N_b-n} \\sum_{a=0}\^{N_b-n-1} \\mathbf{d}_{i',a+n}\^{S,b} (\\mathbf{d}_{i',a}\^{S,b})\^{\\text{H}}, \\cdots, \\mathbf{d}_{i',N_b-1}\^{S,b} (\\mathbf{d}_{i',0}\^{S,b})\^{\\text{H}} \\right\]\^{\\text{T}} \\\\ \& = \\left\[ 1, e\^{-j2\\pi \\Delta f\^b \\tau_{i',0}}, \\cdots, e\^{-j2\\pi(N_b-1)\\Delta f\^b \\tau_{i',0}} \\right\]\^{\\text{T}} + \\mathbf{z}_{i'}\^b. \\end{aligned} \\tag{23} ri′,Sb=Mb1\[Nb1a=0∑Nb−1di′,aS,b(di′,aS,b)H,Nb−11a=0∑Nb−1−1di′,a+1S,b(di′,aS,b)H,⋯,Nb−n1a=0∑Nb−n−1di′,a+nS,b(di′,aS,b)H,⋯,di′,Nb−1S,b(di′,0S,b)H\]T=\[1,e−j2πΔfbτi′,0,⋯,e−j2π(Nb−1)Δfbτi′,0\]T+zi′b.(23) * **步骤 3** ：将 D i ′ S , b \\mathbf{D}_{i'}\^{S,b} Di′S,b 分为 M b M_b Mb 个列向量，表示为 D i ′ S , b = \[ c i ′ , 0 S , b , c i ′ , 1 S , b , ⋯   , c i ′ , M b − 1 S , b \] (24) \\mathbf{D}_{i'}\^{S,b} = \\left\[ \\mathbf{c}_{i',0}\^{S,b}, \\mathbf{c}_{i',1}\^{S,b}, \\cdots, \\mathbf{c}_{i',M_b-1}\^{S,b} \\right\] \\tag{24} Di′S,b=\[ci′,0S,b,ci′,1S,b,⋯,ci′,Mb−1S,b\](24) 其中 c i ′ , m S , b ∈ C N b × 1 \\mathbf{c}_{i',m}\^{S,b} \\in \\mathbb{C}\^{N_b \\times 1} ci′,mS,b∈CNb×1 表示 D i ′ S , b \\mathbf{D}_{i'}\^{S,b} Di′S,b 的第 m m m 个列向量。 * **步骤 4** ：通过累加列向量之间的共轭乘法结果获得一个多普勒特征向量 v i ′ b , S ∈ C 1 × M b \\mathbf{v}_{i'}\^{b,S} \\in \\mathbb{C}\^{1 \\times M_b} vi′b,S∈C1×Mb，如后页底部的 (25) 所示。与延迟特征向量类似，最终的多普勒向量为 e i ′ b , S = v i ′ b , S ⊙ w v \\mathbf{e}_{i'}\^{b,S} = \\mathbf{v}_{i'}\^{b,S} \\odot \\mathbf{w}_v ei′b,S=vi′b,S⊙wv，其中 w v = \[ M b ( M b + 1 ) / 2 , M b − 1 ( M b + 1 ) / 2 , ⋯   , 1 ( M b + 1 ) / 2 \] \\mathbf{w}_v = \[\\frac{M_b}{(M_b+1)/2}, \\frac{M_b-1}{(M_b+1)/2}, \\cdots, \\frac{1}{(M_b+1)/2}\] wv=\[(Mb+1)/2Mb,(Mb+1)/2Mb−1,⋯,(Mb+1)/21\] 是权重向量。完成以上步骤后，即可获得 I I I 个目标的特征向量集，即 { g i ′ 1 , S } i ′ = 1 , 2 , ⋯   , I \\{\\mathbf{g}_{i'}\^{1,S}\\}_{i'=1,2,\\cdots,I} {gi′1,S}i′=1,2,⋯,I、 { e i ′ 1 , S } i ′ = 1 , 2 , ⋯   , I \\{\\mathbf{e}_{i'}\^{1,S}\\}_{i'=1,2,\\cdots,I} {ei′1,S}i′=1,2,⋯,I、 { g i ′ 2 , S } i ′ = 1 , 2 , ⋯   , I \\{\\mathbf{g}_{i'}\^{2,S}\\}_{i'=1,2,\\cdots,I} {gi′2,S}i′=1,2,⋯,I 和 { e i ′ 2 , S } i ′ = 1 , 2 , ⋯   , I \\{\\mathbf{e}_{i'}\^{2,S}\\}_{i'=1,2,\\cdots,I} {ei′2,S}i′=1,2,⋯,I。 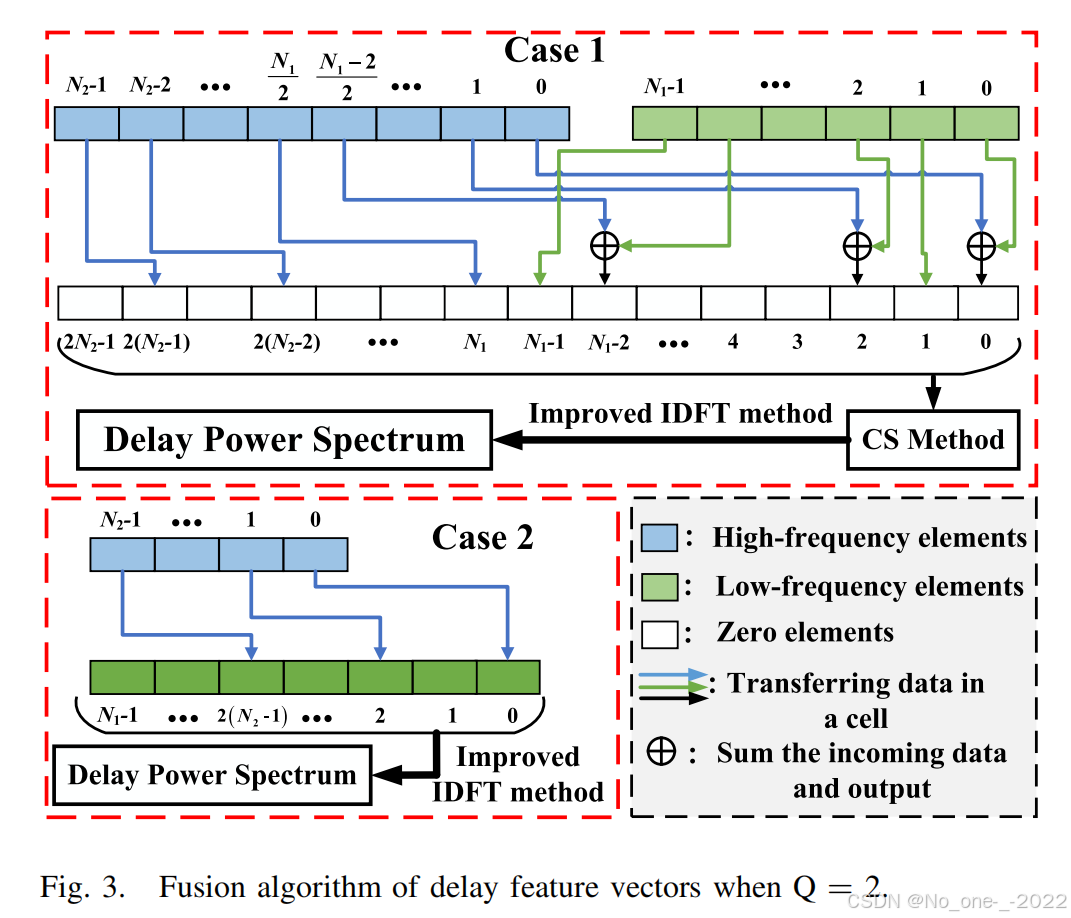 #### B. Sensing Performance Analysis 1. **MIMO-OFDM 系统的 CRLB** ：OFDM ISAC 系统的 CRLB 已在 \[8\] 中推导得出，而 MIMO-OFDM ISAC 系统的 CRLB 则在**定理 3** 中给出。为便于推导，使用 γ i = 2 v i , 0 c \\gamma_i = \\frac{2v_{i,0}}{c} γi=c2vi,0 作为速度的估计值，以避免变化的载波频率对理论推导的影响 \[8\]。同时，使用 sin ⁡ θ i , Rx \\sin\\theta_{i,\\text{Rx}} sinθi,Rx 作为 AoA 的估计值，以避免多次推导后出现未知参数 \[44\], \[45\], \[46\]。 > **定理 3** ：对于一个 MIMO-OFDM ISAC 系统（例如第 b b b 个 CC）， sin ⁡ θ i , Rx \\sin\\theta_{i,\\text{Rx}} sinθi,Rx、 τ i , 0 \\tau_{i,0} τi,0 和 γ i \\gamma_i γi 的克拉美-罗下限 (CRLB) 分别由 (47)、(48) 和 (49) 表示。 > CRLB ( sin ⁡ θ i , Rx ) = Γ mimo N R \[ M b N b Θ b m − ( Θ b m , n ) 2 \] M b N b 2 (47) \\text{CRLB}(\\sin\\theta_{i,\\text{Rx}}) = \\frac{\\Gamma_{\\text{mimo}} N_R \\left\[ M_b N_b \\Theta_b\^m - (\\Theta_b\^{m,n})\^2 \\right\]}{M_b N_b\^2} \\tag{47} CRLB(sinθi,Rx)=MbNb2ΓmimoNR\[MbNbΘbm−(Θbm,n)2\](47) CRLB ( τ i , 0 ) = Γ mimo N b \[ M b N R Θ b p − ( Θ b p , m ) 2 \] M b N R (48) \\text{CRLB}(\\tau_{i,0}) = \\frac{\\Gamma_{\\text{mimo}} N_b \\left\[ M_b N_R \\Theta_b\^p - (\\Theta_b\^{p,m})\^2 \\right\]}{M_b N_R} \\tag{48} CRLB(τi,0)=MbNRΓmimoNb\[MbNRΘbp−(Θbp,m)2\](48) CRLB ( γ i ) = Γ mimo M b \[ N b N R Θ b n − ( Θ b p , n ) 2 \] N b N R (49) \\text{CRLB}(\\gamma_i) = \\frac{\\Gamma_{\\text{mimo}} M_b \\left\[ N_b N_R \\Theta_b\^n - (\\Theta_b\^{p,n})\^2 \\right\]}{N_b N_R} \\tag{49} CRLB(γi)=NbNRΓmimoMb\[NbNRΘbn−(Θbp,n)2\](49) > > 其中 Γ mimo \\Gamma_{\\text{mimo}} Γmimo 由后页底部的 (50) 表示， ϖ = ∣ A ∣ 2 σ z 2 \\varpi = \\frac{\|A\|\^2}{\\sigma_z\^2} ϖ=σz2∣A∣2， Θ b n = ∑ ( n Δ f b ) 2 \\Theta_b\^n = \\sum(n\\Delta f\^b)\^2 Θbn=∑(nΔfb)2， Θ b m = ∑ ( m f c b T b ) 2 \\Theta_b\^m = \\sum(mf_c\^b T\^b)\^2 Θbm=∑(mfcbTb)2， Θ b p = ∑ p ( p d r λ b ) 2 \\Theta_b\^p = \\sum_p(p\\frac{d_r}{\\lambda\^b})\^2 Θbp=∑p(pλbdr)2， Θ b m , n = ∑ m ∑ n m n Δ f b f c b T b \\Theta_b\^{m,n} = \\sum_m\\sum_n mn\\Delta f\^b f_c\^b T\^b Θbm,n=∑m∑nmnΔfbfcbTb， Θ b p , n = ∑ p ∑ n p n d r λ b Δ f b \\Theta_b\^{p,n} = \\sum_p\\sum_n pn\\frac{d_r}{\\lambda\^b}\\Delta f\^b Θbp,n=∑p∑npnλbdrΔfb，且 Θ b p , m = ∑ p ∑ m p m d r λ b f c b T b \\Theta_b\^{p,m} = \\sum_p\\sum_m pm\\frac{d_r}{\\lambda\^b} f_c\^b T\^b Θbp,m=∑p∑mpmλbdrfcbTb。