计算机算术8-浮点加法

#1. 基本方案

浮点加减法采用小阶向大阶看齐，先进行对齐，然后运算，最后归一化的操作，具体入下图所示

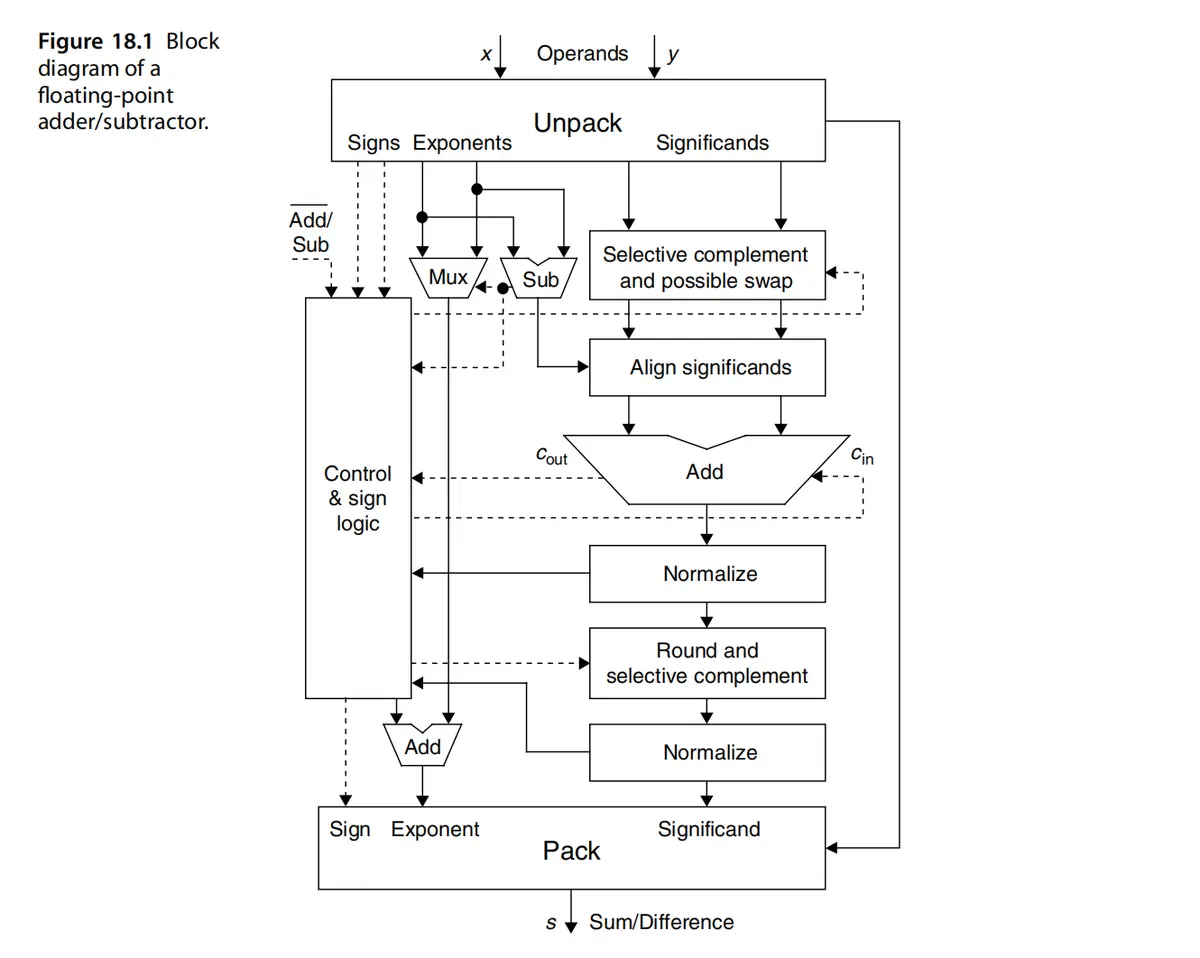
1. 符号位: 选择较大数的符号位
2. 指数位: 选择较大数的指数位，然后根据最终value的归一化操作时，对指数进行运算
3. 尾数位: 先小阶向大阶看齐(移位)，进行运算，最后归一化，然后进行舍入运算，最后进一步归一化。输出最终结果

2. 方案优化

2.1 pre-shifting & post-shifting

1. 小阶向大阶看齐的移位，本质是尾数的右移，那么尾数位宽最多只有23bit(sp), 因此移位量只用5bit就可以表示， 指数的差值不用全部计算出来。其中32to1的mux，fan-in和fan-out太大，我们可以用multi-stage的mux
   
   
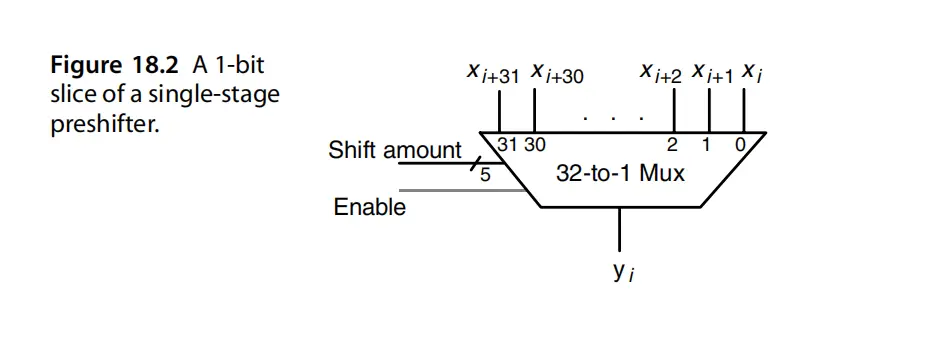
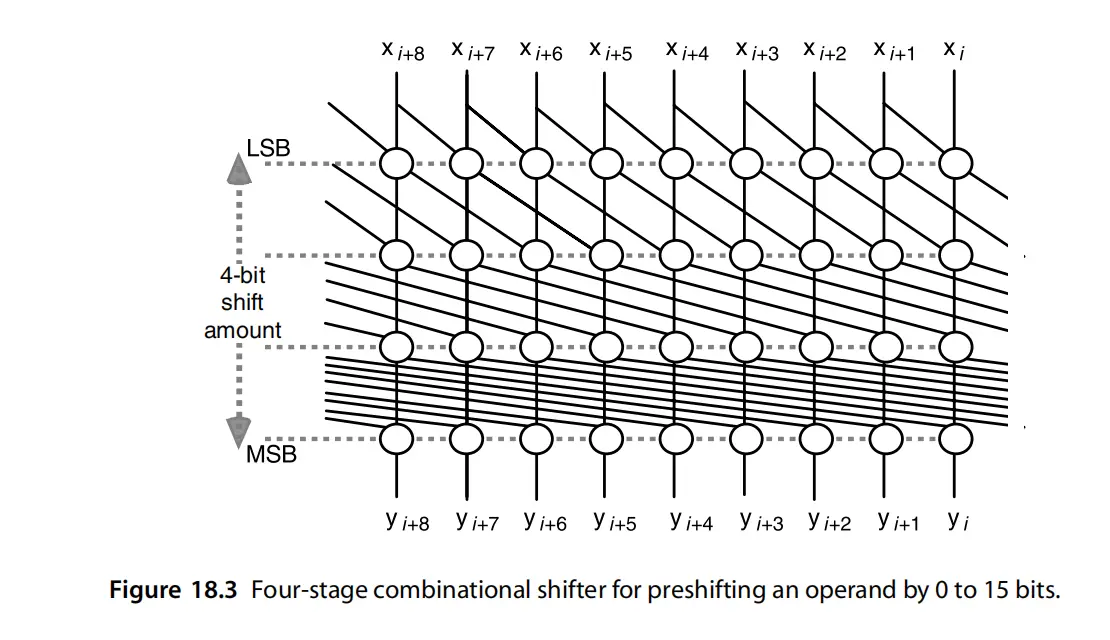
2. 为了避免e1-e2出现负数的情况，我们通常既计算e1-e2, 也计算e2-e1 来并行处理
3. post-shifting主要有右移1bit, 和左移0-31bit的情况，其中右移1bit表示舍入之后指数需要加1。左移0-31bit, 表示运算之后出现了很多前导0，需要进行左移归一化处理，然后指数减去对应的前导零个数
4. 左移有两种方式，一种是根据计算结果的值，然后我们统计前导0的个数，最后进行移位，是一个串行过程。我们可以根据前导零预测算法，不需要根据计算结果进行统计，这样前导零的计算和结果的计算就可以并行处理了。
   
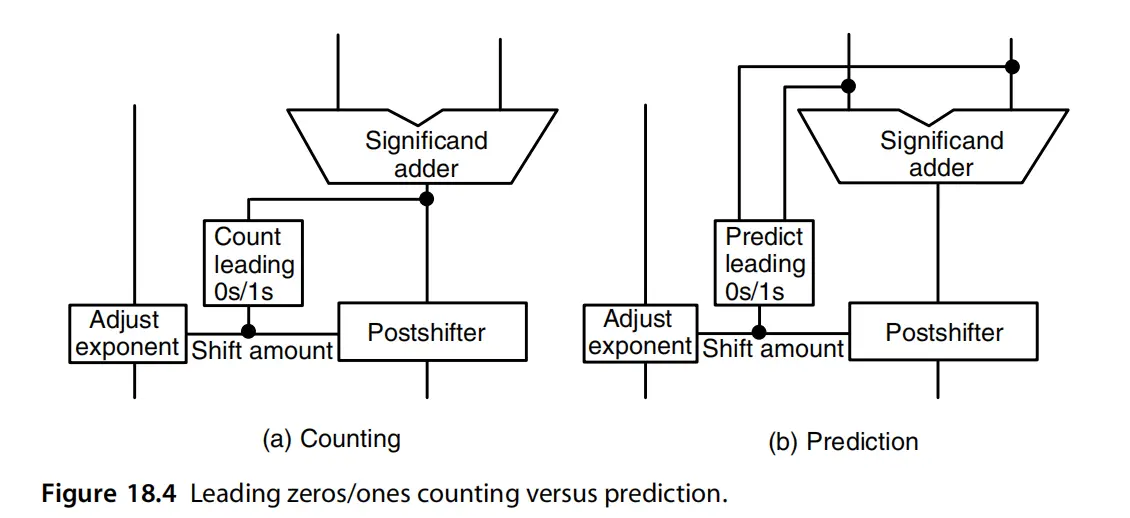
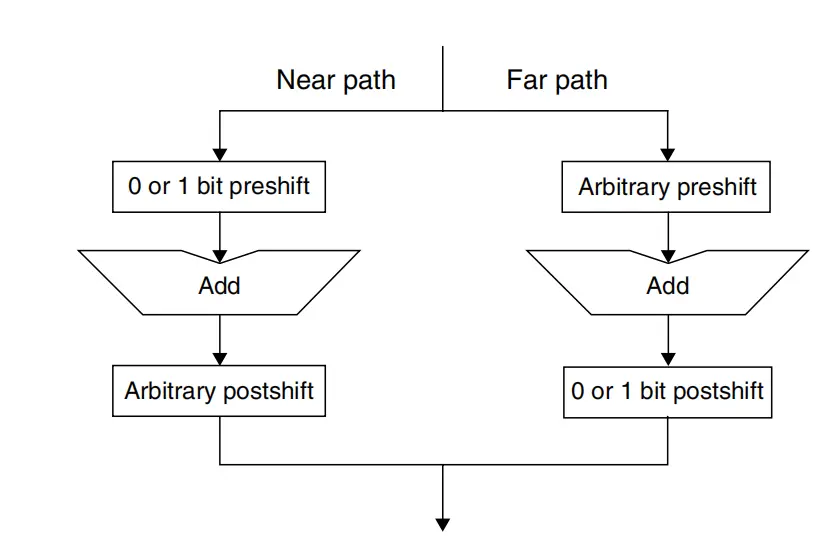
5. near-path & far-path, near-path表示两者的指数相差不超过1，并且是减法，这样我们的pre-shift最多只会移动移位，其他的fa-path的post-shitf也最多只会右移一位。