代码随想录算法训练营第四十三天 | 图论理论基础、深搜理论基础、卡码网98. 所有可达路径、797. 所有可能的路径、广搜理论基础

代码随想录算法训练营第四十三天任务

图论理论基础
深搜理论基础
[卡码网98. 所有可达路径](#卡码网98. 所有可达路径)
[797. 所有可能的路径](#797. 所有可能的路径)
广搜理论基础

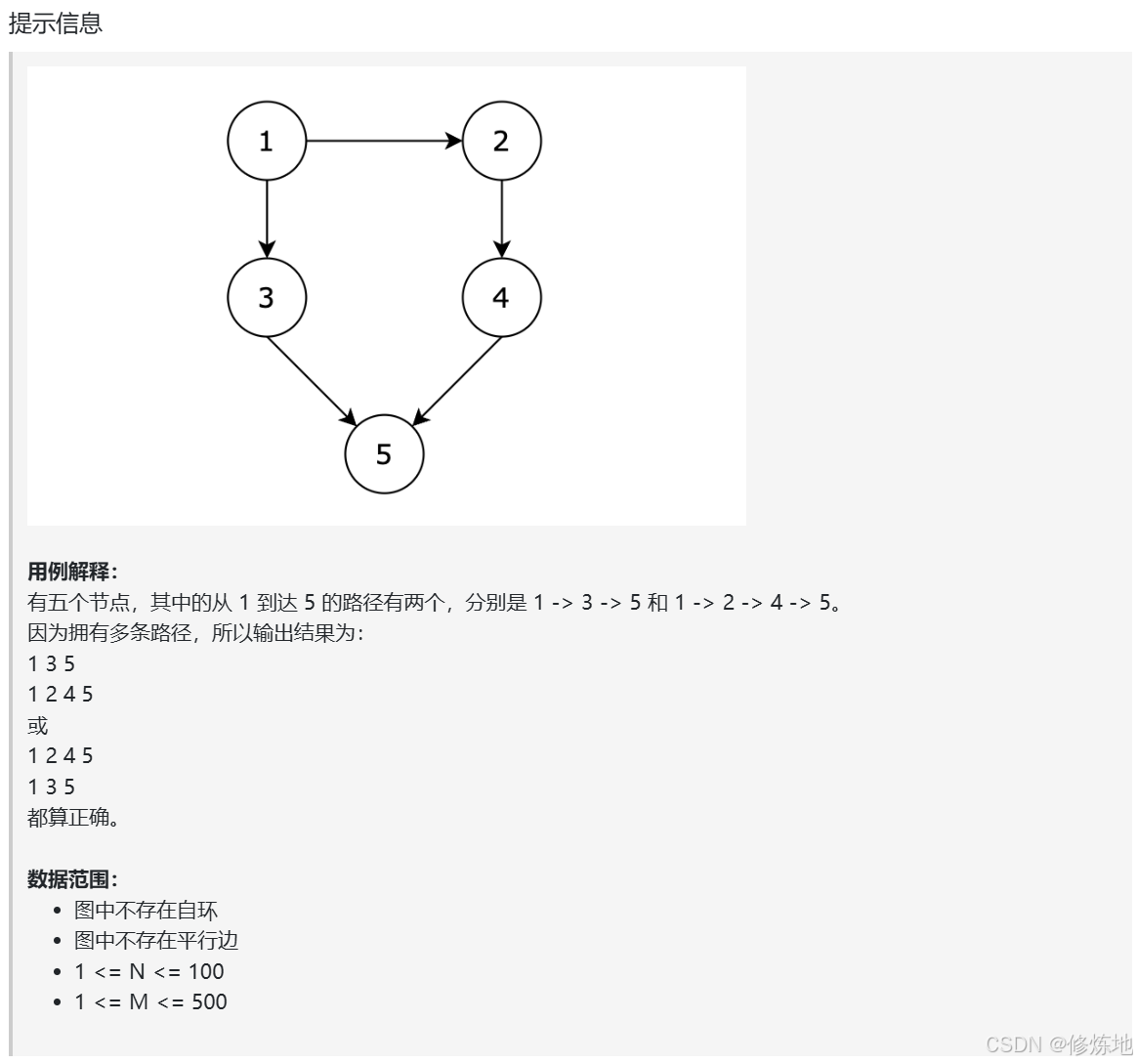
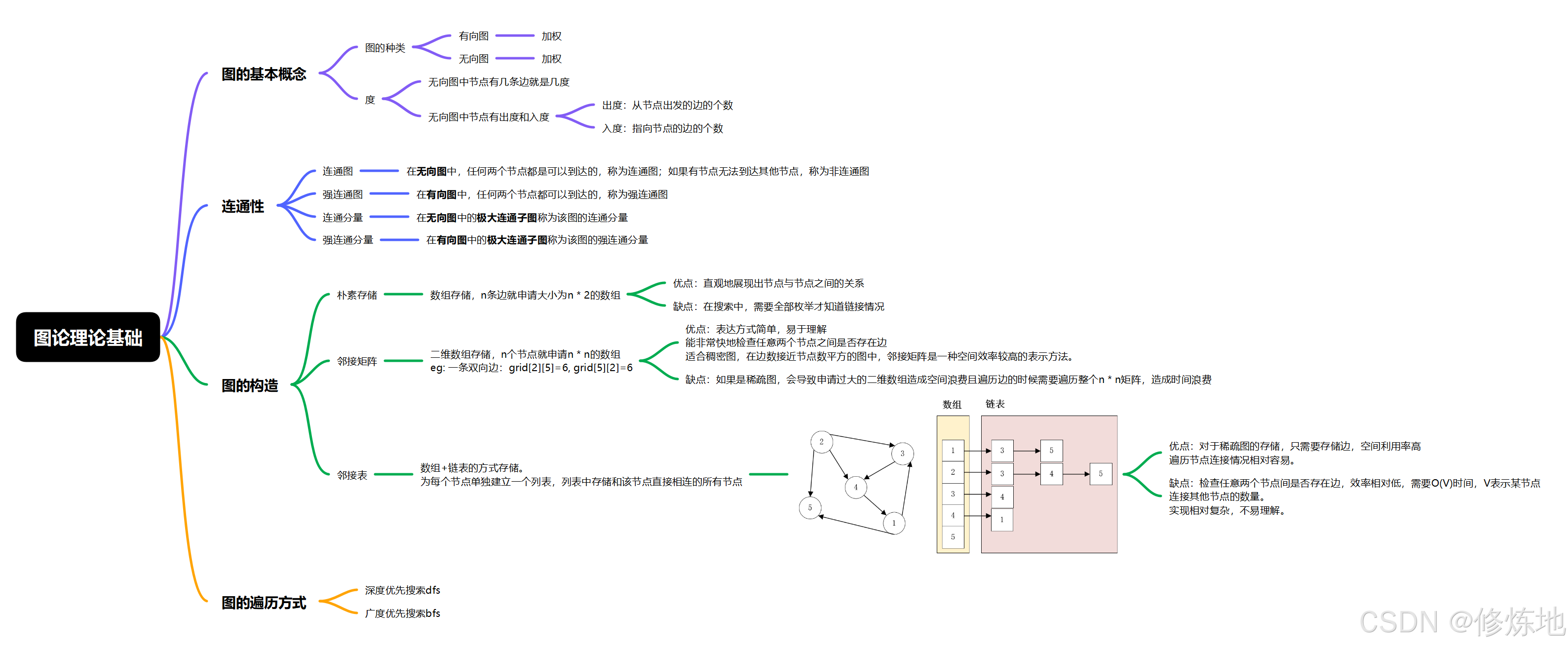
图论理论基础

深搜理论基础

深度优先搜索dfs本质是递归+回溯，往一个方向搜索，搜到底，再回撤换方向搜索。

代码框架和回溯法的代码框架类似。

cpp 复制代码

vector<vector<int>> result; // 保存符合条件的所有路径
vector<int> path; // 起点到终点的路径
void dfs(图，目前搜索节点) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本节点所连接的其他节点) {
        处理节点;
        dfs(图，选择的节点); // 递归
        回溯，撤销处理结果
    }
}

卡码网98. 所有可达路径

题目连接：卡码网98. 所有可达路径

图的表示方法：邻接矩阵和邻接表

cpp 复制代码

//邻接矩阵
vector<vector<int>> graph(n+1, vector<int>(n+1, 0))
graph[s][t] = 1;   // 1表示节点s指向节点t

// 邻接表
vector<list<int>> graph(n+1);
graph[s].push_back(t);   // 表示 s -> t 是相连的

cpp 复制代码

#include <iostream>
#include <vector>
using namespace std;

vector<int> path;
vector<vector<int>> result;
void dfs(const vector<vector<int>>&graph, int x, int n) {
    if (x == n) {
        result.push_back(path);
        return;
    }
    for (int i = 1; i <= n; ++i) {
        if (graph[x][i] == 1) {
            path.push_back(i);
            dfs(graph, i, n);
            path.pop_back();
        }
    }
}
int main() {
    int n, m;
    cin >> n >> m;
    vector<vector<int>> graph(n + 1, vector<int>(n+1, 0));
    while(m--) {
        int s,t;
        cin >> s >> t;
        graph[s][t] = 1;
    }

    path.push_back(1);  // 如何路径都是从节点1开始
    dfs(graph, 1, n);

    if (result.size() == 0) cout << -1 << endl;   // 不存在任何一条路径，输出 -1 
    for (int i = 0; i < result.size(); ++i) {
        for(int j = 0; j < result[i].size()-1; ++j) {
            cout << result[i][j] << " ";
        }
        cout << result[i][result[i].size()-1] << endl;
    }

    return 0;
}

邻接表深搜写法：

cpp 复制代码

void dfs (const vector<list<int>>& graph, int x, int n) {

    if (x == n) { // 找到符合条件的一条路径
        result.push_back(path);
        return;
    }
    for (int i : graph[x]) { // 找到 x指向的节点
        path.push_back(i); // 遍历到的节点加入到路径中来
        dfs(graph, i, n); // 进入下一层递归
        path.pop_back(); // 回溯，撤销本节点
    }
}

797. 所有可能的路径

题目链接：797. 所有可能的路径

有了上题的铺垫，这道题就简单了，按照深搜模板就可写出来。

cpp 复制代码

class Solution {
private:
    vector<int> path;
    vector<vector<int>> result;
    void dfs(const vector<vector<int>>& graph, int x, int n) {
        if (x == n-1) {       // 搜索到n-1，保存路径
            result.push_back(path);
            return;
        }
        for (int i = 0; i < graph[x].size(); ++i) {
            path.push_back(graph[x][i]);
            dfs(graph, graph[x][i], n);
            path.pop_back();  // 回溯
        }
    }
public:
    vector<vector<int>> allPathsSourceTarget(vector<vector<int>>& graph) {
        path.push_back(0);  // 每条路径从0开始。
        int n = graph.size(); 
        dfs(graph, 0, n);
        return result;  
    }
};

时间复杂度：

最坏情况，假设图是完全有向无环图（每个节点 i 都能指向所有编号大于 i 的节点），此时从0到n-1的路径数量是2^n-2(节点1到节点n-2每个都有"选"或"不选"两种可能)，每条路径的长度是n(比如0→1→2→...→n-1)

总操作数 = 路径数 × 单条路径长度 ≈ 2^n-2 × n

因此时间复杂度为O(n × 2ⁿ）忽略常数系数2^-2。

空间复杂度：递归栈深度O(N)。

广搜理论基础

广度优先搜索bfs是一圈一圈的搜索。

广搜的过程就是给出一个start起始位置，从上下左右四个方向走出第一步。

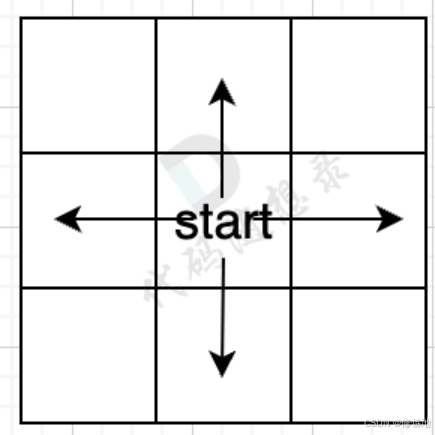
广搜代码框架：

cpp 复制代码

int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 表示四个方向
// grid 是地图，也就是一个二维数组
// visited标记访问过的节点，不要重复访问
// x,y 表示开始搜索节点的下标
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que; // 定义队列
    que.push({x, y}); // 起始节点加入队列
    visited[x][y] = true; // 只要加入队列，立刻标记为访问过的节点
    while(!que.empty()) { // 开始遍历队列里的元素
        pair<int ,int> cur = que.front(); que.pop(); // 从队列取元素
        int curx = cur.first;
        int cury = cur.second; // 当前节点坐标
        for (int i = 0; i < 4; i++) { // 开始想当前节点的四个方向左右上下去遍历
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1]; // 获取周边四个方向的坐标
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 坐标越界了，直接跳过
            if (!visited[nextx][nexty]) { // 如果节点没被访问过
                que.push({nextx, nexty});  // 队列添加该节点为下一轮要遍历的节点
                visited[nextx][nexty] = true; // 只要加入队列立刻标记，避免重复访问
            }
        }
    }

}

和二叉树的层序遍历是相似的，这里用一个visited数组来标记访问过的节点。

用一个4*2的数组表示方向，方便获取当前节点四个方向的坐标。