程序员必读：CPU运算原理深度剖析与浮点数精度问题实战指南

• 引言

• CPU如何实现逻辑运算

  • NMOS和PMOS
  • 基于MOS管组合下的逻辑门运算
  • 逻辑运算下运算的实现
  • ALU的诞生
  • CPU的诞生

• 关于二进制运算的研究

  • 十进制转二进制基础换算
  • 为什么负数要使用补码进行表示
  • 为什么反码就能解决正负数相加问题，我们还需要用补码来表示负数呢？
  • 小数的二进制转换

• 计算机如何保存带有小数的数据

  • 科学计数法
  • 如何用二进制空间表示科学计数法的结果

• 详解0.1+0.2==0.3返回false

  • 问题描述
  • 解决方案
  • 编程中运算的一点建议

• 小结

• 参考

引言

本文将从CPU演变的视角逐步说明CPU的演进过程，同时也会针对计算机数学运算过程中一些常见的错误细节进行探讨。

我是 SharkChili ，Java 开发者，Java Guide 开源项目维护者。欢迎关注我的公众号：写代码的SharkChili ，也欢迎您了解我的开源项目 mini-redis：github.com/shark-ctrl/...

为方便与读者交流，现已创建读者群。关注上方公众号获取我的联系方式，添加时备注加群即可加入。

CPU如何实现逻辑运算

NMOS和PMOS

CPU是由晶体管构成的，在逻辑上我们一般会将其通过电路符号进行抽象，即分为如下三个连接端：

1. 栅极(gate)
2. 源极(source)
3. 漏极(drain)

基于NMOS而言，从语义上来理解，它是N型MOS管(N即negative)，所以它的电流控制方式是：当栅极输入高电平(1)时，NMOS导通，电流可以从漏极流向源极；当栅极输入低电平(0)时，NMOS截止，电流无法流通。下图中寄生二极管(即右边的箭头)的朝向是由源极(S)到漏极(D)，这样可以避免漏极电流无条件从漏极流向源极。NMOS的工作机制为：

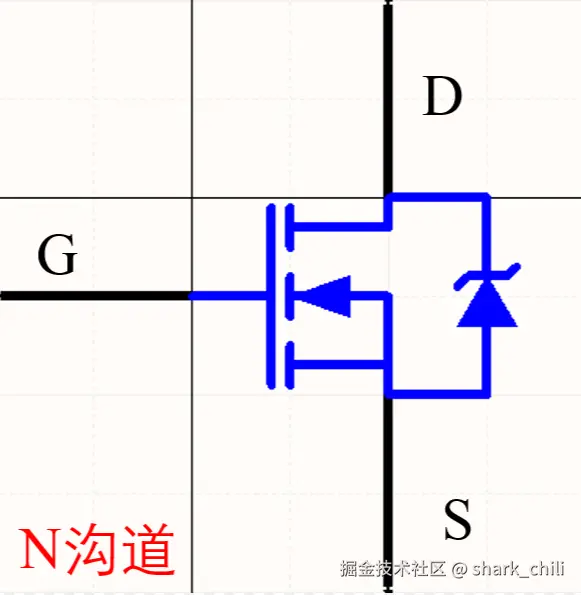
1. 当输入二进制1时，栅极闭合，电路导通，电流从漏极流向源极
2. 当输入二进制0时，栅极电源断开，电路无法导通

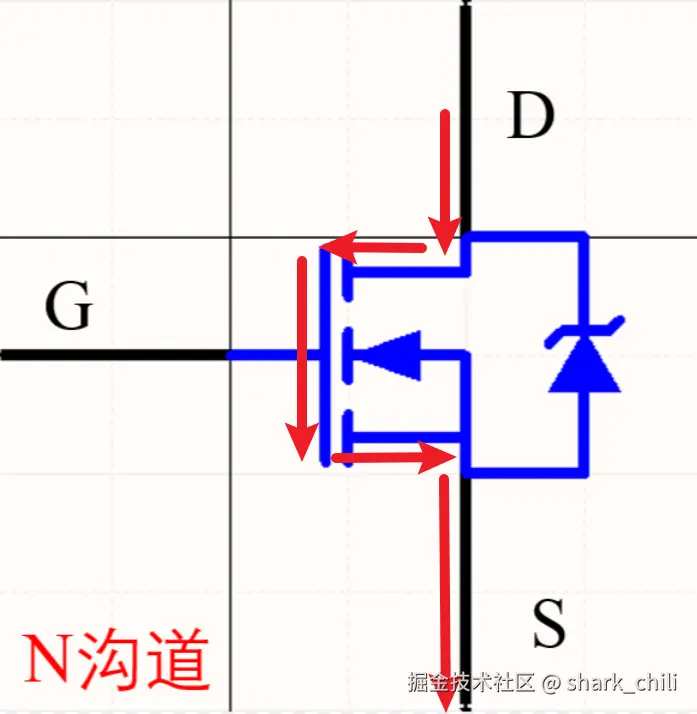
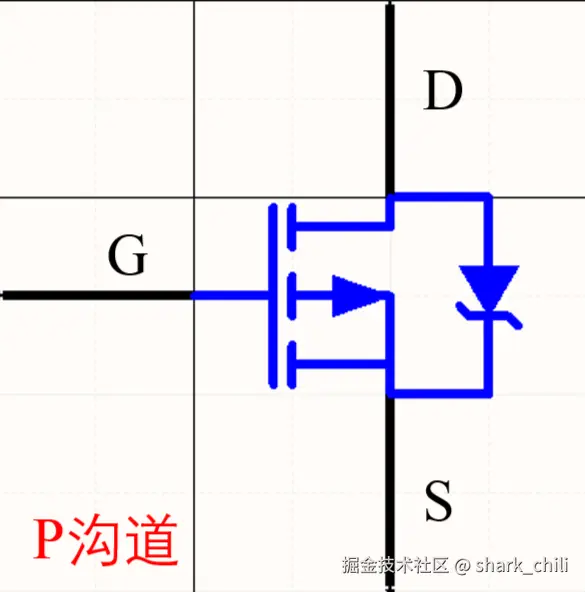
PMOS则相反，可以看到寄生二极管从漏极指向源极避免源极无条件流向漏极，因为PMOS是P型MOS管(P即positive)，其工作机制与NMOS相反：

1. 当输入0时，栅极闭合，电路直接导通，从源极直接流向漏极
2. 当输入1时，栅极断开，电路无法导通

基于MOS管组合下的逻辑门运算

基于上述电路符号的基础上，我们将二者结合，NMOS接地、PMOS接电源，试想这样我们输入数字1：

1. 对于NMOS电源导通，输出端Y导通，接地连同
2. 对于PMOS电源断开，与电源端断开
3. 最终没有亮起输出0

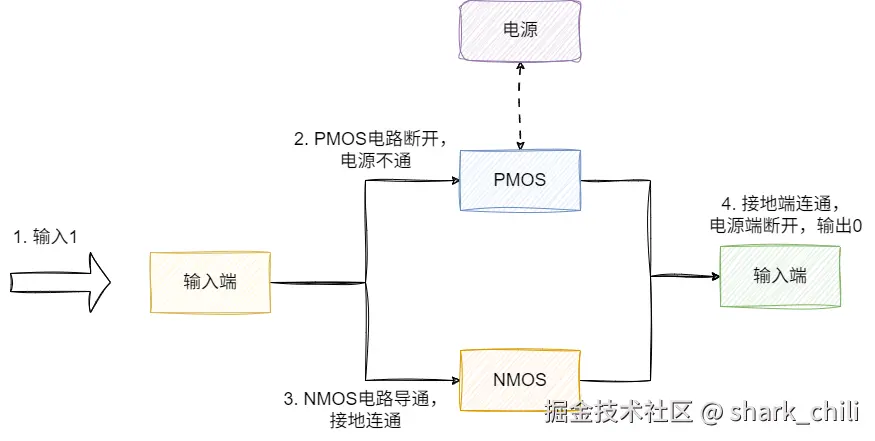
同理，我们不妨再尝试输入0：

1. 对于NMOS电源断开
2. 对于PMOS电源导通
3. 电源端导通，输出1

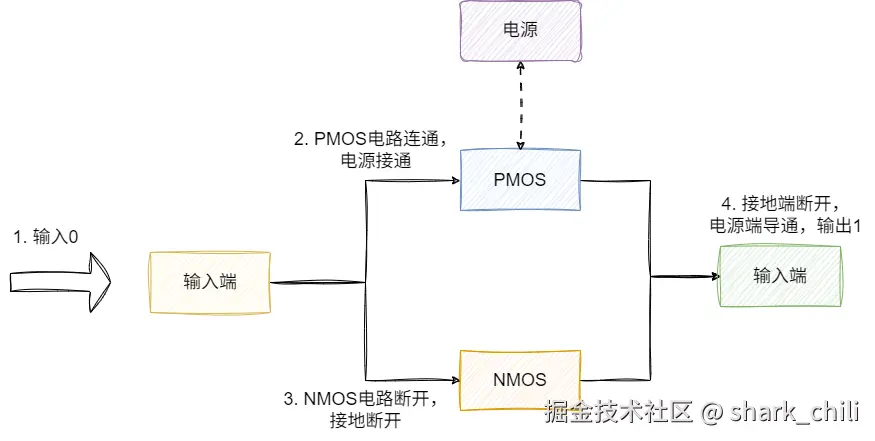
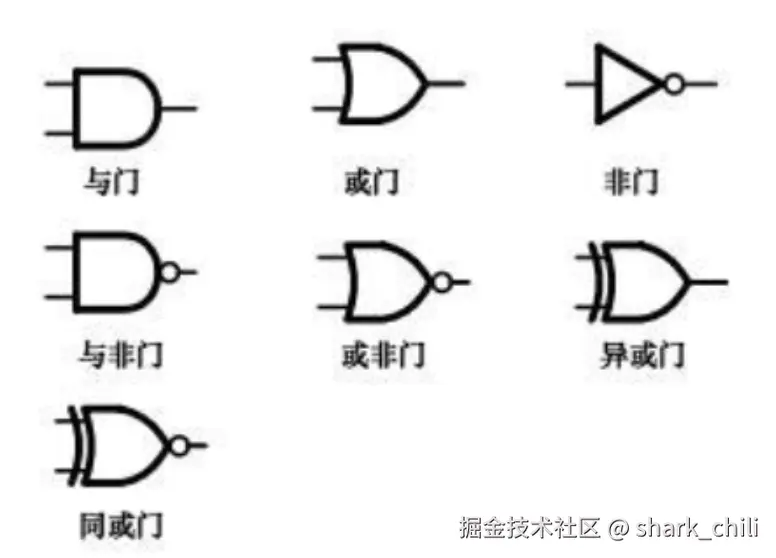
由此可知，输出结果与输入结果相反，就生成二进制中的非运算，而上述的组合我们也称之为非门。同理，设计者们基于NMOS和PMOS这两种晶体管搭建出各种各样的门电路：

1. 与门
2. 或门
3. 非门
4. 与非门
5. 或非门
6. 异或门
7. ......

逻辑运算下运算的实现

基于逻辑门的基础，我们开始推进计算机运算的步骤，我们都知道计算机是二进制语言，对应我们以加法为例，对应的运算为：

1. 0+0=0 即二进制的00+00，最终输出二进制结果为00
2. 0+1=1 即二进制中的00+01，最终输出二进制结果为01
3. 1+1=2 即二进制中的01+01，最终输出二进制结果为10

最终我们将这些数字的二进制运算转换为如下图所示的表格，我们以1+1为例，可以看到输出二进制结果为10，对应的低位为0，而进位为1，由此得出10。

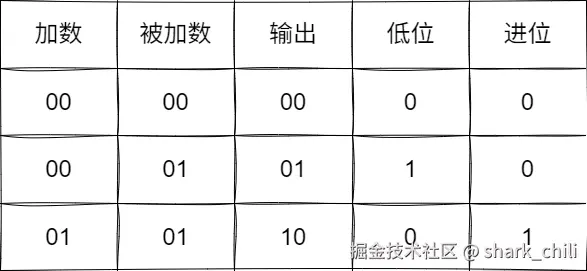
我们从最基础的规律抓起，可以看到低位的值本质上就是异或运算：

1. 第一行低位的0本质上就是 0^0，对应输出0
2. 第二行低位的1本质上就是 0^1，对应输出1
3. 第三行低位的0本质上就是 1^1，对应输出0

然后我们就需要考虑另一个问题，即进位问题，经过推理发现本质上就是按位与，同样结合表格可以看出，对应的进位本质上就是两个输入位的按位与：

1. 第一行进位0本质上就是 0&0，对应输出0
2. 第二行进位0本质上就是 0&1，对应输出0
3. 第三行进位1本质上就是 1&1，对应输出1

最终我们完成低位的加法运算推导过程，即通过：

1. 异或门计算低位和
2. 与门计算进位

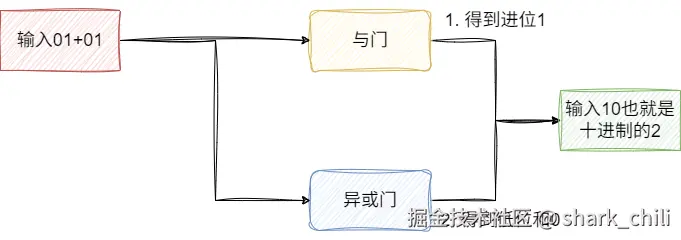
对应的我们将上述的逻辑视图换成如下符号表示，读者可结合图片中的语义自行理解：

但是加法中还是涉及一些高位累加的情况，例如15+9对应9+5的进位就需要参与到高位的运算中，所以说我们目前的加法器只是一个简单的半加法器。

关于二进制进位的运算，需要考虑低位的进位输入，我们试想3+3即二进制的11和11相加，对应的换算步骤为：

1. 低位两个1使用半加器算得和为0、进位1。
2. 高位两个1使用半加器算得和为0、进位1。
3. 因为低位有个进位1，需要与高位的和也就是0相加。
4. 结合低位和0，高位和与低位进位处理得到最终结果，高位进位1，得到二进制110也就是6：

同理我们再演示一下2+2也就是二进制10和10相加：

1. 低位算得和0进位也为0
2. 高位算得和为0进位为1
3. 低位进位0和高位和0处理得到结果
4. 结合低位0、高位和与低位进位0算法低2位为0，高位进位为1即100
5. 最终结果为4

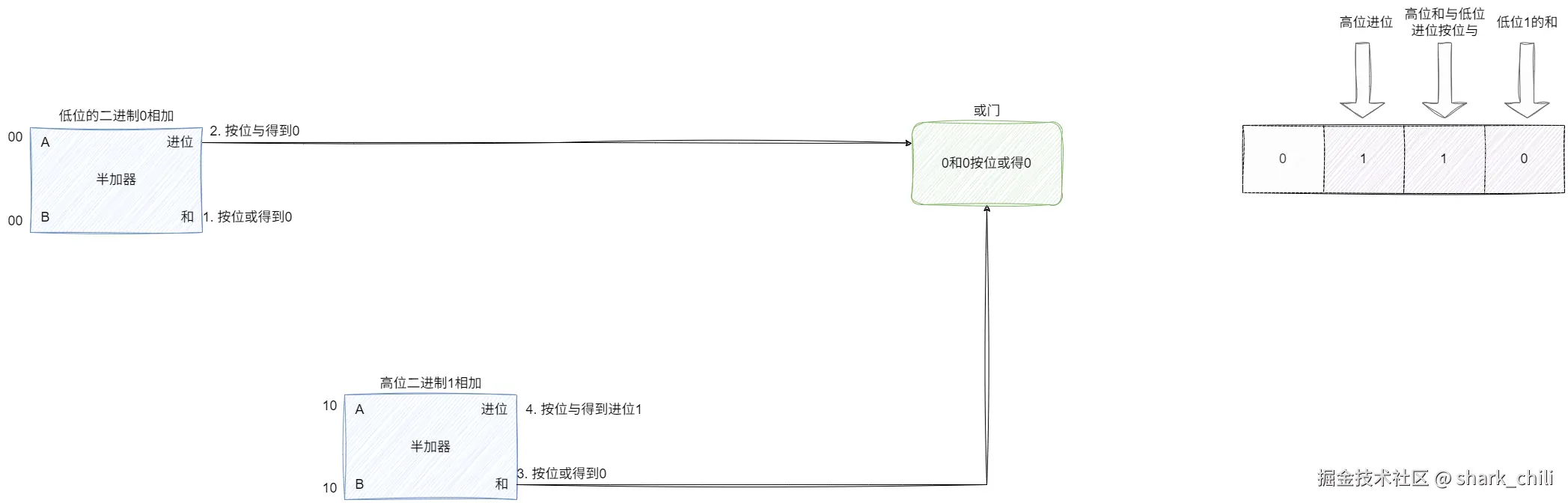
通过这种运算，我们推理出全加法器，在此基础上，串联无数个全加法器生成更高进位的加法运算。

ALU的诞生

有了加法的基础，我们即可实现更多的运算，通过数学基础我们可知：

1. 除法本质就是减法，例如12/3=4，本质上就是：

12-3=9 商为1
9-3=6 商为2
6-3=3 商为3
3-3=0 商为4

2. 减法本质上就是加上负数的加法 3. 乘法本质就是加法

由此我们基于复用的思想利用全加器构成了完整的运算系统：

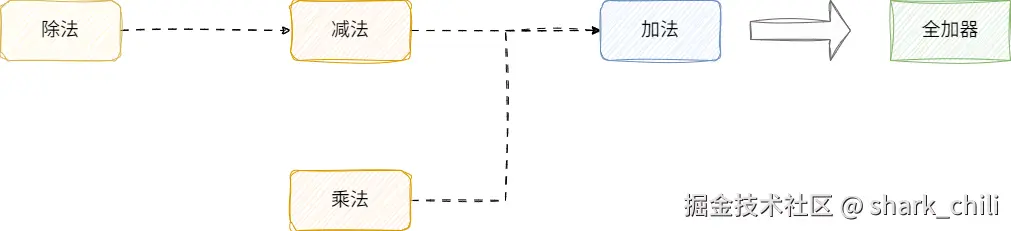
CPU的诞生

基于上述逻辑电门和算数运算进行组合打包就变成了一个全新的部件，即算数逻辑单元(ALU)，基于功能计算需求越来越强，逻辑门电路越来越多，对应的晶体管数量也越来越多，人类也在不断缩小晶体管的体积，最终借由光刻机的技术，实现了纳米级的晶体管，将这些晶体管组合在一起，在微观的世界里就像是一个巨大的城市，承载着计算机所有的逻辑和运算工作，这也就是我们如今所说的CPU.

关于二进制运算的研究

十进制转二进制基础换算

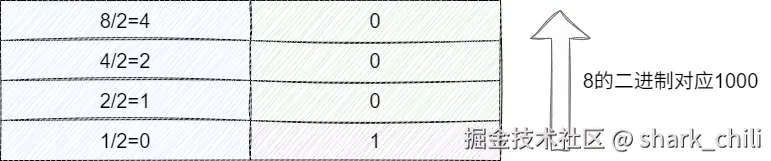
上文提及在计算机中数据都采用二进制表示，对应我们也给出十进制数8的换算过程复习一下二进制的推算过程，如下所示，对应十进制换算二进制的方式本质上就是通过不断整除直到结果为0为止：

为什么负数要使用补码进行表示

该问题我们直接采用反证法来说明，如下图对应-2+1的加法运算，可以看到若负数没有采用补码的形式则计算结果为-3，很明显这种做法是不符合预期的，尽管我们可以在算法上进行优化做到这一点，但势必会增加算法的复杂度：

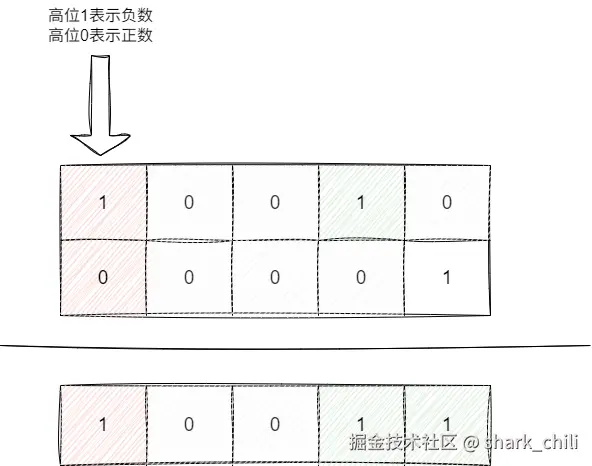
所以我们针对负数的表示进行改良，可以看出正负数是相反的，那么我们有没有一种方法来表示这样的对称关系呢？ 答案是反码，即通过正数的二进制表示形式全部反过来，我们还是以-2+1为例进行一下计算，对应计算步骤如下：

1. 因为-2为负数，所以高位为1，将二进制数0010取反算得1101，然后再+1算得补码1110
2. 对应1的二进制数为0001
3. 相加后算法高位为1的补码数1111
4. 因为之前算补码时+1，此时就需要-1还原，算得1110
5. 将反码还原0001，结合高位为1即负数
6. 最终结果为-1

对应图解步骤如下：

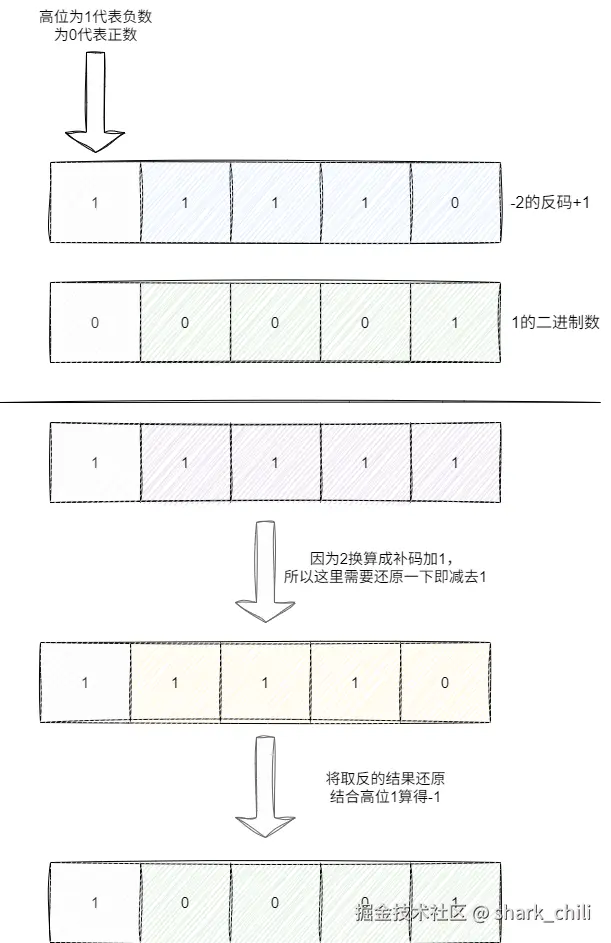
为什么反码就能解决正负数相加问题，我们还需要用补码来表示负数呢？

很简单，我们用反码计算方式算一下3+(-2)

1的二进制为

00000000 00000000 00000000 00000001

-2用反码表示为

11111111 11111111 11111111 11111101

最终结果为全0,很明显计算异常了

00000000 00000000 00000000 00000000

所以为了避免这种计算异常我们就需要对反码+1得到补码，避免反码和正常二进制相加数据溢出导致全0的问题

所以-2使用补码可以表示为

11111111 11111111 11111111 11111110

最终运算结果就是1

小数的二进制转换

上文提及整数的二进制换算就是不断除2直到商为0为止，而小数反之，则是不断乘2直到小数部分为0为止，这里我们就以8.625为例演示一下换算步骤：

1. 整数部分8得到1000
2. 0.625*2经过计算得到1.25取整数位1
3. 接步骤2得到的小数0.25继续乘2，得到0.5，整数位取0
4. 接步骤3得到的小数位继续乘2，得到1.0，取整数位1
5. 对应小数位为0，运算结束

最终结果为1000.101，计算步骤图解如下：

同理，还原步骤也是类似，以上图换算步骤可知解题步骤为：

1. 第一行的1是由0.625*2换算而来的1，所以还原是直接基于这个1除2即可
2. 第二行是0，是由0.62522换算而来的，所以还原时需要除1/4
3. 第三行同理除1/8

最终的换算结果如下：

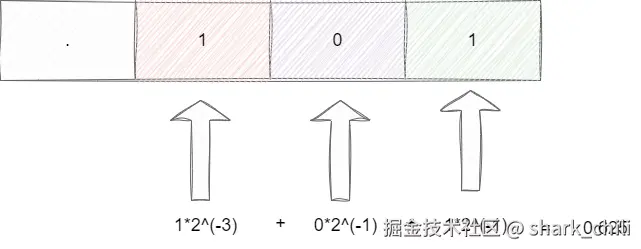
当然，也不是所有的小数都可以得到这样完美的结果，例如0.1的二进制表示，可以看到笔者经过一阵演算过后会走到环路造成无限二进制：

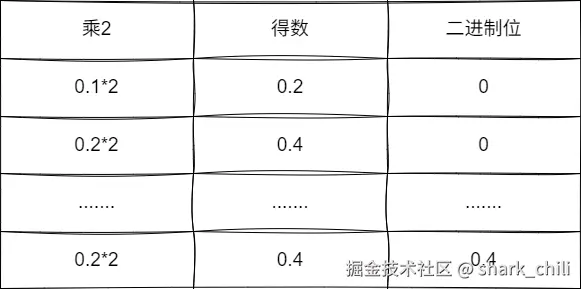
计算机如何保存带有小数的数据

科学计数法

首先我们需要了解一下科学计数法，例如1230000化为1.23*10(^6)这种就是科学计数法，即整数部分只有一个数字，像 12.3 *10(^5)就不是科学计数法了

同理上文，8.625得到的二进制值为1000.101，参照十进制的计算方式我们也可以得出科学计数法结果为1.000101*2(^3)(小数点向左移动三位变小了，所以需要*2(^3))：

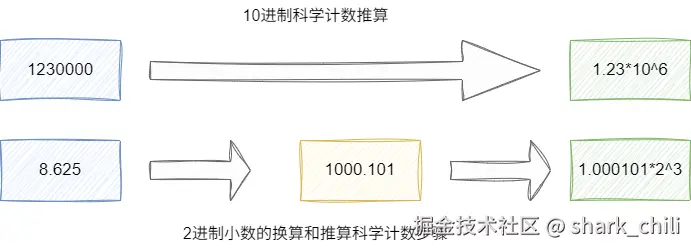
如何用二进制空间表示科学计数法的结果

float使用二进制32位也就是4个字节，double用二进制64位表示也就是8个字节，下图便是它们存储带有小数的数值的内存空间划分，读者可以先行了解一下，后文会针对以float进行推算演示：

我们不妨用10.625作为例子看看将其存到float内存空间是什么样子的，首先我们先进行科学计数演算，对应过程上文已经说明了，这里就不多赘述了，读者可以查阅下图复习一下：

然后看看我的科学计数代入到float进行推算表示：

1. 因为10.625是正数，所以符号位为0
2. 科学计数为*2(^3)，所以指数位为3，但是指数可能存在正负数的情况，计算机为了方便表示都会加一个偏移量127即01111111，例如我们这里的指数为3，那么指数位就是10000010，如果是-3那就表示为01111101
3. 最后是尾数010101由于只有6位，用0填充剩下的18位得010101000000000000000000

最终float结果标识如下：

可能细心的同学会发现整数部分的1没了，回答这个问题也很简单， IEEE 标准规定规格化数的整数部分总是1(像0.5这样的十进制通用1*(2^-1)的二进制数表示)

既然讲了换算成二进制，那么我们就来讲讲怎么还原为十进制吧

1. 高位为0即正数
2. 指数位为130-127=3
3. 尾数为010101可得1/4+1/16+1/64
4. 再加上隐含的1得1.328125
5. 1.328125*8=10.625

详解0.1+0.2==0.3返回false

问题描述

由上面的篇幅，我们大概就知道了0.1+0.2为什么不等于0.3了，我们不妨计算一下 就用float表示 0.1可得

0 01111011 10011001100110011001101

0.2用float存可得

0 01111100 10011001100110011001101 

最终还原的计算结果如下，由于浮点数表示的位数有限，无限循环的二进制小数被截断，导致精度损失：

解决方案

所以我们在使用java进行小数比较计算时建议使用BigDecimal 来解决，因为BigDecimal 通过借助整数来表示小数的方式，举个不恰当的例子即0.1和0.2相加，对应的保留精度的方案为：

1. 小数0.1*10得到1
2. 小数0.2*10得到2
3. 两者相加得到3
4. 换算精度时直接除10得到0.3

因为对于整数而言，二进制和十进制是完全一一对应的，用整数来表示小数，再记录下小数的位数，就可以完美地解决该问题：

BigDecimal num1 = new BigDecimal("0.1");
BigDecimal num2 = new BigDecimal("0.2");
BigDecimal sum = num1.add(num2);
System.out.println("0.1+0.2==0.3 ? res:" + sum.equals(new BigDecimal("0.3")));

编程中运算的一点建议

这里笔者也补充说明一句，在二进制的世界里乘法本质上就是多次加法运算的组合，所以如果明确乘除法计算的情况下，我们尽可能使用位运算避免复杂的算术运算开销，例如下面这段代码，执行21亿次的乘除运算：

int i = 16;
long begin = System.currentTimeMillis();
for (int j = 0; j < Integer.MAX_VALUE; j++) {
    i = i * 4;
    i = i / 4;
}
long end = System.currentTimeMillis();
System.out.println("i:" + i + " cost:" + (end - begin) + "ms");

对应的输出结果如下，耗时大约2s左右：

i:16 cost:1802ms

实际上在二进制运算中乘除4本质上就是左右移位运算，对应的我们将代码改为下面这个样子：

public static void main(String[] args) {
    int i = 16;
    long begin = System.currentTimeMillis();
    for (int j = 0; j < Integer.MAX_VALUE; j++) {
        i = i << 2;
        i = i >> 2;
    }
    long end = System.currentTimeMillis();
    System.out.println("i:" + i + " cost:" + (end - begin) + "ms");
}

此时耗时就变为3ms，原因也很简单，原本乘法运算是基于加法的复杂实现，我们通过规律的寻找将其改为一个简单的移位运算，避免了复杂的算术运算，性能自然提高：

i:16 cost:3ms

小结

本文从CPU的基本构成开始，逐步介绍了计算机如何通过晶体管实现逻辑运算和算术运算。首先介绍了NMOS和PMOS两种晶体管的工作原理，然后基于这些基本元件构建了各种逻辑门电路。通过逻辑门的组合，实现了半加器和全加器，进而构建了完整的算术逻辑单元(ALU)。

接着，文章深入探讨了二进制运算的特点，包括整数和小数的二进制表示方法，重点解释了为什么负数要使用补码表示，以及补码相比原码和反码的优势。此外，还详细分析了浮点数在计算机中的存储方式，以及由此引发的精度问题，特别是0.1+0.2!=0.3这一经典问题的原因和解决方案。

最后，文章还给出了一些编程中的优化建议，如使用位运算替代乘除法运算以提高性能。

通过本文的介绍，读者应该能够理解计算机底层是如何进行数据表示和运算的，以及在实际编程中需要注意的一些数值计算问题。

我是 SharkChili ，Java 开发者，Java Guide 开源项目维护者。欢迎关注我的公众号：写代码的SharkChili ，也欢迎您了解我的开源项目 mini-redis：github.com/shark-ctrl/...

为方便与读者交流，现已创建读者群。关注上方公众号获取我的联系方式，添加时备注加群即可加入。

参考

为什么 0.1 + 0.2 不等于 0.3 ?:xiaolincoding.com/os/1_hardwa... 为什么计算机负数的补码取反后要加一？要加一？要加一?:zhidao.baidu.com/question/19... Java中的小数运算与精度损失:www.cnblogs.com/wunsiang/p/... 区分PMOS管和NMOS管的巧妙记忆方法:blog.csdn.net/tanguohua_6... MOS管的使用方法:blog.csdn.net/Dingjiawang... MOS管基本认识（快速入门）:blog.csdn.net/baidu_19356...

本文使用 markdown.com.cn 排版