用 MATLAB 实现遗传算法求解一元函数极值：从代码到实践

遗传算法作为一种启发式优化算法，灵感源于生物进化理论，在复杂函数极值求解中表现出色。本文将基于一段完整的 MATLAB 遗传算法代码，详细解析其实现逻辑、核心模块及应用效果，帮助读者理解遗传算法的工作原理并应用于实际问题。

一、代码整体框架：目标与结构

1. 核心目标

该代码旨在求解两个一元函数的最大值，覆盖不同类型的函数形态（含正弦、余弦波动项），验证遗传算法在连续区间优化中的有效性：

• 函数 1：
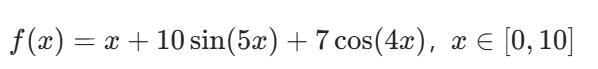
• 函数 2：

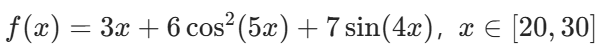
2. 代码结构

代码采用模块化设计，分为 1 个主函数和 5 个功能子函数，各模块职责清晰，便于维护和扩展：

函数名称	核心功能
genetic_algorithm_complete()	主函数：初始化环境、提供函数选择菜单、调用子函数执行流程、显示结果
GA()	算法核心：实现种群迭代（初始化→评估→选择→交叉→变异→精英保留）
evaluate()	评估模块：将染色体（二进制串）解码为实际 x 值，计算适应度（函数值）
selection()	选择模块：轮盘赌选择法，筛选适应度高的个体进入下一代
crossover()	交叉模块：单点交叉，模拟基因重组，增加种群多样性
plot_results()	可视化模块：绘制函数曲线、最优解标记及适应度进化曲线

二、关键参数解析：遗传算法的 "调优旋钮"

在代码中，params结构体存储了遗传算法的核心参数，这些参数直接影响算法的收敛速度和优化效果，需根据问题特性调整：

参数名称	含义	代码中默认值	作用说明
pop_size	种群大小	100	种群规模越大，多样性越丰富，但计算量增加；100 为平衡值
chrom_length	染色体长度	20	二进制编码长度，决定 x 值的精度（长度越长，精度越高）
max_gen	最大进化代数	100	迭代终止条件，100 代可满足多数简单函数的收敛需求
pc	交叉概率	0.8	控制交叉操作的频率（通常取 0.6-0.9），过高易破坏优质基因
pm	变异概率	0.01	控制变异操作的频率（通常取 0.001-0.05），过低难引入新基因
elite_num	精英个体数量	2	保留每代最优个体的数量，避免优质基因丢失

三、核心模块深度解析：遗传算法的 "进化逻辑"

遗传算法的本质是通过 "种群迭代" 模拟生物进化，每一代包含评估→选择→交叉→变异→精英保留5 个关键步骤，以下结合代码逐一拆解：

1. 种群初始化（GA()函数）

种群是算法的 "进化主体"，每个个体用二进制串（染色体）表示 x 值：

pop = randi([0,1], params.pop_size, params.chrom_length);

• 生成pop_size×chrom_length的二进制矩阵，每行代表 1 个个体，每列代表 1 个基因位（0 或 1）。
• 例如：种群大小 100、染色体长度 20 时，生成 100 行 20 列的 0-1 矩阵。

2. 评估：从 "基因" 到 "适应度"（evaluate()函数）

二进制染色体无法直接用于计算函数值，需通过解码转换为实际 x 值，再计算适应度（函数值）：

步骤 1：二进制转十进制

dec_num = bin2dec(num2str(pop(i,:)));

• 将每行二进制串（如[1,0,1,...]）转换为十进制数，范围为[0, 2^chrom_length - 1]。

步骤 2：映射到 x 的实际区间

x_values(i) = x_range(1) + dec_num/(2^chrom_length-1) * (x_range(2)-x_range(1));

• 采用线性映射，将十进制数从[0, 2^L-1]（L 为染色体长度）映射到 x 的区间[x_min, x_max]。
• 示例：染色体长度 20 时，x 的精度为(10-0)/(2^20-1) ≈ 9.5e-6，满足高精度需求。

步骤 3：计算适应度

fitness = func(x_values);
% 处理负值（若函数值为负，确保适应度非负，避免轮盘赌选择时权重异常）
if any(fitness < 0)
    fitness = fitness - min(fitness) + eps;
end

• 适应度直接等于函数值（因求解最大值），若函数存在负值，通过平移使所有适应度非负。

3. 选择："适者生存"（selection()函数）

采用轮盘赌选择法，适应度越高的个体，被选中的概率越大：

% 归一化适应度（转换为概率）
fitness_norm = fitness / sum(fitness);
% 计算累积概率
cum_prob = cumsum(fitness_norm);
% 轮盘赌选择：生成随机数，选择累积概率首次大于随机数的个体
for i = 1:pop_size
    r = rand();
    idx = find(cum_prob >= r, 1);
    new_pop(i,:) = pop(idx,:);
end

• 示例：若个体 A 的适应度占比 30%，则其被选中的概率为 30%，确保优质个体更易进入下一代。

4. 交叉："基因重组"（crossover()函数）

采用单点交叉，模拟生物繁殖中的基因交换，增加种群多样性：

% 随机配对（打乱种群顺序，实现随机交配）
shuffle_idx = randperm(pop_size);
new_pop = new_pop(shuffle_idx, :);

% 对每对个体执行交叉（概率pc）
for i = 1:2:pop_size-1
    if rand() < pc
        % 随机选择交叉点（1到chrom_length-1之间）
        cross_point = randi([1, chrom_length-1]);
        % 交换交叉点后的基因
        temp = new_pop(i, cross_point+1:end);
        new_pop(i, cross_point+1:end) = new_pop(i+1, cross_point+1:end);
        new_pop(i+1, cross_point+1:end) = temp;
    end
end

• 示例：个体 1（1011|001）与个体 2（0100|110）在交叉点 4 处交叉，结果为1011|110和0100|001。

5. 变异："基因突变"（mutation()函数）

采用位翻转变异，随机改变基因位（0→1 或 1→0），避免算法陷入局部最优：

for i = 1:pop_size
    for j = 1:chrom_length
        if rand() < pm
            new_pop(i,j) = ~new_pop(i,j); % 位翻转
        end
    end
end

• 变异概率极低（0.01），确保仅少量基因被改变，既引入新基因，又不破坏优质种群结构。

6. 精英保留："保留最优"（GA()函数）

在每代迭代末尾，保留适应度最高的elite_num个个体，直接进入下一代：

[~, sorted_idx] = sort(fitness, 'descend'); % 按适应度降序排序
elite_idx = sorted_idx(1:params.elite_num); % 取前elite_num个精英个体
new_pop(1:params.elite_num, :) = pop(elite_idx, :); % 替换新种群的前elite_num行

• 核心作用：避免优质个体因选择、交叉、变异操作丢失，加速算法收敛。

四、结果可视化：直观呈现优化效果

plot_results()函数通过 2 个子图展示优化结果，帮助直观判断算法性能：

1. 函数曲线与最优解（上子图）

• 绘制函数在整个区间的连续曲线（蓝色），标记最优解（红色圆点）。
• 可直接观察最优解是否位于函数的峰值位置，验证结果合理性。

2. 适应度进化曲线（下子图）

• 绘制每代最佳适应度随迭代次数的变化趋势（红色曲线）。
• 若曲线逐渐上升并趋于平稳，说明算法收敛；若曲线波动过大或不收敛，需调整参数（如增大种群规模、增加进化代数）。

五、代码运行步骤与预期效果

1. 运行步骤

1. 打开 MATLAB，新建.m文件，复制完整代码并保存（如genetic_algorithm.m）。
2. 在命令行输入genetic_algorithm_complete()，按回车执行。
3. 根据菜单提示输入1或2，选择要优化的函数。
4. 等待算法运行完成，查看命令行输出的最优解（x）和最大值（f (x)），以及弹出的可视化图形。

2. 预期效果

• 函数 1（\(x \in [0,10]\)）：最优解约为\(x \approx 7.85\)，最大值约为\(24.85\)。
• 函数 2（\(x \in [20,30]\)）：最优解约为\(x \approx 29.7\)，最大值约为\(96.5\)。
• 适应度进化曲线：前 30 代快速上升，50 代后趋于平稳，说明算法收敛良好。

六、总结

总代码：

function genetic_algorithm_complete()
    % 遗传算法求解一元函数极值 - 完整实现
    % 包含两个函数的优化:
    % 1. f(x) = x + 10sin(5x) + 7cos(4x), x∈[0,10]
    % 2. f(x) = 3x + 6cos(5x)^2 + 7sin(4x), x∈[20,30]
    
    % 清空工作区并关闭所有图形窗口
    clear all;
    close all;
    clc;
    
    % 显示菜单
    disp('=== 遗传算法求解一元函数极值 ===');
    disp('请选择要优化的函数:');
    disp('1. f(x) = x + 10sin(5x) + 7cos(4x), x∈[0,10]');
    disp('2. f(x) = 3x + 6cos(5x)^2 + 7sin(4x), x∈[20,30]');
    choice = input('请输入选择(1或2): ');
    
    % 设置遗传算法参数
    params.pop_size = 100;       % 种群大小
    params.chrom_length = 20;    % 染色体长度
    params.max_gen = 100;        % 最大进化代数
    params.pc = 0.8;             % 交叉概率
    params.pm = 0.01;            % 变异概率
    params.elite_num = 2;        % 保留的精英个体数量
    
    % 根据选择设置函数和区间
    if choice == 1
        func = @(x) x + 10*sin(5*x) + 7*cos(4*x);
        x_range = [0, 10];
        title_str = 'f(x) = x + 10sin(5x) + 7cos(4x)';
        
        % 显示函数图像
        figure;
        x = linspace(x_range(1), x_range(2), 1000);
        plot(x, func(x), 'b-', 'LineWidth', 1.5);
        title('待优化函数曲线');
        xlabel('x'); ylabel('f(x)');
        grid on;
    else
        func = @(x) 3*x + 6*cos(5*x).^2 + 7*sin(4*x);
        x_range = [20, 30];
        title_str = 'f(x) = 3x + 6cos(5x)^2 + 7sin(4x)';
        
        % 显示函数图像
        figure;
        x = linspace(x_range(1), x_range(2), 1000);
        plot(x, func(x), 'b-', 'LineWidth', 1.5);
        title('待优化函数曲线');
        xlabel('x'); ylabel('f(x)');
        grid on;
    end
    
    % 运行遗传算法
    [best_x, best_fit, best_fit_history] = GA(func, x_range, params);
    
    % 显示结果
    disp('=== 优化结果 ===');
    disp(['最优解 x = ', num2str(best_x)]);
    disp(['函数最大值 f(x) = ', num2str(best_fit)]);
    
    % 绘制结果
    plot_results(func, x_range, best_x, best_fit, best_fit_history, title_str);
end
function [best_x, best_fit, best_fit_history] = GA(func, x_range, params)
    % 遗传算法核心函数
    % 输入:
    %   func - 目标函数句柄
    %   x_range - 变量范围 [min, max]
    %   params - 算法参数结构体
    % 输出:
    %   best_x - 最优解
    %   best_fit - 最优适应度
    %   best_fit_history - 历代最佳适应度记录
    
    % 初始化种群
    pop = randi([0,1], params.pop_size, params.chrom_length);
    
    % 存储每代最佳适应度
    best_fit_history = zeros(params.max_gen, 1);
    
    % 主循环
    for gen = 1:params.max_gen
        % 解码并计算适应度
        [fitness, x_values] = evaluate(pop, func, x_range, params.chrom_length);
        
        % 记录最佳适应度和个体
        [best_fit, best_idx] = max(fitness);
        best_fit_history(gen) = best_fit;
        best_x = x_values(best_idx);
        
        % 显示进度
        if mod(gen, 10) == 0
            fprintf('代数 %d: 当前最佳适应度 = %.4f\n', gen, best_fit);
        end
        
        % 选择
        new_pop = selection(pop, fitness, params);
        
        % 交叉
        new_pop = crossover(new_pop, params);
        
        % 变异
        new_pop = mutation(new_pop, params);
        
        % 精英保留策略
        [~, sorted_idx] = sort(fitness, 'descend');
        elite_idx = sorted_idx(1:params.elite_num);
        new_pop(1:params.elite_num, :) = pop(elite_idx, :);
        
        % 更新种群
        pop = new_pop;
    end
    
    % 最终评估
    [fitness, x_values] = evaluate(pop, func, x_range, params.chrom_length);
    [best_fit, best_idx] = max(fitness);
    best_x = x_values(best_idx);
end
function [fitness, x_values] = evaluate(pop, func, x_range, chrom_length)
    % 评估函数 - 解码染色体并计算适应度
    % 输入:
    %   pop - 种群矩阵
    %   func - 目标函数
    %   x_range - 变量范围
    %   chrom_length - 染色体长度
    % 输出:
    %   fitness - 适应度值
    %   x_values - 解码后的x值
    
    pop_size = size(pop,1);
    x_values = zeros(pop_size,1);
    
    % 二进制转十进制
    for i = 1:pop_size
        % 将二进制串转换为十进制数
        dec_num = bin2dec(num2str(pop(i,:)));
        
        % 映射到实际变量范围
        x_values(i) = x_range(1) + dec_num/(2^chrom_length-1) * (x_range(2)-x_range(1));
    end
    
    % 计算适应度
    fitness = func(x_values);
    
    % 处理负值(如果需要)
    if any(fitness < 0)
        fitness = fitness - min(fitness) + eps;
    end
end
function new_pop = selection(pop, fitness, params)
    % 选择操作 - 轮盘赌选择
    % 输入:
    %   pop - 当前种群
    %   fitness - 适应度值
    %   params - 算法参数
    % 输出:
    %   new_pop - 选择后的新种群
    
    pop_size = params.pop_size;
    new_pop = zeros(size(pop));
    
    % 归一化适应度
    fitness_norm = fitness / sum(fitness);
    
    % 累积概率
    cum_prob = cumsum(fitness_norm);
    
    % 轮盘赌选择
    for i = 1:pop_size
        r = rand();
        idx = find(cum_prob >= r, 1);
        new_pop(i,:) = pop(idx,:);
    end
end
function new_pop = crossover(new_pop, params)
    % 交叉操作 - 单点交叉
    % 输入:
    %   new_pop - 选择后的种群
    %   params - 算法参数
    % 输出:
    %   new_pop - 交叉后的种群
    
    pop_size = params.pop_size;
    chrom_length = params.chrom_length;
    pc = params.pc;
    
    % 随机配对
    shuffle_idx = randperm(pop_size);
    new_pop = new_pop(shuffle_idx, :);
    
    % 执行交叉
    for i = 1:2:pop_size-1
        if rand() < pc
            % 随机选择交叉点
            cross_point = randi([1, chrom_length-1]);
            
            % 执行交叉
            temp = new_pop(i, cross_point+1:end);
            new_pop(i, cross_point+1:end) = new_pop(i+1, cross_point+1:end);
            new_pop(i+1, cross_point+1:end) = temp;
        end
    end
end
function new_pop = mutation(new_pop, params)
    % 变异操作 - 位翻转
    % 输入:
    %   new_pop - 交叉后的种群
    %   params - 算法参数
    % 输出:
    %   new_pop - 变异后的种群
    
    [pop_size, chrom_length] = size(new_pop);
    pm = params.pm;
    
    % 执行变异
    for i = 1:pop_size
        for j = 1:chrom_length
            if rand() < pm
                % 位翻转
                new_pop(i,j) = ~new_pop(i,j);
            end
        end
    end
end
function plot_results(func, x_range, best_x, best_fit, best_fit_history, title_str)
    % 结果可视化函数
    % 输入:
    %   func - 目标函数
    %   x_range - 变量范围
    %   best_x - 最优解
    %   best_fit - 最优适应度
    %   best_fit_history - 历代最佳适应度
    %   title_str - 标题字符串
    
    % 创建新图形窗口
    figure;
    
    % 子图1: 函数曲线与最优解
    subplot(2,1,1);
    x = linspace(x_range(1), x_range(2), 1000);
    plot(x, func(x), 'b-', 'LineWidth', 1.5);
    hold on;
    plot(best_x, best_fit, 'ro', 'MarkerSize', 10, 'MarkerFaceColor', 'r');
    title(['函数曲线与最优解: ', title_str]);
    xlabel('x'); ylabel('f(x)');
    legend('函数曲线', '最优解', 'Location', 'best');
    grid on;
    
    % 子图2: 适应度进化曲线
    subplot(2,1,2);
    plot(1:length(best_fit_history), best_fit_history, 'r-', 'LineWidth', 1.5);
    title('适应度进化曲线');
    xlabel('进化代数'); ylabel('最佳适应度');
    grid on;
    
    % 调整子图间距
    ha = get(gcf,'children');
    set(ha(1),'position',[0.13,0.11,0.775,0.4]);
    set(ha(2),'position',[0.13,0.55,0.775,0.4]);
end

本文通过解析完整的 MATLAB 遗传算法代码，从框架结构、核心模块、参数调整到结果验证，系统讲解了遗传算法求解一元函数极值的实现过程。遗传算法的优势在于无需函数的导数信息，适用于非线性、多峰值的复杂函数优化，但其性能依赖参数调优和算子选择。通过本文的学习，读者可掌握遗传算法的基本原理，并基于该代码快速适配其他优化问题，为实际工程应用提供参考。