题目


说明
这题属于基础知识题,考察点:
1、Fisher线性判别器
2、pytorch构造神经网络架构
知识点
零、Fisher线性判别器:
Fisher 线性判别器(FLD)是由英国统计学家 Ronald Fisher 于 1936 年提出的经典线性判别方法,核心思想是通过一条直线(二维)或一个超平面(高维)将不同类别的数据 "最优分离"------ 即最大化类间差异、最小化类内差异,从而实现对数据的分类。它是模式识别、机器学习领域中线性分类器的基础,也是理解 "降维 + 分类" 融合思路的关键模型。
一、FLD 的核心目标:什么是 "最优线性分离"?
FLD 解决的是二分类问题(多分类可通过 "一对多""一对一" 扩展),其核心逻辑是:将高维数据投影到一条直线(一维空间)上后,让两类数据在投影后的空间中 "分得最开"。
具体来说,"最优分离" 需同时满足两个条件:
- 类间距离最大:两类数据在投影后的 "中心(均值)" 距离尽可能远;
- 类内距离最小:每一类数据在投影后的 "离散程度(方差)" 尽可能小。
举个直观例子:假设两类数据(如 "猫" 和 "狗" 的图像特征)在高维空间中混合分布,FLD 会找到一个投影方向,使得投影后 "猫" 的所有点都集中在一个区域,"狗" 的所有点集中在另一个区域,且两个区域间隔最大 ------ 这样只需在投影后的直线上画一条阈值线,就能轻松区分两类数据。
二、FLD 的数学推导:如何找到 "最优投影方向"?
FLD 的本质是求解一个投影向量 w(高维空间中的直线方向),将高维数据 x(维度为 d)投影到一维空间,投影后的数据为 y=wTx(y 是标量)。推导过程围绕 "最大化目标函数" 展开。
1. 定义核心数学量
首先定义二分类问题中的基础统计量(假设数据分为两类:C1 和 C2):
| 符号 | 含义 |
|---|---|
| N1,N2 | 类别 C1、C2 的样本数量 |
| μ1,μ2 | 类别 C1、C2 在高维空间中的均值向量(维度 d×1) |
| S1,S2 | 类别 C1、C2 的类内散度矩阵(维度 d×d) |
| Sw=S1+S2 | 总类内散度矩阵(衡量两类数据的整体离散程度) |
| Sb=(μ1−μ2)(μ1−μ2)T | 类间散度矩阵(衡量两类均值的差异程度) |
关键矩阵的具体计算
-
类内散度矩阵 Si (描述单个类内样本与类均值的偏离):
对类别 Ci,每个样本 xj∈Ci,则
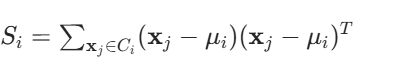
直观理解:Si 越大,说明该类数据在高维空间中越分散。
-
类间散度矩阵 Sb (描述两类均值的差异):
由于 μ1−μ2 是 d×1 向量,其外积 (μ1−μ2)(μ1−μ2)T 是 d×d 矩阵,且秩为 1(仅包含两类均值的差异信息)。
2. 投影后的统计量
当数据通过 w 投影到一维空间后,上述统计量对应变为:
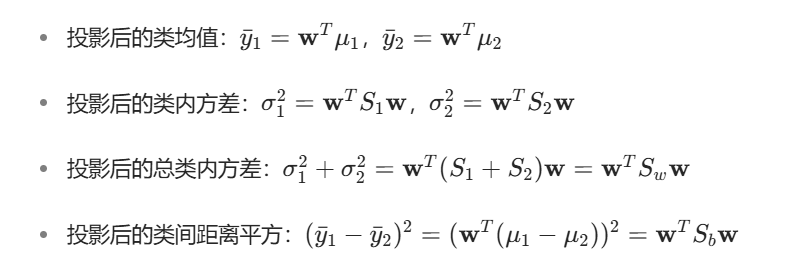
3. Fisher 准则函数:最大化 "类间 / 类内" 比

4. 最优投影向量的最终形式
综上,FLD 的最优投影向量为:
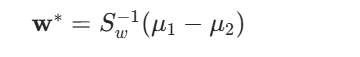
注意:w∗ 的 "方向" 是关键(决定投影效果),其 "长度" 不影响投影结果(因为投影 y=wTx 对 w 成比例缩放后,y 也成比例缩放,类间 / 类内比不变),因此实际应用中无需关注 w∗ 的长度。
三、FLD 的分类流程(完整步骤)
得到最优投影向量 w∗ 后,FLD 的分类过程可分为 3 步:
步骤 1:训练阶段 ------ 计算 w∗ 和分类阈值 y0

步骤 2:测试阶段 ------ 对新样本分类

四、FLD 的特点与局限性
1. 核心优点
- 降维与分类结合:将高维数据投影到一维空间,既简化了计算,又保留了 "最优分离" 的关键信息,适合高维小样本场景(如早期图像识别);
- 理论简洁且可解释:最优投影向量直接由数据的均值和散度矩阵决定,物理意义明确(最大化类间 / 类内比);
- 计算成本低:仅需计算均值、散度矩阵及其逆,无迭代过程,训练速度快。
2. 主要局限性
- 仅支持二分类:FLD 原生是二分类模型,多分类需通过 "一对多"(One-vs-Rest)或 "一对一"(One-vs-One)扩展,且扩展后效果可能下降;
- 假设数据近似正态分布:FLD 隐含 "两类数据服从同协方差矩阵的正态分布" 假设,若数据分布严重偏离正态(如非凸、多峰),分离效果会变差;
- 对异常值敏感:类内散度矩阵 Sw 受异常值影响较大,若训练集中有极端异常值,会导致 Sw 估计偏差,进而影响 w∗ 的准确性;
- 线性可分假设 :FLD 是线性模型,若两类数据在原始空间中非线性可分(如 "异或" 问题),仅通过线性投影无法实现有效分离,此时需结合核方法(如核 Fisher 判别器,Kernel FLD)。
五、FLD 与其他线性分类器的对比
为了更清晰地理解 FLD 的定位,下表对比了 FLD 与逻辑回归(Logistic Regression)、线性支持向量机(Linear SVM)的核心差异:
| 对比维度 | Fisher 线性判别器(FLD) | 逻辑回归(Logistic Regression) | 线性支持向量机(Linear SVM) |
|---|---|---|---|
| 核心目标 | 最大化投影后的类间 / 类内比(基于数据分布) | 最大化分类概率的对数似然(基于概率模型) | 最大化两类样本到超平面的最小距离(间隔最大化) |
| 概率输出 | 无(仅硬分类) | 有(输出属于某类的概率) | 无(原生仅硬分类,可通过 Platt 缩放扩展概率) |
| 处理非线性 | 原生不支持(需核方法扩展) | 原生不支持(需特征映射扩展) | 支持(通过核方法,如 RBF 核) |
| 对样本数量的敏感 | 适合小样本(高维小样本优势明显) | 适合大样本(样本量越大,概率估计越准) | 对样本数量不敏感,但大样本下计算成本高 |
| 应用场景 | 高维小样本、降维优先的分类任务(如早期模式识别) | 需概率解释的分类任务(如风险评估、医疗诊断) | 追求高分类精度、线性可分 / 近似可分场景(如文本分类) |
六、FLD 的扩展与应用
1. 核 Fisher 判别器(Kernel FLD)
为解决 FLD 无法处理非线性数据的问题,核 FLD 引入核方法:通过核函数(如 RBF 核、多项式核)将原始高维数据映射到更高维的特征空间,在特征空间中构建线性 FLD,从而实现对原始空间中非线性数据的分离。核 FLD 保留了 FLD 的简洁性,同时提升了对非线性数据的适应能力。
2. 典型应用场景
- 早期模式识别:如手写数字识别(MNIST 数据集的早期基线模型)、字符分类;
- 生物特征识别:如人脸识别(将人脸图像的高维像素特征投影到一维,实现身份验证);
- 高维小样本数据分类:如基因数据、光谱数据的分类(样本量少但维度极高,FLD 的降维优势可充分发挥)。
七、总结
Fisher 线性判别器是线性分类与降维领域的经典模型,其核心思想 "最大化类间差异、最小化类内差异" 为后续的判别式模型(如 SVM)奠定了基础。尽管 FLD 存在 "仅支持二分类""线性可分假设" 等局限性,但在高维小样本、数据近似正态分布的场景中,仍具有不可替代的优势。
理解 FLD 的推导过程(尤其是 Fisher 准则函数与瑞利商的关系),不仅能掌握其应用方法,更能深入理解 "判别式学习" 的核心逻辑 ------ 从数据的统计特性出发,直接优化分类性能,而非先建模数据分布(生成式模型思路)。
代码
python
import numpy as np
import json
from typing import Tuple, List
class FisherLDA:
"""
Fisher线性判别分析(Linear Discriminant Analysis, LDA)实现
用于二分类问题的降维和分类
"""
def __init__(self, reg_param: float = 1e-6):
"""
初始化LDA分类器
Args:
reg_param: 正则化参数,用于避免奇异矩阵
"""
self.reg_param = reg_param
self.w = None # 投影向量
self.mu0 = None # 类别0的均值
self.mu1 = None # 类别1的均值
self.m0 = None # 训练集中类别0的投影均值
self.m1 = None # 训练集中类别1的投影均值
def _compute_class_means(self, X: np.ndarray, y: np.ndarray) -> Tuple[np.ndarray, np.ndarray]:
"""
计算各类别的均值向量
Args:
X: 特征矩阵 (n_samples, n_features)
y: 标签向量 (n_samples,)
Returns:
mu0, mu1: 两个类别的均值向量
"""
# 类别0的样本
X0 = X[y == 0]
N0 = len(X0)
mu0 = np.sum(X0, axis=0) / N0 if N0 > 0 else np.zeros(X.shape[1])
# 类别1的样本
X1 = X[y == 1]
N1 = len(X1)
mu1 = np.sum(X1, axis=0) / N1 if N1 > 0 else np.zeros(X.shape[1])
return mu0, mu1
def _compute_within_class_scatter(self, X: np.ndarray, y: np.ndarray,
mu0: np.ndarray, mu1: np.ndarray) -> np.ndarray:
"""
计算类内散度矩阵 S_W
Args:
X: 特征矩阵
y: 标签向量
mu0, mu1: 两个类别的均值向量
Returns:
S_W: 类内散度矩阵
"""
n_features = X.shape[1]
S_W = np.zeros((n_features, n_features))
# 计算类别0的散度
for i in range(len(X)):
if y[i] == 0:
diff = (X[i] - mu0).reshape(-1, 1)
S_W += diff @ diff.T
elif y[i] == 1:
diff = (X[i] - mu1).reshape(-1, 1)
S_W += diff @ diff.T
return S_W
def fit(self, X: np.ndarray, y: np.ndarray):
"""
训练LDA模型
Args:
X: 训练特征矩阵 (n_samples, n_features)
y: 训练标签向量 (n_samples,), 值为0或1
"""
# 1. 计算类别均值
self.mu0, self.mu1 = self._compute_class_means(X, y)
# 2. 计算类内散度矩阵
S_W = self._compute_within_class_scatter(X, y, self.mu0, self.mu1)
# 3. 添加正则化项避免奇异
S_W_reg = S_W + self.reg_param * np.eye(S_W.shape[0])
# 4. 计算投影向量 w = (S_W_reg)^(-1) * (mu1 - mu0)
try:
self.w = np.linalg.solve(S_W_reg, (self.mu1 - self.mu0))
except np.linalg.LinAlgError:
# 如果仍然奇异,使用伪逆
self.w = np.linalg.pinv(S_W_reg) @ (self.mu1 - self.mu0)
# 5. 计算训练集中两类的投影均值
self.m0 = self.w.T @ self.mu0
self.m1 = self.w.T @ self.mu1
def predict(self, X: np.ndarray) -> np.ndarray:
"""
对测试样本进行预测
Args:
X: 测试特征矩阵 (n_samples, n_features)
Returns:
predictions: 预测标签 (n_samples,)
"""
if self.w is None:
raise ValueError("模型尚未训练,请先调用fit方法")
# 将样本投影到一维
z = X @ self.w
# 分类规则:比较与两类投影均值的距离
predictions = np.zeros(len(X), dtype=int)
for i in range(len(X)):
dist_to_class0 = abs(z[i] - self.m0)
dist_to_class1 = abs(z[i] - self.m1)
predictions[i] = 1 if dist_to_class1 < dist_to_class0 else 0
return predictions
def parse_input(input_str: str) -> Tuple[np.ndarray, np.ndarray, np.ndarray]:
"""
解析JSON格式的输入数据
Args:
input_str: JSON格式的输入字符串
Returns:
X_train, y_train, X_test: 训练特征、训练标签、测试特征
"""
data = json.loads(input_str.strip())
# 解析训练数据
train_data = np.array(data['train'])
X_train = train_data[:, :-1] # 前m列为特征
y_train = train_data[:, -1].astype(int) # 最后一列为标签
# 解析测试数据
X_test = np.array(data['test'])
return X_train, y_train, X_test
def main():
"""
主函数:读取输入,训练模型,输出预测结果
"""
# 读取输入
input_str = input().strip()
try:
# 解析数据
X_train, y_train, X_test = parse_input(input_str)
# 创建并训练LDA模型
lda = FisherLDA(reg_param=1e-6)
lda.fit(X_train, y_train)
# 预测测试样本
predictions = lda.predict(X_test)
# 输出结果
result = predictions.tolist()
print(json.dumps(result))
except Exception as e:
# 错误处理
print(f"错误: {str(e)}")
return
if __name__ == "__main__":
main()