区间DP .

什么是区间DP

区间DP的特点：

• 可以将一个大区间的问题拆成若干个子区间合并的问题
• 两个连续的子区间可以进行整合、合并成一个大区间

区间DP一般遵循以下方法：

普通区间DP

例题1：石子合并

link:2.石子合并 - 蓝桥云课

code1:dfs + 记忆化搜索

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MAXN = 200 + 7;
const ll inf = 0x3f3f3f3f;
ll n, a[MAXN], sum[MAXN], dp[MAXN][MAXN];// dp[i][j]表示a[i~ j] (闭区间)对应合并最小花费

ll dfs(ll l, ll r)
{
    if(dp[l][r] != -1) return dp[l][r];
    ll ret = inf;
    if(l > r)
    {
        return inf;
    }
    if(l == r) 
    {
        ret = 0;
    }
    else if(l + 1 == r)
    {
        ret = a[l] + a[r];
    }
    else
    {
        for(int k = l ; k + 1 <= r; k++)
        {
            ret = min(ret, dfs(l, k) + dfs(k+1ll, r) + sum[r] - sum[l - 1]);
        }
    }
    dp[l][r] = ret;
    return ret;
}

int main()
{
    // input
    cin>>n;
    for(int i = 1; i <= n; i++) cin>>a[i], sum[i] = sum[i - 1] + a[i];
    // init dp
    for(int i = 0; i < MAXN; i++)
        for(int j = 0; j < MAXN; j++)
            dp[i][j] = -1;
    // dfs
    ll ans = dfs(1, n);
    cout<<ans<<endl;
    return 0;
}

code2：DP

错误转移code，先枚举起点：

正确转移code，先由小到大枚举len：

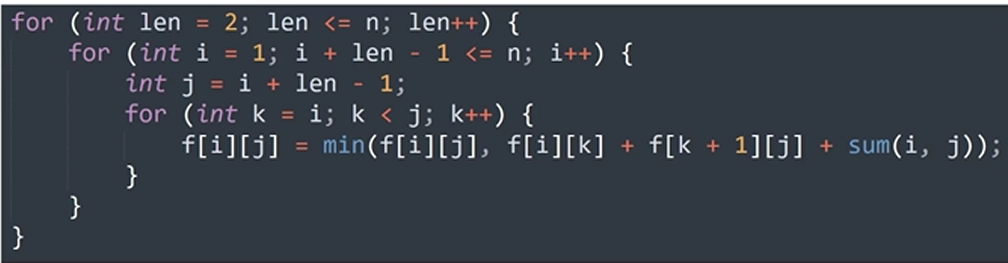
例题2：涂色

link:1.涂色 - 蓝桥云课

分析：

状态表示：dplr表示stri\~r对应的涂色最少步骤

状态转移（f即dp数组）：

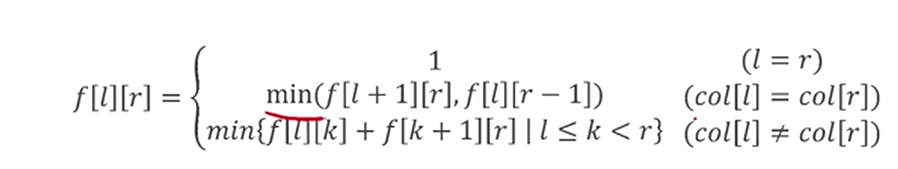
code(DP)

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const ll MAXN = 50 + 7;
ll dp[MAXN][MAXN];

string str;

int main()
{
    cin>>str;
    int sz = str.size();
    // init dp
    memset(dp, 0x3f, sizeof dp);
    for(int i = 0; i < sz; i++) dp[i][i] = 1;

    // dp
    for(int len = 2; len <= sz; len++)
        for(int l = 0, r = l + len - 1; r <= sz -1; l++, r = l + len - 1)
            for(int k = l; k + 1 <= r; k++)
            {
                if(str[l] == str[r]) dp[l][r] = min(dp[l][r-1], dp[l + 1][r]);
                //dp[l][r-1], dp[l + 1][r]两者相等，任选一个也可。
                else dp[l][r] = min(dp[l][r], dp[l][k] + dp[k + 1][r]);
            }
    cout<<dp[0][sz - 1]<<endl;
    return 0;
}

tips

• 本题的难点是子区间合并时可能出现两端相同的特殊情况，如AAAAA,或AGRGA,此时若按dp04 = min(dp0k + dpk + 14)进行状态转移，就会出错。
• 解决此难点也很简单，只要将两端相同情况转化为两端不同情况就可以继续使用dplr = min(dplk + dpk + 1r)进行状态转移了
• 解决此问题时，我们不必关心子问题如何解决（如AGRG拆分成A与GRG时，GRG是否能够计算正确），区间DP与dfs一样，我们只需用关心如何由子问题转移到此问题即可，而不用关心子问题是否正确。

例题3：制作回文串

link:1.制作回文串 - 蓝桥云课

分析：

• 合并两个子区间时，如ABCD 与E，最后回文串一定是删除右端E或左端新加一个E（选择花费最少的方案），不可能是将ABCD对应的回文串的左端修改为E（修改其他字符为E的花费大于直接新加一个E）
• 当前区间字符串两端字符不相等时，dplr一定是从dpir-1或dpl+1r转移过来的，因为两端字符一定有且只有一个被增加/删除；

code(DP)

#include <bits/stdc++.h>
using namespace std;
using ll = long long;
ll cost[26 + 200], dp[2007][2007];

int main()
{
    // input
    ll N, M; cin>>N>>M;
    string S;cin>>S;
    for(int i = 1; i <= N; i++)
    {
        char ch;ll x,y; cin>>ch>>x>>y;
        cost[ch] = min(x, y);
    }
    // dp
    for(int len = 2; len <= M; len++)
        for(int l = 0; l + len - 1 <= M - 1; l++)
        {
            ll r = l + len - 1;
            if(S[l] == S[r])
            {
                if(len == 2)dp[l][r] = 0;
                else dp[l][r] = dp[l + 1][r - 1];
            }
            else
            {
                dp[l][r] = min(cost[S[l]] + dp[l+1][r], dp[l][r - 1] + cost[S[r]]);
            }
        }
    cout<<dp[0][M-1]<<endl;
    return 0;
}

环形区间DP

什么是环形区间DP

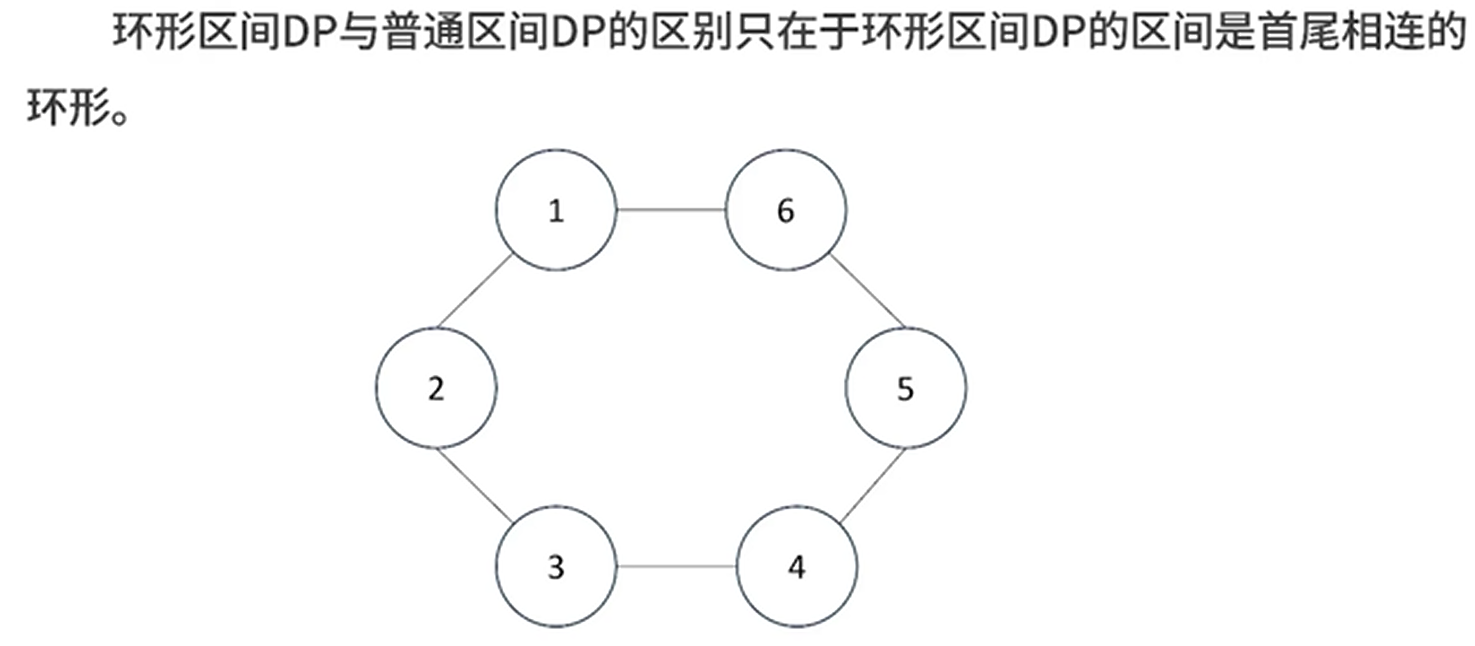
环形区间DP要点：

• 数据的处理方法是将原区间复制一份在后边,总长度×2。
• 枚举的方法与普通区间DP一致。
• 统计答案时要枚举所有的答案区间,找出最优答案。

例题4：能量项链

link:1.能量项链 - 蓝桥云课

本题和例1没有任何区别,只是区间变成了环形,代价变成了首尾乘积,

code

#include <bits/stdc++.h>
using namespace std;
int hd[107 * 2], dp[107*2][107*2];

int main()
{
    int N; cin>>N;
    for(int i = 1; i <= N; i++) cin>>hd[i];
    for(int i = 1; i <= N; i++) hd[i+N] = hd[i];
    // dp
    for(int len = 2; len <= N; len++)
        for(int l = 1; l + len - 1 <= 2 * N; l++)
        {
            int r = l + len - 1;
            for(int k = l; k <= r - 1; k++)
            {
                dp[l][r] = max(dp[l][r], dp[l][k] + dp[k + 1][r] + hd[l] * hd[k + 1] * hd[r + 1]);
            }
        }
    int ans = 0;
    for(int bg = 1; bg <= N; bg++)
    {
        ans = max(ans, dp[bg][bg + N - 1]);
    }
    cout<<ans<<endl;
    return 0;
}