引言
本篇主要介绍不定长滑动窗口 ,如果没有特别说明,后文中的滑动窗口 都指的是不定长滑动窗口。
本篇将介绍滑动窗口的三种题型。
基础部分:专题一 与 专题二 将介绍滑动窗口的用法及原理。
提高部分:专题三 是专题一和专题二的延伸内容。
专题一:求最长子数组
例1.1 无重复字符的最长子串
题目链接:3. 无重复字符的最长子串

暴力解法
直接枚举所有子串:固定子串的的左端点,枚举右端点。
更具体地,令字符串s的长度n,暴力枚举区间:
[0,0]、[0,1]、[0,2]、... [0, n-1],
[1,1]、[1,2]、[1,3]、... [1, n-1],
[2,2]、[2,3]、[2,4]、... [2, n-1],
...,
[n-1,n-1]]。
用哈希表判断[i,j]区间的子串中是否有重复字符。
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = 0;
// 固定左端点。从0开始
for(int l = 0; l < s.size(); l++)
{
int cnt[128]{}; // cnt[i]记录i出现的次数
// 枚举右端点。从l开始
for(int r = l; r < s.size(); r++)
{
cnt[s[r]]++;
// 判断[l, r]区间的子串是否不含有重复字符
bool ok = true;
for(int i = 0; i < 128; i++)
if(cnt[i] > 1)
{
ok = false;
break;
}
if(ok)
len = max(len, r - l + 1);
}
}
return len;
}
};优化1
若[l, r]区间有重复字符,还有必要枚举[l, r+1]、[l, r+2]、...[l, n-1]区间吗?
完全没必要!若[l,r]区间有重复字符,那么显然[l, r+1]、[l, r+2]、...[l, n-1]区间的子串,必定也有重复字符!
该优化我更喜欢称为 可行性剪枝。
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = 0;
for(int l = 0; l < s.size(); l++)
{
int cnt[128]{}; // cnt[i]记录i出现的次数
for(int r = l; r < s.size(); r++)
{
cnt[s[r]]++;
// 判断[l, r]区间的子串是否不含有重复字符
bool ok = true;
for(int i = 0; i < 128; i++)
if(cnt[i] > 1)
{
ok = false;
break;
}
if(ok)
len = max(len, r - l + 1);
else
break; // 第一次不满足条件直接break
//本质上是排除了[l, r], [l, r+1], [l, r+2], ... [l, s.size()-1]区间的子串。
}
}
return len;
}
};对于区间[l, r],我们有没有必要每次都要遍历cnt数组呢?
其实没有必要,如果不满足条件,那么必定是最右端的字符s[r]破坏了条件!
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = 0;
for(int l = 0; l < s.size(); l++)
{
int cnt[128]{}; // cnt[i]记录i出现的次数
for(int r = l; r < s.size(); r++)
{
cnt[s[r]]++;
if(cnt[s[r]] > 1) break; // 只需判断最右端的即可
len = max(len, r - l + 1);
}
}
return len;
}
};优化2
break后,l往后移动至l+1,r从l+1开始往后枚举。 r有必要从l+1开始枚举吗?
其实也没必要。因为若[l,r]触发了break,由于r是从前往后枚举的,那说明[l,r-1]是满足要求的 ,此时子串长度为r-l。而[l+1,l+1]、[l+1,l+2]、... [l+1,r-1]区间的子串长度都小于r-l,那么这些区间绝对不可能是答案!因此,r可以保持不变!没必要回退至l+1。
该优化我更喜欢称为 最优性剪枝。
上述两个优化加上后,对于示例一:
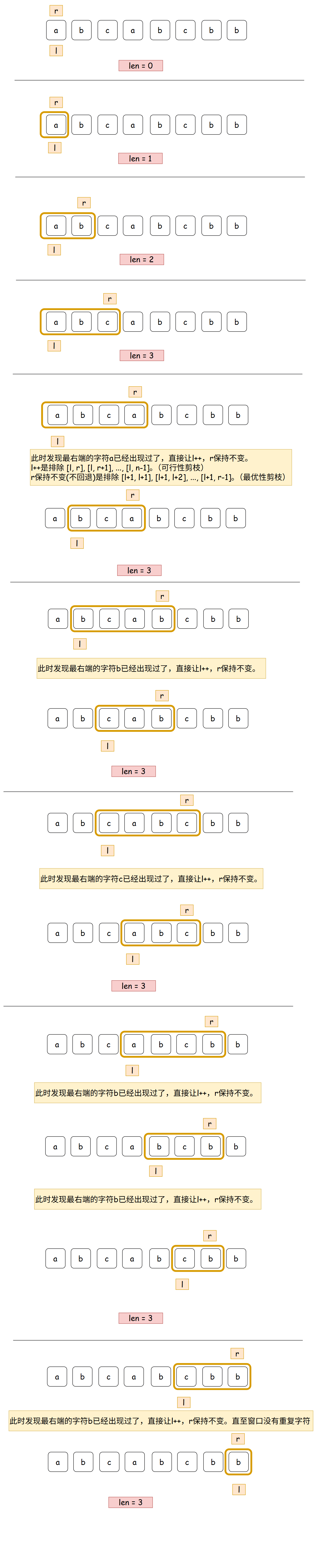
代码如下:
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s) {
int len = 0;
int cnt[128]{};
for(int l = 0, r = 0; r < s.size(); r++)
{
cnt[s[r]]++;
while(cnt[s[r]] > 1) // 不满足要求,这里l++,然后r不回退。
{
cnt[s[l]]--; // 注意需维护cnt数组
l++;
}
len = max(len, r - l + 1);
}
return len;
}
};优化2的代码其实就是滑动窗口的解法,时间复杂度为 O ( N ) O(N) O(N),因为每个字符最多进窗口一次、出窗口一次。
例1.2 水果成篮
题目链接:904. 水果成篮

题意简化:求fruits的最长子数组,需满足:子数组的不同的元素个数不超过 2
暴力解法
直接枚举所有子数组:固定子串的的左端点,枚举右端点。
cpp
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int res = 0;
for(int l = 0; l < fruits.size(); l++)
{
unordered_map<int, int> h; // h[i]记录i的个数
for(int r = l; r < fruits.size(); r++)
{
h[fruits[r]]++;
if(h.size() <= 2)
res = max(res, r - l + 1);
}
}
return res;
}
};优化1
可行性剪枝 :若[l, r]区间不同的元素个数超过2,那就没必要枚举[l, r+1]、[l, r+2]、...[l, fruits.size()-1]区间了。(因为那些区间的元素个数也必定超过 2)
cpp
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int res = 0;
for(int l = 0; l < fruits.size(); l++)
{
unordered_map<int, int> h; // h[i]记录i的个数
for(int r = l; r < fruits.size(); r++)
{
h[fruits[r]]++;
if(h.size() <= 2)
res = max(res, r - l + 1);
else
break; // 第一次超过2时,直接break
}
}
return res;
}
};优化2
最优性剪枝 :break后,l往后移动至l+1, r没必要从l+1开始枚举,保持不变即可。(本质上是排除区间 [l+1, l+1], [l+1, l+2], ..., [l+1, r-1],因为这些区间都被 [l, r-1] 优化掉了)
cpp
class Solution {
public:
int totalFruit(vector<int>& fruits) {
int res = 0;
unordered_map<int, int> h; // h[i]记录i的个数
for(int l = 0, r = 0; r < fruits.size(); r++)
{
h[fruits[r]]++;
while(h.size() > 2)
{
h[fruits[l]]--;
if(h[fruits[l]] == 0)
h.erase(fruits[l]);
l++;
}
res = max(res, r - l + 1);
}
return res;
}
};上面两个例题介绍完毕,想必你已经对滑动窗口有了初步认识。下面给出该类型题目的模板:
模板 ------ 求最长子数组
这种类型的题目一般都是给你一个数组 a r r arr arr,然后求 a r r arr arr 的满足某种性质 的最长 子数组,该性质 必定具备以下特点(在后文中统称为特点1):
特点1
对于区间 [ l , r ] [l,r] [l,r] 与 [ L , R ] [L,R] [L,R], L ≤ l L \le l L≤l, R ≥ r R \ge r R≥r,则有:
- 若 [ l , r ] [l, r] [l,r] 区间的子数组不满足性质 ,那么 [ L , R ] [L, R] [L,R] 区间的子数组也不满足性质。
例如:例1.1 所求的子数组的性质:没有重复字符,该性质具备特点1。例1.2 所求的子数组的性质:不同的元素个数不超过 2 2 2,该性质具备特点1。
模板
cpp
// 初始时l、r都为0
for(int l = 0, r = 0; r < arr.size(); r++)
{
arr[r]进窗口
// 维护窗口
while(窗口不满足性质) // 有些时候需写成:while(l <= r && 窗口不满足性质)
{
arr[l]出窗口
l++;
}
更新答案
}重要结论
更新答案时, [ l , r ] [l, r] [l,r] 是以 r r r 为右端点的所有子数组中,满足性质 且长度最长 的那个。(若 l > r l > r l>r, 说明以 r r r 为右端点的所有子数组中,没有满足性质的)
上述结论可以用数学归纳法 + 反证法 证明(了解即可):
初始时, l l l, r r r 均为 0 0 0,然后 a r r [ r ] arr[r] arr[r] 进窗口,分情况讨论:
- 若 a r r [ r ] arr[r] arr[r] 进窗口后该窗口满足性质,那么显然 [ l , r ] [l, r] [l,r] 其实是以 r r r 为右端点的所有子数组中满足性质 且长度最长的那个。
- 若 a r r [ r ] arr[r] arr[r] 进窗口后该窗口不满足性质,那么下一轮 f o r for for 循环开始时 l l l, r r r 均从 1 1 1 开始,其实又回到了初始阶段。
假设 [ l , r ] [l, r] [l,r] 是以 r r r 为右端点的最长满足性质的子数组,那么进行下一轮循环时,会先把 a r r [ r + 1 ] arr[r+1] arr[r+1] 入窗口,分两种情况讨论:
-
l , r + 1 \] \[l, r+1\] \[l,r+1\] 不满足性质:由于该性质的特点可知: \[ l − d , r + 1 \] \[l-d, r+1\] \[l−d,r+1\] 都不满足该性质,其中 d ≥ 0 d \\ge 0 d≥0。 w h i l e while while 循环结束后,该窗口就是以 r + 1 r+1 r+1 为右端点的最长满足性质的子数组。
滑动窗口正确性回顾:
l++是排除区间[l, r]、[l,r+1]、[l, r+2] ... [l, arr.size()-1],其正确性可以用特点1证明。(可行性剪枝)r不回退是排除区间[l+1, l+1]、[l+1,l+2]、... [l+1,r-1],因为这些区间都被[l, r-1]优化掉了。(最优性剪枝)
注:如果该性质不满足特点1,那就不能用滑动窗口。例如 525. 连续数组,该题的性质是:0的数量跟1的数量相等,该性质不满足特点1,用滑动窗口就会出错。
例题1.3 最大连续1的个数 III
题目链接:1004. 最大连续1的个数 III

可以根据上述例题的解题步骤一步步分析,暴力解法 -> 优化1 -> 优化2。这里直接给出滑动窗口的解法。
问题就相当于:求nums的最长子数组,性质:子数组的0的个数不超过k。
cpp
class Solution {
public:
int longestOnes(vector<int>& nums, int k) {
int res = 0, cnt0 = 0; // cnt0记录0的个数
for(int l = 0, r = 0; r < nums.size(); r++)
{
// nums[r]进窗口
if(nums[r] == 0) cnt0++;
// 维护窗口
while(cnt0 > k)
{
// nums[l]出窗口
if(nums[l] == 0) cnt0--;
l++;
}
// 更新答案
res = max(res, r - l + 1);
}
return res;
}
};例题1.4 每种字符至少取 K 个
题目链接:2516. 每种字符至少取 K 个

此题让求 两端 的最短子数组,满足子数组的 a a a、 b b b、 c c c 的元素个数至少为 k k k。
正难则反,考虑把 两端 转化为 中间 :
令 s s s 中 a a a、 b b b、 c c c 的个数分别为 s u m [ a ] 、 s u m [ b ] 、 s u m [ c ] sum[a]、sum[b]、sum[c] sum[a]、sum[b]、sum[c],对于 a a a,有:
- 两端 的 a a a 的个数 + + + 中间 的 a a a 的个数 = s u m [ a ] = sum[a] =sum[a]
由于两端 的 a a a 的个数 ≥ k \ge k ≥k,所以中间 的 a a a 的个数 ≤ s u m [ a ] − k \le sum[a]-k ≤sum[a]−k。
那么问题可以转换为:求中间的最长 子数组,性质:子数组的 a a a 的个数 ≤ s u m [ a ] − k \le sum[a]-k ≤sum[a]−k 且 b b b 的个数 ≤ s u m [ b ] − k \le sum[b]-k ≤sum[b]−k 且 c c c 的个数 ≤ s u m [ c ] − k \le sum[c]-k ≤sum[c]−k 。
最终答案即为: s . s i z e ( ) s.size() s.size() 减去中间的最长子数组的长度
cpp
class Solution {
public:
int takeCharacters(string s, int k) {
int sum[3]{}, res = 0; // sum[0]、sum[1]、sum[2]分别表示s的a、b、c的个数
for(auto e : s) sum[e - 'a']++;
// 特判s中某个字符数量不足k的情况
if(sum[0] < k || sum[1] < k || sum[2] < k)
return -1;
int cnt[3]{}; // cnt[0]、cnt[1]、cnt[2]分别表示子串[l,r]的a、b、c的个数
for(int l = 0, r = 0; r < s.size(); r++)
{
// s[r]入窗口
int e = s[r] - 'a';
cnt[e]++;
// 维护窗口
while(cnt[e] > sum[e] - k)
{
cnt[s[l] - 'a']--;
l++;
}
// 更新答案
res = max(res, r - l + 1);
}
return s.size() - res;
}
};专题二:求最短子数组
例2.1 长度最小的子数组
题目链接:209. 长度最小的子数组

题目大意:求最短子数组,性质:子数组的所有元素和 ≥ t a r g e t \ge target ≥target
暴力解法
直接枚举所有子数组求解
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int res = nums.size() + 1;
for(int l = 0; l < nums.size(); l++)
{
int sum = 0;
for(int r = l; r < nums.size(); r++)
{
sum += nums[r];
if(sum >= target)
res = min(res, r - l + 1);
}
}
return res == nums.size() + 1 ? 0 : res;
}
};优化1
最优性剪枝 :若[l, r]区间的所有元素和 ≥ t a r g e t \ge target ≥target,就没必要枚举[l, r+1]、[l, r+2]、... [l,n-1]了。(因为题目求的是最短子数组)
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int res = nums.size() + 1;
for(int l = 0; l < nums.size(); l++)
{
int sum = 0;
for(int r = l; r < nums.size(); r++)
{
sum += nums[r];
if(sum >= target)
{
res = min(res, r - l + 1);
break; // 注意:第一次满足条件时才break。(而专题一是第一次不满足条件才break)
}
}
}
return res == nums.size() + 1 ? 0 : res;
}
};优化2
可行性剪枝 :break后,l往后移动至l+1,r没必要l+1开始往后枚举,保持不变即可。
因为触发break时,说明[l,r]是第一次满足元素和 ≥ \ge ≥ target 的,那么 [l,r-1]的元素和必定小于 target 。由于元素均为正整数,那么区间[l+1, l+1]、[l+1,l+2]、... [l+1,r-1]的元素和一定也小于 target 。因此 r 保持不变即可。
上述两个优化加上后,对于示例一:
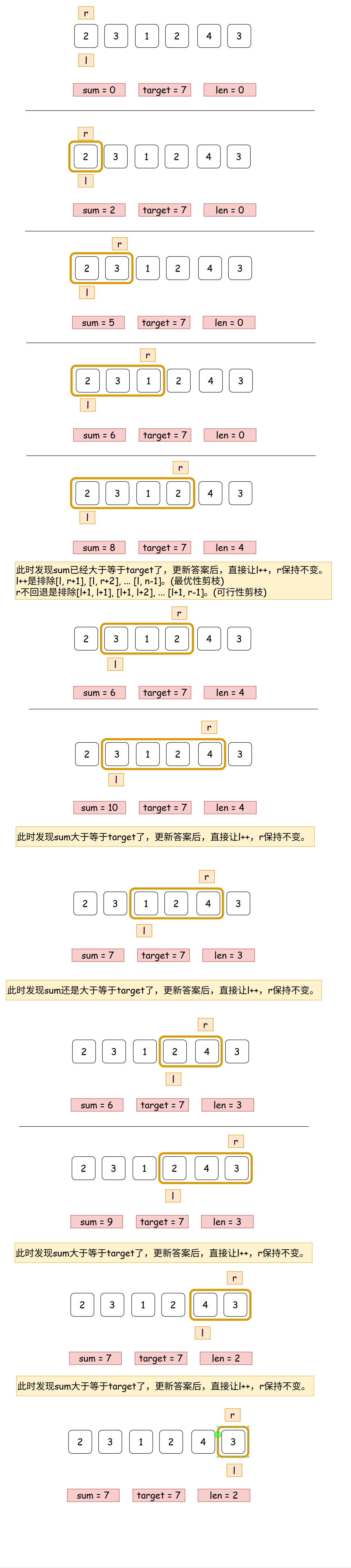
优化后用双指针实现:
cpp
class Solution {
public:
int minSubArrayLen(int target, vector<int>& nums) {
int len = nums.size() + 1, sum = 0;
for(int l = 0, r = 0; r < nums.size(); r++)
{
sum += nums[r];
while(sum >= target)
{
len = min(len, r - l + 1);
sum -= nums[l];
l++;
}
}
return len == nums.size() + 1 ? 0 : len;
}
};模板 ------ 求最短子数组
这种类型的题目一般都是给你一个数组 a r r arr arr,然后求 a r r arr arr 的满足某种性质 的最短 子数组,该性质 必定具备以下特点(在后文中统称为特点2):
特点2
对于区间 [ l , r ] [l,r] [l,r] 与 [ L , R ] [L,R] [L,R], L ≤ l L \le l L≤l, R ≥ r R \ge r R≥r,则有:
- 若 [ L , R ] [L, R] [L,R]区间的子数组不满足性质 ,那么 [ l , r ] [l, r] [l,r]区间的子数组也不满足性质。
例2.1 所求的子数组的性质就是:元素和 ≥ t a r g e t \ge target ≥target,由于元素均为正整数,该性质具备特点2。
模板
cpp
// 初始时l、r都为0
for(int l = 0, r = 0; r < arr.size(); r++)
{
arr[r]入窗口
while(窗口满足性质) // 注意与专题一的模板的区别
{
更新答案 // 在while内部更新答案
arr[l]出窗口
l++;
}
}重要结论
w h i l e while while 循环结束后, [ l − 1 , r ] [l-1, r] [l−1,r] 是以 r r r 为右端点的所有子数组中,满足性质 且长度短 的那个。(若 l l l 为 0 0 0,说明以 r r r 为右端点的所有子数组中,没有能满足性质的)
该结论的证明过程与专题一的类似。
滑动窗口正确性回顾:
l++其实就是排除区间[l,r+1]、[l, r+2] ... [l, arr.size()-1]。因为求的是最短 ,这些区间都被[l, r]优化掉了。(最优性剪枝)r不回退其实就是排除区间[l+1, l+1]、[l+1,l+2]、... [l+1,r-1]。因为[l,r-1]不满足性质,根据特点2,可以证明这些区间都不满足性质。(可行性剪枝)
例2.2 最小覆盖子串
题目链接:76. 最小覆盖子串

题目大意:求 s 的最长子串,性质:子串包含 t 的所有字符 。
如何判断一个子串是否包含 t 的所有字符?
若该子串的每个字符的出现次数都大于等于 t 中对应的字符的出现次数,就可以断定该子串包含 t 的所有字符。
暴力解法
cpp
class Solution {
public:
string minWindow(string s, string t) {
int cnt_t[128]{}; // 记录t中每个字符的个数
for(auto e : t) cnt_t[e]++;
int start = -1, len = s.size() + 1; // start记录答案子串的起始下标,len记录该子串的长度
for(int l = 0; l < s.size(); l++)
{
int cnt[128]{}; // 维护滑动窗口中每个字符的个数
for(int r = l; r < s.size(); r++)
{
cnt[s[r]]++;
// 判断[l, r]是否包含t的所有字符
if(check(cnt, cnt_t))
{
// 更新答案
if(r - l + 1 < len)
{
len = r - l + 1;
start = l;
}
}
}
}
if(len > s.size()) return "";
return s.substr(start, len);
}
// 判断子串是否包含t的所有字符
bool check(int* cnt, int* cnt_t)
{
for(int i = 0; i < 128; i++)
if(cnt[i] < cnt_t[i])
return false;
return true;
}
};优化1
最优性剪枝 :若 [l, r] 已经包含 t 的所有字符了,就没必要枚举 [l, r+1]、[l, r+2]、... [l, s.size()-1] 了。(题目求的是最短 子串,那些区间都被 [l, r] 优化掉了)
cpp
class Solution {
public:
string minWindow(string s, string t) {
int cnt_t[128]{};
for(auto e : t) cnt_t[e]++;
int start = -1, len = s.size() + 1;
for(int l = 0; l < s.size(); l++)
{
int cnt[128]{};
for(int r = l; r < s.size(); r++)
{
cnt[s[r]]++;
if(check(cnt, cnt_t))
{
if(r - l + 1 < len)
{
len = r - l + 1;
start = l;
}
break; // 优化1,没必要继续往后了
}
}
}
if(len > s.size()) return "";
return s.substr(start, len);
}
bool check(int* cnt, int* cnt_t)
{
for(int i = 0; i < 128; i++)
if(cnt[i] < cnt_t[i])
return false;
return true;
}
};优化2
可行性剪枝 :break后,l往后移动至l+1, r没必要从l+1开始枚举,保持不变即可。
因为触发break时,说明[l,r]是第一次满足性质的 ,说明[l,r-1]一定不满足,即[l,r-1]不能包含t的所有字符!那么区间[l+1, l+1]、[l+1,l+2]、... [l+1,r-1]也一定不能包含t的所有字符!所以r没必要回退。
cpp
class Solution {
public:
string minWindow(string s, string t) {
int cnt_t[128]{}; // 记录t中每个字符的个数
for(auto e : t) cnt_t[e]++;
int cnt[128]{}; // 维护滑动窗口中每个字符的个数
int start = -1, len = s.size() + 1; // start记录起始位置,len记录子串长度
for(int l = 0, r = 0; r < s.size(); r++)
{
cnt[s[r]]++; // s[r]入窗口
// 维护窗口
while(check(cnt, cnt_t))
{
if(r - l + 1 < len) // 更新答案
{
len = r - l + 1;
start = l;
}
// s[l]出窗口
cnt[s[l]]--;
l++;
}
}
if(len > s.size()) return "";
return s.substr(start, len);
}
bool check(int* cnt, int* cnt_t)
{
for(int i = 0; i < 128; i++)
if(cnt[i] < cnt_t[i])
return false;
return true;
}
};上述代码已经可以AC了,但是每次检查是否满足性质时,都要循环128次,能否优化?
我们可以用 l e s s less less 维护当前子串有 l e s s less less 种字母的出现次数小于 t t t 中对应字母的出现次数。若 l e s s = = 0 less==0 less==0 则说明该子串满足性质。
cpp
class Solution {
public:
string minWindow(string s, string t) {
int cnt_t[128]{}, cnt[128]{};
for(auto e : t) cnt_t[e]++;
int start = -1, len = s.size() + 1;
int less = 0; // 记录有less种字母的出现次数小于t中对应字母的出现次数
for(int i = 0; i < 128; i++)
if(cnt_t[i] > 0)
less++;
for(int l = 0, r = 0; r < s.size(); r++)
{
cnt[s[r]]++;
if(cnt[s[r]] == cnt_t[s[r]]) // 刚好相等,说明s[r]满足要求了
less--;
while(less == 0)
{
if(r - l + 1 < len)
{
len = r - l + 1;
start = l;
}
// 出窗口时,原本相等,s[l]出去后,说明该字符不满足要求了
if(cnt[s[l]] == cnt_t[s[l]])
less++;
cnt[s[l]]--;
l++;
}
}
if(len > s.size()) return "";
return s.substr(start, len);
}
};专题三:求子数组个数
(1)越短越合法
例3.1.1 乘积小于 K 的子数组
题目链接:713. 乘积小于 K 的子数组

子数组性质:所有元素的乘积 < k < k <k。
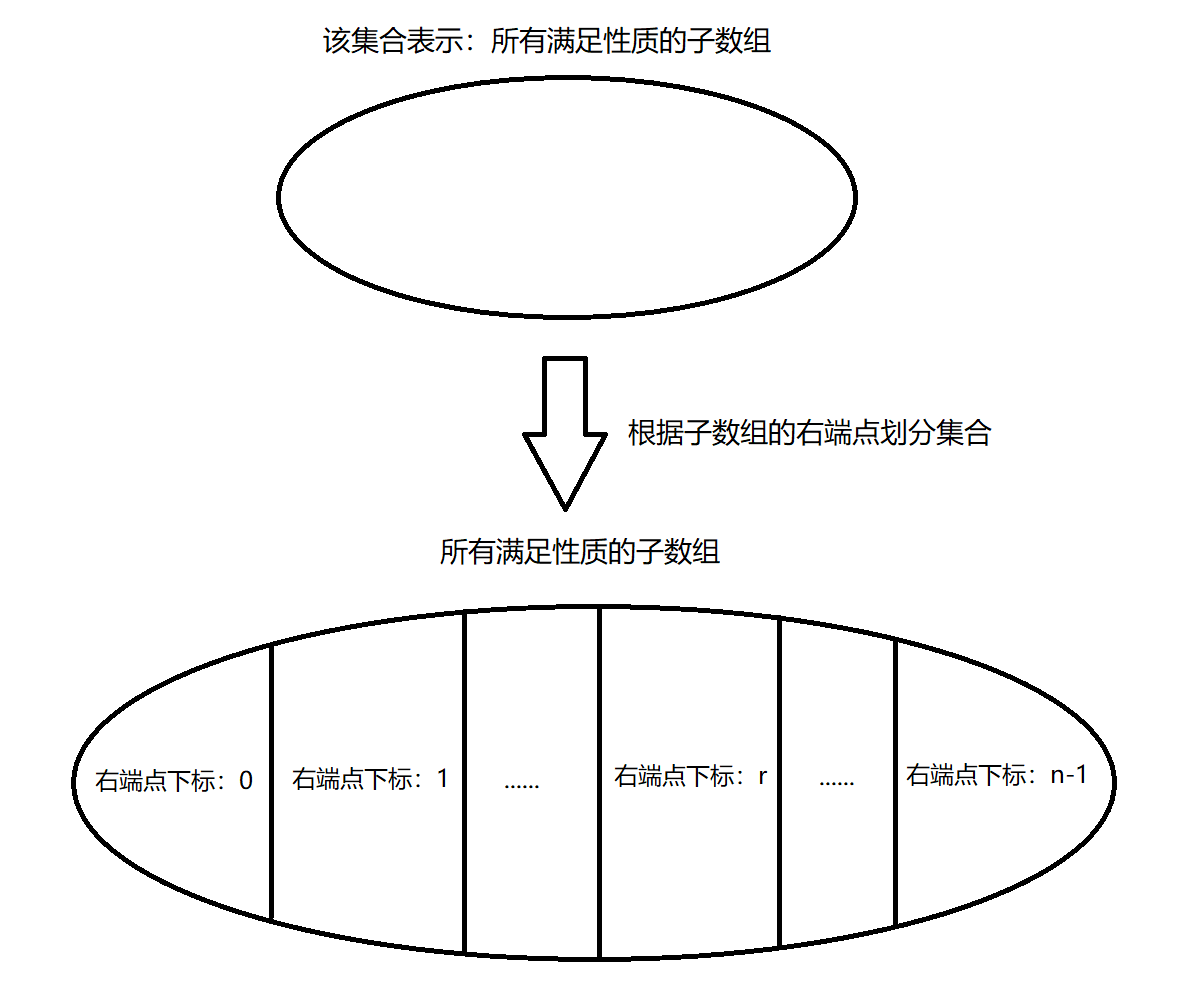
令 n u m s nums nums 的元素个数为 n n n,从集合角度看待问题:
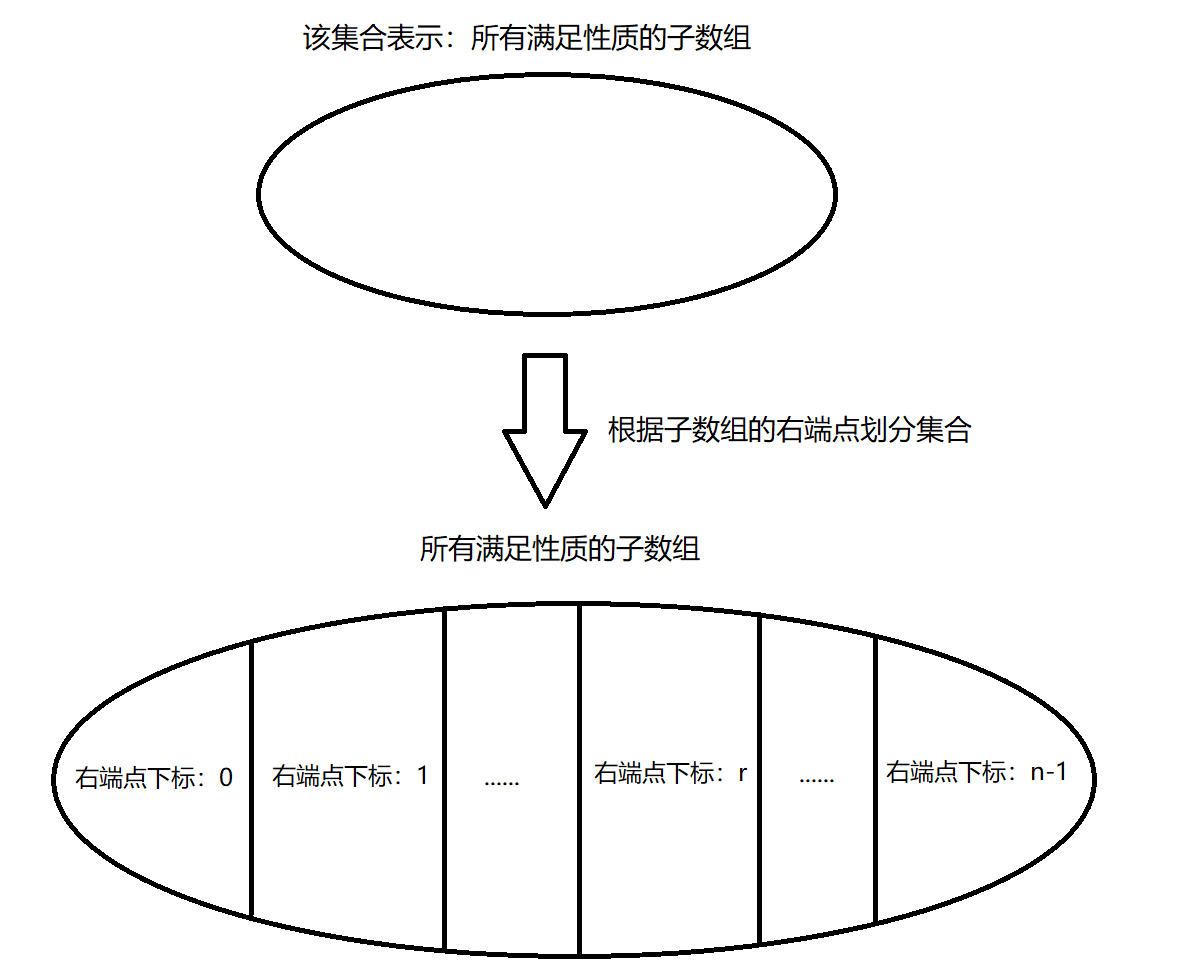
以 示例一 的输入数据为例:
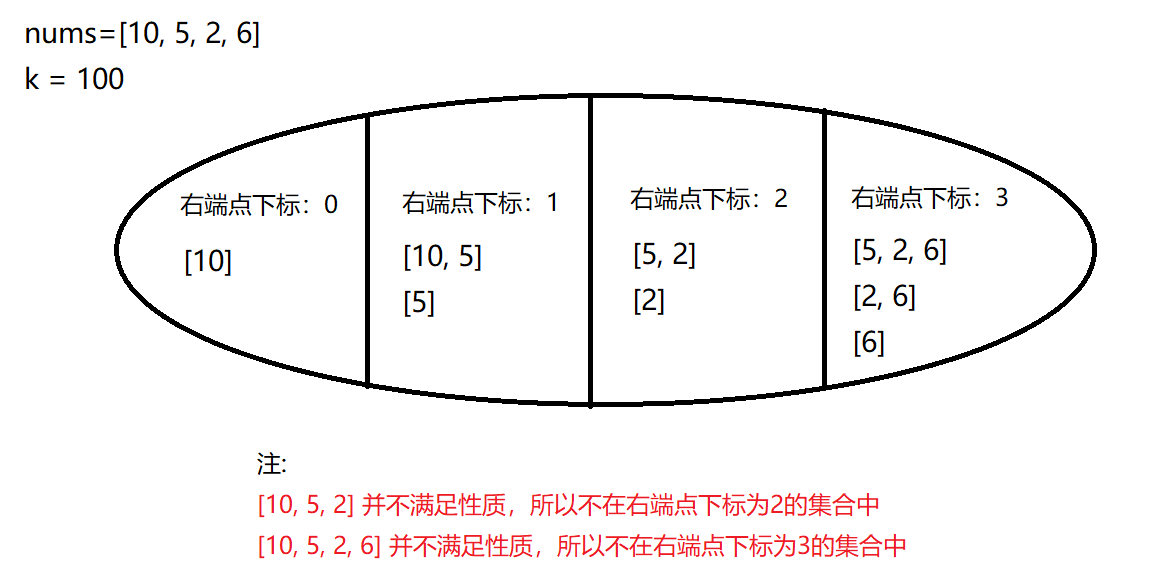
把所有划分的子集的元素个数累加起来就是最终答案。
对于 右端点下标为 r r r 的子集,如何求其包含的子数组个数?
答:
- 由于 n u m s nums nums 的元素都为正数,如果 [ l , r ] [l, r] [l,r] 区间的子数组满足性质,那么必然有 [ l + d , r ] [l+d, r] [l+d,r] 也满足性质,其中 d ≥ 0 d \ge 0 d≥0 且 l + d ≤ r l+d \le r l+d≤r。(越短越合法)
- 因此我们只需求出以 r r r 为右端点的最长满足性质 的子数组 [ l , r ] [l, r] [l,r] 即可,这样的话该子集包含的子数组有: [ l , r ] 、 [ l + 1 , r ] 、 [ l + 2 , r ] 、 . . . 、 [ r , r ] [l,r]、[l+1,r]、[l+2,r]、...、[r,r] [l,r]、[l+1,r]、[l+2,r]、...、[r,r],个数为 r − l + 1 r-l+1 r−l+1 。
- 求最长满足性质的子数组直接用专题一的模板即可。
cpp
class Solution {
public:
int numSubarrayProductLessThanK(vector<int>& nums, int k) {
int res = 0, mul = 1;
// res用于统计答案;mul 维护当前子数组的所有元素的乘积
for(int l = 0, r = 0; r < nums.size(); r++)
{
mul *= nums[r];
while(l <= r && mul >= k) // 这里需加上l <= r。不加的话,k=0时就会出错
{
mul /= nums[l];
l++;
}
res += r - l + 1; // 统计以r为右端点的所有满足性质的子数组
}
return res;
}
};解题套路
这种类型的题目就是让求满足某种性质 的子数组的个数,且该性质具备以下特点:
对于区间 [ l , r ] [l,r] [l,r] 与 [ L , R ] [L,R] [L,R], L ≤ l L \le l L≤l, R ≥ r R \ge r R≥r,则有:
- 若 [ L , R ] [L, R] [L,R] 区间的子数组满足性质 ,那么 [ l , r ] [l, r] [l,r] 区间的子数组也满足性质 。(越短越合法)
其实就是特点1 的逆否命题 。(换句话说,越短越合法 与 特点1 等价)
求解通法 :用专题一的模板求出以 r r r 为右端点的最长 满足性质的子数组 [ l , r ] [l,r] [l,r],累加 r − l + 1 r-l+1 r−l+1 。
例3.1.2 美观的花束
题目链接:LCP 68. 美观的花束

子数组性质:每种花的数量 ≤ c n t \le cnt ≤cnt 。
你可以按照上一题的分析步骤来做此题,这里直接简要概述。
用专题一的模板求出以 r r r 为右端点的最长满足性质的子数组 [ l , r ] [l,r] [l,r],然后累加 r − l + 1 r-l+1 r−l+1 。
cpp
class Solution {
public:
int beautifulBouquet(vector<int>& flowers, int cnt) {
int res = 0;
unordered_map<int, int> h; // {种类,数量}
// 判断是否满足性质
auto check = [&]()
{
for(auto& e : h)
if(e.second > cnt)
return false;
return true;
};
for(int l = 0, r = 0; r < flowers.size(); r++)
{
h[flowers[r]]++; // 右端进窗口
while(!check()) // 判断是否不满足性质
{
h[flowers[l]]--;
l++;
}
res += r - l + 1;
}
return res;
}
};考虑优化 w h i l e while while 的判断条件,对于 [ l , r ] [l, r] [l,r] 区间,由于上一次维护的 [ l , r − 1 ] [l,r-1] [l,r−1] 是最长满足性质的,那么若 [ l , r ] [l, r] [l,r] 不满足性质,那必定是右端点破坏了该性质,因此只需判断右端点即可。
cpp
class Solution {
public:
int beautifulBouquet(vector<int>& flowers, int cnt) {
int res = 0;
unordered_map<int, int> h; // {种类,数量}
for(int l = 0, r = 0; r < flowers.size(); r++)
{
h[flowers[r]]++;
while(h[flowers[r]] > cnt) // 只需判断右端点即可
{
h[flowers[l]]--;
l++;
}
res += r - l + 1;
}
return res;
}
};(2)越长越合法
例3.2.1 统计最大元素出现至少 K 次的子数组

令 m a x V a l maxVal maxVal 为 n u m s nums nums 的最大元素,子数组性质:值为 m a x V a l maxVal maxVal 元素个数 ≥ k \ge k ≥k 。
令 n u m s nums nums 的元素个数为 n n n,从集合角度看待问题:
以 示例一 为例:
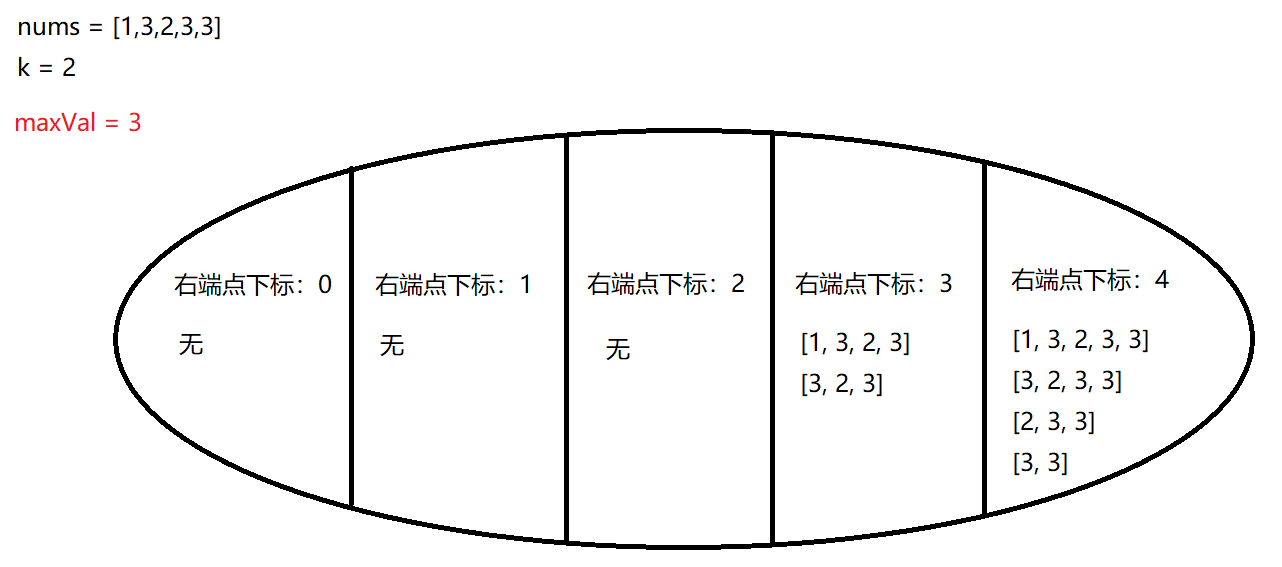
对于 右端点下标为 r r r 的子集,如何求其包含的子数组个数?
答:
- 注意到该性质越长越合法 :如果 [ l , r ] [l, r] [l,r] 区间的子数组满足性质,那么必然有 [ l − d , r ] [l-d, r] [l−d,r] 也满足性质,其中 d ≥ 0 d \ge 0 d≥0 且 l − d ≥ 0 l-d \ge 0 l−d≥0。
- 因此我们只需求出以 r r r 为右端点的最短满足性质 的子数组 [ l , r ] [l, r] [l,r] 即可,这样的话该子集包含的子数组有: [ 0 , r ] 、 [ 1 , r ] 、 [ 2 , r ] 、 . . . 、 [ l , r ] [0,r]、[1,r]、[2,r]、...、[l,r] [0,r]、[1,r]、[2,r]、...、[l,r],个数为 l + 1 l+1 l+1 。
- 求最短满足性质的子数组直接用专题二的模板即可。
cpp
class Solution {
public:
long long countSubarrays(vector<int>& nums, int k) {
int maxVal = 0;
for(auto e : nums) maxVal = max(maxVal, e);
long long res = 0;
int cnt = 0; // 用于记录子数组中值为maxVal的元素个数
for(int l = 0, r = 0; r < nums.size(); r++)
{
if(nums[r] == maxVal) cnt++;
while(cnt >= k)
{
if(nums[l] == maxVal) cnt--;
l++;
}
// 到这里[l, r]是不满足性质的,[l-1, r]才是以r为右端点的最短满足性质的子数组
// 那么[0, r], [1, r], ... [l-1, r]都满足性质,个数为l
res += l;
}
return res;
}
};解题套路
这种类型的题目就是让求满足某种性质 的子数组的个数,且该性质具备以下特点:
对于区间 [ l , r ] [l,r] [l,r] 与 [ L , R ] [L,R] [L,R], L ≤ l L \le l L≤l, R ≥ r R \ge r R≥r,则有:
- 若 [ l , r ] [l, r] [l,r] 区间的子数组满足性质 ,那么 [ L , R ] [L, R] [L,R] 区间的子数组也满足性质 。(越长越合法)
其实就是特点2 的逆否命题 。(换句话说,越长越合法 与 特点2 等价)
求解通法 :用专题二的模板求出以 r r r 为右端点的最短 满足性质的子数组 [ l − 1 , r ] [l-1,r] [l−1,r],累加 l l l 。
(3)恰好型滑动窗口
例3.3.1 K 个不同整数的子数组
题目链接:992. K 个不同整数的子数组

子数组性质:不同元素的个数 = k =k =k 。
这类题目第一次接触不太好想到如何去做,具体实现:
- 计算有多少个不同元素的个数 ≥ k ≥k ≥k 的子数组。
- 计算有多少个不同元素的个数 > k >k >k 的子数组。 > k >k >k 可以转为 ≥ k + 1 ≥k+1 ≥k+1
答案就是不同元素的个数 ≥ k ≥k ≥k 的子数组个数,减去不同元素的个数 ≥ k + 1 ≥k+1 ≥k+1 的子数组个数。
计算那两类子数组的个数的解法类似专题三前两部分内容。
注:也可以用 ≤ k ≤k ≤k 减去 ≤ k − 1 ≤k−1 ≤k−1
解法一( ≥ k \ge k ≥k 减去 ≥ k + 1 \ge k+1 ≥k+1):
cpp
class Solution {
public:
int subarraysWithKDistinct(vector<int>& nums, int k) {
// 计算子数组个数,子数组性质:不同元素的个数 >= k
// 该性质越长越合法,思路类似专题三的(2)
auto solve = [&](int k)
{
unordered_map<int, int> h; // {元素,该元素的个数}
int res = 0;
for(int l = 0, r = 0; r < nums.size(); r++)
{
h[nums[r]]++;
while(h.size() >= k)
{
if(--h[nums[l]] == 0)
h.erase(nums[l]);
l++;
}
// [0, r], [1, r], ..., [l-1, r]都满足
res += l;
}
return res;
};
return solve(k) - solve(k + 1);
}
};解法二( ≤ k \le k ≤k 减去 ≤ k − 1 \le k-1 ≤k−1):
cpp
class Solution {
public:
int subarraysWithKDistinct(vector<int>& nums, int k) {
// 计算子数组个数,子数组性质:不同元素的个数 <= k
// 该性质越短越合法
auto solve = [&](int k)
{
unordered_map<int, int> h; // {元素,该元素的个数}
int res = 0;
for(int l = 0, r = 0; r < nums.size(); r++)
{
h[nums[r]]++;
while(h.size() > k)
{
if(--h[nums[l]] == 0)
h.erase(nums[l]);
l++;
}
// [l, r], [l+1, r], ..., [r, r]都满足
res += r - l + 1;
}
return res;
};
return solve(k) - solve(k - 1);
}
};相关练习题
参考灵神第二个不定长滑动窗口题单:
分享丨【算法题单】滑动窗口与双指针
结语
滑动窗口可以求解满足某种性质的最长子数组、最短子数组、子数组个数,而且该性质具备 " " "单调性 " " " ,我们可以在暴力做法上进行优化。(这里的单调性是指 越长越合法 / 越短越合法)
滑动窗口也可以称为同向双指针。