编译后视角的运算(关于中，后缀（逆波兰）表达式的计算)

前言：

本文讲解中缀表达式，以及后缀表达式及其求值。以及这种方法跟编译后的汇编语言中的关系。带你了解为什么要有中后缀表达式。

一.中后缀表达式的认识

1.1 中缀表达式

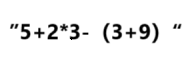
上图这是我们人自己写的一个表达式，一个正常顺序的运算式，它就是中缀表达式，中缀中缀，符号在数字中缀进去。

对人来说可以人工感觉判断优先级，比如先计算2*3和先计算3+9，但是计算机不能啊，我们的计算机最底层是指令级别的往上走一层就是汇编了，作为助记符它依然是指令级别的语言，所以编译后依然是 add，sub， mult，div （加减乘除）这样都是一个个的指令，都是二元运算的作用于寄存器上的，所以计算机要计算就要把中缀表达式转为为一个个的两个两个的计算。

1.2 后缀表达式

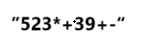
后缀表达式，这不就来了吗，如上图，这家伙。显然后缀后缀，就是说符号在数字后面缀入，就是后缀咯！ 拓展一下后缀表达式也叫做逆波兰表达式没什么稀奇的（Reverse Polish Notation，RPN）。

还记得我们上面说中缀的时候吗？ 我们说（计算机）汇编中运算能识别的就是一个个指令：add，sub， mult，div， 这些个家伙都是针对二元的。 后缀的运算其实也很简单就是：直接计算的想法是： 看到从左往右遍历，遇到数字入栈，遇到符号出栈两个用这个符号计算他们俩： 现在很快的每次都是二元的运算了。

二. 中缀转后缀：后缀转中缀

2.1 中缀转后缀

中缀转后缀，简单来说就是1.一个个的结合起来，遇到符号优先级不同考虑是否优先计算，遇到括号先计算括号。

直接理解中缀转后缀（符号会跟最近左边两个元素在一起计算）： 如上图：

从左向右顺序遍历中缀字符串则： 23* 先计算 然后在+号计算5跟23乘积之后的值，

那么就是：523*+ （初步转换为这样 遇到第一个符号计算的是 23* 得到的值计算 +后左边两个值就是 5+23*）

既然理解了自然的就是： 523*+39+- 发现了吗 先计算了+对应的39然后计算了 左边和右边的值。这就是中缀转后缀。

算法实现思路 ： 1.数据结构： 准备一个符号栈 stack<char> st， 和一个结构列表（数组） 用vector<string> sum；

解释一下为什么用string作为结果列表 而不是char vector<char> 确实可以放字符如 "1+2+3"这样的单个字符，但是如果数字是:-1 以及 19 这样的复合字符 还是作为字符串"-19"会更为合适。

2. 算法设计： 设计一个函数: InfixtoPostfix（vector<string>infix）

遍历中缀infix： 分情况考虑对应的值。 具体参考如下：

参考代码如图：

// 中缀表达式转后缀表达式    

bool smaller(string cur, string top)
{
    int curpro = 0;
    int toppro = 0;
    if (cur == "+" || cur == "-")
    {
        curpro = 1;
       }
    else if (cur == "*" || cur == "/")
    {
        curpro = 2;
    }

    if (top == "+" || top == "-")
    {
        toppro = 1;
    }
    else if (top == "*" || top == "/")
    {
        toppro = 2;
    }

    return curpro < toppro;

}
// "-23"
// "-" "23" "*""4"  "23""4""*""-"
vector<string> InfixToPostfix(vector<string>ex)
{
    vector<string> sum;// 结果字符串
    stack<string> st;  // 符号栈
    for (int i = 0;i < ex.size();i++)
    {
            

       
        if(ex[i]=="(" || ex[i] == ")") {

            if (ex[i] == "(")
            {
                st.push("(");
              }
            else {
                while (st.top() != "(") // 弹出 直到遇到左括号
                {
                    sum.push_back(st.top());
                    st.pop();
                }
                st.pop();
            }
        }
        else if (ex[i] == "+" || ex[i] == "-" || ex[i] == "*" || ex[i] == "/")
        {
            if (st.empty())
            {
                st.push(ex[i]);
            }
            else if (smaller(ex[i], st.top()))
            {
                // 如果当前遍历元素确实小于栈顶的优先级 就开始弹出咯 直到空
                while (!st.empty()) // 弹出 直到遇到左括号
                {
                    sum.push_back(st.top());
                    st.pop();
                }
                st.push(ex[i]);

               
            }
            else {
                st.push(ex[i]);
            }
        }
        else 
        {
            sum.push_back(ex[i]);
        }
    }
    while (!st.empty())
    {
        sum.push_back(st.top());
        st.pop();
    }

    return sum;

}

这里的实现，对于优先级的考量，我专门写了一个函数，不同的类型我标定了一个优先级数，+-是1，默认的是0，*/是2.

算法思路可以看前面的图片。

2.2 后缀表达式求值

现在我们有了后缀表达式，那我们如何求值呢，后缀表达式更像一种提前把优先级决定好了，最靠近符号的左侧两个数便是进行符号运算的操作数。这样的意义其实是为了模仿我们的转汇编后的指令编写的过程，因为计算机指令不是多个数同时运算同时兼顾优先级，这是需要我们进行转汇编过程的时候就已经写好了。

这也就意味着我们的源代码对于涉及到运算的时候，编译转汇编的时候就已经将中缀写成了后缀表达式了。

这里就将中缀表达式已经转后缀了，下面进行的是后缀表达式求值的过程了。

1+2*（3-4）

这里的后缀表达式应该是： 1234-*+

后缀求值的思想

遍历后缀表达式遇到一个符号就把邻近（靠左）的两个表达式进行计算，然后放回去，在遍历遇到符号又把邻近的进行计算。
算法思路： 这里需要借助一个辅助栈 stack<int>来实现，遍历后缀表达式： 遇到数字直接入栈，遇到符号则开始出栈计算，然后把计算结果放回去，直到遍历完全部，栈顶也就是最终剩余一个元素，这就是计算结果。

int str_evaluate(int& eax, int& ebx, string& sy)
{
    if (sy == "+")
    {
        return eax + ebx;
    }
    else if (sy == "-")
    {
        return eax - ebx;
    }
    else if (sy == "*")
    {
        return eax * ebx;
    }
    else if (sy == "/")
    {
        return eax / ebx;
    }
    return 0;
}


int evalRPN(vector<string>& px) {
    int eax = 0;
    int ebx = 0;
    stack<int> st;// 中间栈 
    for (int i = 0;i < px.size();i++)
    {
        if (px[i] == "+" || px[i] == "-" || px[i] == "*" || px[i] == "/") {

            int ebx = st.top();
            st.pop();
            int eax = st.top();
            st.pop();
            // 符号求值 
            int sum = str_evaluate(eax, ebx, px[i]);
            st.push(sum);
        }
        else {
            st.push(stoi(px[i]));  //数字进
        }
    }
    return st.top();

}

strtoi

这会将传入的字符串转换为整形。具体的翻译自己参考啦，自己翻的才是最好的！

2.3 后缀转中缀

其实你要是会后缀表达式求值，那你一定会后缀转中缀，简单来说就是不停的加括号咯，这里的作用其实不大，一方面我觉得是思维考量，其次就是有些无趣的笔试题，还有场景就是： 如果传递的是后缀希望被翻译为中缀。

思路：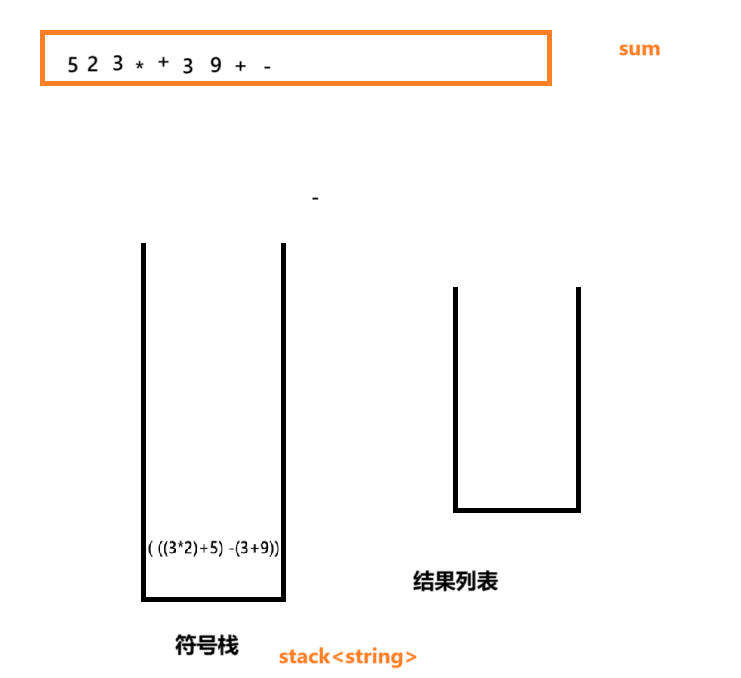

可以准备一个栈 stack<string>就行了 ，这个栈作为结果列表，开始遍历表达式吧： 遇到数字直接放入列表中，遇到符号就开始把弹出栈中两个元素，然后开始修改字符串操作，得到一个这两个元素的运算后的结果加上括号。再把这个字符串放回去：

简单来说就是： 523 遇到*

拿出来 ： "（2*3）" 放回去变成 "5""(2*3)" 又遇到了+

又变为： "（5+(2*3)）" 就这样继续遍历直到只剩余一个字符串咯！

具体的代码思路我解释啦，具体的代码就大家自己写咯！

三. 挑战一个小项目---- 实现控制台字符串计算机

需求如图：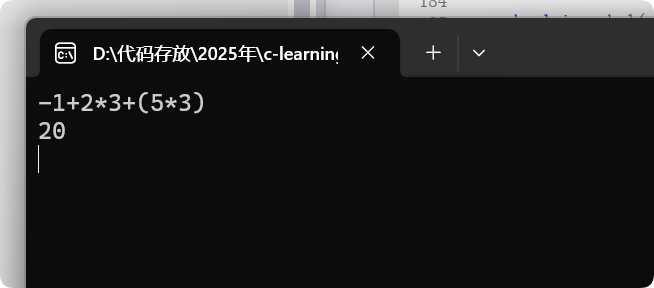

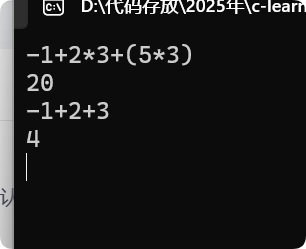
就是说我在控制台输入字符串，然后输出一个计算结果，这个过程涉及到的计算要求用后缀表达式求值来提高效率！

需求描述：

我们这里涉及到用户输入都是中缀表达式，我们现有函数：中缀转后缀传入的参数就是后缀表达式：vector<string>infix ,但是对于用户输入的肯定是字符串所以我们这里肯定要设计一个字符串拆分。

其次，拆分之后就轻松了，我们只需要调用中缀转后缀函数，以及后缀表达式求值函数即可，最终输出表达式的值！

3.1 项目流程图

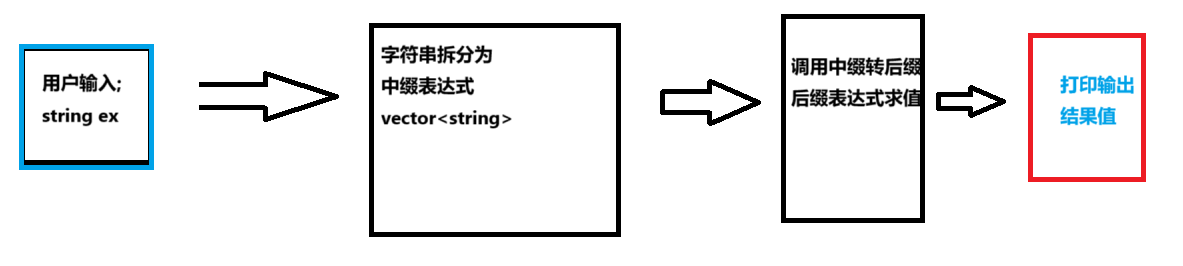
主函数输入：

int main() {

    string input;
    vector<string>infix;

    while (std::getline(cin,input))
    {
        vector<string>infix;
        stoken_input(input, infix);
        // 先转后缀 
        vector<string> postfix=  InfixToPostfix(infix);
        cout<<evalRPN(postfix)<<endl;
     }


    return 0;
}

3.2 字符串拆分

这里用getline，是为了一次性把用户的输入全部放到字符串string input中，其次是字符串拆分：

思路就是： 遍历字符串，我们分为四类： 数字，空格，符号，带负数的数字，

这里拆分的情况，有一定难度的就是对于这个负数的拆分，所以我我们研究用户输入，观察-号的出现一般是第一个位置 也就是 -1+2+(-10) 因为之后的位置的-号要么加上（）才能被认为是一个数，要么是1-2 这里还不如看成一个运算了。

之后的思路就是调用函数打印了。

我们这里把对于符号的判断封装了一个函数。

bool issymbol(char& input)
{
     return input == '+' || input == '-' || input == '*' || input == '/' ||input==' '||input=='(' || input == ')';
}



void stoken_input(string &input,vector<string>&infix) {

    int i = 0;
    // 特殊情况 第一个数字就是- 负数
    
      while (i < input.size())
    {
           
        if (issymbol(input[i]))
        {
               // 负数
            if (input[i] == '-' && (i == 0 || input[i - 1] == '('))
            {
                string st;
                st += '-';
                i++;

                // 数字进入
                while (!issymbol(input[i]))
                {

                    st += input[i++];
                }
                infix.push_back(st);
            }
                  // 这里是除了空格外的符号我们进行插入
             else if (input[i] != ' ') {
                string st;
                st += input[i];
                infix.push_back(st);// char*对应的单个字符 调用string的拷贝构造 进行赋值 
                i++;
            }
//             这是遇到空格了 直接跳过
            else {
                i++;
            }
           
          }
//             除了上面的情况我们认为这是数字
        else {
            string st;
            while (i<input.size() && !issymbol(input[i]))
            {
                st += input[i++];
            }
            infix.push_back(st);
             
        }

      }
}  

3.3 项目代码--- 可直接copy运行

bool smaller(string cur, string top)
{
    int curpro = 0;
    int toppro = 0;
    if (cur == "+" || cur == "-")
    {
        curpro = 1;
       }
    else if (cur == "*" || cur == "/")
    {
        curpro = 2;
    }

    if (top == "+" || top == "-")
    {
        toppro = 1;
    }
    else if (top == "*" || top == "/")
    {
        toppro = 2;
    }

    return curpro < toppro;

}
// "-23"
// "-" "23" "*""4"  "23""4""*""-"
vector<string> InfixToPostfix(vector<string>ex)
{
    vector<string> sum;// 结果字符串
    stack<string> st;  // 符号栈
    for (int i = 0;i < ex.size();i++)
    {
            

       
        if(ex[i]=="(" || ex[i] == ")") {

            if (ex[i] == "(")
            {
                st.push("(");
              }
            else {
                while (st.top() != "(") // 弹出 直到遇到左括号
                {
                    sum.push_back(st.top());
                    st.pop();
                }
                st.pop();
            }
        }
        else if (ex[i] == "+" || ex[i] == "-" || ex[i] == "*" || ex[i] == "/")
        {
            if (st.empty())
            {
                st.push(ex[i]);
            }
            else if (smaller(ex[i], st.top()))
            {
                // 如果当前遍历元素确实小于栈顶的优先级 就开始弹出咯 直到空
                while (!st.empty()) // 弹出 直到遇到左括号
                {
                    sum.push_back(st.top());
                    st.pop();
                }
                st.push(ex[i]);

               
            }
            else {
                st.push(ex[i]);
            }
        }
        else 
        {
            sum.push_back(ex[i]);
        }
    }
    while (!st.empty())
    {
        sum.push_back(st.top());
        st.pop();
    }

    return sum;

}

//int main() {
//
//    string infix = "1+2*3-(3+4)";
//    string postfix = InfixToPostfix(infix);
//    cout << postfix;
//
//    return 0;
//}

// 验证 编译过程中的计算 


int str_evaluate(int& eax, int& ebx, string& sy)
{
    if (sy == "+")
    {
        return eax + ebx;
    }
    else if (sy == "-")
    {
        return eax - ebx;
    }
    else if (sy == "*")
    {
        return eax * ebx;
    }
    else if (sy == "/")
    {
        return eax / ebx;
    }
    return 0;
}


int evalRPN(vector<string>& px) {
    int eax = 0;
    int ebx = 0;
    stack<int> st;// 中间栈 
    for (int i = 0;i < px.size();i++)
    {
        if (px[i] == "+" || px[i] == "-" || px[i] == "*" || px[i] == "/") {

            int ebx = st.top();
            st.pop();
            int eax = st.top();
            st.pop();
            // 符号求值 
            int sum = str_evaluate(eax, ebx, px[i]);
            st.push(sum);
        }
        else {
            st.push(stoi(px[i]));  //数字进
        }
    }
    return st.top();

}

bool issymbol(char& input)
{
     return input == '+' || input == '-' || input == '*' || input == '/' ||input==' '||input=='(' || input == ')';
}



void stoken_input(string &input,vector<string>&infix) {

    int i = 0;
    // 特殊情况 第一个数字就是- 负数
    
      while (i < input.size())
    {
           
        if (issymbol(input[i]))
        {
            if (input[i] == '-' && (i == 0 || input[i - 1] == '('))
            {
                string st;
                st += '-';
                i++;

                // 数字进入
                while (!issymbol(input[i]))
                {

                    st += input[i++];
                }
                infix.push_back(st);
            }
            else if (input[i] != ' ') {
                string st;
                st += input[i];
                infix.push_back(st);// char*对应的单个字符 调用string的拷贝构造 进行赋值 
                i++;
            }
            else {
                i++;
            }
           
          }
        else {
            string st;
            while (i<input.size() && !issymbol(input[i]))
            {
                st += input[i++];
            }

            infix.push_back(st);
             
        }

      }
}  


int main() {
   

    string input;
    vector<string>infix;

    while (std::getline(cin,input))
    {
        vector<string>infix;
        stoken_input(input, infix);
        // 先转后缀 
        vector<string> postfix=  InfixToPostfix(infix);
        cout<<evalRPN(postfix)<<endl;
     }


    return 0;
}