文章目录
- 一、概念
- 二、构造
-
- [1.1先序序列 构造BST](#1.1先序序列 构造BST)
- [1.2中序序列 转换为BST](#1.2中序序列 转换为BST)
- 1.3中序序列链表转换为BST
- 1.4BST转换为中序序列链表
- 1.7BST的序列化和反序列化
- 1.6BST的种数
- 二、BST的增删改查
- 三、BST的其他问题
一、概念
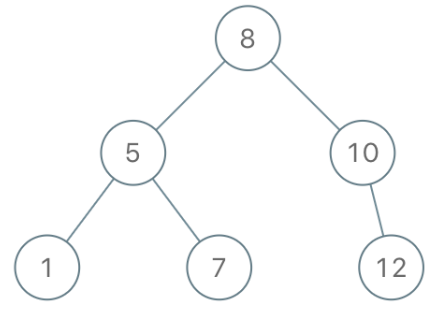
二叉搜索树(Binary Search Tree,简称 BST)是一种特殊的二叉树,其核心特性围绕 "节点值的有序性" 展开。
定义性特征:对于二叉搜索树中的任意节点,满足:
左子树所有节点的值 < 当前节点的值;
右子树所有节点的值 > 当前节点的值;左、右子树本身也必须是二叉搜索树(递归满足上述条件)。
标准 BST 中通常不允许存在值相等的节点。
衍生特征:
中序遍历结果为升序序列,得到的节点值序列是严格递增的。这是 BST 最常用的特性之一,可用于验证一棵树是否为 BST,或通过升序序列反向构造 BST。树中
最小值一定是最左侧的叶子节点(一路向左子树遍历,直到无左孩子);
树中最大值一定是最右侧的叶子节点(一路向右子树遍历,直到无右孩子)。查找目标值target的过程类似
二分查找:若当前节点值等于target,找到目标;若target小于当前节点值,递归查找左子树;若target大于当前节点值,递归查找右子树。时间复杂度为O(log n),最坏情况(退化为链表)为O(n)。
平衡二叉树是 BST 的进阶,通过额外机制保证左右子树高度差不超过 1,避免了 BST 在极端情况下退化为链表。
二、构造
1.1先序序列 构造BST
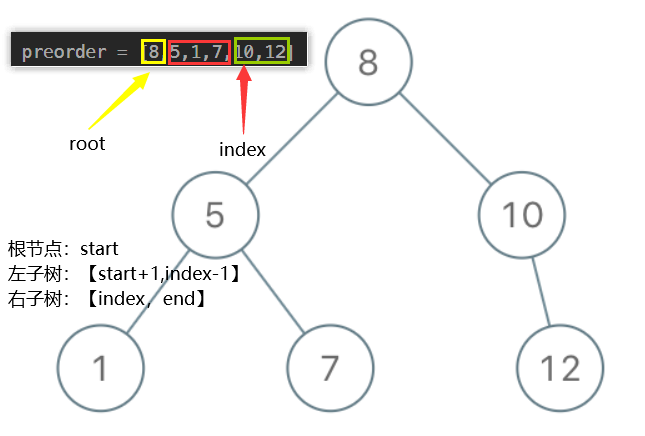
先序序列的特点是:根左右。结合BST的特性可知:
- 序列的第一个元素一定是根节点
- 根【左(比根小)】【右(比根大)】。根节点后面的元素,只要比第一个元素小的都是BST的左子树,右子树同理。
cpp
TreeNode* build(vector<int>& pre,int start,int end){
//递归的出口
if (start > end) return nullptr;
//根节点
int rootVal=pre[start];
TreeNode* root=new TreeNode(rootVal);
// 找到左子树与右子树的分割点(第一个大于根节点值的位置为右子树的第一个元素)
int index;
for(index=start+1;index<=end;index++){
if(pre[index]>rootVal) break;
}
//递归构造左子树和右子树
root->left = build(pre, start + 1, index - 1);
root->right = build(pre, index, end);
return root;
}1.2中序序列 转换为BST
与先序序列转换一样。中序序列的特点是:左根右。结合BST的性质。
- 序列的中间元素为树的根节点。
- 【左】根【右】。在根节点左边的为左子树,根节点右边的为右子树(递归构造)
cpp
TreeNode* build(vector<int>& nums,int start,int end){
if(start>end) return nullptr;
int mid=(start+end)/2;
int rootVal=nums[mid];
TreeNode* root=new TreeNode(rootVal);
root->left=build(nums,start,mid-1);
root->right=build(nums,mid+1,end);
return root;
}1.3中序序列链表转换为BST
有序链表转换成二叉搜索树的原理同 中序遍历转换为二叉树。
cpp
TreeNode* build(ListNode* head,int left,int right){
if(left>right) return nullptr;
int mid=(left+right)/2;
//访问链表在mid处的值 p指向的是根节点
ListNode* p=head;
for(int i=1;i<=mid;i++){
p=p->next;
}
TreeNode* root=new TreeNode(p->val);
//递归左右子树
root->left=build(head,left,mid-1);
root->right=build(head,mid+1,right);
return root;
}1.4BST转换为中序序列链表
- 将树按照中序遍历,遍历结果放在res中。为中序序列。
- 按照res构建链表。【next变成right】
cpp
void dfs(TreeNode* root, vector<int>& result){
if(root==nullptr) return ;
dfs(root->left,result);
result.push_back(root->val);
dfs(root->right,result);
}
TreeNode* increasingBST(TreeNode* root) {
vector<int> res;
dfs(root,res);
TreeNode* dummy=new TreeNode(-1);
TreeNode* p=dummy;
for(int val:res){
p->right=new TreeNode(val);
p=p->right;
}
return dummy->right;
}1.7BST的序列化和反序列化
- 序列化:BST先序遍历------遍历结果字符串
- 反序列化:遍历结果字符串------BST
cpp
// 前序遍历:根->左->右,将节点值拼接为字符串(用逗号分隔)
void preorder(TreeNode* node, string& result) {
if (node == nullptr) return;
// 拼接当前节点值
if (!result.empty()) {
result += ",";
}
result += to_string(node->val);
// 递归遍历左右子树
preorder(node->left, result);
preorder(node->right, result);
}
// 参考【先序序列构造BST】
TreeNode* buildBST(vector<int>& values, int start, int end) {}
// Encodes a tree to a single string.
string serialize(TreeNode* root) {
string result;
preorder(root, result);
return result;
}
// Decodes your encoded data to tree.
TreeNode* deserialize(string data) {
if (data.empty()) return nullptr;
// 将字符串分割为整数列表(前序遍历结果)
vector<int> values;
stringstream ss(data);
string item;
while (getline(ss, item, ',')) {
values.push_back(stoi(item));
}
// 根据前序遍历结果构建BST
return buildBST(values, 0, values.size() - 1);
}1.6BST的种数
- 对于 i 个节点,我们可以选择 j(1 ≤ j ≤ i)作为根节点
- 此时左子树有 j-1 个节点,右子树有 i-j 个节点
- 以 j 为根的二叉搜索树数量 = 左子树数量 × 右子树数量,即 dp[j-1] × dp[i-j]
- 对所有可能的根节点求和,得到 dp[i]
cpp
int numTrees(int n) {
vector<int> dp(n+1,0);
dp[0]=1;
dp[1]=1;
for(int i=2;i<=n;i++){
for(int j=1;j<=i;j++){
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}上述题目是BST有几种可能,下列代码是BST的每一种可能都列举出来。
cpp
// 生成[start, end]范围内所有可能的BST
vector<TreeNode*> generate(int start, int end) {
vector<TreeNode*> trees;
// 递归终止条件:区间为空,返回空节点
if (start > end) {
trees.push_back(nullptr);
return trees;
}
// 尝试以每个数作为根节点
for (int i = start; i <= end; ++i) {
// 生成左右子树
vector<TreeNode*> leftTrees = generate(start, i - 1);
vector<TreeNode*> rightTrees = generate(i + 1, end);
// 组合左子树和右子树,形成以i为根的树
for (TreeNode* left : leftTrees) {
for (TreeNode* right : rightTrees) {
TreeNode* root = new TreeNode(i);
root->left = left;
root->right = right;
trees.push_back(root);
}
}
}
return trees;
}
vector<TreeNode*> generateTrees(int n) {
if (n == 0) return {};
return generate(1, n);
}二、BST的增删改查
2.1验证是否为BST
验证所给的树是否为有效的二叉搜索树
二叉搜索树的中序遍历是有序的,且是升序的。【数组 or 递归 or 非递归】
- 解法1:将中序遍历的结果放在数组中。比较【当前节点】与【当前节点的前一个节点】
- 解法2:pre 记录中序遍历序列中 "当前节点的前一个节点"。比较当前节点与 pre 的值。
cpp
bool isValidBST(TreeNode* root) {
vector<int> inorder;
// 中序遍历
inorderTraversal(root, inorder);
// 检查是否严格递增
for (int i = 0; i < inorder.size()-1; i++) {
// 注意:必须严格小于,不能等于
if (inorder[i+1] <= inorder[i]) return 0;
}
return 1;
}
cpp
TreeNode* pre=nullptr;
bool isValidBST(TreeNode* root) {
if(root==nullptr) return 1;
if(isValidBST(root->left)==false) return 0; //左
if(pre!=nullptr && root->val <= pre->val){ //中
return 0;
}
pre=root;
return isValidBST(root->right); //右
}2.2查找值为val的节点
二叉树的特性就是:左小右大。因此想在二叉树中进行搜索某个值,可以进行比较。
- 如果val小于当前节点值------左子树中继续查找
- 如果val等于当前节点值------查找成功
- 如果val大于当前节点值------右子树中继续查找
cpp
TreeNode* searchBST(TreeNode* root, int val) {
if(root==nullptr) return nullptr;
if(root->val==val) return root;
else if(val<root->val) return searchBST(root->left,val);
else if(val>root->val) return searchBST(root->right,val);
return nullptr;
}2.3插入一个值为val的节点
BST的性质:递归处理左子树和右子树
cpp
TreeNode* insertIntoBST(TreeNode* root, int val) {
if (root == nullptr) return new TreeNode(val);
if (val < root->val) root->left = insertIntoBST(root->left, val);
else root->right = insertIntoBST(root->right, val);
return root;
}2.4删除一个值为val的节点
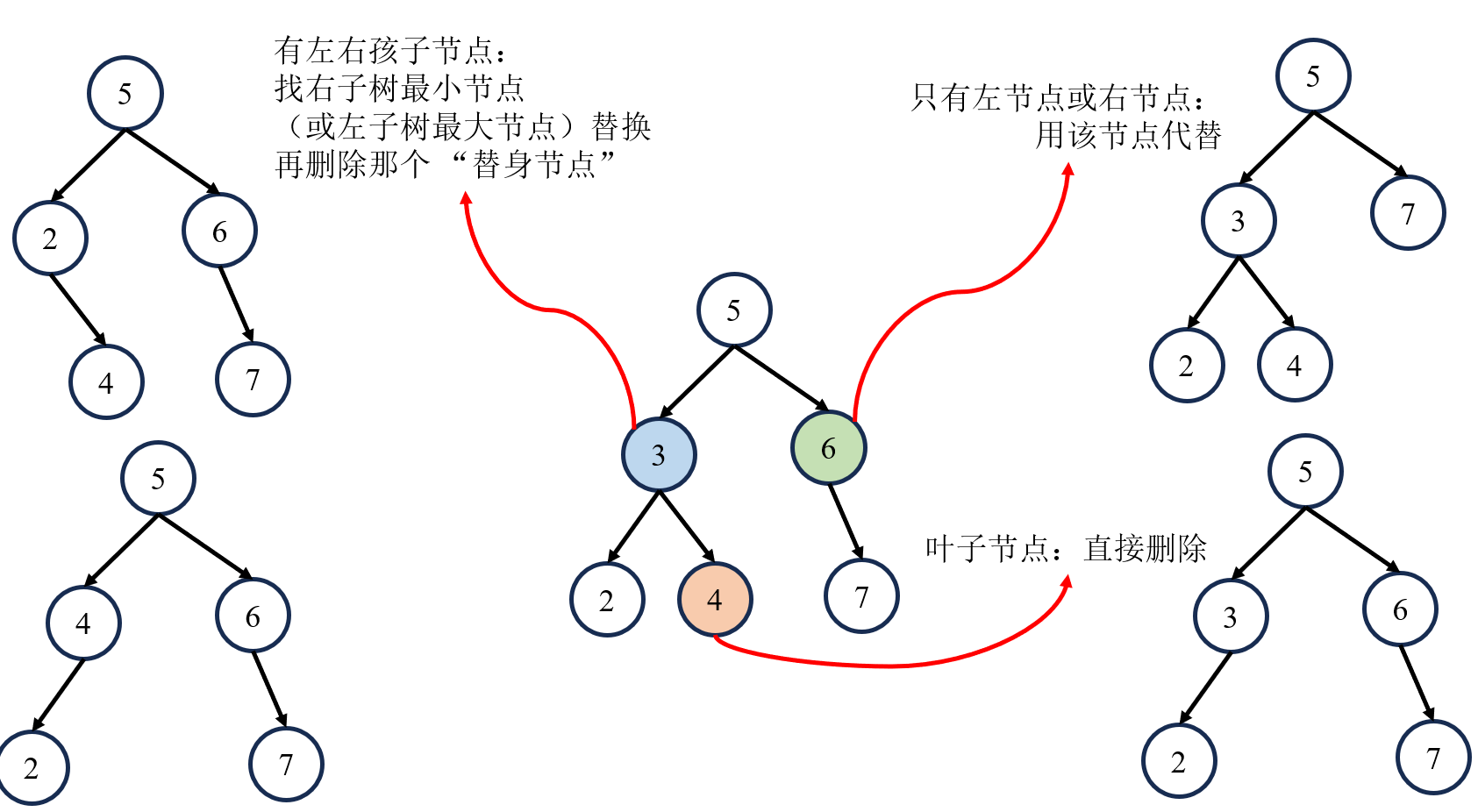
cpp
TreeNode* deleteNode(TreeNode* root, int key) {
if(root==nullptr) return nullptr;
// 查找目标节点
if(key < root->val) root->left=deleteNode(root->left,key);
else if(key > root->val) root->right=deleteNode(root->right,key);
else{
// 情况1:叶子节点,直接删除
if(root->left==nullptr && root->right==nullptr){
delete root;
return nullptr;
}
// 情况2:只有右子树(修正指针指向)
else if(root->left==nullptr){
TreeNode* temp=root->right;
delete root;
return temp;
}
// 情况3:只有左子树(修正指针指向)
else if(root->right==nullptr){
TreeNode* temp=root->left;
delete root;
return temp;
}
// 情况4:有左右子树
else{
// 找到右子树最小节点
TreeNode* minNode=root->right;
while(minNode->left!=nullptr){
minNode=minNode->left;
}
// 替换当前节点值
root->val=minNode->val;
root->right=deleteNode(root->right, minNode->val);
}
}
return root;
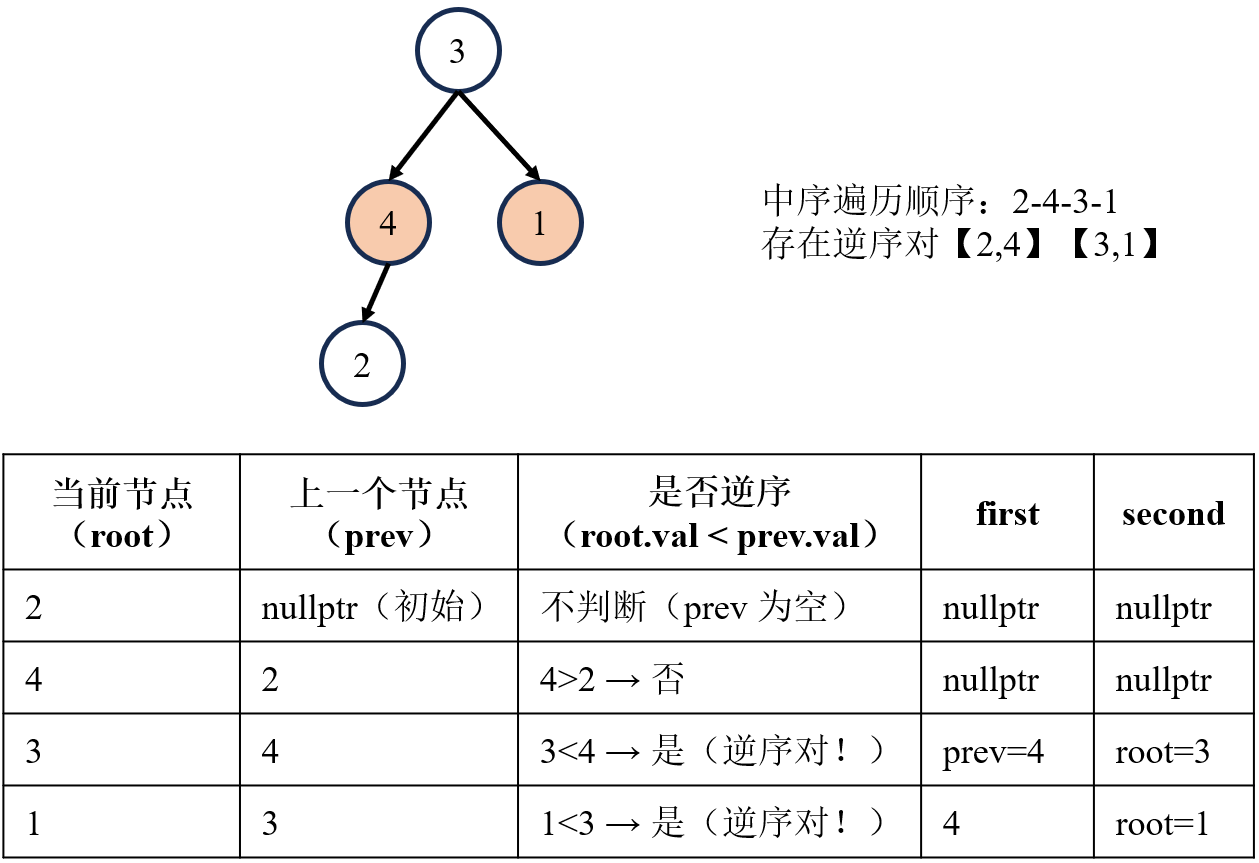
}2.5恢复错误的两节点
给你的根节点 root ,该树中的 恰好 两个节点的值被错误地交换。请在不改变其结构的情况下,恢复这棵树 。
cpp
// 中序遍历
void inorder(TreeNode* root) {
if (root == nullptr) return;
inorder(root->left); // 遍历左子树
if (prev != nullptr && root->val < prev->val) {
// 第一次发现逆序对,记录前一个节点
if (first == nullptr) first = prev;
// 第二次发现逆序对(或相邻交换的情况),记录当前节点
second = root;
}
prev = root; // 更新前一个节点
inorder(root->right); // 遍历右子树
}
void recoverTree(TreeNode* root) {
inorder(root);
swap(first->val, second->val);
}2.6修剪BST
给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变保留在树中的元素的相对结构 。
- 若当前节点值 < low:左子树所有值都 < low,直接用右子树的修剪结果替换当前节点。
- 若当前节点值 > high:右子树所有值都 > high,直接用左子树的修剪结果替换当前节点。
- 若当前节点值在范围内:保留该节点,递归修剪其左右子树并重新连接。
cpp
TreeNode* trimBST(TreeNode* root, int low, int high) {
if(root==nullptr) return nullptr;
if(root->val < low) return trimBST(root->right,low,high);
if(root->val > high) return trimBST(root->left,low,high);
root->left=trimBST(root->left,low,high);
root->right=trimBST(root->right,low,high);
return root;
}2.7平衡化
- 对原 BST 进行中序遍历,得到一个有序的节点值序列【参考树的中序遍历】
- 利用有序序列构建平衡 BST------ 通过选择序列的中间元素作为根节点,左侧元素构建左子树,右侧元素构建右子树,确保左右子树高度差不超过 1。【参考中序序列构造BST】
cpp
// 中序遍历BST,获取有序序列
void inorder(TreeNode* node, vector<int>& values) {
if (node == nullptr) return;
inorder(node->left, values);
values.push_back(node->val);
inorder(node->right, values);
}
// 从有序数组的[left, right]范围构建平衡BST
TreeNode* buildBalancedBST(vector<int>& values, int left, int right) {
if (left > right) return nullptr;
//选择中间元素作为根节点
int mid = left + (right - left) / 2;
TreeNode* node = new TreeNode(values[mid]);
// 递归构建左右子树
node->left = buildBalancedBST(values, left, mid - 1);
node->right = buildBalancedBST(values, mid + 1, right);
return node;
}
TreeNode* balanceBST(TreeNode* root) {
vector<int> values;
inorder(root, values);
return buildBalancedBST(values, 0, values.size() - 1);
}三、BST的其他问题
3.1第K小的元素
BST的中序序列是升序序列。因此中序遍历遍历整个树,同时计数,遍历到第K个的时候返回值。
cpp
int count = 0; // 记录当前遍历到第几个元素
int result = 0; // 存储第k小的元素值
// 中序遍历(左→根→右)
void inorder(TreeNode* root, int k) {
if (root == nullptr) return;
inorder(root->left, k);// 先遍历左子树
// 处理当前节点:计数+1,若达到k则记录结果
count++;
if (count == k) {
result = root->val;
return; // 找到后可提前返回,无需继续遍历
}
inorder(root->right, k);// 再遍历右子树
}
int kthSmallest(TreeNode* root, int k) {
inorder(root, k);
return result;
}3.2众数
- 方法1(对于普通的二叉树同样适用):遍历整个二叉树,在遍历过程中,用哈希表记录每个元素的个数,然后找到元素出现最多的次数记录下来,并将该元素返回给结果。
- 方法2:搜索树的中序遍历是有序序列。利用这一个性质,
cpp
class Solution {
public:
unordered_map<int,int> M;
//遍历并统计个数
void f(TreeNode* root){
if(root==nullptr) return;
M[root->val]++;
f(root->left);
f(root->right);
}
vector<int> findMode(TreeNode* root) {
vector<int> result;
int count=1;
if(root==nullptr) return result;
f(root);
//找到最大值
for(auto m:M){
if(m.second>count) count=m.second;
}
//填入result
for(auto m:M){
if(m.second==count) result.push_back(m.first);
}
return result;
}
};3.3两数之和
给定一个二叉搜索树 root 和一个目标结果 k,如果二叉搜索树中存在两个元素且它们的和等于给定的目标结果,则返回 true。
- BST按照中序遍历,将结果存储在result中。
- 利用双指针快速定位目标。
cpp
vector<int> result;
void dfs(TreeNode* root){
if(root==nullptr) return ;
dfs(root->left);
result.push_back(root->val);
dfs(root->right);
}
bool findTarget(TreeNode* root, int k) {
dfs(root);
//利用双指针,快速定位目标值
int left=0;
int right=result.size()-1;
while(left<right){
int sum=result[left]+result[right];
if(sum==k) return 1;
else if(sum<k) left++;
else right--;
}
return 0;
}3.4给定范围的节点之和
给定二叉搜索树的根结点 root,返回值位于范围 [low, high] 之间的所有结点的值的和。
依然用BST的中序遍历解决问题
cpp
int rangeSumBST(TreeNode* root, int low, int high) {
if(root==nullptr) return 0;
result.clear();
dfs(root);
int sum=0;
for(int i=0;i<result.size();i++){
if(result[i]>=low && result[i]<=high ) sum+=result[i];
}
return sum;
}3.5节点最小距离
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
转换为中序有序序列之后计算。由于中序序列是有序的,因此离得越近,差值越小。
cpp
int minDiffInBST(TreeNode* root) {
if(root==nullptr) return 0;
result.clear();
dfs(root);
int m=INT_MAX;
for(int i=0;i<result.size()-1;i++){
m=min(m,result[i+1]-result[i]);
}
return m;
}3.6二叉搜索树转换为累加树
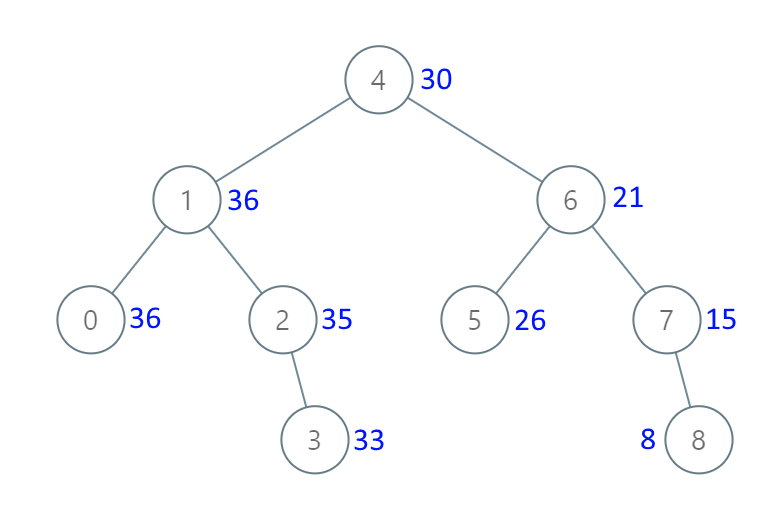
- 二叉搜索树的中序遍历是一个单调递增的有序序列。如果我们反序地中序遍历该二叉搜索树,即可得到一个单调递减的有序序列。
- 只需要反序中序遍历该二叉搜索树,记录过程中的节点值之和,并不断更新当前遍历到的节点的节点值,即可得到题目要求的累加树。
cpp
int sum=0;
TreeNode* convertBST(TreeNode* root) {
if(root==nullptr) return root;
convertBST(root->right);
sum+=root->val;
root->val=sum;
convertBST(root->left);
return root;
}3.7最近结果查询
给你一个 二叉搜索树 的根节点 root ,和一个由正整数组成、长度为 n 的数组 queries 。
请你找出一个长度为 n 的 二维 答案数组 answer ,其中 answer[i] = [mini, maxi] :
- mini 是树中小于等于 queries[i] 的 最大值 。如果不存在这样的值,则使用 -1 代替。
- maxi 是树中大于等于 queries[i] 的 最小值 。如果不存在这样的值,则使用 -1 代替。
返回数组 answer 。

- lower_bound 是 C++ 标准库 头文件中的一个二分查找函数,用于在有序序列中查找第一个大于等于目标值的元素,返回该元素的迭代器
- upper_bound:找第一个 > 目标值的元素(不包含等于的情况)。
中序遍历序列为:[1,2,3,4,6,9,10]
查询 q=5:
upper_bound找第一个 > 5 的元素是 6,前一个元素4→mini=4。
lower_bound找第一个≥5 的元素是 6→maxi=6。
结果为[4,6]。
cpp
// 中序遍历BST,生成升序序列
void inorder(TreeNode* node, vector<int>& seq) {
if (node == nullptr) return;
inorder(node->left, seq);
seq.push_back(node->val);
inorder(node->right, seq);
}
vector<vector<int>> closestNodes(TreeNode* root, vector<int>& queries) {
// 1.中序序列
vector<int> inorderSeq;
inorder(root, inorderSeq);
vector<vector<int>> answer;
for (int q : queries) {
// 2. 对每个查询,在有序序列中用二分查找找mini和maxi
int mini = -1, maxi = -1;
// 找mini:小于等于q的最大值(最后一个 <= q 的元素)
auto it_mini = upper_bound(inorderSeq.begin(), inorderSeq.end(), q);
if (it_mini != inorderSeq.begin()) {
mini = *prev(it_mini);
}
// 找maxi:大于等于q的最小值(第一个 >= q 的元素)
auto it_maxi = lower_bound(inorderSeq.begin(), inorderSeq.end(), q);
if (it_maxi != inorderSeq.end()) {
maxi = *it_maxi;
}
answer.push_back({mini, maxi});
}
return answer;
}