目录
在前面关于机器学习中的数学表示一文中提到了矩阵,实际上它是计算机领域非常重要的一种数据结构,但除了CV类(计算机视觉)开发,我们在许多软件开发场景中却很少用到它,以至于开始庆幸:
"反正在以前线性代数也没怎么学好,作用也不大嘛..."
"按说,这种观点是要受批评的。"实际上关于矩阵的计算到处都是,只是你鲜少留意罢了。或者说,当你在使用某个三方库的时候,它里面已经帮你做好高度封装,让你不再顾及里面的细节..
一、矩阵是什么
矩阵可以看做是向量的维度延伸,也就是一个二维数组。
矩阵的数学表示为\(x \in \mathbb{R}^{m*n}\),其中m和n分别代表行和列,其展开的形式如下:
\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \]
如果矩阵A = 矩阵B,那么那么 A 和 B 的行列结构,以及每个对应位置的元素都是相等的。
特殊的矩阵
- 矩阵为 1*n,只有一行,称为行向量
\[A = \begin{bmatrix} x_1 & x_2 & x_3 & \cdots & x_n \end{bmatrix} \]
- 矩阵为 n*1,只有一列,称为列向量
\[A = \begin{bmatrix} x_1 \\ x_2 \\ x_3 \\ \vdots \\ x_m \end{bmatrix} \]
- 矩阵为 n*n,行列相同,称为方阵
\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{bmatrix} \]
二、基本计算
2.1 矩阵加法
对于两个 \(m \times n\) 矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\)
\[\mathbf{A} + \mathbf{B} = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} + \begin{bmatrix} b_{11} & b_{12} & \dots & b_{1n} \\ b_{21} & b_{22} & \dots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \dots & b_{mn} \end{bmatrix} = \begin{bmatrix} a_{11}+b_{11} & a_{12}+b_{12} & \dots & a_{1n}+b_{1n} \\ a_{21}+b_{21} & a_{22}+b_{22} & \dots & a_{2n}+b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}+b_{m1} & a_{m2}+b_{m2} & \dots & a_{mn}+b_{mn} \end{bmatrix} \]
其和 \(\mathbf{C} = \mathbf{A} + \mathbf{B}\) 的元素 \(c_{ij}\) 为: $$c_{ij} = a_{ij} + b_{ij}$$
示例
给定矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\):
\[\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \]
\[\mathbf{A} + \mathbf{B} = \begin{bmatrix} 1+5 & 2+6 \\ 3+7 & 4+8 \end{bmatrix} = \begin{bmatrix} 6 & 8 \\ 10 & 12 \end{bmatrix} \]
应用场景
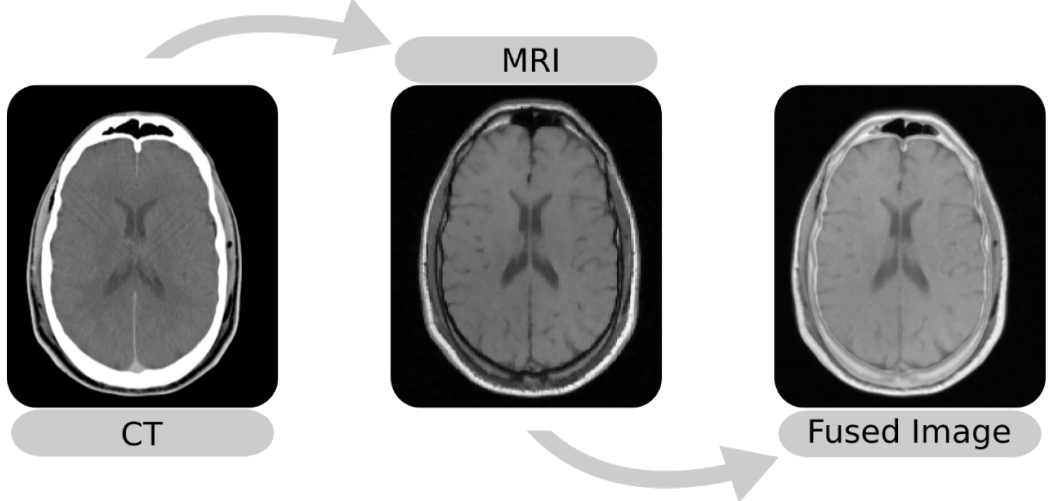
在图像处理中,图像可以表示为一个像素矩阵。将两张图像进行融合时,可以通过矩阵加法实现。
融合图像=图像A+图像B在医学影像中,CT 和 MRI 图像可以通过矩阵加法融合,帮助医生更全面地观察病灶。
2.2 矩阵减法
对于两个 \(m \times n\) 矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\)
\[\mathbf{A} - \mathbf{B} = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} - \begin{bmatrix} b_{11} & b_{12} & \dots & b_{1n} \\ b_{21} & b_{22} & \dots & b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ b_{m1} & b_{m2} & \dots & b_{mn} \end{bmatrix} = \begin{bmatrix} a_{11}-b_{11} & a_{12}-b_{12} & \dots & a_{1n}-b_{1n} \\ a_{21}-b_{21} & a_{22}-b_{22} & \dots & a_{2n}-b_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1}-b_{m1} & a_{m2}-b_{m2} & \dots & a_{mn}-b_{mn} \end{bmatrix} \]
其差 \(\mathbf{C} = \mathbf{A} - \mathbf{B}\) 的元素 \(c_{ij}\) 为:\(c_{ij} = a_{ij} - b_{ij}\)
示例
给定矩阵 \(\mathbf{A}\) 和 \(\mathbf{B}\):
\[\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad \mathbf{B} = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \]
\[\mathbf{A} - \mathbf{B} = \begin{bmatrix} 1-5 & 2-6 \\ 3-7 & 4-8 \end{bmatrix} = \begin{bmatrix} -4 & -4 \\ -4 & -4 \end{bmatrix} \]
应用场景
在安防监控中,连续帧图像之间的差异可以通过矩阵减法计算:
变化矩阵=当前帧B−前一帧A如果差异矩阵中某些区域值显著变化,说明画面中可能出现了移动物体或异常行为。

2.3 矩阵常量乘法
对于一个常数 \(k\) 和一个 \(m \times n\) 矩阵 \(\mathbf{A}\)
\[k\mathbf{A} = k \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix} = \begin{bmatrix} k a_{11} & k a_{12} & \dots & k a_{1n} \\ k a_{21} & k a_{22} & \dots & k a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ k a_{m1} & k a_{m2} & \dots & k a_{mn} \end{bmatrix} \]
其积 \(\mathbf{C} = k\mathbf{A}\) 的元素 \(c_{ij}\) 为:\(c_{ij} = k \cdot a_{ij}\)
示例
给定矩阵 \(\mathbf{A}\) 和常数 \(k=3\):
\[\mathbf{A} = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad k = 3 \]
\[3\mathbf{A} = 3 \cdot \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} = \begin{bmatrix} 3 \cdot 1 & 3 \cdot 2 \\ 3 \cdot 3 & 3 \cdot 4 \end{bmatrix} = \begin{bmatrix} 3 & 6 \\ 9 & 12 \end{bmatrix} \]
应用场景
在图像处理中,调整图像亮度可以通过对像素矩阵乘以一个常数:
亮度增强图像=k⋅原图像矩阵,这会使图像整体变亮,常用于图像增强和预处理。
 除此之外,在深度学习中,模型的权重矩阵常常需要乘以一个缩放因子(如学习率、正则化系数)来控制训练过程。
除此之外,在深度学习中,模型的权重矩阵常常需要乘以一个缩放因子(如学习率、正则化系数)来控制训练过程。
2.4 矩阵乘积
设矩阵 \(A \in \mathbb{R}^{m \times n}\),矩阵\(B \in \mathbb{R}^{n \times p}\),则它们的乘积为:\(C = AB 是一个 m \times p\) 的矩阵。
矩阵 A 和 B可相乘的条件是,A的列数与 B的行数必须相同 。乘积 C 的行数与A相同,列数与B相同。
示例
\[A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \end{bmatrix}, \quad B = \begin{bmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \\ b_{31} & b_{32} \end{bmatrix} \]
\[AB = \begin{bmatrix} a_{11}b_{11} + a_{12}b_{21} + a_{13}b_{31} & a_{11}b_{12} + a_{12}b_{22} + a_{13}b_{32} \\ a_{21}b_{11} + a_{22}b_{21} + a_{23}b_{31} & a_{21}b_{12} + a_{22}b_{22} + a_{23}b_{32} \end{bmatrix} \]
对于乘积 C来说,每个元素 \(c_{ij} 是矩阵 AA 的第 ii 行与矩阵 BB 的第 jj 列的点积:\)
\[c_{ij} = \sum_{k=1}^{n} a_{ik} \cdot b_{kj} \]
规律
-
乘法不满足交换律: 一般情况下 AB≠BA(特殊情况除外)
-
乘法满足结合律与分配律:
- A(BC)=(AB)CA(BC) = (AB)C
- A(B+C)=AB+AC
单位矩阵
单位矩阵(Identity Matrix) 是一种特殊的方阵,其主对角线上的元素全为 1,其余元素全为 0。
单位矩阵记做 I_n,对于任意矩阵 \(A \in \mathbb{R}^{n \times n}\),有:
\[AI_n=I_nA=A \]
比如,一个 3*3 的单位矩阵,计算过程如下:
\[I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]
\[AI_3 = \begin{bmatrix} 2 & -1 & 3 \\ 0 & 4 & 5 \\ -2 & 1 & 0 \end{bmatrix} \cdot \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} 2 & -1 & 3 \\ 0 & 4 & 5 \\ -2 & 1 & 0 \end{bmatrix} \]
2.5 矩阵转置
矩阵的转置是将矩阵的行列互换,记作 \(A^T\)。 如果矩阵 \(A \in \mathbb{R}^{m \times n}\),则其转置 \(A^T∈\mathbb{R}^{n×m}\)
\[A = \begin{bmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn} \end{bmatrix} \quad \Rightarrow \quad A^T = \begin{bmatrix} a_{11} & a_{21} & \cdots & a_{m1} \\ a_{12} & a_{22} & \cdots & a_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ a_{1n} & a_{2n} & \cdots & a_{mn} \end{bmatrix} \]
矩阵转置有许多计算意义,例如在图像处理中,图像可以表示为一个像素矩阵。 将图像矩阵进行转置,可以实现图像的90°旋转(配合行列反转)。
应用场景
假设你管理一家公司,销售三种产品:T恤 、裤子 和鞋子 。你有三个销售渠道:实体店A 、实体店B 和网上商店 。现在,你记录了周一和周二在每个渠道 的每种产品的具体销量。同时,这些产品的价格在不同日期可能会有微调。
我们的目标是计算出每个渠道在周一和周二分别获得了多少总收入。
1. 销量矩阵(A)
这个矩阵记录了每个渠道在周一和周二的每种产品销量。
\[\text{A} = \begin{bmatrix} 20 & 15 & 8 \\ 5 & 10 & 12 \\ 3 & 4 & 5 \end{bmatrix} \]
- 列 代表了销售渠道(从左到右依次为:实体店A,实体店B,网上商店)。
- 行 代表了产品种类。
2. 价格矩阵(B)
这个矩阵记录了三种产品在周一和周二的价格。
\[\text{B} = \begin{bmatrix} 100 & 98 \\ 200 & 195 \\ 300 & 295 \end{bmatrix} \]
- 行 代表了产品种类。
- 列 代表了日期(周一,周二)。
3. 矩阵乘法
要计算每个渠道在两天的总收入,我们将销量矩阵(A) 转置,然后与价格矩阵(B) 相乘,即 \(C=A^TB\)。
\[\text{C} = \begin{bmatrix} 20 & 5 & 3 \\ 15 & 10 & 4 \\ 8 & 12 & 5 \end{bmatrix} \times \begin{bmatrix} 100 & 98 \\ 200 & 195 \\ 300 & 295 \end{bmatrix} \]
4. 计算过程与结果
\[\text{C} = \begin{bmatrix} (20\times100+5\times200+3\times300) & (20\times98+5\times195+3\times295) \\ (15\times100+10\times200+4\times300) & (15\times98+10\times195+4\times295) \\ (8\times100+12\times200+5\times300) & (8\times98+12\times195+5\times295) \end{bmatrix} \]
5. 结果分析
\[\text{C} = \begin{bmatrix} 3900 & 3865 \\ 4700 & 4540 \\ 4700 & 4599 \end{bmatrix} \]
新的结果矩阵清晰地显示了每个渠道在每一天的总收入:
- 第一行 [3900, 3865] :实体店A 周一总收入为 3900,周二为 3865。
- 第二行 [4700, 4540] :实体店B 周一总收入为 4700,周二为 4540。
- 第三行 [4700, 4599] :网上商店 周一总收入为 4700,周二为 4599。
2.6 Hadamard乘积
矩阵的 Hadamard 乘积 ,也称为元素级乘积(element-wise product),是一种特殊的矩阵运算。与矩阵乘法不同,Hadamard 乘积不涉及行与列的点积,而是将两个相同结构的矩阵中对应位置的元素直接相乘,然后将结果组成一个新的矩阵。
如果两个矩阵 A 和 B 的维度都是 m×n,它们的 Hadamard 积 \(C=A⊙B\) 的每个元素 \(c_{ij}\) 满足:
\[c_{ij}=a_{ij}⋅b_{ij} \]
Hadamard 乘积常用于需要对数据进行逐元素加权或筛选的场景。
应用场景
在图像处理中,图像数据通常以矩阵形式存储,矩阵中的每个元素代表一个像素的亮度或颜色值。这时可以使用 Hadamard 乘积来实现图像遮罩效果,只保留图像中感兴趣的区域。
假设你有一张黑白照片,并想把照片中某一部分变暗或去除。你可以创建一个遮罩矩阵。
-
图像矩阵 (A): 一个表示图像像素值的矩阵,例如一个 3x3 矩阵。
\[\text{A} = \begin{bmatrix} 200 & 210 & 205 \\ 180 & 190 & 185 \\ 150 & 160 & 155 \end{bmatrix} \]
-
遮罩矩阵 (B): 一个与图像矩阵同维度的矩阵,其中你想保留的区域元素为1,想遮盖或变暗的区域元素为0或接近0的值。
\[B = \begin{bmatrix} 1 & 1 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \]
-
Hadamard 积 (C=A⊙B): 将两个矩阵逐元素相乘,结果是新的图像矩阵。
\[\text{C} = \begin{bmatrix} 200\times1 & 210\times1 & 205\times1 \\ 180\times0 & 190\times0 & 185\times0 \\ 150\times0 & 160\times0 & 155\times0 \end{bmatrix} \]
\[\text{C} = \begin{bmatrix} 200 & 210 & 205 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \]
最终结果是只保留了图像上半部分的像素,下半部分像素值变为0(全黑),这样便可以实现了图像的局部处理功能。
三、小试牛刀
下面使用 numpy 来实现本文提到的这些矩阵运算,包括:加法、减法、常量乘法、矩阵乘积、单位矩阵初始化,以及 Hadamard(元素乘)乘积。
代码示例
import numpy as np
# 初始化两个矩阵 A 和 B(3x3)
A = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]])
B = np.array([[9, 8, 7],
[6, 5, 4],
[3, 2, 1]])
# 1️⃣ 矩阵加法
add_result = A + B
# 2️⃣ 矩阵减法
sub_result = A - B
# 3️⃣ 常量乘法(例如 k = 2)
k = 2
scalar_mul_result = k * A
# 4️⃣ 矩阵乘积(矩阵乘法)
dot_result = np.dot(A, B)
# 5️⃣ 单位矩阵初始化(3x3)
identity_matrix = np.eye(3)
# 6️⃣ Hadamard 乘积(元素乘法)
hadamard_result = A * B
# 输出结果
print("矩阵 A:\n", A)
print("矩阵 B:\n", B)
print("矩阵加法 A + B:\n", add_result)
print("矩阵减法 A - B:\n", sub_result)
print("常量乘法 k * A:\n", scalar_mul_result)
print("矩阵乘积 A * B:\n", dot_result)
print("单位矩阵 I:\n", identity_matrix)
print("Hadamard 乘积 A HM B:\n", hadamard_result)执行上述程序,输出结果如下:
矩阵 A:
[[1 2 3]
[4 5 6]
[7 8 9]]
矩阵 B:
[[9 8 7]
[6 5 4]
[3 2 1]]
矩阵加法 A + B:
[[10 10 10]
[10 10 10]
[10 10 10]]
矩阵减法 A - B:
[[-8 -6 -4]
[-2 0 2]
[ 4 6 8]]
常量乘法 k * A:
[[ 2 4 6]
[ 8 10 12]
[14 16 18]]
矩阵乘积 A * B:
[[ 30 24 18]
[ 84 69 54]
[138 114 90]]
单位矩阵 I:
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]]
Hadamard 乘积 A HM B:
[[ 9 16 21]
[24 25 24]
[21 16 9]]四、小结
这篇文章介绍了矩阵的一些基本特征和运算方法,算是对数学不好的小伙伴做个回忆和科普吧,矩阵在机器学习中是一个重要基础,实际上很多的算法都来源于数学应用。关于矩阵的更高阶的一些特性,后面还会继续更新。