一、概念理解
"机器学习对于高值的预测保守",这是建模里很常见的现象,尤其在生态、气候、遥感这类数据分布高度偏斜的场景。
通常可以从以下几个角度理解:
1. 数据分布与样本稀缺
**在训练集里,高值样本往往非常少,远低于中低值的占比。**机器学习模型在最小化总体误差时,会更倾向于"贴合"多数样本的中低区间,从而导致对高值的预测趋向于低估。
2. 损失函数的作用
常见的损失函数(如 MSE、MAE)本质上是对"平均误差"的优化,高值样本虽然误差可能很大,但数量太少,整体在损失中的权重有限,模型就会"牺牲"这些极端点以换取整体精度。
3. 模型的正则化与泛化倾向
像 CatBoost、XGBoost 或 Random Forest 这类集成模型,会通过叶子数、深度限制、学习率衰减等方式防止过拟合。这种"保守"的机制在高值预测上会显得更明显:因为高值点往往是噪声或异常值的来源,模型宁可收缩预测值,也不愿意强行拉到很高。
4. 特征空间覆盖不足
高值样本可能对应特殊的环境条件或特征组合,但训练数据里这类情况出现很少。模型在这类区域缺乏学习支撑,只能在已有趋势上外推,结果就是"回归到均值"式的保守预测。
常见的解决思路包括:
(1)样本再平衡(过采样高值、欠采样中低值);
(2)改变损失函数(如加权MSE、Quantile Loss、Huber Loss );
(3)特征工程增强(加入更能解释高值的变量);
(4)后处理(如残差建模、分段建模)。
二、残差建模嵌入
1. 基本思路
第一次模型(主模型)已经捕捉了数据的主要趋势,但在高值区间往往出现系统性低估。此时我们可以:
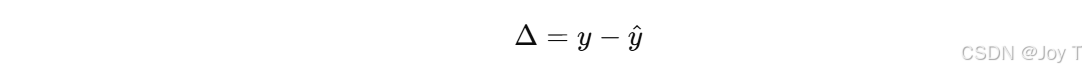
把残差 Δ当作新的目标变量,用原始特征 X 或者新构造的特征 X′ 去训练一个"残差模型"。
最终预测时,把主模型和残差模型的输出叠加:
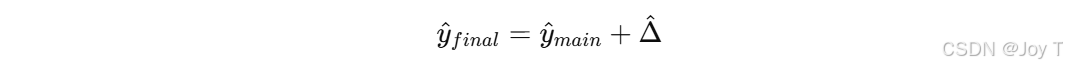
2. 为什么对高值有效
(1)残差在高值区间往往带有系统性偏差 (总是负的,表示低估),残差建模能单独学习这种规律。
(2)主模型负责整体趋势,残差模型负责修正极端值,分工明确,能提高高值段的拟合能力。
(3)相比直接让主模型去"硬拟合"高值,残差建模更稳定,因为它把任务拆解成"趋势 + 偏差"两部分。
3. 与"Δ变化"分析的关系
你提到的"对 Δ 的变化进行拟合分析"正是残差建模的核心。更进一步,可以:
(1)画残差 vs 特征的散点,看看在哪些特征区间高估/低估明显;
(2)如果残差和某些变量(比如林分密度、降雨量、温度)高度相关,就说明主模型在这类变量的高值/极端情况下表现不足;
(3)残差模型就可以重点利用这些变量来修正。【发现问题,修正问题】
4. 延伸做法
(1)Boosting 系列模型(XGBoost、CatBoost)其实就是多轮残差建模的堆叠,只不过是每棵树拟合残差的增量。
(2)在碳储量、碳通量建模里,可以尝试"主模型 + 生态学启发残差模型",例如先用 CatBoost 做趋势,再用一个小型回归模型专门拟合高值残差。
(3)如果想要"保守预测高值但同时捕捉区间",还可以考虑 分位数回归(Quantile Regression),结合残差建模一起使用。
三、损失函数更新
常见的 MSE/MAE 损失函数确实会让模型趋向于"均值回归",从而在高值区间预测偏保守。要解决这个问题,可以考虑以下几类与"极端值/不对称误差"相关的损失函数,它们能够让模型更关注高值样本:
1. 分位数损失(Quantile Loss)
机制:不是拟合均值,而是拟合某个分位数(比如 0.9 分位),这样输出会有意识地"抬高",适合不想低估高值的情况。
2. 加权损失(Weighted Loss)
机制:对高值样本加权,使其在损失函数里比低值样本更重要。
3. Huber Loss / Smooth L1 Loss
-
机制 :在误差小的时候近似 MAE,在误差大时近似 MSE,能缓解极端值对整体的冲击,但它更多是稳健化,而不是专门提高高值的预测。
-
适用场景:如果你担心高值既可能是"真值"也可能是"噪声",Huber 比较稳妥。
4. 极端值敏感损失(Tail-sensitive Loss)
-
机制 :在金融、气象等领域,有些研究会引入对尾部残差特别敏感的损失函数,比如 GEV(广义极值分布)似然、或基于 log(1+error²) 的函数。
-
作用:能让模型显式地在高值区间花更多注意力。
简单来说,如果你的目标是让模型敢于预测更高的值 :
(1)首选分位数损失(Quantile Loss) ------ 控制预测落在分布高端;
(2)其次是加权损失(Weighted MSE/MAE) ------ 强调高值样本的重要性;
(3)再配合残差建模 ------ 对高值区间的系统性低估进行二次修正。