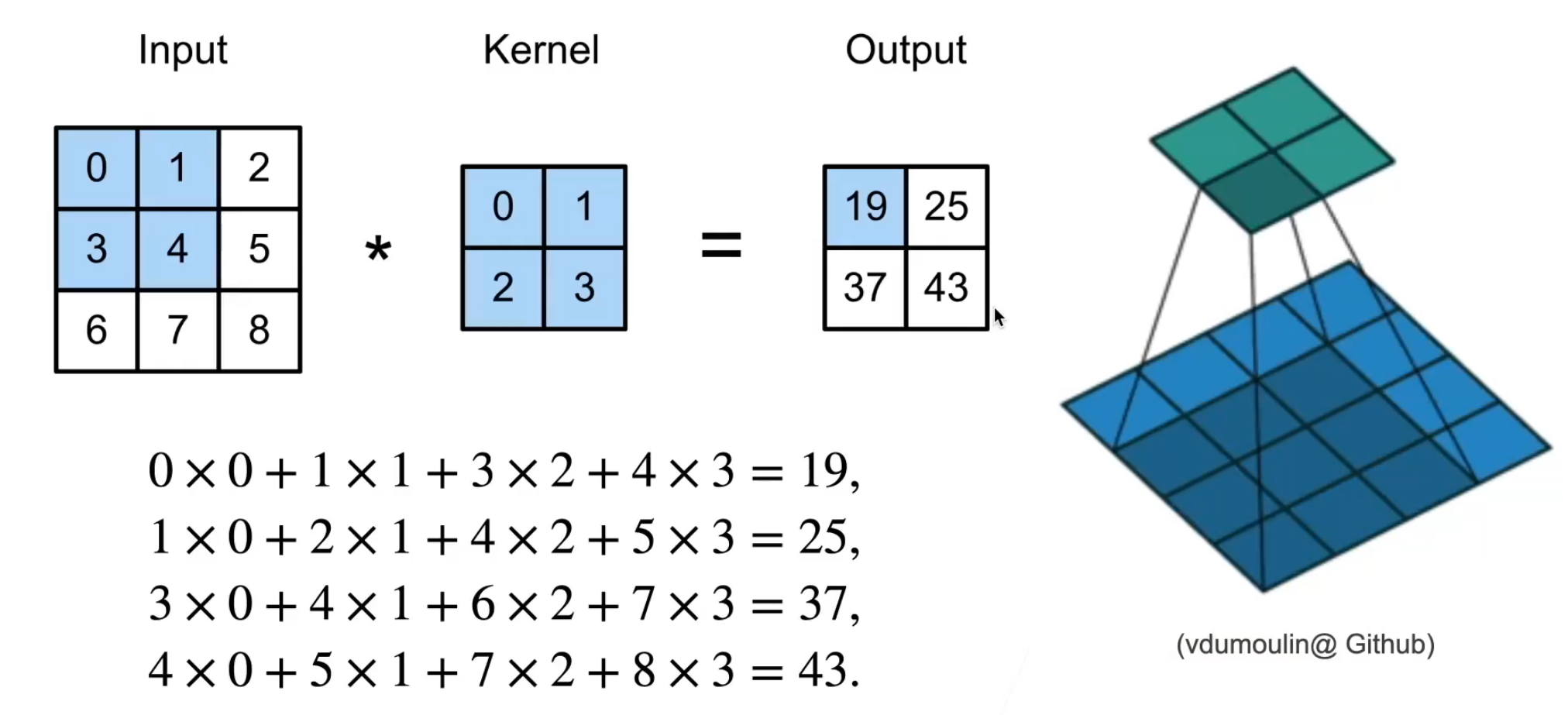
2D卷积需要4个嵌套循环4-double loop,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5。而且,对于滤波器,也有一定的规则要求:
1)滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2。
2)滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。
3)如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
4)对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
锐化滤波的核心规律是通过 "放大当前像素与周围像素的差异" 来增强图像细节和边缘,其滤波器设计、运算逻辑和效果原理可以拆解为以下几点:
1. 锐化滤波器的权重结构规律
锐化滤波器的权重分布有一个典型特点:
- 中间像素权重极大 :滤波器中心位置的权重是大的正数 (比如第一个 3×3 核的
5、带 k 的核的8k+1),且这个权重会大于周围所有权重的绝对值之和(保证原像素的基础信息不丢失); - 周围像素权重为负 / 小值 :滤波器周围位置的权重是负数(或较小的正数)
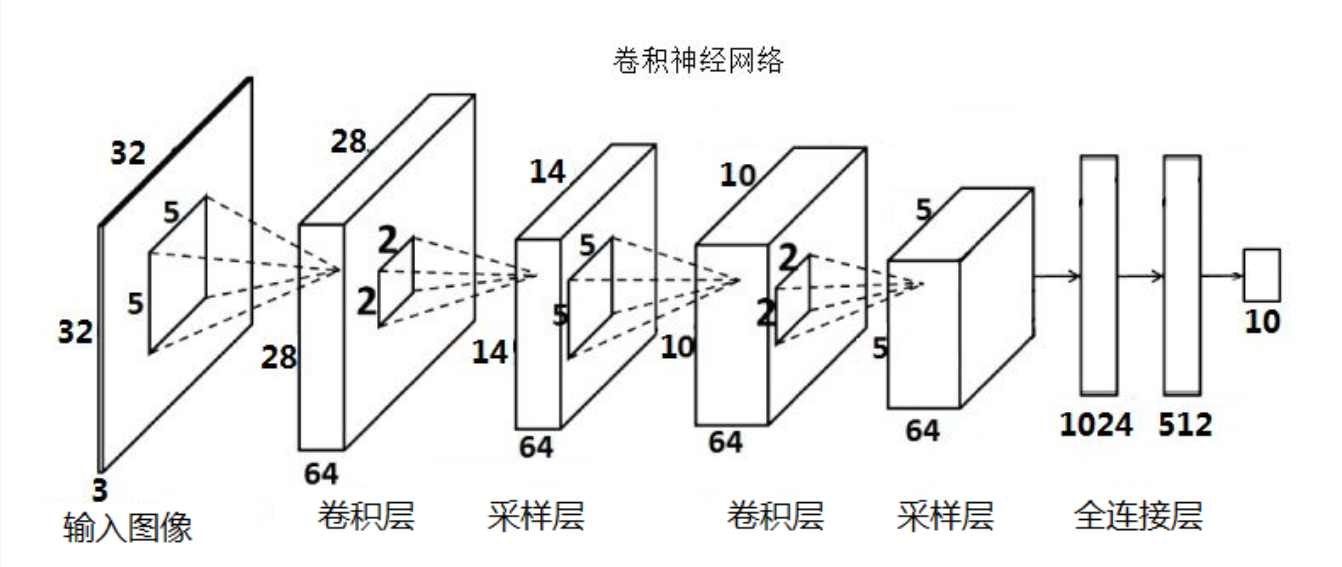
- 通过第一个卷积层提取最初特征,输出特征图(feature map)
- 通过第一个采样层对最初的特征图(feature map )进行特征选
- 择,去除多余特征,重构新的特征图
- 第二个卷积层是对上一层的采样层的输出特征图(feature map)进行二次特征提取
- 第二个采样层也对上层输出进行二次特征选择
- 全连接层就是根据得到的特征进行分类
CNN结构:
首先结构是:输入图像------全连接层
但是我们发现图像我们只要处理边缘特征就可以了不需要关注那么多的局部特征(比如识别数字,我们只要识别黑色数字就可以了不需要看灰色的区域,所以我们加入了采样层,只保留我们想要的。
结构变成了: 输入图像------采样层------全连接层
但是我们又发现这样参数还是太多了,我们需要对原始输入进行降维或者减少参数
卷积的运算
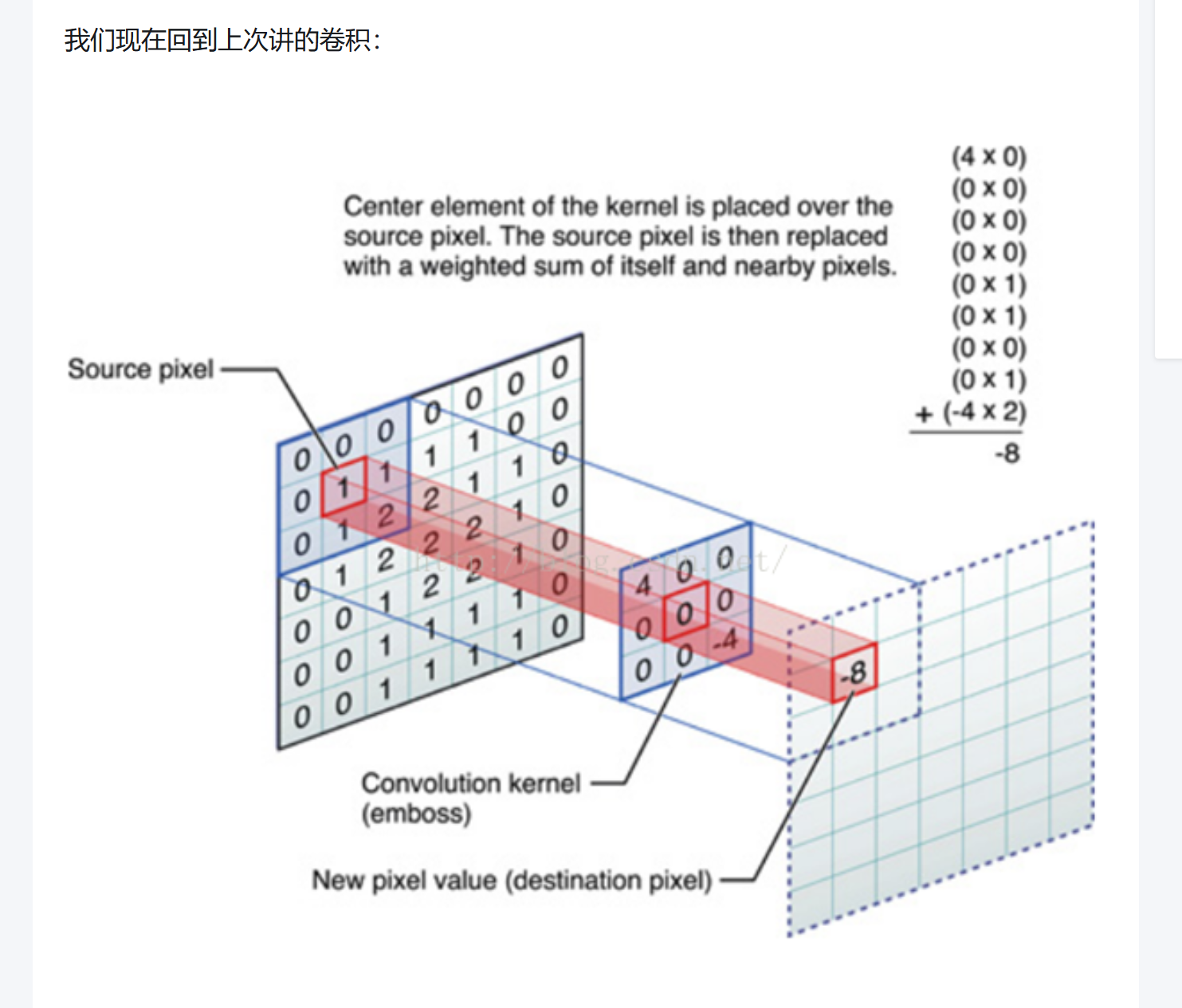
1. 第一步:卷积核与源像素对齐
卷积核(这里是 3×3 的 "浮雕核")的中心元素,要与输入图像中的 "源像素"(即当前要计算的区域中心像素)对齐,让卷积核刚好覆盖输入图像的一个局部区域。
比如图中:
- 输入图像的 "源像素" 是红色框标注的
1; - 3×3 卷积核的中间位置(第二行第二列) ,会与这个
1对齐,使卷积核覆盖1及其周围的像素区域。
2. 第二步:逐元素相乘
将卷积核的每个元素,和它覆盖的输入图像对应位置的元素,两两相乘。
以图中的计算为例(卷积核数值为:第一行[4, 0, 0]、第二行[0, 0, -4]、第三行[0, 0, 0]):
- 卷积核的
4对应输入区域的0→ 计算4 × 0; - 卷积核的多个
0,对应输入区域的0或1→ 计算0 × 0、0 × 1(这些项的结果都是 0); - 卷积核的
-4对应输入区域的2→ 计算-4 × 2。
3. 第三步:求和得到输出像素
把所有 "逐元素相乘" 的结果加起来,总和就是当前位置的 ** 目标像素(输出像素)** 值。
图中的计算总和为:4×0+(0×0)×n+(0×1)×m+(−4×2)=0+0+0−8=−8这个-8就是当前位置的输出像素值(图中红色框标注的 "New pixel value")。
卷积运算的核心规律总结
卷积(互相关)的通用运算步骤是:
- 滑动对齐:卷积核在输入图像上逐个位置滑动,每次将核的中心(或左上角,依定义)与输入的一个位置对齐,覆盖局部区域;
- 对应相乘:核的每个元素与覆盖区域的对应像素相乘;
- 累加输出:所有乘积的和,作为该位置的输出像素值。
在实际的图像处理中这个卷积核是训练出来的不是认为给定的
卷积核放在神经网络里,就代表对应的权重(weight)
卷积核里面的数字即相当于权重,卷积核里面的权值是怎么来的,后面我会在反向传播算法(backpropagation)中讲到
假设我们已经知道对应分量以及卷积核
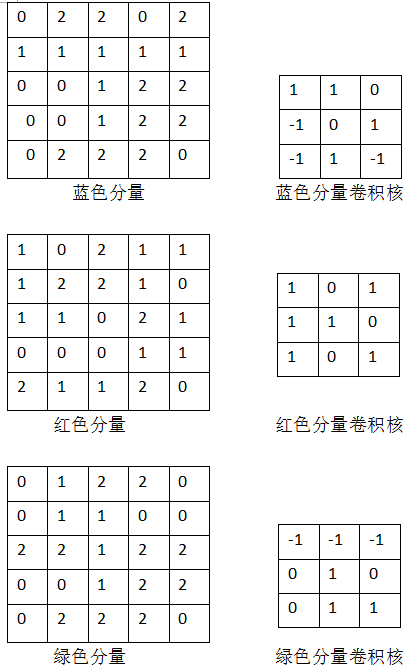
一、空间维度(高 / 宽)的关联
卷积层的输入空间尺寸(比如图像的高 Hin、宽 Win)、卷积核尺寸(k×k),再结合「步幅(s)」「填充(p)」,共同决定输出的空间尺寸(Hout、Wout)。
核心公式:
Hout=⌊sHin−k+2p⌋+1Wout=⌊sWin−k+2p⌋+1
其中:
- k:卷积核的边长(比如 3×3 的核,k=3);
- s:步幅(卷积核每次滑动的像素数,默认是 1);
- p:填充(在输入边缘补 0 的层数,默认是 0);
- ⌊⋅⌋:向下取整(保证尺寸为整数)。
例子
假设输入是一张 5×5 的图像(Hin=Win=5),用 3×3 的锐化核(k=3),步幅 s=1、无填充(p=0):Hout=15−3+0+1=3Wout=15−3+0+1=3输出尺寸就是 3×3(输入缩小了 "核边长 - 1" 的尺寸)。
二、通道维度的关联

卷积层的输入通道数(Cin)、输出通道数(Cout),与卷积核的通道数、数量直接相关:
- 卷积核的通道数 :必须与输入通道数 Cin 一致(比如输入是 RGB 图像,Cin=3,则每个卷积核也得是 3 通道的,才能覆盖所有输入通道);
- 输出通道数 Cout :等于卷积核的数量(每个卷积核会输出一个独立的通道,比如用 10 个 3×3 的核,输出通道数就是 10)。
例子:
输入是 (Cin=3,Hin=5,Win=5) 的 RGB 图像,用 2 个 (Cin=3,k=3,k=3) 的锐化核:
- 输出通道数 Cout=2;
- 输出空间尺寸 Hout=Wout=3;
- 最终输出尺寸是 (Cout=2,Hout=3,Wout=3)。
三、关键参数的影响
- 卷积核尺寸 k:核越大,输入尺寸缩小越多(无填充时,输出缩小 k−1 个像素);
- 填充 p:可以 "补偿" 尺寸缩小(比如 k=3 时,p=1 可让输出尺寸与输入一致);
我们称之为补0(zero padding)
因为添了一圈0,实际上什么信息也没有添,但是
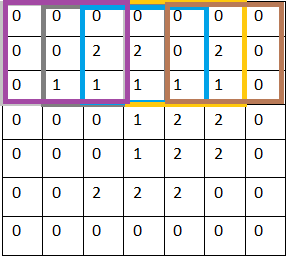
同样是stride x=1 的情况下,补0比原来没有添0 的情况下进行卷积,从左到右,从上到下都多赚了2次卷积,这样第一层卷积层输出的特征图(feature map)仍然为5x5,和输入图片的大小一致
而没有添0的第一层卷积层输出特征图大小为3x3
这样有什么好处呢
(1)我们获得的更多更细致的特征信息,上面那个例子我们就可以获得更多的图像边缘信息
(2)我们可以控制卷积层输出的特征图的size,从而可以达到控制网络结构的作用,还是以上面的例子,如果没有做zero-padding以及第二层卷积层的卷积核仍然是3x3, 那么第二层卷积层输出的特征图就是1x1,CNN的特征提取就这么结束了。
同样的情况下加了zero-padding的第二层卷积层输出特征图仍然为5x5,这样我们可以再增加一层卷积层提取更深层次的特征
- 步幅 s:步幅越大,输出尺寸越小(比如 s=2 时,输出尺寸会减半)。