LeetCode 3027.人员站位的方案数 II：简单一个排序O(n^2)——ASCII图解

【LetMeFly】3027.人员站位的方案数 II：简单一个排序O(n^2)------ASCII图解

力扣题目链接：https://leetcode.cn/problems/find-the-number-of-ways-to-place-people-ii/

给你一个 n x 2 的二维数组 points ，它表示二维平面上的一些点坐标，其中 points[i] = [x_i, y_i] 。

我们定义 x 轴的正方向为右（x 轴递增的方向 ），x 轴的负方向为左（x 轴递减的方向 ）。类似的，我们定义 y 轴的正方向为上（y 轴递增的方向 ），y 轴的负方向为下（y 轴递减的方向）。

你需要安排这 n 个人的站位，这 n 个人中包括 Alice 和 Bob 。你需要确保每个点处恰好有一个人。同时，Alice 想跟 Bob 单独玩耍，所以 Alice 会以 Alice的坐标为 左上角 ，Bob 的坐标为 右下角 建立一个矩形的围栏（注意，围栏可能不包含任何区域，也就是说围栏可能是一条线段）。如果围栏的内部或者边缘上有任何其他人，Alice 都会难过。

请你在确保 Alice 不会难过的前提下，返回 Alice 和 Bob 可以选择的点对数目。

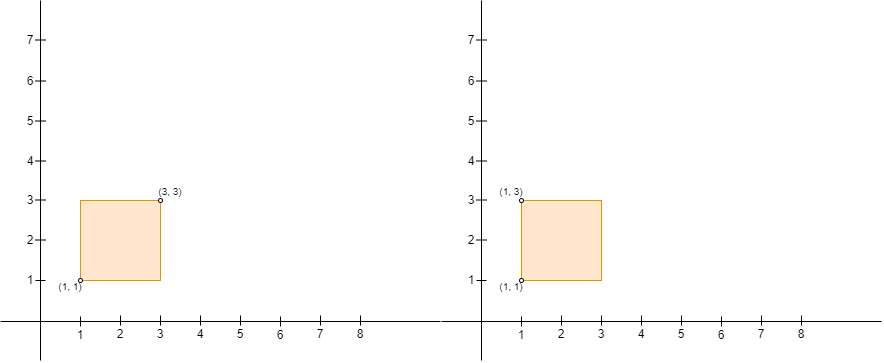
注意，Alice 建立的围栏必须确保 Alice 的位置是矩形的左上角，Bob 的位置是矩形的右下角。比方说，以 (1, 1) ，(1, 3) ，(3, 1) 和 (3, 3) 为矩形的四个角，给定下图的两个输入，Alice 都不能建立围栏，原因如下：

图一中，Alice 在 (3, 3) 且 Bob 在 (1, 1) ，Alice 的位置不是左上角且 Bob 的位置不是右下角。
图二中，Alice 在 (1, 3) 且 Bob 在 (1, 1) ，Bob 的位置不是在围栏的右下角。

示例 1：

复制代码

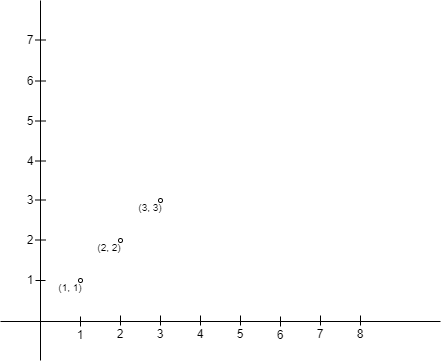
输入：points = [[1,1],[2,2],[3,3]]
输出：0
解释：没有办法可以让 Alice 的围栏以 Alice 的位置为左上角且 Bob 的位置为右下角。所以我们返回 0 。

示例 2：

复制代码

输入：points = [[6,2],[4,4],[2,6]]
输出：2
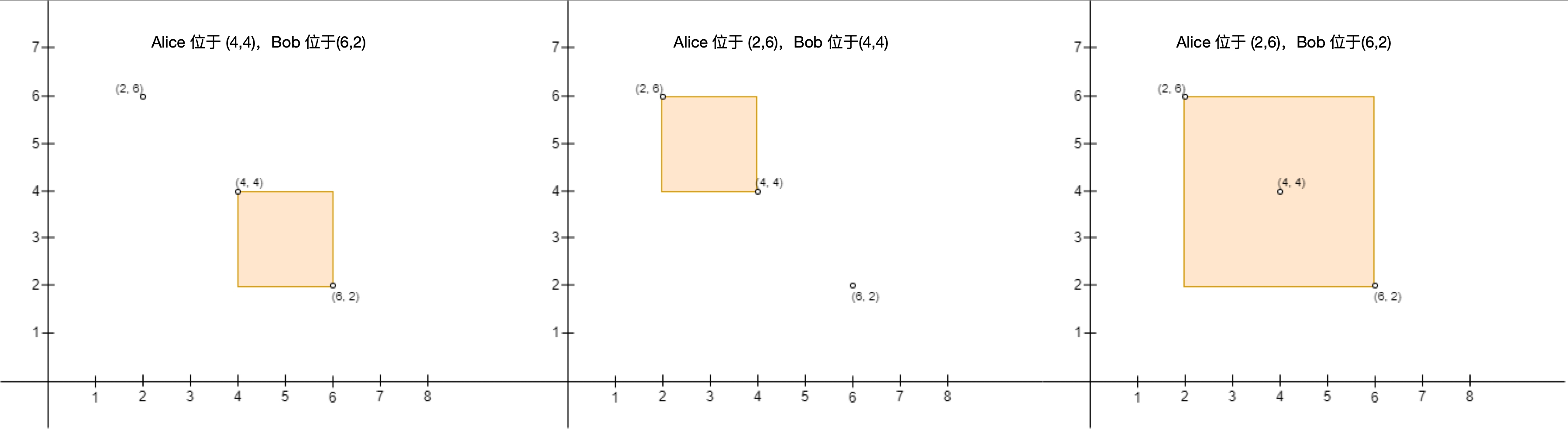
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (4, 4) ，Bob 站在 (6, 2) 。
- Alice 站在 (2, 6) ，Bob 站在 (4, 4) 。
不能安排 Alice 站在 (2, 6) 且 Bob 站在 (6, 2) ，因为站在 (4, 4) 的人处于围栏内。

示例 3：

复制代码

输入：points = [[3,1],[1,3],[1,1]]
输出：2
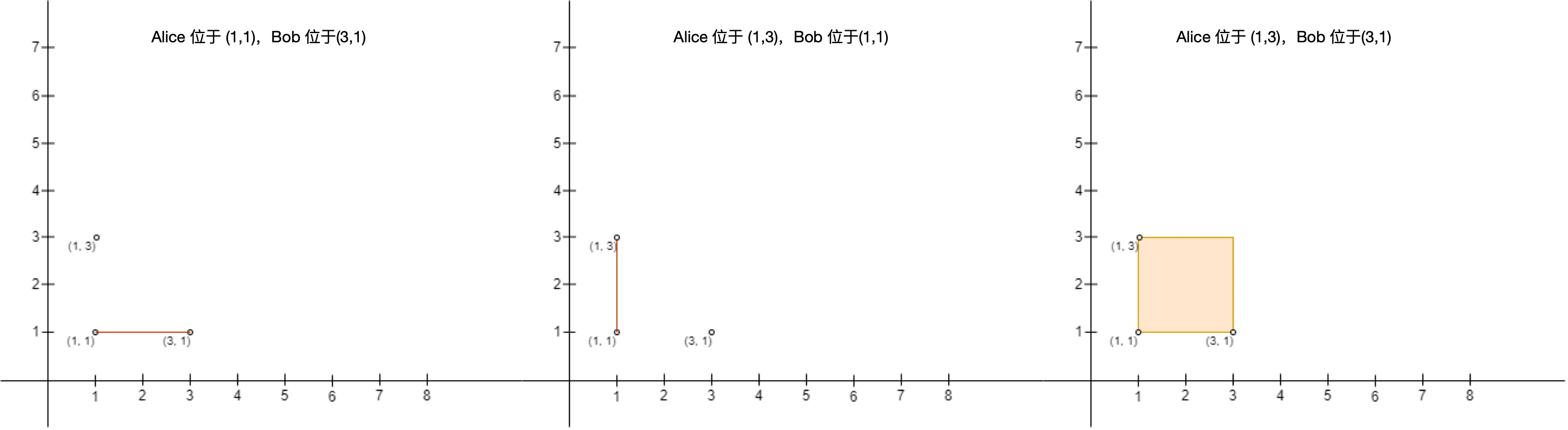
解释：总共有 2 种方案安排 Alice 和 Bob 的位置，使得 Alice 不会难过：
- Alice 站在 (1, 1) ，Bob 站在 (3, 1) 。
- Alice 站在 (1, 3) ，Bob 站在 (1, 1) 。
不能安排 Alice 站在 (1, 3) 且 Bob 站在 (3, 1) ，因为站在 (1, 1) 的人处于围栏内。
注意围栏是可以不包含任何面积的，上图中第一和第二个围栏都是合法的。

提示：

2 <= n <= 1000
points[i].length == 2
-10⁹ <= points[i][0], points[i][1] <= 10⁹
points[i] 点对两两不同。

解题方法：排序

数据范围是 1 0 3 10^3 103，因此可以二重循环：第一层循环枚举左上角的Alice，第二层循环枚举右下角的Bob，如果可以在O(1)时间内判断出Alice和Bob之间有无第三者，问题就解决了。

很容易想到排个序，最左边为最优先，最上边为次优先。

那么，对于一个Alice，在遍历Bob时，我们只需要使用一个变量mxY记录遍历过的合法Bob中最上边的那个。

复制代码

↑
|           * Bob4
|
|  * Alice
|              *Bob3
|
| - - - * - - - - - - - - mxY
|      Bob1
|
|           * Bob2
|
+---------------------------→
         ↑
     当前遍历到

例如合法的Bob1会把mxY提高到他的高度，后续所有Bob中（一定在Bob1的右下方），只要低于mxY（如Bob2），那么他和Alice之间一定会存在其他Bob；相反，只要后续Bob高于mxY且不低于Alice（如Bob3），那么他和Alice之间一定没有其他Bob（因为他左边的所有不高于Alice的Bob都比他低）。

而可怜的Bob4，由于他太高了，一定不会处在Alice的下方，不在此Alice的考虑范围内，不参与更新mxY。

别怕，代码很简单，一看就懂了。

时间复杂度 O ( n 2 ) O(n^2) O(n2)
空间复杂度 O ( log ⁡ n ) O(\log n) O(logn)，空间复杂度来自排序

OMG，一个Alice要面试好多个Bob(bushi)

AC代码

Python

python 复制代码

'''
Author: LetMeFly
Date: 2025-09-05 09:55:20
LastEditors: LetMeFly.xyz
LastEditTime: 2025-09-05 10:35:32
'''
from typing import List

class Solution:
    def numberOfPairs(self, points: List[List[int]]) -> int:
        points.sort(key=lambda x: (x[0], -x[1]))
        ans = 0
        for i in range(len(points)):
            mxY = -1000000001
            for j in range(i + 1, len(points)):
                if mxY < points[j][1] <= points[i][1]:
                    mxY = points[j][1]
                    ans += 1
        return ans

Python放前面是因为这次Python更便于理解。

C++

cpp 复制代码

/*
 * @Author: LetMeFly
 * @Date: 2025-09-05 09:55:20
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-09-05 10:05:44
 */
class Solution {
public:
    int numberOfPairs(vector<vector<int>>& points) {
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            return a[0] == b[0] ? a[1] > b[1] : a[0] < b[0];
        });
        int ans = 0;
        for (int i = 0; i < points.size(); i++) {
            int mxY = -1000000001;
            for (int j = i + 1; j < points.size(); j++) {
                if (points[j][1] > mxY && points[j][1] <= points[i][1]) {
                    ans++;
                    mxY = points[j][1];
                }
            }
        }
        return ans;
    }
};

Java

java 复制代码

/*
 * @Author: LetMeFly
 * @Date: 2025-09-05 09:55:20
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-09-05 10:44:46
 */
import java.util.Arrays;

class Solution {
    public int numberOfPairs(int[][] points) {
        Arrays.sort(points, (a, b) -> a[0] == b[0] ? b[1] - a[1] : a[0] - b[0]);
        int ans = 0;
        for (int i = 0; i < points.length; i++) {
            int mxY = -1000000001;
            for (int j = i + 1; j < points.length; j++) {
                if (points[j][1] > mxY && points[j][1] <= points[i][1]) {
                    mxY = points[j][1];
                    ans++;
                }
            }
        }
        return ans;
    }
}

Go

go 复制代码

/*
 * @Author: LetMeFly
 * @Date: 2025-09-05 09:55:20
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-09-05 10:40:12
 */
package main

import "sort"

func numberOfPairs(points [][]int) (ans int) {
    sort.Slice(points, func(i int, j int) bool {
        if points[i][0] == points[j][0] {
            return points[i][1] > points[j][1]
        }
        return points[i][0] < points[j][0]
    })
    for i := range points {
        mxY := -1000000001
        for j := i + 1; j < len(points); j++ {
            if points[j][1] > mxY && points[j][1] <= points[i][1] {
                mxY = points[j][1]
                ans++
            }
        }
    }
    return
}

Rust

rust 复制代码

/*
 * @Author: LetMeFly
 * @Date: 2025-09-05 09:55:20
 * @LastEditors: LetMeFly.xyz
 * @LastEditTime: 2025-09-05 10:49:59
 */
impl Solution {
    pub fn number_of_pairs(mut points: Vec<Vec<i32>>) -> i32 {  // 想原地sort points的话记得在points前面加上mut
        points.sort_by(|a, b| {
            if a[0] == b[0] {
                b[1].cmp(&a[1])
            } else {
                a[0].cmp(&b[0])
            }
        });
        let mut ans: i32 = 0;
        for i in 0..points.len() {
            let mut mx_y: i32 = -1000000001;
            for j in (i+1)..points.len() {
                if points[j][1] > mx_y && points[j][1] <= points[i][1] {
                    mx_y = points[j][1];
                    ans += 1;
                }
            }
        }
        ans
    }
}

同步发文于CSDN和我的个人博客，原创不易，转载经作者同意后请附上原文链接哦~

千篇源码题解已开源