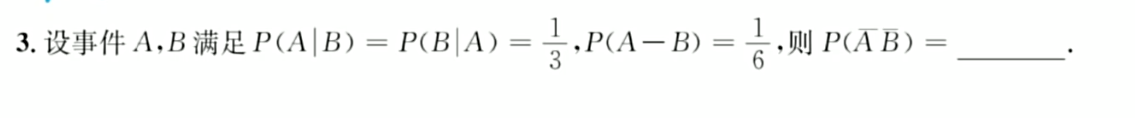文章目录
考纲

术语
- (随机)试验
- 随机事件
- 必然事件
- 不可能事件
- 样本点
- 样本空间
- 基本事件
- 完备事件组
- 概率
- 全集分解法
- 事件的独立性
- 独立试验序列概型
- n重伯努利概型
事件的关系与运算
事件的关系、运算与集合的关系、运算相当,且具有相同的运算法则,所以实在不会时可以考虑用文氏图来做。
关系
- 包含
- 相等
- 积(交)事件
- 相容
- 互斥
- 和(并)事件
- 差事件
- 逆(对立)事件
运算
- 吸收律
- 交换律
- 结合律
- 分配律
- 对偶律(德 ⋅ \cdot ⋅摩根律)
事件运算顺序约定为先进行逆运算,然后进行交运算,最后进行并或差运算。
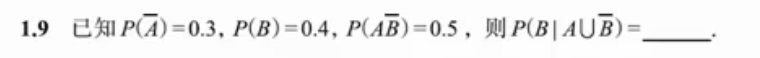
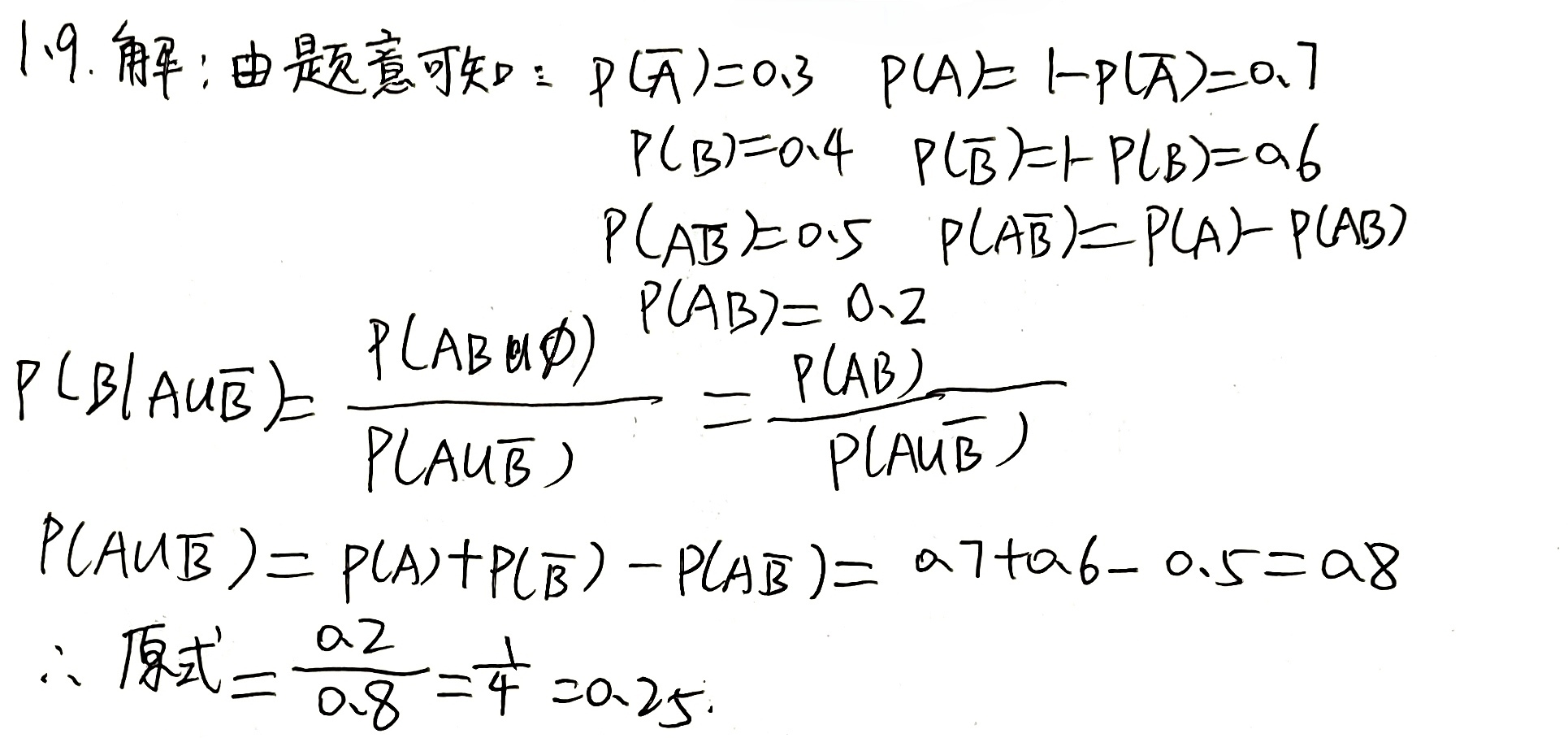
古典概型
概念和性质
如果随机试验的样本空间满足:
- 只有有限个样本点(基本事件)
- 每个样本点(基本事件)发生的可能性都一样
则称随机试验的概率模型为古典模型 ,事件A的古典概率计算公式:
P ( A ) = 事件 A 所包含基本事件的个数 基本事件总数 P(A) = \frac{事件A所包含基本事件的个数}{基本事件总数} P(A)=基本事件总数事件A所包含基本事件的个数
另外这里面可能会用到排列与组合的公式。
放入问题------随机分配
取出问题------简单随机抽样问题
几何概型
简而言之,基本事件无限且具有几何度量、等可能发生的随机试验为几何概型 。A的几何概率为:
P ( A ) = A 的几何度量 Ω 的几何度量 P(A) = \frac{A的几何度量}{\Omega的几何度量} P(A)=Ω的几何度量A的几何度量
常见的几何度量为面积或者体积,比如下面这道题:


一般的做题步骤就是先画图然后做计算。
概率的性质与计算
性质
有界性 :对于任一事件A,有 0 ≤ P ( A ) ≤ 1 0≤P(A)≤1 0≤P(A)≤1,且 P ( ∅ ) = 0 P(\varnothing) = 0 P(∅)=0
Ω 表示一个人在8点到9点之间进入教室的所有可能时间。这是一个连续的时间区间(例如,从8:00到9:00),因此 Ω 是一个连续样本空间。
事件 A 表示"恰好8:30到达教室"。**在连续概率分布中,任何单个时间点的概率都为零。**这是因为概率是通过积分计算的:概率密度函数在单个点上的积分为零。
**例如,如果到达时间均匀分布在8点到9点之间,那么概率密度函数是常数(f(t) = 1/60,其中 t 是以分钟计的时间)即使事件 A 可能发生(理论上有人可能正好在8:30到达),但其概率为零。**这类似于在一条线上选一个点,选到特定点的概率为零。
两个重要结论:
- P ( A ) = 0 ≠ > A = ∅ P(A)=0 ≠> A=\varnothing P(A)=0=>A=∅: **概率为0的事件不一定是不可能事件。**它只是意味着该事件发生的"机会"或"测度"为0,但在无限多的可能性中,它仍然可能发生。
- P ( A ) = 1 ≠ > A = Ω P(A)=1 ≠> A=Ω P(A)=1=>A=Ω: **概率为1的事件不一定是必然事件。**它意味着该事件"几乎肯定"会发生,但样本空间中可能存在一些"例外点",这些点的集合的测度为0。
比如:几何概率 - 在平面上随机选一个点
样本空间 Ω: 单位正方形 [0,1]×[0,1] 内的所有点
- 事件 A: "点恰好落在对角线 y=x 上"。
分析: 对角线是一条没有宽度的"线"。它的面积(2维测度)为0。因此,随机扔一个点恰好落在这条线上的概率 P(A) = 0。
结论: P(A)=0 ,但A 显然不是空集,因为对角线上有无限多个点(例如(0,0), (0.5,0.5), (1,1)等都是可能的结果)。 - 事件 B: "点没有落在对角线 y=x 上"。
分析: P(B) = 1 - P(A) = 1。
结论: P(B)=1,但 B 不等于整个样本空间 Ω,因为它排除了对角线上的所有点。
计算
-
加法公式
-
减法公式
-
逆事件概率公式
-
条件概率公式
-
乘法公式

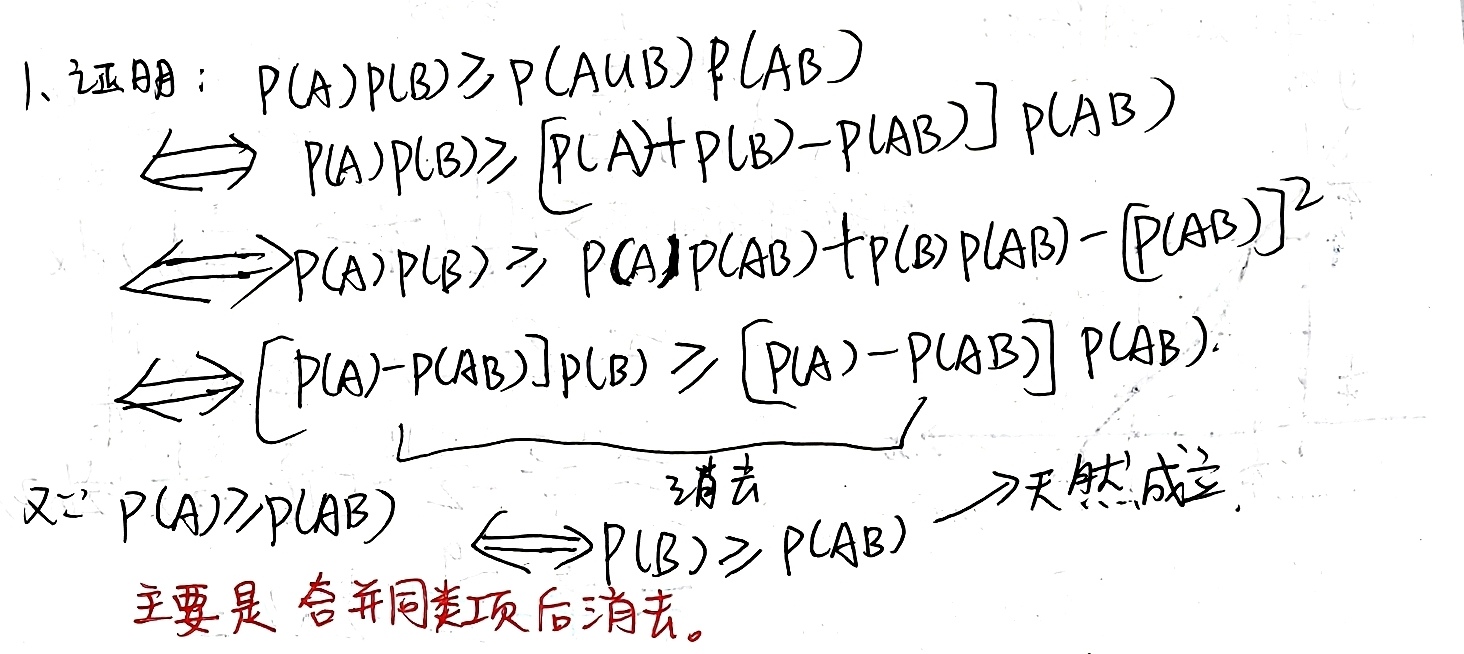
做证明题还要有举反例的思路,反例可以是特殊值,比如令P(AB)=0等。
-
全概率公式


-
贝叶斯公式(逆概率公式)

事件的独立性和独立的判定
事件的独立性
设A,B为两个事件,如果 P ( A B ) = P ( A ) P ( B ) P(AB)=P(A)P(B) P(AB)=P(A)P(B),则称事件A与B相互独立,简称A与B独立。
判定定理

举反例的思想

独立试验序列概型与n重伯努利概型
在第二讲中会进一步看到应用,如果用X表示n重伯努利概型中事件A发生的次数,则X服从二项分布B(n,p)
错题
如果简单的题做错,那么真正在考场上的时候怎么办?