在焊接、装配、喷漆、施工和物体擦作等机器人应用中,机械臂被编程为在共享工作空间中执行许多任务。为了减少整体执行时间并提高吞吐量,可以将更多机器人放置在同一个单元中以同时执行任务。与复制整个机床相比,这种高密度设置有可能减少执行时间,同时将成本和空间的增加降至最低。
然而,在密闭空间内高效协调多个机器人在理论和技术上都存在困难,因为规划者必须共同解决任务分配、调度和无碰撞运动规划问题,所有这些问题都具有很高的组合复杂性,通常在具有复杂障碍物几何形状的环境中。这项工作在多个机器人可以按任何顺序执行所有任务的环境中解决了这一挑战,这代表了搜索空间大小方面最具挑战性的场景。在关节空间中找到一条将机器人末端执行器移动到位姿目标的无碰撞路径是该问题的运动规划方面,并且通常使用基于采样的方法来解决,例如快速探索随机树 (RRT) 及其变体 。然而,尽管这些基于采样的算法旨在处理高维配置空间并提供概率完整性,但它们的运行时间在配置空间的维度和障碍的复杂性方面呈指数级增长。在实践中,当尝试同时使用所有机器人进行规划时,这些技术仅适用于相对较小的配置空间 [两个或更少的机器人]。一种潜在的解决方案是按顺序为每个机器人进行规划;然而,这种表述带来了自己的挑战,因为其他机器人必须被视为移动障碍物,而基于采样的运动规划器也难以解决,并且需要将其他机器人的路径转换为扫描体积等技术,然后过度限制规划器的搜索空间,并可能导致次优解决方案或规划失败。与路径规划问题类似,任务调度问题(决定任务的完成顺序)也是多项式空间(PSPACE)完整的,形式化为旅行推销员问题(TSP)。尽管TSP的精确解对于现实世界的问题大小在计算上是不可行的,但存在许多具有不同最优性/效率权衡的近似解。将这些解决方案应用于任务调度的主要挑战是,与其像经典制定的TSP那样在每对任务之间移动具有固定成本,而是可以根据其他机器人的轨迹修改从一个任务移动到另一个任务所需的关节空间轨迹,并且每个潜在轨迹都有不同的成本。此外,每个任务通常有多个逆运动学 (IK) 解决方案,要么是因为任务没有完全约束,要么是机器人的自由度 (DoF) 比任务多。对于七自由度的机械臂,每个六自由度的任务位姿有多达无限数量的 IK 解决方案。一个好的路径规划算法在选择用于解决每个任务的最佳 IK 解决方案时必须考虑整个任务序列。任务分配问题又增加了一层复杂性。找到一个最小化总执行时间的机器人任务分配在概念上类似于经典背包问题的多容器变体 ,只是我们不知道在不解决整个计划问题的情况下将额外任务分配给机器人的边际成本,成本也与机器人正在解决的其他任务无关。因此,背包问题的算法解决方案在这种情况下实际上没有帮助。由于每个子问题的渐近复杂度很高,因此将现有算法与完整性保证相结合以共同解决现实世界问题大小的高密度多机器人规划在计算上是不可行的,因为它们在机器人数量、任务数量和障碍物复杂性方面呈指数级扩展。相反,现有方法侧重于将问题分解为可管理的子问题,一次解决一个问题,通常是迭代的,以生成具有现实计算要求的解决方案。然而,这种方法为了计算可行性而牺牲了潜在的解决方案最优性,并且仍然无法扩展到实际应用的环境复杂性,因为目前最先进的技术报告通过在高级任务规划器和低级运动规划器之间迭代,仅可扩展到五个机器人和 10 个任务,并有一些基于可达性和可用性的启发式方法。行业目前依赖于手动轨迹规划和复杂的联锁时间表,以确保无碰撞运行。这些轨迹通常需要数百或数千小时来手动设计,对任务或环境的任何更改都需要耗时的手动重新规划。为了应对这一挑战,DeepMind 联合伦敦大学研究人员提出了 RoboBallet,这是一种基于启发式的学习方法,用于在随机生成的环境中进行任务和运动规划,能够在与训练期间看到的环境不同的环境中规划多臂到达轨迹,具有任意障碍物几何形状、任务姿势和机器人位置。任务和运动规划是一大类问题,需要高级离散调度和低级连续规划来解决。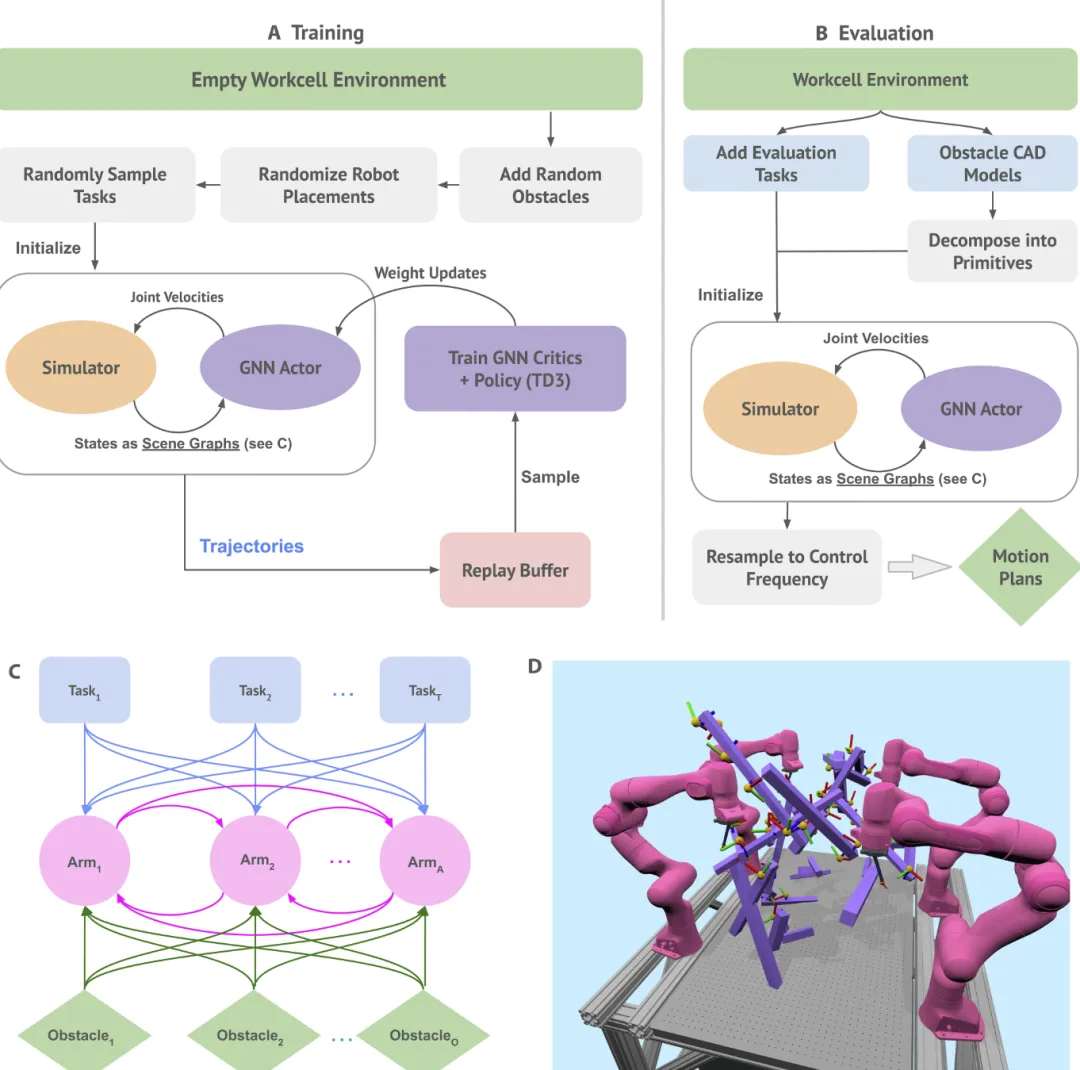
在这项工作中,为了简单起见,他们专注于 reaching 子类。具体来说,他们解决了可扩展性和高效任务调度是主要挑战的问题,没有隐式或显式的任务相互依赖性,并且每个单独的任务都很容易完成。该方法共同解决了任务分配、调度和运动规划问题,没有现有方法中常见的手工设计的简化,例如预采样固定数量的IK解决方案,根据启发式方法将任务预分配给机器人,或一次为一个机器人规划子轨迹。我们的主要见解是采用深度强化学习(深度强化学习)方法,训练智能体在每个时间步长控制手臂。这将昂贵的在线计算转移到离线阶段,将计算需求从规划阶段摊销并转移到训练阶段,使需要在许多类似设置或具有许多变体的设置上规划解决方案的应用程序受益。通过支持的配置变化进行训练,例如机器人定位和形态、任务类型或障碍物类型,RoboBallet 可以在测试时快速生成针对各种环境和新配置的计划,而无需进一步训练。训练后,他们可以简单地在现实世界中执行这些控制器,或者,为了安全起见,他们可以通过使用前向运动学模拟器逐步展开策略来生成解决方案轨迹,以便可以对其进行检查并可能进一步处理。然而,深度 RL 在多臂任务和运动规划中的朴素应用也无法扩展到琐碎的场景之外,因为场景复杂性仍然按组合方式扩展,这会导致代表代理策略的底层深度神经网络所需大小呈指数级扩展。这项工作的主要贡献是使用图来表示状态,以及使用图神经网络(GNN)进行RL策略和状态行动价值估计。GNN使用权重共享来允许缩放图大小而不缩放模型复杂性,类似于卷积神经网络(CNN)具有独立于图像大小的固定内核大小,并且推理时间复杂度在机器人数量上是二次的------有关更多详细信息,请参阅讨论部分。状态图的构造使得图节点表示机器人、障碍物和任务,图边将每个任务和每个障碍物连接到每个机器人,每个机器人相互连接,支持机器人之间的协调,并允许每个节点接收足够的环境信息,以规划一条无冲突的任务路径(图1)。图1.训练和评估路径。(A) 训练路径。每一集都从一个空表开始,在上面添加随机长方体障碍物,随机放置机器人,并随机抽样末端执行器任务。GNN Actor 与运动学模拟器交互以尝试完成任务。轨迹存储在重放缓冲区中,并用于使用 TD3 训练批评者和策略函数。(B)评估路径,其中外部定义的任务与障碍物一起分解为碰撞原语,用于构建模拟环境,GNN以与训练相同的方式与该环境进行交互。(C)场景图的地形图,包含机器人、任务和障碍物节点,机器人之间的双向边和每个任务的单向边以及每个机器人的障碍物原语。(D) 简化训练单元,减少障碍和任务的数量。每个任务都被指定并可视化为机器人末端执行器必须匹配的坐标系,其中蓝色/z 轴与末端执行器的径向轴对齐。
通过这种公式,RoboBallet 可以直接同时控制多个(这里最多八个)七自由度机器人,协调多达 56 维的配置空间,并处理多达 40 个共享任务,机器人分配和任务调度完全不受限制。该模型在每个 100 毫秒的时间步长中确定所有机器人中所有关节的目标关节速度,我们的环境设置只需应用速度和加速度钳位,阻止机器人碰撞,并整合生成的速度以生成关节配置航点。RoboBallet 采用了一种优先考虑可扩展性的方法,并权衡理论保证,以便在更大规模的问题上实现实际部署(在密集环境中使用多达八个机器人进行测试),同时展示经验高质量的解决方案。RoboBallet 为许多工业应用开辟了令人兴奋的可能性,例如工作单元布局优化、在一台机器人发生故障时快速重新规划,以及使用基于图像的姿态估计来处理工件位姿的运行变化,以捕捉规划人员的工件姿势,以及使用相机或 LIDAR(光检测和测距)系统进行三维 (3D) 环境重建的环境变化。RoboBallet 是一项使能技术,它为这些重要功能打开了大门,而这些功能迄今为止由于多机器人制造环境中手动任务和运动规划的高成本和延迟而无法实现。