配套视频课程 www.bilibili.com/video/BV1Rx...
【机器学习与实战】回归分析与预测-线性回归-03-损失函数与梯度下降
四、损失函数
根据上述数据集的相关性分析，目前我们来确定一个模型类型：y=wx+b，最简单的一元线性回归模型。在模型没有被正式确定之前，我们只能称该函数为假设函数（可以使用y'来表示，只是一个名称，不重要）。但是由于我们有160条数据样本，也就是说，机器学习时会有160个函数，比如会构造y1=5x+3，y2=58x+12......，那么此时，如何来评估哪一个函数更好呢？这就需要引入损失（loss）函数，也就是目标就是损失最小，如果模型完全准确，则损失为0。（极端情况，一般不可能达到0，最多无限接近于0）。某此地方通常用 j(θ) 或 L(w,b) 来表示损失函数，也就是说，损失函数不解决x和y的关系，只处理w和b这两个参数关系。
在计算损失函数时，由于只关心w和b两个参数，而不再关心x和y的值（此处x为微信广告费，y为销售额），原本x和y才是变量，但是在求解损失函数时，则将x和y看作定值（本来样本里面就有x和y），而将w和b看作变量。
机器学习的过程，就是动态不断调整w和b来使平均损失最小，而此时得到的w和b就是最优解。计算损失的函数有很多种，目前先了解线性回归模型最常用到的：均方误差函数来实现。
（1）对于每一个样本，其预测值和真实值之间的差异为(y'-y)，而y'=wx+b，所以损失值与参数w和b有关。
（2）如果将损失值（y'-y)夸张一下，进行平方运算（因为y'-y 有可能是负数），而平方后就可以变为正数，此时叫平方损失。
（3）然后，把所有样本的平方损失相加，再根据样本的数量求平均值，则得到一个损失函数为：
当然，也可以写成以下格式（为什么分母变成了2N呢，是因为如果要f(x)-y是2次方，求导出来的2正好可以和分母的2抵消）。当然，这个不是必须的，因为对于损失来说，多除以2或者不除以2，始终都是在找最小损失，对结果是没有影响的。另外，公式中
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> ( x , y ) ∈ D \large (x,y)\in D </math>(x,y)∈D
的这种表示方式代表x和y均属于数据集，与 i 从1到n更能表现公式的作用。
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> M S E = L ( w , b ) = 1 2 N Σ ( x , y ) ∈ D ( ( w x + b ) − y ) 2 \huge MSE = L(w,b) = \frac{1}{2N}\Sigma_{(x,y)\in D}((wx+b)-y)^2 </math>MSE=L(w,b)=2N1Σ(x,y)∈D((wx+b)−y)2
上图中，f(x)-y为就是预测值和真实值之间的差异，之所以平方，是为了计算绝对距离，否则大量的y-y'之和将可能导致分子为0，损失为0，显然这是不合理的，同时，只有使用平方，才能确保目标函数拥有最小值。其实公式本身里面有什么字母来表示不重要，重要的是弄清楚公式每一项所代表的意义，因为不同的文章作者，给出的公式的字母可能都不一样，不重要。利用Python代码实现上述公式如下：
ini
import pandas as pd
import numpy as np
# 均方差损失函数
def loss_function(x, y, w, b):
y_hat = w*x + b
loss = y_hat - y
cost = np.sum(loss**2)/len(x) # 也可以2*len(x)，损失最小，多除以2依然是最小，对结果没有影响
return cost
# 利用损失函数计算微信和销售额函数的损失
if __name__ == '__main__':
ads = pd.read_csv('./advertising.csv')
x = np.array(ads.wechat)
y = np.array(ads.sales)
loss_1 = loss_function(x, y, 5, 3)
loss_2 = loss_function(x, y, 58, 12)
print(loss_1, loss_2)输出结果为：
14886965.876199998 2016120207.37655损失相当巨大，所以说明y1=5x+3，y2=58x+12这两个函数都不是是优解，但是相对来说，y1=5x+3 比 y2=58x+12 更好一点。但是凭直觉感觉肯定不能用，其实我们也可以使用matplotlib来对参数5和3进行绘图，来感受一下是否可用：
matlab
# 前面的代码略，只需要x_train的数据来拟合出预测的Y和真实的Y值做比较就可以了
line_x = np.linspace(x_train.min(), x_train.max(), 500)
line_y = [5*xx+3 for xx in line_x]
plt.plot(line_x, line_y, 'b--')
plt.plot(x_train, y_train, 'r.') # 绘制训练集真实数据的散点图
plt.show()图像如下：
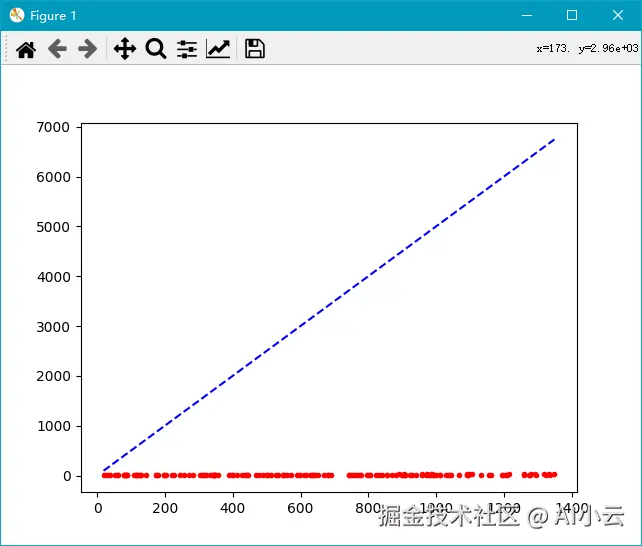
上述这张图的X和Y的坐标都很大，虽然也能看出来预测值和真实值之前完全没有相关性可言，也就是5x+3这个函数完全不可用。但是可读性还是很差，此时怎么办呢？我们需要对数据进行归一化处理即可，代码如下：
scss
x_train, x_test = scaler(x_train, x_test)
y_train, y_test = scaler(y_train, y_test)
loss_1 = loss_function(x_train, y_train, 5, 3)
loss_2 = loss_function(x_train, y_train, 58, 12)
print(loss_1, loss_2)
line_x = np.linspace(x_train.min(), x_train.max(), 500)
line_y = [5*xx+3 for xx in line_x]
plt.plot(line_x, line_y, 'b--')
plt.plot(x_train, y_train, 'r.') # 绘制训练集真实数据的散点图
plt.show()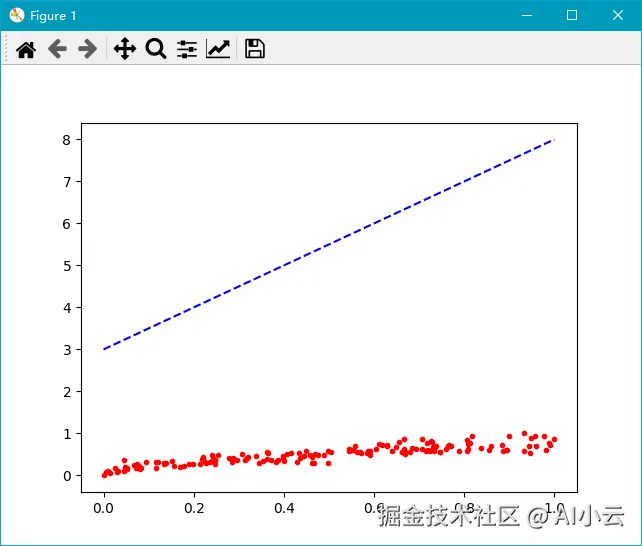
或者调整w参数为-5，得到如下图形：
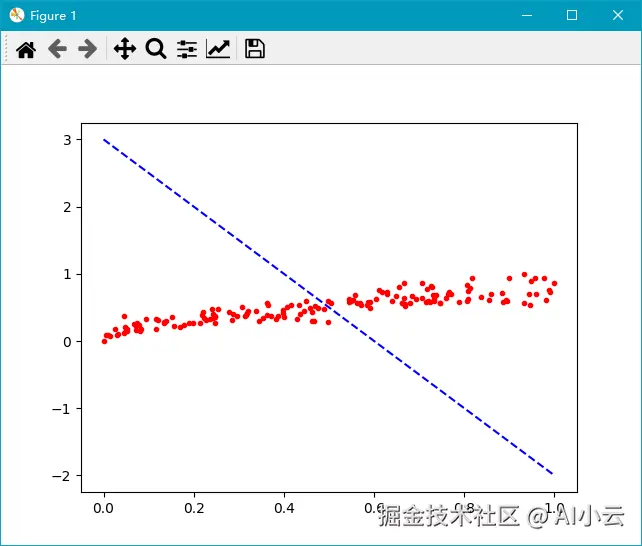
此时我们可以看到损失值也变小了：
yaml
25.592781941560116 1813.4234376624215以上图都可以非常直观地说明y=5x+b或y=-5x+b这两个函数是不可用的。那么如何寻找可用的参数组合呢？
在机器学习的训练过程中，就是每取得一组参数（w和b），就通过假设函数求y'，然后计算损失，记录下来并更新参数，形成一个新的假设函数，不断迭代，直到找到损失最小的那个参数，便构成了一个确定的函数。而此处有一个疑问，如何确定w和b的参数呢，其实这里就是一个非常关键的点，由于有损失函数帮助机器确定最优解，所以w和b的初始设置是什么不重要，迭代过程慢慢求解即可。
比如机器训练时，先随机生成10000组w和b的组合，然后不停计算损失值，这样的话，一定可以找到这10000个参数组合里面损失最小的那一个参数组合，对吗？但是这里有一个问题，这样求解的过程，只能得到这10000个组合里面的最优解，但是这大概率不是训练样本的最优解，否则就太随意了，怎么办呢？
五、梯度下降
梯度下降可以说是机器学习的精髓，各种机器学习所产生的奇迹，都必须建立在梯度下降的机制之下才有了让人感觉智能的结果。而之前讲的凸函数和最低点，则是梯度下降的关键，解决了两个问题：往哪个方向改变参数是正确的方向，在什么时候找到了最低点后就能够停止训练。
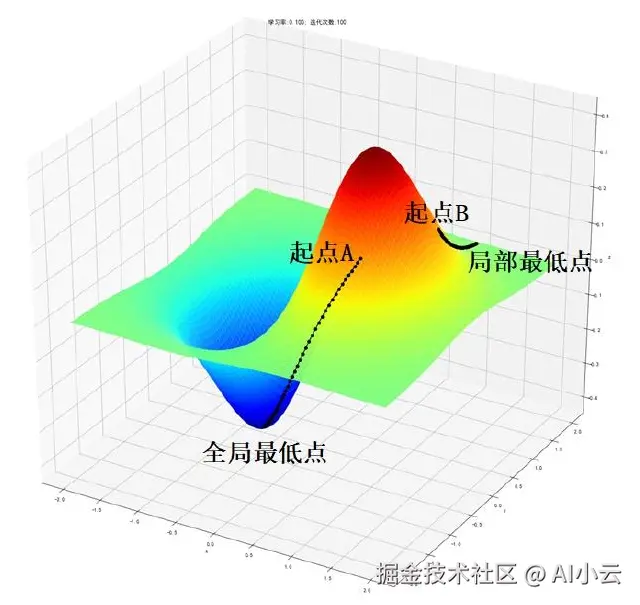假设对于参数w，给予一个初始权重，比如为10，那么根据下面的凸函数，下一次的权重应该设置为11还是9更合适呢？
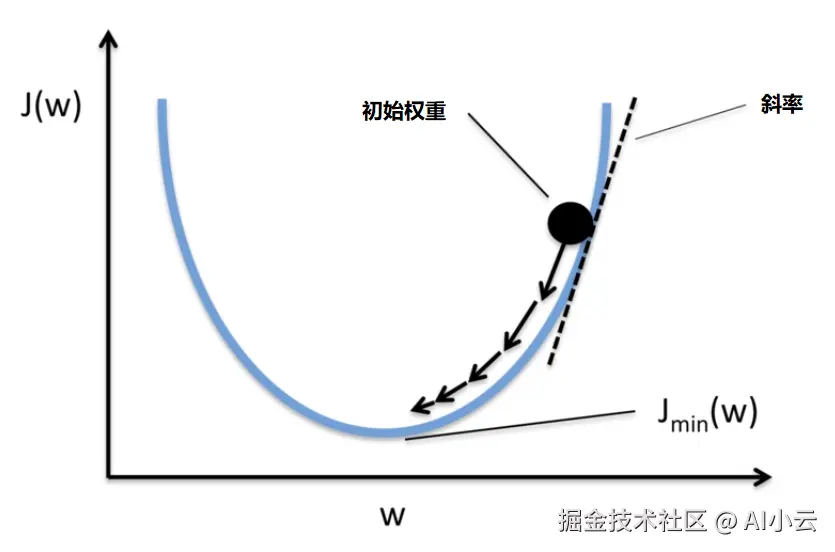
显然应该设置为9，才能够让权重w更倾向于损失最小的方向进行调整。而如何知道应该是9而不是11呢？这就依靠斜率的正负来确定方向，而具体是9还是9.9或者9.99，则由斜率的大小来确定权重w的调整幅度。
对于上节课的问题，有损失函数：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> C o s t = L ( w , b ) = 1 2 N Σ ( x , y ) ∈ D ( ( w x + b ) − y ) 2 \huge Cost = L(w,b) = \frac{1}{2N}\Sigma_{(x,y)\in D}((wx+b)-y)^2 </math>Cost=L(w,b)=2N1Σ(x,y)∈D((wx+b)−y)2
计算其梯度其实就是对上述公式进行求导，可以得出权重的梯度函数为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> 梯度 = δ δ ( w ) L ( w ) = δ δ ( w ) 1 2 N Σ ∗ ( x , y ) ∈ D ( ( w x − y ) 2 \huge 梯度 = \frac{\delta}{\delta(w)}L(w)=\frac{\delta}{\delta(w)} \frac{1}{2N} \Sigma*{(x,y)\in D}((wx-y)^2 </math>梯度=δ(w)δL(w)=δ(w)δ2N1Σ∗(x,y)∈D((wx−y)2
最终将公式简化为：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> 梯度 = 1 N Σ ∗ i = 1 N ( ( w ⋅ x i − y i ) ⋅ x i \huge 梯度 = \frac{1}{N} \Sigma*{i=1}^N((w\cdot x^i-y^i) \cdot x^i </math>梯度=N1Σ∗i=1N((w⋅xi−yi)⋅xi
上述公式使用Python代码实现如下：
ini
def gradient(x, y, w, b):
y_hat = w*x + b # 预测测试y
loss = y_hat - y # 损失
d_w = x.dot(loss)/len(x) # 实现(w*x-y)*x ，对w求导，注意x的形状，必要时可能需要x.T进行转置
d_b = sum(loss)*1/len(x) # 对b求导，*1的意思是把偏置看作w0，需要给x添加一行数字1，形成x0，保持偏置不变
print(d_w, d_b)
# 如果对偏置b的导数计算公式不清楚，也可以这样来写，保持跟w的公式一致：
b = np.ones(200)
d_b = b.dot(loss)/len(x) # 因为b的值均为1，所以点积与求和本质是一样的上述公式可以解决往哪个方向走的问题（也就是说下一次调整w参数的值应该是变小还是变大更能够获取更小损失值）的，如果求导后梯度为正值，则说明应该减少w，否则应该增加w。接下来还需要一个公式来解决学习速率的问题，也就是确定了w是变大和变小后，那到底变大和变小的幅度问题，公式如下：
<math xmlns="http://www.w3.org/1998/Math/MathML" display="block"> w = w − α ⋅ 梯度 = w − α N Σ i = 1 N ( ( w ⋅ x i − y i ) ⋅ x i \huge w=w-\alpha\cdot 梯度= w-\frac{\alpha}{N}\Sigma_{i=1}^N((w\cdot x^i-y^i) \cdot x^i </math>w=w−α⋅梯度=w−NαΣi=1N((w⋅xi−yi)⋅xi
利用Python求解梯度下降和学习速率的代码如下：
ini
import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
def gradient_descent(x, y, w, b):
y_hat = w*x + b
loss = y_hat - y
d_w = x.dot(loss) / len(x) # 求权重w的梯度（导数）
d_b = sum(loss) / len(x) # 求偏置b的梯度（导数）
return d_w, d_b
def learn_rate(w, b, l_r, d_w, d_b):
w = w - l_r * d_w
b = b - l_r * d_b
return w,b
def scaler(train, test):
min = train.min(axis=0)
max = train.max(axis=0)
gap = max - min
train -= min
train /= gap
test -= min
test /= gap
return train, test
if __name__ == '__main__':
ads = pd.read_csv('./advertising.csv')
x = np.array(ads.wechat)
y = np.array(ads.sales)
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
x_train, x_test = scaler(x_train, x_test)
y_train, y_test = scaler(y_train, y_test)
g_w_1, g_b_1 = gradient_descent(x_train, y_train, 5, 3)
g_w_2, g_b_2 = gradient_descent(x_train, y_train, 58, 12)
print(g_w_1, g_w_2)
print(g_b_1,g_b_2)
# 速率l_r也任意确定，比如1或者0.01
w_1, b_1 = learn_rate(5, 3, 1, g_w_1, g_b_1)
w_2, b_2 = learn_rate(58, 12, 1, g_w_2, g_b_2)
print(w_1, b_1)
print(w_2, b_2)输出结果为：
diff
5.408348332483047 47.06441311281033
4.900833097168485 39.243886616230085
-0.4083483324830466 -1.9008330971684853
10.935586887189672 -27.243886616230085这个结果过于魔幻，虽然我们是随机给定一组参数和学习速率，但是机器学习的过程就是基于我们给定的任意初始值进行迭代，逐步求解，所以一开始给的权重w，偏置b和学习速率alpha（l_r），是什么并不重要，如果你不知道如何给，可以全部赋值为1都是可以的。
上述过程g_w_1的值为5.408348332483047，或者w_1为-0.4083483324830466，这些数字并不代表具体某个意义，我们在计算梯度下降的过程中，更主要的是观察不同参数值对应的损失函数所计算出来的值，并关注其变化趋势即可。